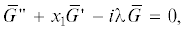Известия РАН. Энергетика, 2021, № 1, стр. 149-160
Аналитическое решение и функция Грина первой краевой задачи нестационарной теплопроводности в ограниченной области с границей, движущейся по корневой зависимости
Г. С. Кротов *
Академия труда и социальных отношений (АТИСО)
Москва, Россия
* E-mail: yamaths555@gmail.com
Поступила в редакцию 07.11.2020
После доработки 01.12.2020
Принята к публикации 04.12.2020
Аннотация
Развит метод функций Грина для уравнения нестационарной теплопроводности в ограниченной области с границей, движущейся по закону $\beta \sqrt t $. Метод приводит к точным аналитическим решениям краевых задач в условиях температурного нагрева. Получен явный вид функции Грина для первой краевой задачи в описанной выше области. Показана эквивалентность результатов, полученных с помощью метода функции Грина и другими методами.
Ключевые слова: функция Грина, первая краевая задача, нестационарная теплопроводность, уравнение теплопроводности, движущаяся граница, интегральное преобразование
ВВЕДЕНИЕ
Нахождение решений задач нестационарной теплопроводности имеет как практический, так и сугубо научный интерес. Например, это касается различных вопросов термоупругости, гидромеханики, фазовых превращений, процессов диффузии, абляции, горения [1], [2]. Несмотря на хорошо развитую аналитическую теорию нестационарного тепломассопереноса и близких направлений, достигнутые за последнее время успехи в нахождении точных аналитических решений весьма незначительны. Среди них можно отметить, например, работы [3] и [4], в которых получены функции Грина и точные аналитические решения задачи нестационарной теплопроводности в различных областях.
Одной из целей данной работы является получение функции Грина первой краевой задачи в ограниченной области, граница которой движется по закону $\beta \sqrt t $. Нахождение этой функции в свою очередь позволяет выписать точное аналитическое решение в указанной области, которое также получено в текущей статье. Еще одной целью является показать согласованность результатов в ограниченной области $0 \leqslant x \leqslant \beta \sqrt t $, работы полученных методов функции Грина и методом рядов.
Для начала напомним метод функции Грина для ограниченной области с подвижной границей. Пусть ${{\bar {\Omega }}_{t}} = \left\{ {\left( {x,t} \right);0 \leqslant x \leqslant y\left( t \right),t \geqslant 0} \right\}$, где y(t) – непрерывно дифференцируемая функция. Тогда температурное поле T(x,t) может быть найдено в области Ωt как результат решения задачи
(1)
$\frac{{\partial T}}{{\partial t}} = a\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + f\left( {x,t} \right),~\,\,\,\,~0 < x < y\left( t \right),\,\,\,\,~t > 0,$(2)
$T{{\left. {\left( {x,t} \right)} \right|}_{{t = 0}}} = {{\varphi }_{0}}\left( x \right),\,\,\,\,~0 \leqslant x \leqslant y\left( 0 \right),\,\,\,\,~y\left( 0 \right) \geqslant 0,$(3)
$T{{\left. {\left( {x,t} \right)} \right|}_{{x = 0}}} = {{\varphi }_{1}}\left( t \right),~\,\,\,~t \geqslant 0,$(4)
$T{{\left. {\left( {x,t} \right)} \right|}_{{x = y\left( t \right)}}} = {{\varphi }_{2}}\left( t \right),~\,\,\,\,~t \geqslant 0.$Функция Грина $G\left( {x,t,x{\kern 1pt} ',\tau } \right)$ для задачи (1)–(4) является решением
(5)
$\frac{{\partial G}}{{\partial t}} = a_{{\overline {\partial {{t}^{2}}} }}^{{{{\partial }^{2}}G}},\,\,\,\,~0 < x < y\left( t \right),\,\,\,\,~t > \tau ,$(6)
$G\left( {x,t,x{\kern 1pt} ',{{{\left. {\tau )} \right|}}_{{t = \tau }}} = \delta (x - x{\kern 1pt} '} \right),~\,\,\,\,0 < x < y\left( \tau \right),$(7)
$G(x,t,x{\kern 1pt} ',{{\left. {\tau )} \right|}_{{x = 0}}} = {{\left. {G(x,t,x{\kern 1pt} ',\tau )} \right|}_{{t = y\left( x \right)}}} = 0,\,\,\,\,~~t > \tau .$Интегральное представление (1)–(4) будет иметь вид
(8)
$\begin{gathered} T\left( {x,t} \right) = \int\limits_0^{y\left( 0 \right)} {T\left( {x{\kern 1pt} ',\tau } \right)} G{{\left. {\left( {x,t,x{\kern 1pt} ',\tau } \right)} \right|}_{{\tau = 0}}}dx{\kern 1pt} '\,\, + a{{\int\limits_0^t {\left[ {T\left( {x{\kern 1pt} ',\tau } \right)\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right]} }_{{x{\kern 1pt} ' = 0}}}d\tau - \\ - \,\,a{{\int\limits_0^t {\left[ {T\left( {x{\kern 1pt} ',\tau } \right)\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right]} }_{{x{\kern 1pt} ' = y\left( \tau \right)}}}d\tau + \int\limits_0^t {\int\limits_0^{y\left( \tau \right)} {f\left( {x{\kern 1pt} ',\tau } \right)} } G\left( {x,t,x{\kern 1pt} ',\tau } \right)d\tau dx{\kern 1pt} '. \\ \end{gathered} $Первая краевая задача в области ${{\Omega }_{{\,t}}} = \left\{ {\left( {x,t} \right);0 \leqslant x \leqslant \beta \sqrt t ,t \geqslant 0} \right\}$
Температурное поле может быть найдено в результате решения задачи
(9)
$\frac{{\partial T}}{{\partial t}} = a\frac{{{{\partial }^{2}}T}}{{\partial {{x}^{2}}}} + f\left( {x,t} \right),~\,\,\,~0 < x < \beta \sqrt \tau ,~\,\,\,~t > 0,$(10)
$T{{\left. {\left( {x,t} \right)} \right|}_{{x = 0}}} = {{\varphi }_{1}}\left( t \right),~\,\,\,\,~t \geqslant 0,$(11)
$T{{\left. {\left( {x,t} \right)} \right|}_{{x = \beta \sqrt t }}} = {{\varphi }_{2}}\left( t \right),\,\,\,\,~~t \geqslant 0.$Начальное условие (2) в этом случае не задается, так как при t = 0 область вырождается в точку. Функция Грина $G\left( {x,t,x{\kern 1pt} ',\tau } \right)$ для задачи (9)–(11) будет являться решением задачи
(12)
$\frac{{\partial G}}{{\partial t}} = a_{{\overline {\partial {{t}^{2}}} }}^{{{{\partial }^{2}}G}},~\,\,\,\,~~0 < x < \beta \sqrt t ,~\,\,\,\,~t > \tau ,$(13)
$G\left( {x,t,x{\kern 1pt} ',{{{\left. {\tau {\kern 1pt} ')} \right|}}_{{t = \tau }}} = \delta (x - x{\kern 1pt} '} \right),\,\,\,\,~0 < x < \beta \sqrt \tau ,$(14)
$G{{\left. {\left( {x,t,x{\kern 1pt} ',\tau } \right)} \right|}_{{x = 0}}} = 0,\,\,\,\,~~t > \tau ,$(15)
$G{{\left. {\left( {x,t,x{\kern 1pt} ',\tau } \right)} \right|}_{{x = \beta \sqrt t }}} = 0,\,\,\,\,~~t > \tau .$Интегральное представление будет иметь вид
(16)
$T\left( {x,t} \right) = a\int\limits_0^t {\left[ {{{{\left( {T\left( {x{\kern 1pt} ',\tau } \right)\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right)}}_{{x{\kern 1pt} ' = 0}}} - {{{\left( {T\left( {x{\kern 1pt} ',\tau } \right)\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right)}}_{{x{\kern 1pt} ' = \beta \sqrt \tau }}}~~} \right]d\tau } + \int\limits_0^t {d\tau } \int\limits_0^{\beta \sqrt t } {f\left( {x{\kern 1pt} ',\tau } \right)} G\left( {x,t,x{\kern 1pt} ',\tau } \right)dx{\kern 1pt} '.$Функция Грина первой краевой задачи в области ${{\Omega }_{{\,t}}} = \left\{ {\left( {x,t} \right);0 \leqslant x \leqslant \beta \sqrt t ,t \geqslant 0} \right\}$
Найдем аналитический вид функции Грина $G\left( {x,t,x{\kern 1pt} ',\tau } \right)$ задачи (12)–(15). Эту задачу можно переписать в эквивалентной форме
(17)
$\frac{{\partial G}}{{\partial t}} = a_{{\overline {\partial {{t}^{2}}} }}^{{{{\partial }^{2}}G}} + \delta \left( {t - \tau } \right)\delta \left( {x - x{\kern 1pt} '} \right),~\,\,\,0 < x < \beta \sqrt t ,~\,\,\,\,t > \tau ,$(18)
$G{{\left. {\left( {x,t,x{\kern 1pt} ',\tau } \right)} \right|}_{{t = 0}}} = 0,~~x \geqslant 0,$(19)
$G{{\left. {\left( {x,t,x{\kern 1pt} ',\tau } \right)} \right|}_{{x = 0}}} = 0,\,\,\,\,~~t > \tau ,$(20)
$G{{\left. {\left( {x,t,x{\kern 1pt} ',\tau } \right)} \right|}_{{x = \beta \sqrt t }}} = 0,\,\,\,\,~~t > \tau .$Введем переменные
(21)
${{x}_{1}} = \frac{x}{{\sqrt {2at} }},\,\,\,\,\theta = \frac{1}{2}\ln t~\left( {t = {{e}^{{2\theta }}}} \right).$Тогда задача (12)–(15) примет вид
(22)
$\begin{gathered} \frac{{{{\partial }^{2}}G}}{{\partial x_{1}^{2}}} + {{x}_{1}}\frac{{\partial G}}{{\partial {{x}_{1}}}} = \frac{{\partial G}}{{\partial \theta }} - 2{{e}^{{2\theta }}}\delta \left( {\sqrt {2a} {{x}_{1}}{{e}^{\theta }} - x{\kern 1pt} '} \right)\delta \left( {{{e}^{{2\theta }}} - \tau } \right), \\ 0 < {{x}_{1}} < \frac{\beta }{{\sqrt {2a} }},\,\,\,\, - \infty < \theta < + \infty . \\ \end{gathered} $(23)
${{\left. G \right|}_{{{{x}_{1}}}}} = 0,~\,\,\,\,{{\left. G \right|}_{{{{x}_{1}} = 0}}} = 0,~\,\,\,\,\mathop {\lim G}\limits_{\theta \to - \infty } = 0.$Перейдем в пространство изображений Фурье
(24)
$\bar {G}\left( {{{x}_{1}},i\lambda ,x{\kern 1pt} ',\tau } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {G\left( {{{x}_{1}},\theta ,x{\kern 1pt} ',\tau } \right)} {{e}^{{ - i\lambda \theta }}}d\theta .$Предварительно вычислим интеграл
(25)
$I = 2\int\limits_{ - \infty }^{ + \infty } {{{e}^{{2\theta }}}\delta } \left( {\sqrt {2a} {{x}_{1}}{{e}^{\theta }} - x{\kern 1pt} '} \right)\delta \left( {{{e}^{\theta }} - \tau } \right){{e}^{{ - i\lambda \theta }}}d\theta .$Принимая ${{e}^{{2\theta }}} = z$, из (22) и учитывая, что $dz = 2{{e}^{{2\theta }}}d\theta $ и $d\theta = \frac{{dz}}{{2{{e}^{{2\theta }}}}} = \frac{1}{2}{{z}^{{ - 1}}}dz$, получим
(26)
$\begin{gathered} I = 2\int\limits_{ - \infty }^{ + \infty } {z\delta } \left( {{{x}_{1}}\sqrt {2az} - x{\kern 1pt} '} \right)\delta \left( {z - \tau } \right){{z}^{{ - \frac{{i\lambda }}{2}}}}\frac{1}{2}{{z}^{{ - 1}}}dz = \int\limits_0^{ + \infty } {\delta \left( {{{x}_{1}}\sqrt {2az} - x{\kern 1pt} '} \right)} \delta \left( {z - \tau } \right){{z}^{{ - \frac{{i\lambda }}{2}}}}dz = \\ = \delta \left( {{{x}_{1}}\sqrt {2a\tau } - x{\kern 1pt} '} \right){{\tau }^{{ - \frac{{i\lambda }}{2}}}}. \\ \end{gathered} $Применим теперь интегральное преобразование (24) к уравнению (22), считая $G \to 0$ при $~\theta \to \infty $ и вводя обозначения ${{\beta }_{0}} = \frac{\beta }{{\sqrt {2a} }}$, ${{\xi }_{0}} = \frac{{x{\kern 1pt} '}}{{\sqrt {2a\tau } }}$, получим
(27)
$\frac{{{{{\text{d}}}^{2}}\bar {G}}}{{{\text{d}}x_{1}^{2}}} + {{x}_{1}}\frac{{{\text{d}}\bar {G}}}{{{\text{d}}{{x}_{1}}}} - i\lambda \bar {G} = ~ - \frac{1}{{\sqrt {2\pi } }}\delta \left( {{{x}_{1}}\sqrt {2a\tau } - x{\kern 1pt} '} \right){{\tau }^{{ - \frac{{i\lambda }}{2}}}},$(28)
${{\left. {\bar {G}} \right|}_{{{{x}_{1}} = {{\beta }_{0}}}}} = 0,\,\,\,\,{{\left. {\bar {G}} \right|}_{{{{x}_{1}} = 0}}} = 0.~$Задача (27)–(28) эквивалентна следующей:
(32)
${{\left. {\bar {G}} \right|}_{{{{x}_{1}} = {{\xi }_{0}} - 0}}} = {{\left. {\bar {G}} \right|}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}},$(33)
${{\left. {\frac{{d\bar {G}}}{{d{{x}_{1}}}}} \right|}_{{{{x}_{1}} = {{\xi }_{0}} - 0}}} - {{\left. {\frac{{d\bar {G}}}{{d{{x}_{1}}}}} \right|}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}} = \frac{1}{{2\sqrt {a\pi } }}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}.$Вопрос эквивалентности задач (27)–(28) и (29)–(33) подробно рассмотрен в [3].
Уравнение (29) является уравнением Вебера, частными решениями которого являются функции
(34)
$\left\{ \begin{gathered} {{e}^{{\frac{{ - x_{1}^{2}}}{4}}}}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right),~\,\,\,\,~{{e}^{{\frac{{ - x_{1}^{2}}}{4}}}}{{D}_{{ - 1 - i\lambda }}}\left( { - {{x}_{1}}} \right), \hfill \\ {{e}^{{\frac{{ - x_{1}^{2}}}{4}}}}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right),\,\,\,\,~{{e}^{{\frac{{ - x_{1}^{2}}}{4}}}}{{D}_{{i\lambda }}}\left( { - i{{x}_{1}}} \right), \hfill \\ \end{gathered} \right.$(35)
$\bar {G} = {{e}^{{\frac{{ - x_{1}^{2}}}{4}}}}\left[ {{{c}_{1}}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + {{c}_{2}}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)} \right],\,\,\,\,~0 < {{x}_{1}} < {{\xi }_{0}},$(36)
$\bar {G} = {{e}^{{\frac{{ - x_{1}^{2}}}{4}}}}\left[ {{{c}_{3}}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + {{c}_{4}}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)} \right],\,\,\,\,~{{\xi }_{0}} < {{x}_{1}} < {{\beta }_{0}}.$Используя условия (32) и (33), получим систему
(37)
$\left\{ \begin{gathered} {{c}_{1}}{{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right) + {{c}_{2}}{{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right) = {{c}_{3}}{{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right) + {{c}_{4}}{{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right), \hfill \\ {{\left. {{{c}_{1}}\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + \frac{{d{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}_{{{{x}_{1}} = {{\xi }_{0}} - 0}}} + {{\left. {{{c}_{2}}\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right) + \frac{{d{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}_{{{{x}_{1}} = {{\xi }_{0}} - 0}}} = \hfill \\ {{\left. { = {{c}_{3}}\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + \frac{{d{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}} + {{\left. {{{c}_{4}}\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right) + \frac{{d{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}} + \hfill \\ + \,\,\frac{1}{{2\sqrt {a\pi } }}{{e}^{{\frac{{\xi _{0}^{2}}}{4}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}. \hfill \\ \end{gathered} \right.$Найдем выражения постоянных ${{c}_{1}},\,\,~{{c}_{2}}$ через $~{{c}_{3}},~\,\,{{c}_{4}}$. Для этого воспользуемся методом Крамера и выражением для вронскиана функции параболического цилиндра [9]
(38)
${{D}_{\nu }}\left( z \right)\frac{d}{{dz}}{{D}_{{ - \nu - 1}}}\left( {iz} \right) - {{D}_{{ - \nu - 1}}}\left( {iz} \right)\frac{d}{{dz}}{{D}_{\nu }}\left( z \right) = - i{{e}^{{\frac{{ - \nu \pi }}{2}}}}.$Получаем ${{с}_{1}} = \frac{{{{\Delta }_{1}}}}{\Delta }$, ${{с}_{2}} = \frac{{{{\Delta }_{2}}}}{\Delta }$, где
(39)
$\Delta = {{\left. {\left| {\begin{array}{*{20}{c}} {{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right)}&{{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)} \\ {\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + \frac{{d{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]}&{\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right) + \frac{{d{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \end{array}} \right|} \right|}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}} = {{e}^{{ - \frac{{\lambda \pi }}{2}}}},$(40)
${{\Delta }_{1}} = \left| {\begin{array}{*{20}{c}} {[{{c}_{3}}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + {{c}_{4}}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right){{{\left. ] \right|}}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}}}&{{{{\left. {{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)} \right|}}_{{{{x}_{1}} = {{\xi }_{0}} - 0}}}} \\ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{c}_{3}}{{{\left. {\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + \frac{{d{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}} + } \\ {{{{\left. { + \,\,{{c}_{4}}\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right) + \frac{{d{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}} + } \end{array}} \\ { + \,\,\frac{1}{{2\sqrt {a\pi } }}{{e}^{{\frac{{\xi _{0}^{2}}}{4}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}} \end{array}}&{{{{\left. {\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right) + \frac{{d{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}}_{{{{x}_{1}} = {{\xi }_{0}} - 0}}} + } \end{array}} \right|,$(41)
${{\Delta }_{2}} = \left| {\begin{array}{*{20}{c}} {{{{\left. {{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right)} \right|}}_{{{{x}_{1}} = {{\xi }_{0}} - 0}}}}&{{{{\left. {\left[ {{{c}_{3}}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + {{c}_{4}}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)} \right]} \right|}}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}}} \\ {{{{\left. {\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + \frac{{d{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}}_{{{{x}_{1}} = {{\xi }_{0}} - 0}}}}&\begin{gathered} {{\left. {{{c}_{3}}\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right) + \frac{{d{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}} + \\ + \,\,{{\left. {{{c}_{4}}\left[ { - \frac{{{{x}_{1}}}}{2}{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right) + \frac{{d{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right)}}{{d{{x}_{1}}}}} \right]} \right|}_{{{{x}_{1}} = {{\xi }_{0}} + 0}}} + \\ + \frac{1}{{2\sqrt {a\pi } }}{{e}^{{\frac{{\xi _{0}^{2}}}{4}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}} \\ \end{gathered} \end{array}} \right|.$Преобразовывая далее (40 и (41), находим
(42)
${{\Delta }_{1}} = {{e}^{{ - \frac{{\lambda \pi }}{2}}}}{{c}_{3}} - {{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right)\frac{{{{е}^{{\frac{{\xi _{0}^{2}}}{4}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }},$(43)
${{\Delta }_{2}} = {{e}^{{ - \frac{{\lambda \pi }}{2}}}}{{c}_{4}} + {{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right)\frac{{{{е}^{{\frac{{\xi _{0}^{2}}}{4}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}.$Откуда получаем
(44)
${{c}_{1}} = {{c}_{3}} - {{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right)\frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }},$(45)
${{c}_{2}} = {{c}_{4}} + {{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right)\frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}.$Используя условия (30) ${{\left. {\bar {G}} \right|}_{{{{x}_{1}} = {{\beta }_{0}}}}} = 0$ и (31) ${{\left. {\bar {G}} \right|}_{{{{x}_{1}} = 0}}} = 0$ получаем систему на с3 и с4:
(46)
$\left\{ {\begin{array}{*{20}{c}} {\left[ {{{c}_{3}} - {{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right)\frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}} \right]{{D}_{{ - 1 - i\lambda }}}\left( 0 \right) + \left[ {{{c}_{4}} + {{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right)\frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}} \right]~{{D}_{{i\lambda }}}\left( 0 \right) = 0,} \\ {{{c}_{3}}{{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right) + {{c}_{4}}{{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right) = 0.} \end{array}} \right.$Следовательно,
(47)
${{c}_{3}} = {{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right)\frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}\frac{{{{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)}}{{{{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)}}$(48)
${{c}_{3}} = \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}{{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right)}}{{2\sqrt {a\pi } \left[ {{{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)} \right]}}\left[ {{{D}_{{ - 1 - i\lambda }}}\left( 0 \right){{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right) - {{D}_{{i\lambda }}}\left( 0 \right){{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right)} \right].$Так как ${{c}_{4}} = - {{c}_{3}}\frac{{{{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right)}}{{{{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right)}}$, то
(49)
${{c}_{4}} = - \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}{{D}_{{ - 1 - i\lambda }}}\left( {i{{\beta }_{0}}} \right)}}{{2\sqrt {a\pi } {{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)}}\left[ {{{D}_{{ - 1 - i\lambda }}}\left( 0 \right){{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)} \right].$Подставляя (48) и (49) в (44) и (45) находим ${{c}_{1}},~{{c}_{2}}$:
(50)
${{c}_{1}} = \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}\frac{{{{D}_{{i\lambda }}}\left( 0 \right)\left[ {{{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right) - {{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right)} \right]}}{{{{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)}},$(51)
${{c}_{2}} = \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}\frac{{{{D}_{{ - 1 - i\lambda }}}\left( 0 \right)\left[ { - {{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right) + {{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right)} \right]}}{{{{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)}}.$Тогда решение задачи (29)–(33) примет вид
(52)
$\bar {G} = \left\{ \begin{gathered} \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2} - \frac{{x_{1}^{2}}}{4}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}\frac{{{{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right) - {{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right)}}{{{{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)}}[{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right){{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right) - \hfill \\ - \,\,{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right)],\,\,\,\,0 < {{x}_{1}} < {{\xi }_{0}}, \hfill \\ \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} + \frac{{\lambda \pi }}{2} - \frac{{x_{1}^{2}}}{4}}}}{{\tau }^{{ - \frac{1}{2}\left( {i\lambda + 1} \right)}}}}}{{2\sqrt {a\pi } }}\frac{{{{D}_{{ - 1 - i\lambda }}}\left( 0 \right){{D}_{{i\lambda }}}\left( {i{{\xi }_{0}}} \right) - {{D}_{{i\lambda }}}\left( 0 \right){{D}_{{ - 1 - i\lambda }}}\left( {{{\xi }_{0}}} \right)}}{{{{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - 1 - i\lambda }}}\left( 0 \right) - {{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right){{D}_{{i\lambda }}}\left( 0 \right)}}[{{D}_{{ - 1 - i\lambda }}}\left( {{{x}_{1}}} \right){{D}_{{i\lambda }}}\left( {i{{\beta }_{0}}} \right) - \hfill \\ - \,\,{{D}_{{i\lambda }}}\left( {i{{x}_{1}}} \right){{D}_{{ - 1 - i\lambda }}}\left( {{{\beta }_{0}}} \right)],\,\,\,{{\xi }_{0}} < {{x}_{1}} < {{\beta }_{0}}. \hfill \\ \end{gathered} \right.$Используя замену (21) и применяя обратное преобразование Фурье
$\begin{gathered} G\left( {{{x}_{1}},t,x{\kern 1pt} ',\tau } \right) = G\left( {{{x}_{1}},\theta ,x{\kern 1pt} ',\tau } \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_{ - \infty }^{ + \infty } {\bar {G}\left( {{{x}_{1}},i\lambda ,x{\kern 1pt} ',\tau } \right){{e}^{{i\lambda \theta }}}d\lambda } = \\ = - \frac{i}{{\sqrt {2\pi } }}\int\limits_{ - i\infty }^{ + i\infty } {\bar {G}\left( {{{x}_{1}},i\lambda ,x{\kern 1pt} ',\tau } \right)} {{e}^{{i\lambda \theta }}}d\left( {i\lambda } \right) = - \frac{i}{{\sqrt {2\pi } }}\int\limits_{ - i\infty }^{ + i\infty } {} \mathop \smallint \limits_{}^{} \bar {G}\left( {{{x}_{1}},p,x{\kern 1pt} ',\tau } \right){{e}^{{p\theta }}}dp = \\ = - \frac{i}{{\sqrt {2\pi } }}\int\limits_{ - i\infty }^{ + i\infty } {\bar {G}\left( {{{x}_{1}},p,x{\kern 1pt} ',\tau } \right){{e}^{{\frac{p}{2}\ln t}}}dp} = - \frac{i}{{\sqrt {2\pi } }}\int\limits_{ - i\infty }^{ + i\infty } {\bar {G}\left( {{{x}_{1}},p,x{\kern 1pt} ',\tau } \right)} {{e}^{{{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}}}}dp \\ \end{gathered} $
к решению (52), получаем
(53)
$\begin{gathered} G\left( {{{x}_{1}},t,{{\xi }_{0}},\tau } \right) = \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} - \frac{{x_{1}^{2}}}{4}}}}}}{{2\pi i\sqrt {2a\tau } }}\,\int\limits_{ - i\infty }^{ + i\infty } {\frac{{{{D}_{p}}\left( {i{{\xi }_{0}}} \right){{D}_{{ - p - 1}}}\left( {{{\beta }_{0}}} \right) - {{D}_{p}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - p - 1}}}\left( {{{\xi }_{0}}} \right)}}{{{{D}_{p}}\left( {i{{\beta }_{0}}} \right){{D}_{{ - p - 1}}}\left( 0 \right) - {{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {{{\beta }_{0}}} \right)}}} \times \\ \times \,\,\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {{{x}_{1}}} \right) - {{D}_{{ - p - 1}}}\left( 0 \right){{D}_{p}}\left( {i{{x}_{1}}} \right)} \right]{{e}^{{ - \frac{\pi }{2}pi}}}{{\left( {\frac{t}{\tau }} \right)}^{{\frac{p}{2}}}}dp. \\ \end{gathered} $В переменных x, x', t, τ функция Грина (53) будет записана в виде
(54)
$\begin{gathered} G\left( {x,t,x',\tau } \right) = \frac{{{{e}^{{\frac{1}{{8a}}\left[ {\frac{{x{{'}^{2}}}}{\tau } - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{{2\pi i\sqrt {2a\pi \tau } }}\mathop \smallint \limits_{ - i\infty }^{ + i\infty } \frac{{{{D}_{p}}\left( {\frac{{ix{\kern 1pt} '}}{{\sqrt {2a\tau } }}} \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{{ - p - 1}}}\left( {\frac{{x{\kern 1pt} '}}{{\sqrt {2a\tau } }}} \right){{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right)}}{{{{D}_{{ - p - 1}}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right) - {{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)}} \times \\ \times \,\,\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{ - p - 1}}}\left( 0 \right){{D}_{p}}\left( {i\frac{x}{{\sqrt {2at} }}} \right)} \right]{{e}^{{ - \frac{\pi }{2}pi}}}{{\left( {\frac{t}{\tau }} \right)}^{{\frac{p}{2}}}}dp. \\ \end{gathered} $Целью дальнейших преобразований будет получение аналитического вида функции Грина задачи (29)–(33) в виде ряда. Для этого, используя согласно [8]
(55)
${{D}_{p}}(z) = \frac{{\Gamma \left( {p + 1} \right)}}{{\sqrt {2\pi } }}\left[ {{{e}^{{\frac{\pi }{2}pi}}}{{D}_{{ - p - 1}}}\left( {iz} \right) - {{e}^{{ - \frac{\pi }{2}pi}}}{{D}_{{ - p - 1}}}\left( { - iz} \right)} \right],$(56)
$\begin{gathered} G\left( {{{x}_{1}},t,{{\xi }_{0}},\tau } \right) = \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} - \frac{{x_{1}^{2}}}{4}}}}}}{{4\pi i\sqrt {a\pi \tau } }}\int\limits_{ - i\infty }^{ + i\infty } {\Gamma \left( {p + 1} \right)} \frac{{{{D}_{{ - p - 1}}}\left( { - {{\xi }_{0}}} \right){{D}_{{ - p - 1}}}\left( {{{\beta }_{0}}} \right) - {{D}_{{ - p - 1}}}\left( {{{\xi }_{0}}} \right){{D}_{{ - p - 1}}}\left( { - {{\beta }_{0}}} \right)}}{{{{D}_{{ - p - 1}}}\left( { - {{\beta }_{0}}} \right) - {{D}_{{ - p - 1}}}\left( {{{\beta }_{0}}} \right)}} \times \\ \times \,\,\left[ {{{D}_{{ - p - 1}}}\left( {{{x}_{1}}} \right) - {{D}_{{ - p - 1}}}\left( { - {{x}_{1}}} \right)} \right]{{\left( {\frac{t}{\tau }} \right)}^{{\frac{p}{2}}}}dp. \\ \end{gathered} $В переменных x, x', t, $\tau $ (56) примет вид
(57)
$\begin{gathered} G\left( {x,t,x{\kern 1pt} ',\tau } \right) = \frac{{{{e}^{{\frac{1}{{8a}}\left[ {\frac{{x{\kern 1pt} {{'}^{2}}}}{\tau } - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{{4\pi i\sqrt {a\pi \tau } }}\int\limits_{ - i\infty }^{ + i\infty } {\Gamma \left( {p + 1} \right)} \times \\ \times \,\,\frac{{{{D}_{{ - p - 1}}}\left( { - \frac{{x{\kern 1pt} '}}{{\sqrt {2a\tau } }}} \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{{ - p - 1}}}\left( {\frac{{x{\kern 1pt} '}}{{\sqrt {2a\tau } }}} \right){{D}_{{ - p - 1}}}\left( { - \frac{\beta }{{\sqrt {2a} }}} \right)}}{{{{D}_{{ - p - 1}}}\left( { - \frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)}} \times \\ \times \,\,\left[ {{{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{ - p - 1}}}\left( { - \frac{x}{{\sqrt {2at} }}} \right)} \right]{{\left( {\frac{t}{\tau }} \right)}^{{\frac{p}{2}}}}dp. \\ \end{gathered} $Пусть
$\begin{gathered} F\left( p \right) = \Gamma \left( {p + 1} \right)\frac{{{{D}_{{ - p - 1}}}\left( { - {{\xi }_{0}}} \right){{D}_{{ - p - 1}}}\left( {{{\beta }_{0}}} \right) - {{D}_{{ - p - 1}}}\left( {{{\xi }_{0}}} \right){{D}_{{ - p - 1}}}\left( { - {{\beta }_{0}}} \right)}}{{{{D}_{{ - p - 1}}}\left( { - {{\beta }_{0}}} \right) - {{D}_{{ - p - 1}}}\left( {{{\beta }_{0}}} \right)}} \times \\ \times \,\,\left[ {{{D}_{{ - p - 1}}}\left( {{{x}_{1}}} \right) - {{D}_{{ - p - 1}}}\left( { - {{x}_{1}}} \right)} \right]{{\left( {\frac{t}{\tau }} \right)}^{{\frac{p}{2}}}}. \\ \end{gathered} $
Так как функция ${{D}_{p}}\left( z \right)$ является целой функцией переменного z и параметра p, то подынтегральная функция $F\left( p \right)$ является аналитической во всей комплексной плоскости p, за исключением простых полюсов в точках $p = - n~\left( {n = 1,2,3, \ldots } \right)$ и в точках $p = {{p}_{n}}$, где ${{p}_{n}}$ – нецелые корни уравнения
(58)
${{D}_{{ - p - 1}}}\left( { - {{\beta }_{0}}} \right) - {{D}_{{ - p - 1}}}\left( {{{\beta }_{0}}} \right) = 0.$Решение уравнений типа (58) представляет собой самостоятельную задачу. Насколько известно автору работы [5] и [6] являются первыми, рассматривающими этот вопрос. Далее по теореме о вычетах
(59)
$G\left( {{{x}_{1}},t,{{\xi }_{0}},\tau } \right) = \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} - \frac{{x_{1}^{2}}}{4}}}}}}{{4\pi i\sqrt {a\pi \tau } }}~\left( {2\pi i\left[ {\mathop \sum \limits_{n = 1}^\infty \mathop {res}\limits_{p = - n} F\left( p \right) + \mathop \sum \limits_{n = 1}^\infty \mathop {res}\limits_{p = {{p}_{n}}} F\left( p \right)} \right]} \right).$Используя свойства функции параболического цилиндра при целых p, а также пользуясь соотношениями для функции Эрмита [8]
$\begin{gathered} {{D}_{n}}\left( z \right) = {{e}^{{ - \frac{{{{z}^{2}}}}{4}}}}{{2}^{{ - \frac{n}{2}}}}{{H}_{n}}\left( {\frac{z}{{\sqrt 2 }}} \right), \\ \sum\limits_{n = 0}^\infty {\frac{{{{H}_{n}}\left( x \right){{H}_{n}}\left( y \right)}}{{{{2}^{n}}n!}}{{t}^{n}}} ~ = {{\left( {1 - {{t}^{2}}} \right)}^{{ - \frac{1}{2}}}}\exp \left( {\frac{{2xyt - \left( {{{x}^{2}} + {{y}^{2}}} \right){{t}^{2}}}}{{1 - {{t}^{2}}}}} \right),\,\,\,\,\left| t \right| < 1, \\ \end{gathered} $
$\begin{gathered} {{H}_{n}}\left( { - z} \right) = {{\left( { - 1} \right)}^{n}}{{H}_{n}}\left( z \right);\,\,\,~{{D}_{n}}\left( { - z} \right) = {{\left( { - 1} \right)}^{n}}{{D}_{n}}\left( z \right); \\ \mathop {\lim }\limits_{p \to - n} \left( {p + n} \right)\Gamma \left( {p + 1} \right) = \frac{{{{{\left( { - 1} \right)}}^{{n - 1}}}}}{{\left( {n - 1} \right)!}},\,\,\,\,n = 1,2 \ldots , \\ \end{gathered} $
получаем, что первая сумма в (59) равна нулю. Это означает, что функция Грина имеет
следующий вид
(60)
$\begin{gathered} G\left( {{{x}_{1}},t,x{\kern 1pt} ',\tau } \right) = \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} - \frac{{x_{1}^{2}}}{4}}}}}}{{2\sqrt {a\pi \tau } }}\mathop \sum \limits_{n = 1}^\infty \mathop {res}\limits_{p = {{p}_{n}}} F\left( p \right) = \frac{{{{e}^{{\frac{{\xi _{0}^{2}}}{4} - \frac{{x_{1}^{2}}}{4}}}}}}{{2\sqrt {a\pi \tau } }}\mathop \sum \limits_{n = 1}^\infty \Gamma \left( {{{p}_{n}} + 1} \right) \times \\ \times \frac{{{{D}_{{ - {{p}_{n}} - 1}}}\left( { - {{\xi }_{0}}} \right){{D}_{{ - {{p}_{n}} - 1}}}\left( {{{\beta }_{0}}} \right) - {{D}_{{ - {{p}_{n}} - 1}}}\left( {{{\xi }_{0}}} \right){{D}_{{ - {{p}_{n}} - 1}}}\left( { - {{\beta }_{0}}} \right)}}{{\frac{\partial }{{\partial p}}{{{\left. {\left[ {{{D}_{{ - p - 1}}}\left( { - {{\beta }_{0}}} \right) - {{D}_{{ - p - 1}}}\left( {{{\beta }_{0}}} \right)} \right]} \right|}}_{{p = {{p}_{n}}}}}}}\left[ {{{D}_{{ - {{p}_{n}} - 1}}}\left( {{{x}_{1}}} \right) - {{D}_{{ - {{p}_{n}} - 1}}}\left( { - {{x}_{1}}} \right)} \right]{{\left( {\frac{t}{\tau }} \right)}^{{\frac{{{{p}_{n}}}}{2}}}}, \\ \end{gathered} $Переходя к переменным x, x', t, τ в (60), получаем функцию Грина в виде ряда
(61)
$\begin{gathered} G\left( {x,t,x{\kern 1pt} ',\tau } \right) = \frac{{{{e}^{{\frac{1}{{8a}}\left( {\frac{{x{\kern 1pt} {{'}^{2}}}}{\tau } - \frac{{{{x}^{2}}}}{t}} \right)}}}}}{{2\sqrt {a\pi \tau } }}\sum\limits_{n = 1}^\infty {\Gamma \left( {{{p}_{n}} + 1} \right)} \times \\ \times \,\,\frac{{{{D}_{{ - {{p}_{n}} - 1}}}\left( { - \frac{{x{\kern 1pt} '}}{{\sqrt {2a\tau } }}} \right){{D}_{{ - {{p}_{n}} - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{{ - {{p}_{n}} - 1}}}\left( { - \frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - {{p}_{n}} - 1}}}\left( {\frac{{x{\kern 1pt} '}}{{\sqrt {2a\tau } }}} \right)}}{{\frac{\partial }{{\partial p}}{{{\left. {\left[ {{{D}_{{ - p - 1}}}\left( { - \frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)} \right]} \right|}}_{{p = {{p}_{n}}}}}}} \times \\ \times \,\,\left[ {{{D}_{{ - {{p}_{n}} - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{ - {{p}_{n}} - 1}}}\left( { - \frac{x}{{\sqrt {2at} }}} \right)} \right]{{\left( {\frac{t}{\tau }} \right)}^{{\frac{{{{p}_{n}}}}{2}}}}, \\ \end{gathered} $Подведем итог этой части работы. Формулы (54) и (57) – явный вид функции Грина первой краевой задачи в области ${{\Omega }_{t}} = \left\{ {\left( {x,t} \right);0 \leqslant x \leqslant \beta \sqrt t ,t \geqslant 0} \right\}$ в интегральной форме, а формула (61) – в виде ряда.
Приложение. Согласованность результатов. Вопрос согласованности результатов, полученных разными методами, играет очень важную роль. В связи с этим в качестве приложения результатов этой работы найдем с помощью описанного выше метода температурную функцию, полученную в известной работе Э.М. Карташова и Б.Я. Любова [7] с помощью метода рядов. Метод рядов является очень мощным инструментом и среди прочего позволяет решить краевую задачу (1)–(4) при условии, что функции ${{\varphi }_{1}}\left( t \right)$ и ${{\varphi }_{2}}\left( t \right)$ допускают разложение в виде рядов
(62)
${{\varphi }_{1}}\left( t \right) = \sum\limits_{k = - \infty }^{k = + \infty } {{{b}_{{\frac{k}{n}}}}{{t}^{{\frac{k}{n}}}}} ,~\,\,\,\,~t > 0,$(63)
${{\varphi }_{2}}\left( t \right) = \sum\limits_{k = - \infty }^{k = + \infty } {{{c}_{{\frac{k}{m}}}}{{t}^{{\frac{k}{m}}}}} ,\,\,\,\,~~t > 0.$В этом случае, согласно [7], решение в области
(64)
${{\Omega }_{t}} = \left\{ {\left( {x,t} \right);0 \leqslant x \leqslant \gamma \sqrt {2at} ,t \geqslant 0} \right\}$(65)
$\begin{gathered} T\left( {x,t} \right) = {{e}^{{ - \frac{{{{x}^{2}}}}{{8at}}}}}\left[ {\mathop \sum \limits_{k = - \infty }^{k = + \infty } {{b}_{{\frac{k}{n}}}}\frac{{{{D}_{{ - 2\frac{k}{n} - 1}}}\left( \gamma \right){{D}_{{2\frac{k}{n}}}}\left( {i\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{2\frac{k}{n}}}}\left( {i\gamma } \right){{D}_{{ - 2\frac{k}{n} - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right)}}{{{{D}_{{ - 2\frac{k}{n} - 1}}}\left( \gamma \right){{D}_{{2\frac{k}{n}}}}\left( 0 \right) - {{D}_{{2\frac{k}{n}}}}\left( {i\gamma } \right){{D}_{{ - 2\frac{k}{n} - 1}}}\left( 0 \right)}}{{t}^{{\frac{k}{n}}}} + } \right. \\ \left. { + \,\,{{e}^{{\frac{{{{\gamma }^{2}}}}{4}}}}\mathop \sum \limits_{k = - \infty }^{k = + \infty } {{c}_{{\frac{k}{m}}}}\frac{{{{D}_{{2\frac{k}{m}}}}\left( 0 \right){{D}_{{ - 2\frac{k}{m} - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{ - 2\frac{k}{m} - 1}}}\left( 0 \right){{D}_{{2\frac{k}{m}}}}\left( {i\frac{x}{{\sqrt {2at} }}} \right)}}{{{{D}_{{ - 2\frac{k}{m} - 1}}}\left( \gamma \right){{D}_{{2\frac{k}{m}}}}\left( 0 \right) - {{D}_{{2\frac{k}{m}}}}\left( {i\gamma } \right){{D}_{{ - 2\frac{k}{m} - 1}}}\left( 0 \right)}}{{t}^{{\frac{k}{m}}}}} \right]. \\ \end{gathered} $Используя интегральное представление температурного поля (16), а также явный вид полученной функции Грина (54) покажем, что решение (65) может быть получено и с помощью приведенного выше подхода. Согласно ему температурная функция при граничных условиях (62) и (63) будет представлена в виде
(66)
$T\left( {x,t} \right) = a\int\limits_0^t {\sum\limits_{k = - \infty }^{k = + \infty } {\left[ {{{b}_{{\frac{k}{n}}}}{{\tau }^{{\frac{k}{n}}}}{{{\left. {\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right|}}_{{x{\kern 1pt} ' = 0}}} - {{c}_{{\frac{k}{m}}}}{{\tau }^{{\frac{k}{m}}}}{{{\left. {\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right|}}_{{x{\kern 1pt} ' = \beta \sqrt \tau }}}} \right]d\tau } } .$Очевидно, что для ее получения потребуется найти частные производные $\frac{{\partial G}}{{\partial x{\kern 1pt} '}}$ на границах области. Для удобства найдем эти частные производные в области ${{\Omega }_{t}} = \left\{ {\left( {x,t} \right);0 \leqslant x \leqslant \beta \sqrt t ,t \geqslant 0} \right\}$, а затем запишем полученный результат в области (65). Продифференцировав частным образом (54) и воспользовавшись (55), получаем
(67)
${{\left. {\frac{{\partial G\left( {x,t,x{\kern 1pt} ',\tau } \right)}}{{\partial x'}}} \right|}_{{x' = 0}}} = \frac{{{{e}^{{ - \frac{{{{x}^{2}}}}{{8at}}}}}}}{{2\pi {\text{i}}\sqrt {2a\tau } }}\int\limits_{ - i\infty }^{ + i\infty } {\frac{{\left[ {{{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{p}}\left( {i\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{p}}\left( {\frac{{i\beta }}{{\sqrt {2a} }}} \right){{D}_{p}}\left( {\frac{{ix}}{{\sqrt {2at} }}} \right)} \right]}}{{{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{p}}\left( {\frac{{i\beta }}{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right)}}} {{\left( {\frac{t}{\tau }} \right)}^{{\frac{p}{2}}}}dp.$
${{\left. {\frac{{\partial G\left( {x,t,x{\kern 1pt} ',\tau } \right)}}{{\partial x{\kern 1pt} '}}} \right|}_{{x{\kern 1pt} ' = \beta \sqrt \tau }}} = \frac{{{{e}^{{\frac{1}{{8a}}\left[ {{{{\beta }}^{2}} - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{{2\pi {\text{i}}\sqrt {2a\tau } }}\int\limits_{ - i\infty }^{ + i\infty } {\frac{{\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{ - p - 1}}}\left( 0 \right){{D}_{p}}\left( {\frac{{ix}}{{\sqrt {2at} }}} \right)} \right]}}{{{{D}_{p}}\left( {\frac{{i\beta }}{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right) - {{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)}}} {{\left( {\frac{t}{\tau }} \right)}^{{\frac{p}{2}}}}dp.$
Далее, применяя теорему о вычетах, найдем интеграл
$\begin{gathered} \mathop \smallint \limits_0^t {{b}_{{\frac{k}{n}}}}{{\tau }^{{\frac{k}{n}}}}{{\left. {\frac{{\partial G}}{{\partial x'}}} \right|}_{{x' = 0}}}d\tau \, = \,\mathop \smallint \limits_0^t \frac{{{{e}^{{ - \frac{{{{x}^{2}}}}{{8at}}}}}}}{{4\pi ia\tau }}{{b}_{{\frac{k}{n}}}}{{\tau }^{{\frac{k}{n}}}}\left[ {\mathop \smallint \limits_{ - i\infty }^{i\infty } \frac{{{{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{p}}\left( {i\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right)}}{{{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right)}}\frac{{{{t}^{{p/2}}}}}{{{{\tau }^{{p/2}}}}}dp} \right]d\tau = \\ = \mathop \smallint \limits_{c - i\infty }^{c + i\infty } \left[ {\frac{{{{e}^{{ - \frac{{{{x}^{2}}}}{{8at}}}}}}}{{4\pi ia}}\frac{{{{b}_{{\frac{k}{n}}}}\left[ {{{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{p}}\left( {i\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right)} \right]{{t}^{{p/2}}}}}{{{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right)}}\mathop \smallint \limits_0^t {{\tau }^{{\frac{k}{n} - \frac{p}{2} - 1}}}d\tau } \right]dp = \\ = \frac{{{{e}^{{ - \frac{{{{x}^{2}}}}{{8at}}}}}}}{{4\pi ia}}{{b}_{{\frac{k}{n}}}}\mathop \smallint \limits_{c - i\infty }^{c + i\infty } \frac{{\left[ {{{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{p}}\left( {i\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right)} \right]{{t}^{{\frac{p}{2} + \frac{k}{n} - \frac{p}{2}}}}}}{{\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right)} \right]\left( {\frac{k}{n} - \frac{p}{2}} \right)}}dp = \\ = \frac{{{{e}^{{ - \frac{{{{x}^{2}}}}{{8at}}}}}}}{{2\pi ia}}{{b}_{{\frac{k}{n}}}}\mathop \smallint \limits_{c - i\infty }^{c + i\infty } \frac{{\left[ {{{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{p}}\left( {i\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right)} \right]{{t}^{{\frac{k}{n}}}}}}{{\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right)} \right]\left( {2\frac{k}{n} - p} \right)}}dp = \\ = {{b}_{{\frac{k}{n}}}}\frac{{{{e}^{{ - \frac{{{{x}^{2}}}}{{8at}}}}}}}{a}\frac{{{{D}_{{ - 2\frac{k}{n} - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{2\frac{k}{n}}}}\left( {i\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{2\frac{k}{n}}}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - 2\frac{k}{n} - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right)}}{{{{D}_{{2\frac{k}{n}}}}\left( 0 \right){{D}_{{ - 2\frac{k}{n} - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{{2\frac{k}{n}}}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - 2\frac{k}{n} - 1}}}\left( 0 \right)}}{{t}^{{\frac{k}{n}}}}. \\ \end{gathered} $
Т.е.
(69)
$\int\limits_0^t {{{b}_{{\frac{k}{n}}}}{{\tau }^{{\frac{k}{n}}}}} {{\left. {\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right|}_{{x{\kern 1pt} ' = 0}}}d\tau = {{b}_{{\frac{k}{n}}}}\frac{{{{e}^{{ - \frac{{{{x}^{2}}}}{{8at}}}}}}}{a}\frac{{{{D}_{{ - 2\frac{k}{n} - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{2\frac{k}{n}}}}\left( {i\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{2\frac{k}{n}}}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - 2\frac{k}{n} - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right)}}{{{{D}_{{2\frac{k}{n}}}}\left( 0 \right){{D}_{{ - 2\frac{k}{n} - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right) - {{D}_{{2\frac{k}{n}}}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - 2\frac{k}{n} - 1}}}\left( 0 \right)}}{{t}^{{\frac{k}{n}}}}.$Используя аналогичные преобразования, найдем интеграл
$\begin{gathered} \mathop \smallint \limits_0^t {{c}_{{\frac{k}{m}}}}{{\tau }^{{\frac{k}{m}}}}{{\left. {\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right|}_{{x{\kern 1pt} ' = \beta \sqrt \tau }}}d\tau = \mathop \smallint \limits_0^t \frac{{{{e}^{{\frac{1}{{8a}}\left[ {{{\beta }^{2}} - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{{4\pi ia\tau }}{{c}_{{\frac{k}{m}}}}{{\tau }^{{\frac{k}{m}}}}\left[ {\mathop \smallint \limits_{ - i\infty }^{i\infty } \frac{{{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{p - 1}}}\left( 0 \right){{D}_{p}}\left( {\frac{{ix}}{{\sqrt {2at} }}} \right)}}{{{{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right) - {{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)}}\frac{{{{t}^{{p/2}}}}}{{{{\tau }^{{p/2}}}}}dp} \right]d\tau = \\ = \mathop \smallint \limits_{c - i\infty }^{c + i\infty } \left[ {\frac{{{{e}^{{\frac{1}{{8a}}\left[ {{{\beta }^{2}} - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{{4\pi ia}}\frac{{{{c}_{{\frac{k}{m}}}}\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{p - 1}}}\left( 0 \right){{D}_{p}}\left( {\frac{{ix}}{{\sqrt {2at} }}} \right)} \right]{{t}^{{p/2}}}}}{{{{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right) - {{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)}}\mathop \smallint \limits_0^t {{\tau }^{{\frac{k}{m} - \frac{p}{2} - 1}}}d\tau } \right]dp = \\ = \,\,\,\frac{{{{e}^{{\frac{1}{{8a}}\left[ {{{\beta }^{2}} - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{{4\pi ia}}2{{c}_{{\frac{k}{m}}}}\mathop \smallint \limits_{c - i\infty }^{c + i\infty } \frac{{\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{p - 1}}}\left( 0 \right){{D}_{p}}\left( {\frac{{ix}}{{\sqrt {2at} }}} \right)} \right]{{t}^{{p/2}}}{{t}^{{\frac{k}{m} - \frac{p}{2}}}}}}{{\left[ {{{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right) - {{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)} \right]\left( {\frac{k}{m} - \frac{p}{2}} \right)}}d\frac{p}{2} = \\ \end{gathered} $
$\begin{gathered} = \frac{{{{e}^{{\frac{1}{{8a}}\left[ {{{\beta }^{2}} - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{{4\pi ia}}2{{c}_{{\frac{k}{m}}}}\mathop \smallint \limits_{c - i\infty }^{c + i\infty } \frac{{\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{p - 1}}}\left( 0 \right){{D}_{p}}\left( {\frac{{ix}}{{\sqrt {2at} }}} \right)} \right]{{t}^{{\frac{k}{m}}}}}}{{\left[ {{{D}_{p}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - p - 1}}}\left( 0 \right) - {{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)} \right]\left( {2\frac{k}{m} - p} \right)}}dp = \\ = {{c}_{{\frac{k}{m}}}}\frac{{{{e}^{{\frac{1}{{8a}}\left[ {{{\beta }^{2}} - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{a}\frac{{\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{p - 1}}}\left( 0 \right){{D}_{p}}\left( {\frac{{ix}}{{\sqrt {2at} }}} \right)} \right]}}{{{{D}_{{2\frac{k}{m}}}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - 2\frac{k}{m} - 1}}}\left( 0 \right) - {{D}_{{2\frac{k}{m}}}}\left( 0 \right){{D}_{{ - 2\frac{k}{m} - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)}}{{t}^{{\frac{k}{m}}}}. \\ \end{gathered} $
Т.е.
(70)
$\int\limits_0^t {{{c}_{{\frac{k}{m}}}}{{\tau }^{{\frac{k}{m}}}}} {{\left. {\frac{{\partial G}}{{\partial x{\kern 1pt} '}}} \right|}_{{x{\kern 1pt} ' = \beta \sqrt \tau }}}d\tau = {{c}_{{\frac{k}{m}}}}\frac{{{{e}^{{\frac{1}{{8a}}\left[ {{{\beta }^{2}} - \frac{{{{x}^{2}}}}{t}} \right]}}}}}{a}\frac{{\left[ {{{D}_{p}}\left( 0 \right){{D}_{{ - p - 1}}}\left( {\frac{x}{{\sqrt {2at} }}} \right) - {{D}_{{p - 1}}}\left( 0 \right){{D}_{p}}\left( {\frac{{ix}}{{\sqrt {2at} }}} \right)} \right]}}{{{{D}_{{2\frac{k}{m}}}}\left( {i\frac{\beta }{{\sqrt {2a} }}} \right){{D}_{{ - 2\frac{k}{m} - 1}}}\left( 0 \right) - {{D}_{{2\frac{k}{m}}}}\left( 0 \right){{D}_{{ - 2\frac{k}{m} - 1}}}\left( {\frac{\beta }{{\sqrt {2a} }}} \right)}}{{t}^{{\frac{k}{m}}}}.$Подставляя далее (69) и (70) в (66), а также учитывая, что
получаем (65).ВЫВОДЫ
Получен явный вид функции Грина в интегральной форме и в виде ряда первой краевой задачи нестационарной теплопроводности в ограниченной области, граница которой движется по закону $\beta \sqrt t $. Показана согласованность результатов, полученных с помощью метода функции Грина, и другими авторами с использованием других подходов.
Список литературы
Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М. Высш. школа. 2001. С. 540.
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М.: URSS. 2012. С. 655.
Карташов Э.М., Кротов Г.С. Функции Грина в задачах нестационарной теплопроводности в области с границей, движущейся по корневой зависимости / Известия РАН. Энергетика. 2006. № 4. С. 134–149.
Антимиров М.Я. Функция Грина одномерного уравнения параболического типа при движении границы по закону $\beta \sqrt t $ / Латвийский математический ежегодник. Рига. Зинатне. 1973. С. 70–97.
Кротов Г.С. Корни трансцендентного уравнения с функцией параболического цилиндра при фиксированном значении аргумента. Тепловые вопросы в технике. 2015. Т. 7. № 7. С. 318–324.
Кротов Г.С. Корни функции параболического цилиндра при фиксированном значении аргумента / Ученые Записки МИТХТ. Москва. 2005. Выпуск 14. С. 41–48.
Карташов Э.М., Любов Б.Я. Метод решения краевых задач теплопроводности для области с границей, движущейся по параболическому закону / Журн. технической физики. V XVI. 1971. № 1. С. 3–16.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз. 1962. 1100 с.
Бейтман Г., Эрдейи А. Высшие трансцендентные функции. М.: Наука. 1966. Т. II. 330 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика
Пн.-пт.: 10.00-19.00