Известия РАН. Энергетика, 2021, № 3, стр. 70-90
Теплообмен и оптимизация панельных холодильников-излучателей перспективных космических аппаратов мегаваттного уровня мощности
Д. Н. Ильмов 1, *, Н. И. Филатов 1, С. Г. Черкасов 1
1 ГНЦ ФГУП “Центр Келдыша”
Москва, Россия
* E-mail: ilmovdn@mail.ru
Поступила в редакцию 04.08.2020
После доработки 23.04.2021
Принята к публикации 26.04.2021
Аннотация
Представлена уточненная методика приблизительного аналитического расчета холодильника-излучателя. Она предполагает расчет теплового состояния элемента трубы и ребра с последующим сопряжением решений. На основе полученных аналитических выражений для тепловых потоков от холодильника-излучателя проведен поиск оптимальных по массе геометрических параметров ребра постоянной толщины для излучателей мегаваттного уровня мощности.
Разработка различных конструкций холодильников-излучателей (ХИ) и методов их расчета в Советском Союзе и США началась еще в 60-х годах прошлого века. Предыдущими поколениями инженеров и ученых ракетно-космической промышленности были заложены основы проектирования ХИ [1, 2] и успешно реализованы в рамках создания космических аппаратов (КА) различного назначения, включая долговременные орбитальные станции “Мир” и МКС.
Сейчас для жизнеобеспечения большинства современных спутников с относительно небольшим потреблением энергии и небольшой необходимостью ее сброса в космическое пространство, как правило, применяются излучатели на основе аммиачных тепловых труб, работающие при температурах около 300 К с эффективной излучающей поверхностью порядка десятка квадратных метров и менее. Для расчета большинства конструкций ХИ, работающих на данных уровнях температуры, успешно применяются методы линеаризации уравнения радиационного теплообмена [2]. Корректность этих методов в данном диапазоне температур была многократно подтверждена экспериментально, в частности, результатами летной эксплуатации большого количества КА.
Другим широко известным направлением являются проектные работы по созданию высокотемпературных излучателей, предназначенных для электроэмиссионных ядерных энергетических установок (ЯЭУ). В РКК “Энергия” для ЯЭУ проекта “Геркулес” [3] были разработаны уникальные тепловые трубы на основе ниобиевых сплавов с жидкометаллическими теплоносителями, работающие при температурах порядка 1000 К. Наибольших результатов в области отработки раскладных ХИ удалось достичь в ходе работ над термоэмиссионными космическими ЯЭУ в рамках проекта РП-50 [4, 5]. На форсированном режиме продолжительностью до 1 года ЯЭУ должна вырабатывать 105 кВт электрической энергии. Соответственно, при системном КПД ЯЭУ равном 9.5%, тепловая мощность, отводимая ХИ, составляет около 1 МВт. Благодаря высокой средней температуре излучающей поверхности ХИ (около 800 К), площадь его поверхности для РП-50 относительно не велика и составляет около 60 м2 [5].
В настоящее время является актуальным создание нового класса КА с ЯЭУ и газотурбинным преобразователем энергии, работающим по циклу Брайтона [6, 7]. Такая энергетическая установка обладает высоким КПД и способна вырабатывать сотни и тысячи киловатт электрической энергии, что обеспечит качественный прорыв в развитии космической деятельности. Излучатель такого перспективного КА должен работать в среднем диапазоне температур, примерно от 400 до 700 К, который является не типичным для ранее разработанных устройств сброса тепла. В данном диапазоне температур нет надежных данных по использованию тепловых труб, поэтому может быть целесообразно применение традиционного панельного холодильника-излучателя (ПХИ) с прокачкой теплоносителя. Еще одна особенность – потребность больших излучающих площадей. При средней температуре ХИ около 500 К требуется более 300 м2 для сброса 1 МВт тепла. Последнее обстоятельство накладывает исключительные требования к оптимизации конструкции излучателя и свидетельствует об актуальности рассматриваемой задачи.
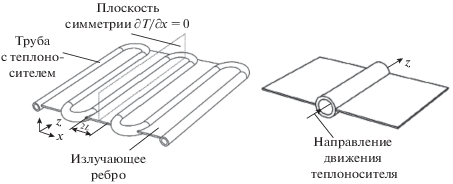
Объектом исследований в данной работе является наиболее простой “классический” холодильник-излучатель с ребрами постоянной толщины. Он представляет собой набор параллельных оребренных трубок (потоков), по которым циркулирует охлаждаемый теплоноситель (жидкий). Протяженность одного потока ХИ может быть велика, и тогда в действительности он может представлять собой изогнутую трубку (змеевик) с излучающими ребрами (рис. 1). Задача о точном расчете теплового состояния панели является частной и связана с доскональной проработкой конкретной конструкции. В более общем случае задачу целесообразно свести к двум одномерным: распространение тепла перпендикулярно потоку и остывание теплоносителя по мере его движения вдоль потока. Таким образом, типовой фрагмент “классического” холодильника-излучателя, для которого строится математическая модель, представляет собой прямолинейный круглый трубопровод и 2 ребра постоянной толщины, пристыкованные к трубе (рис. 1).
Будем считать, что ребра излучают с двух сторон. Полученные ниже результаты легко могут быть распространены на типовой элемент, например, с 4-мя или одним ребром, на случай, когда ребра излучают только с одной стороны.
Поскольку перспективные КА с мощной ЯЭУ разрабатываются в том числе для межпланетных полетов, будем считать, что удаленность КА от Земли более 250 км. Тогда влиянием атмосферы можно полностью пренебречь [1].
Пренебрежем также внешним потоком радиации от Солнца и Земли. Поток внешней радиации может быть минимизирован соответствующей ориентацией КА в пространстве, а также применением современных покрытий с высокой интегральной излучательной способностью $\varepsilon $ (более 0.9) и низкой поглощательной способностью (0.2 и менее) [8].
Расчеты элементов холодильника-излучателя в стационарном тепловом режиме на основе решения уравнения теплопроводной излучающей пластины представлены во многих работах. Как правило, применяются численные методы решения [1, 9–13]: вариационно-итерационный метод (VIM), метод разложения Адомиана (ADM), метод конечных элементов (FEM), гомотопический метод возмущений (HPM), метод конечных разностей. Отметим, что в работе [1] рассмотрены ребра с изменяющейся толщиной по ширине. В работах [14, 15] применяется аналитический метод расчета с решением в виде бесконечных рядов. Достаточно часто [2, 16–18], применяется линеаризация исходного уравнения, что позволяет получить приближенные аналитические решения задачи. Настоящая работа является развитием подхода [16–18], основанного на линеаризации.
Крайне упрощенно (предполагая, что теплопроводность материала ХИ достаточно велика) для сбрасываемой теплоты можно записать соотношения:
(1)
$Q = \frac{{{{{\tilde {T}}}_{L}} - {{{\tilde {T}}}_{W}}}}{{{{R}_{{CON}}}}},\,\,\,\,Q \approx \frac{{{{{\tilde {T}}}_{W}} - 0}}{{{{R}_{{RAD}}}}},$Из (2) следует, что для достижения наибольшего сбрасываемого тепла $Q$ следует стремиться к уменьшению термических сопротивлений как ${{R}_{{RAD}}},$ так и ${{R}_{{CON}}}.$ Путем выбора высокотеплопроводящих теплоносителей (жидкометаллических) либо организацией течения теплоносителя в развитом турбулентном режиме удается обеспечить высокие значения коэффициента конвективной теплоотдачи [12], причем оказывается ${{R}_{{RAD}}} \gg {{R}_{{CON}}},$ в результате чего ${{\tilde {T}}_{W}} = {{\tilde {T}}_{L}}\frac{{{{R}_{{RAD}}}}}{{{{R}_{{CON}}} + {{R}_{{RAD}}}}} \to {{\tilde {T}}_{L}}.$
Идея линеаризации заключается в том, что для эффективно работающих ХИ абсолютная температура теплоносителя близка к абсолютной температуре конструкции, причем не только трубок, но и ребер. В [16] показано, что в случае “термически коротких” ребер линеаризация уравнения излучающего теплопроводящего ребра работает с высокой точностью. Однако, как будет показано ниже, в диапазоне температур 400–700 К для наиболее предпочтительных по массовому совершенству конструкций типового элемента ХИ перспективных КА погрешности линеаризации могут достигать 10% и более. Проблеме корректности линеаризации в настоящей работе будет уделено большое внимание. В результате будет предложена упрощенная аналитическая модель, дающая погрешность по сбрасываемому тепловому потоку менее 1% по сравнению с численным решением не линеаризованных уравнений, применимая в широком диапазоне интересующих параметров.
ТЕПЛОВОЕ СОСТОЯНИЕ РЕБРА
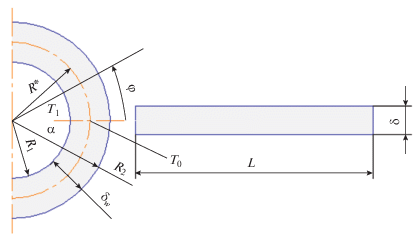
Рассмотрим стационарную одномерную задачу о распределении температуры по ребру постоянной толщиной $\delta $ и шириной $L.$ Температура ребра в месте контакта с трубкой (на торце $x = 0$) равна ${{T}_{0}},$ противоположный торец ребра ($x = L$) будем считать теплоизолированным. Используя приближение термически тонкой стенки, и предполагая, что ребро излучает с двух сторон, запишем уравнение теплопроводного излучающего ребра и граничные условия для него в виде:
(4)
${{\left. T \right|}_{{x = 0}}} = {{T}_{0}},\,\,\,\,{{\left. {\frac{{dT}}{{dx}}} \right|}_{{x = L}}} = 0,$Введем безразмерные переменные:
(5)
$y = \frac{x}{\mu },\,\,\,\,\mu = {{\left( {\frac{{\lambda \delta }}{{2\varepsilon \sigma T_{0}^{3}}}} \right)}^{{\frac{1}{2}}}},\,\,\,\,{{Н}_{0}} = \frac{L}{\mu },\,\,\,\,\tau = \frac{T}{{{{T}_{0}}}}.$Тогда задача (3), (4) принимает следующий безразмерный вид:
(7)
${{\left. \tau \right|}_{{y = 0}}} = 1,\,\,\,\,{{\left. {\frac{{d\tau }}{{dy}}} \right|}_{{y = {{H}_{0}}}}} = 0.$Задачу будем рассматривать в рамках асимптотики коротких ребер [16], предполагающей, что абсолютная температура ребра мало отличается от температуры на его горячем торце. Тогда
(8)
$\frac{{{{T}_{0}} - T}}{{{{T}_{0}}}} = 1 - \tau = \psi \ll 1,\,\,\,\,{{\tau }^{4}} \approx 1 - 4\psi .$Подставляя (8) в (6), (7), получим:
(10)
${{\left. \psi \right|}_{{y = 0}}} = 0,\,\,\,\,{{\left. {\frac{{d\psi }}{{dy}}} \right|}_{{y = {{H}_{0}}}}} = 0.$Задача (9), (10) имеет следующее точное решение:
(11)
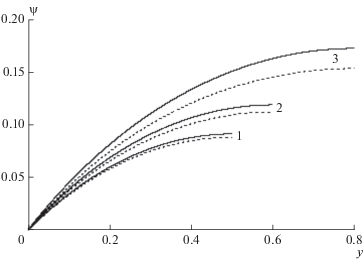
$\psi = \frac{1}{4}\left( {1 - \frac{{{{e}^{{2y}}}{{e}^{{ - 2{{H}_{0}}}}} + {{e}^{{ - 2y}}}{{e}^{{2{{H}_{0}}}}}}}{{{{e}^{{ - 2{{H}_{0}}}}} + {{e}^{{2{{H}_{0}}}}}}}} \right).$Рис. 2.
Распределения по длине ребра функции $\psi $, полученные из численного решения задачи (6), (7), и асимптотические решения (штриховые линии) по формуле (11): 1 – ${{Н}_{0}}$ = 0.5; 2 – 0.6; 3 – 0.8.
Для дальнейших рассуждений интересует, прежде всего, не само распределение температуры, а сбрасываемый тепловой поток (на единицу длины вдоль ребра). Для него можно записать выражение:
(12)
${{Q}_{R}} = - \lambda \delta {{\left. {\frac{{dT}}{{dx}}} \right|}_{{x = 0}}} = - \frac{{\lambda \delta {{T}_{0}}}}{\mu }{{\left. {\frac{{d\tau }}{{dy}}} \right|}_{{y = 0}}}\frac{{{{H}_{0}}}}{{{{H}_{0}}}} = \frac{{\lambda \delta {{T}_{0}}L}}{{{{\mu }^{2}}}}\left( {\frac{{ - 1}}{{{{H}_{0}}}}{{{\left. {\frac{{d\tau }}{{dy}}} \right|}}_{{y = 0}}}} \right) = 2\varepsilon \sigma T_{0}^{4}L\left( {\frac{{ - 1}}{{{{H}_{0}}}}{{{\left. {\frac{{d\tau }}{{dy}}} \right|}}_{{y = 0}}}} \right),$(13)
${{F}_{0}} = - \frac{1}{{{{H}_{0}}}}{{\left. {\frac{{d\tau }}{{dy}}} \right|}_{{y = 0}}} = - \frac{1}{{{{H}_{0}}}}{{\left. {\frac{{d(1 - \psi )}}{{dy}}} \right|}_{{y = 0}}} = \frac{{{\text{th}}(2{{H}_{0}})}}{{2{{H}_{0}}}}.$Отметим, что эффективность ребра зависит от единственного параметра – безразмерной ширины ребра. На рисунке 3 приведена эффективность ребра, рассчитанная по асимптотической формуле (13) и из численного решения задачи (6), (7). При ${{Н}_{0}} \leqslant 0.3$ асимптотическая формула дает погрешность менее 1%, при ${{Н}_{0}}$ = 0.8 относительная погрешность составляет 6.8%, при ${{Н}_{0}}$ = 1.5 погрешность составляет около 15%. Решение линеаризованной задачи занижает эффективность ребра по сравнению с численным решением не линеаризованного уравнения. Для вычисления эффективности ребра целесообразно вместо формулы (13) применять скорректированную формулу (14):
(14)
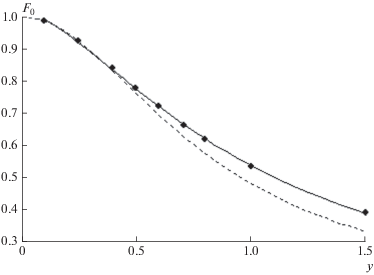
${{F}_{0}} = \frac{{{\text{2th}}\left( {{{H}_{0}}\left( {a - b{{H}_{0}}} \right)} \right)}}{{3{{H}_{0}}}},$Рис. 3.
Тепловая эффективность ребра в зависимости от его безразмерной ширины, полученная из численного решения задачи (6), (7) – точки; асимптотическое решение по формуле (13) – штриховая кривая; и рассчитанная по скорректированной формуле (14) – сплошная кривая.
ТЕПЛОВОЕ СОСТОЯНИЕ СТЕНКИ ТРУБОПРОВОДА
Рассмотрим в некотором поперечном сечении z элемент стенки трубы, начинающийся в месте стыковки ребра и трубопровода, где температура равна ${{T}_{0}},$ и заканчивающийся в плоскости симметрии между двумя соседними ребрами (рис. 4). Введены обозначения: ${{T}_{L}}$ – температура теплоносителя в данном сечении; $\alpha $ – коэффициент теплоотдачи в данном сечении (считаем его заданным).
Запишем уравнение теплопроводности в цилиндрической системе координат для элемента трубы:
(15)
$\frac{\partial }{{\partial r}}\left( {r\frac{{\partial T}}{{\partial r}}} \right) + \frac{1}{r}\frac{{{{\partial }^{2}}T}}{{\partial {{\varphi }^{2}}}} = 0.$Проинтегрируем (15) по $r$ от ${{R}_{1}}$ до ${{R}_{2}}$ и умножим на ${{\lambda }_{W}}$ – теплопроводность материала трубы:
(16)
${{\lambda }_{W}}{{R}_{2}}{{\left. {\frac{{\partial T}}{{\partial r}}} \right|}_{{r = {{R}_{2}}}}} - {{\lambda }_{W}}{{R}_{1}}{{\left. {\frac{{\partial T}}{{\partial r}}} \right|}_{{r = {{R}_{1}}}}} + {{\lambda }_{W}}\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {\frac{1}{r}\frac{{{{\partial }^{2}}T}}{{\partial {{\varphi }^{2}}}}dr} = 0.$Удельный тепловой поток, излучаемый внешней поверхностью трубы:
(17)
${{q}_{W}} = {{\varepsilon }_{W}}\sigma {{\left. {{{T}^{4}}} \right|}_{{r = {{R}_{2}}}}} = - {{\lambda }_{W}}{{R}_{2}}{{\left. {\frac{{\partial T}}{{\partial r}}} \right|}_{{r = {{R}_{2}}}}}.$Удельный тепловой поток от теплоносителя к внутренней поверхности трубы:
(18)
${{q}_{\alpha }} = \alpha \left( {{{T}_{L}} - {{{\left. T \right|}}_{{r = {{R}_{1}}}}}} \right) = - {{\lambda }_{W}}{{R}_{1}}{{\left. {\frac{{\partial T}}{{\partial r}}} \right|}_{{r = {{R}_{1}}}}}.$Тогда (15) запишется в виде:
(19)
${{\lambda }_{W}}\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {\frac{1}{r}} \frac{{{{\partial }^{2}}T}}{{\partial {{\varphi }^{2}}}}dr + {{R}_{1}}\alpha \left( {{{T}_{L}} - {{{\left. T \right|}}_{{r = {{R}_{1}}}}}} \right) = {{R}_{2}}{{\varepsilon }_{W}}\sigma {{\left. {{{T}^{4}}} \right|}_{{r = {{R}_{2}}}}}.$Теперь пренебрежем изменением температуры поперек стенки трубы (приближение термически тонкой стенки), т.е. будем считать, что $T = T\left( \varphi \right).$ Тогда (19) можно записать в виде:
(20)
${{\lambda }_{W}}\frac{{{{d}^{2}}T}}{{d{{\varphi }^{2}}}}\int\limits_{{{R}_{1}}}^{{{R}_{2}}} {\frac{1}{r}} dr + {{R}_{1}}\alpha \left( {{{T}_{L}} - T} \right) = {{R}_{2}}{{\varepsilon }_{W}}\sigma {{T}^{4}}.$Далее $\int_{{{R}_{1}}}^{{{R}_{2}}} {\frac{1}{r}dr} $ = $\ln {{R}_{2}} - \ln {{R}_{1}}$ = $\ln \frac{{{{R}_{2}}}}{{{{R}_{*}}}} - \ln \frac{{{{R}_{1}}}}{{{{R}_{*}}}}$ = $\ln \left( {1 + \frac{{{{\delta }_{W}}}}{{2{{R}_{*}}}}} \right) - \ln \left( {1 - \frac{{{{\delta }_{W}}}}{{2{{R}_{*}}}}} \right) \approx \frac{{{{\delta }_{W}}}}{{{{R}_{*}}}}.$
Последнее получено в предположении, что стенка тонкая, с точностью до членов третьего порядка малости по ${{{{\delta }_{W}}} \mathord{\left/ {\vphantom {{{{\delta }_{W}}} {(2{{R}_{*}})}}} \right. \kern-0em} {(2{{R}_{*}})}}.$ В результате уравнение (20) принимает вид:
(21)
${{\lambda }_{W}}{{\delta }_{W}}\frac{{{{d}^{2}}T}}{{dx_{W}^{2}}} + \frac{{{{R}_{1}}}}{{{{R}_{*}}}}\alpha \left( {{{T}_{L}} - T} \right) = \frac{{{{R}_{2}}}}{{{{R}_{*}}}}{{\varepsilon }_{W}}\sigma {{T}^{4}}.$Граничные условия для уравнения (21):
(22)
${{\left. T \right|}_{{{{x}_{W}} = 0}}} = {{T}_{0}},\,\,\,\,{{\left. {\frac{{dT}}{{d{{x}_{W}}}}} \right|}_{{{{x}_{W}} = l}}} = 0,\,\,\,\,l = \frac{{\pi {{R}_{*}}}}{2}.$Обозначим отклонение температуры стенки трубы от температуры теплоносителя ${{\left( {{{T}_{L}} - T} \right)} \mathord{\left/ {\vphantom {{\left( {{{T}_{L}} - T} \right)} {{{T}_{L}}}}} \right. \kern-0em} {{{T}_{L}}}} = \theta ;$ $T = {{T}_{L}}\left( {1 - \theta } \right),$ тогда уравнение (21) примет вид:
(23)
$\frac{{{{\lambda }_{W}}{{\delta }_{W}}{{R}_{*}}}}{{{{R}_{2}}{{\varepsilon }_{W}}\sigma T_{L}^{3}}}\frac{{{{d}^{2}}\theta }}{{dx_{W}^{2}}} = \frac{{{{R}_{1}}\alpha }}{{{{R}_{2}}{{\varepsilon }_{W}}\sigma T_{L}^{3}}}\theta - {{\left( {1 - \theta } \right)}^{4}}.$Введем безразмерные обозначения
(24)
$\frac{{{{\lambda }_{W}}{{\delta }_{W}}{{R}_{*}}}}{{{{R}_{2}}{{\varepsilon }_{W}}\sigma T_{L}^{3}{{l}^{2}}}} = \gamma ;\,\,\,\,\frac{{{{R}_{1}}\alpha }}{{{{R}_{2}}{{\varepsilon }_{W}}\sigma T_{L}^{3}}} = \beta - 4;\,\,\,\,{{y}_{W}} = \frac{{{{x}_{W}}}}{{{{\mu }_{W}}}}.$Отметим, что безразмерный параметр $\beta $ не зависит от коэффициента теплопроводности материала, а параметр $\gamma $ не зависит от коэффициента теплоотдачи. Уравнение (23) преобразуется:
(25)
${{l}^{2}}\frac{\gamma }{{\mu _{W}^{2}}}\frac{{{{d}^{2}}\theta }}{{dy_{W}^{2}}} = \left( {\beta - 4} \right)\theta - {{\left( {1 - \theta } \right)}^{4}}.$Теперь в качестве пространственного масштаба выберем ${{\mu }_{W}} = l\sqrt {{\gamma \mathord{\left/ {\vphantom {\gamma \beta }} \right. \kern-0em} \beta }} .$ Получим безразмерное уравнение теплового состояния элемента стенки трубы и граничные условия для него:
(26)
$\frac{{{{d}^{2}}\theta }}{{dy_{W}^{2}}} = \frac{{\beta - 4}}{\beta }\theta - \frac{{{{{\left( {1 - \theta } \right)}}^{4}}}}{\beta }.$(27)
${{\left. \theta \right|}_{{{{y}_{W}} = 0}}} = \frac{{{{T}_{L}} - {{T}_{0}}}}{{{{T}_{L}}}} = {{\theta }_{0}};\,\,\,\,{{\left. {\frac{{d\theta }}{{d{{y}_{W}}}}} \right|}_{{{{y}_{W}} = h}}} = 0;\,\,\,\,h = \frac{l}{{{{\mu }_{W}}}} = \sqrt {\frac{\beta }{\gamma }} .$Будем рассматривать случай, когда температура стенки трубы мало отличается от температуры теплоносителя ($\theta \ll 1$). Тогда ${{\left( {1 - \theta } \right)}^{4}} \approx 1 - 4\theta .$ Уравнение (26) линеаризуется:
Точное решение уравнения (28) с граничными условиями (27):
(29)
$\theta = \left( {{{\theta }_{0}} - \frac{1}{\beta }} \right)\frac{{{{e}^{{ - h}}}{{e}^{y}} + {{e}^{h}}{{e}^{{ - y}}}}}{{{{e}^{{ - h}}} + {{e}^{h}}}} + \frac{1}{\beta }.$Отметим, что численное решение уравнения (26) совпадает с распределением (29) с погрешность менее 1% для $\beta \geqslant 100$ и $h \leqslant 1.5,$ которые являются типичными для ХИ. На рисунке 5 численное решение (26) сравнивается с распределением (29) для $\beta = 20.$ Видно, что даже в этом случае решения достаточно близки.
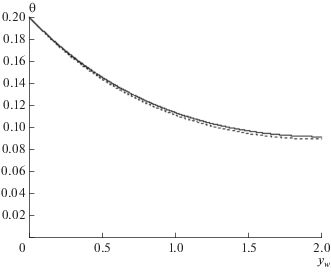
Рис. 5.
Численное решение (26) – сплошная кривая и распределение (29) – штриховая кривая для $\beta = 20,$ ${{\theta }_{0}} = 0.2.$
Из (29) можно получить аналитическое выражение для теплового потока (на единицу длины вдоль трубы), поступающего в ребро из рассматриваемого элемента стенки трубы ${{Q}_{{WR}}},$ выражение для полного теплового потока, получаемого от теплоносителя $Q,$ и выражение для теплового потока, излучаемого элементом стенки трубы ${{Q}_{W}}{\text{:}}$
(30)
${{Q}_{{WR}}} = - {{\lambda }_{W}}{{\delta }_{W}}{{\left. {\frac{{dT}}{{dx}}} \right|}_{{x = 0}}} = - \frac{{{{\lambda }_{W}}{{\delta }_{W}}{{T}_{L}}}}{{{{\mu }_{W}}}}{{\left. {\frac{{d\theta }}{{dy}}} \right|}_{{y = 0}}} = Q_{W}^{{{\text{MAX}}}}\left( { - \frac{\beta }{h}{{{\left. {\frac{{d\theta }}{{dy}}} \right|}}_{{y = 0}}}} \right) = Q_{W}^{{{\text{MAX}}}}\left( {\beta {{\theta }_{0}} - 1} \right)\frac{{{\text{th}}\left( h \right)}}{h};$(31)
$\begin{gathered} Q = \frac{{{{R}_{1}}}}{{{{R}_{*}}}}\int\limits_0^l {\alpha \left( {{{T}_{L}} - T} \right)dx} = \frac{{{{R}_{1}}}}{{{{R}_{*}}}}\alpha {{T}_{L}}{{\mu }_{W}}\int\limits_0^h {\theta dy} = Q_{W}^{{{\text{MAX}}}}\left( {\frac{{\left( {\beta - 4} \right)}}{h}\int\limits_0^h {\theta dy} } \right) = \\ = Q_{W}^{{{\text{MAX}}}}\left( {\left( {\beta - 4} \right)\left( {{{\theta }_{0}} - \frac{1}{\beta }} \right)\frac{{{\text{th}}\left( h \right)}}{h} + \frac{{\beta - 4}}{\beta }} \right); \\ \end{gathered} $(32)
${{Q}_{W}} = Q - {{Q}_{{WR}}} = Q_{W}^{{{\text{MAX}}}}\left( {1 - 4\left( {{{\theta }_{0}} - \frac{1}{\beta }} \right)\frac{{{\text{th}}\left( h \right)}}{h} - \frac{4}{\beta }} \right);$СОПРЯЖЕНИЕ НА ГРАНИЦЕ СТЕНКИ ТРУБЫ И ТОРЦА РЕБРА
Получено, что тепловой поток, отдаваемый ребром, зависит от температуры корня ребра по (12), (14). Температура корня ребра определяется выражением ${{T}_{0}} = {{T}_{L}}\left( {1 - {{\theta }_{0}}} \right),$ где ${{\theta }_{0}}$ – малая величина. Учитывая последнее обстоятельство, формулу для теплового потока от ребра можно выразить через температуру теплоносителя:
где $Q_{R}^{{{\text{MAX}}}} = 2\varepsilon \sigma T_{L}^{4}L$ – максимально возможный тепловой поток с ребра, если бы его температура равнялась температуре теплоносителя;$F = \frac{{2{\text{th}}\left( {H\left( {a - bH} \right)} \right)}}{{3H}}$ – эффективность ребра;
$H = L{{\left( {\frac{{2\varepsilon \sigma T_{L}^{3}}}{{\lambda \delta }}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – безразмерная ширина ребра, в которой фигурирует не температура основания ребра, а температура теплоносителя;
$k = \frac{5}{2} + \frac{{3H\left( {a - 2bH} \right)}}{{{\text{sh}}\left( {2H\left( {a - bH} \right)} \right)}}$ – коэффициент, учитывающий, что температура корня ребра отличается от температуры теплоносителя. Отметим, что $k \to 4$ при $H \to 0$ и убывает по мере возрастания $H.$
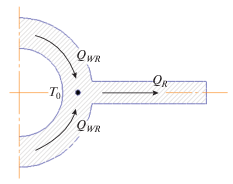
Будем считать, что тепло, поступающее в ребро в месте его сопряжения с трубопроводом, равно сумме тепловых потоков ${{Q}_{{WR}}}$ с двух смежных участков трубы (рис. 6), т.е.
Выражение (30) для ${{Q}_{{WR}}}$ можно представить в форме аналогичной (33):
где $f = {{{\text{th}}(h)} \mathord{\left/ {\vphantom {{{\text{th}}(h)} h}} \right. \kern-0em} h}$ – аналог коэффициента эффективности ребра, но только для элемента трубы.Из (34) найдем ${{\theta }_{0}}{\text{:}}$
(36)
${{\theta }_{0}} = \frac{1}{\beta }\frac{{B\phi + 1}}{{B\phi + {k \mathord{\left/ {\vphantom {k \beta }} \right. \kern-0em} \beta }}},$Теперь подставим ${{\theta }_{0}}$ в выражения (33) и (32):
(37)
${{Q}_{R}} = Q_{R}^{{{\text{MAX}}}}F\left( {1 - k\frac{{B\phi + 1}}{{B\phi \beta + k}}} \right) = Q_{R}^{{{\text{MAX}}}}FB\phi \frac{{\beta - k}}{{B\phi \beta + k}} = 2Q_{W}^{{{\text{MAX}}}}f\frac{{\beta - k}}{{B\phi \beta + k}},$(38)
$2{{Q}_{W}} = 2Q_{W}^{{{\text{MAX}}}}\left( {1 - 4f\left( {{{\theta }_{0}} - \frac{1}{\beta }} \right) - \frac{4}{\beta }} \right) = 2Q_{W}^{{{\text{MAX}}}}\left( {1 - \frac{{4f}}{\beta }\frac{{\beta - k}}{{B\phi \beta + k}} - \frac{4}{\beta }} \right).$В выражении (38) заменим $\frac{{\beta - k}}{{B\phi \beta + k}}$ на $\frac{{{{Q}_{R}}}}{{2Q_{W}^{{{\text{MAX}}}}f}},$ тогда
(39)
$2{{Q}_{W}} = 2Q_{W}^{{{\text{MAX}}}}\left( {1 - {4 \mathord{\left/ {\vphantom {4 \beta }} \right. \kern-0em} \beta }} \right) - {{4{{Q}_{R}}} \mathord{\left/ {\vphantom {{4{{Q}_{R}}} \beta }} \right. \kern-0em} \beta }.$Общий тепловой поток с ребра и двух элементов стенки трубы:
(40)
$Q = 2{{Q}_{W}} + {{Q}_{R}} = \left( {1 - {4 \mathord{\left/ {\vphantom {4 \beta }} \right. \kern-0em} \beta }} \right)\left( {2Q_{W}^{{{\text{MAX}}}} + {{Q}_{R}}} \right).$Формулы (37) и (40) представляют собой упрощенную аналитическую модель для вычисления теплового потока с ребра и общего теплового потока с ребра и двух элементов стенки трубы в некотором сечении.
ПРОВЕРКА УПРОЩЕННОЙ АНАЛИТИЧЕСКОЙ МОДЕЛИ
Сопоставим результаты упрощенной модели с результатами совместного численного решения нелинеаризованных уравнений (6) и (26) для типового элемента холодильника-излучателя из алюминиевого сплава (табл. 1). В работе [12] ставился вопрос о выборе теплоносителя для панельных излучателей мегаваттного уровня мощности. Там в качестве оптимального теплоносителя была рекомендована дифенильная смесь. Примерные средние значения свойств этого теплоносителя, а также коэффициента теплоотдачи примем согласно [12].
Таблица 1.
Параметры типового холодильника-излучателя
| Параметр | Значение |
|---|---|
| Теплопроводность материала ребра и трубки, $\lambda ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\lambda }_{W}}$, Вт/(К м) | 120 |
| Плотность материала ребра и трубки, $\rho ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rho }_{W}}$, кг/м3 | 2790 |
| Плотность теплоносителя, ${{\rho }_{L}}$, кг/м3 | 900 |
| Теплоемкость теплоносителя, $c$, Дж/(кг К) | 2300 |
| Излучательная способность поверхности ребра и трубки, $\varepsilon ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\varepsilon }_{W}}$ | 0.9 |
| Коэффициент теплоотдачи, ${{\alpha }}$ Вт/(К м2) | 2000 |
Зададим следующие типичные для ХИ геометрические параметры: средний радиус трубки ${{R}_{*}}$ = 5.5 мм; толщина стенки трубки ${{\delta }_{W}}$ = 1 мм (${{R}_{1}}$ = 5 мм; ${{R}_{2}}$ = 6 мм); ширина ребра $L$ = 40 мм; толщина ребра $\delta $ = 0.25 мм.
Для данных условий в табл. 2 приведена температура сопряжения ${{T}_{0}}$ ребра и трубы, тепловой поток с ребра ${{Q}_{R}}$ и полный тепловой поток $Q$ (на единицу длины) для некоторого сечения при температуре теплоносителя ${{T}_{L}}$ = 400; 550 и 700 К.
Таблица 2.
Численное решение и решение по приближенной модели для сечения типового элемента ХИ с заданной температурой
| ${{T}_{L}}$,К | ${{T}_{0}}$, К | ${{Q}_{R}}$, Вт/м | $Q$, Вт/м | |||||
|---|---|---|---|---|---|---|---|---|
| числ. решение | упрощ. модель |
числ. решение | упрощ. модель |
погрешн., % |
числ. решение | упрощ. модель |
погрешн., % |
|
| 400 | 396.1 | 395.8 | 73.48 | 73.21 | –0.37 | 97.33 | 97.07 | –0.26 |
| 550 | 539.0 | 538.3 | 194.26 | 194.48 | 0.12 | 276.96 | 276.85 | –0.04 |
| 700 | 677.2 | 675.9 | 376.22 | 374.38 | –0.49 | 584.01 | 580.90 | –0.53 |
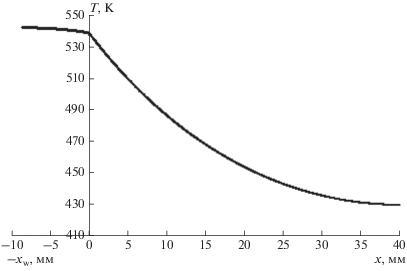
Видно, что результаты упрощенной модели с высокой точностью (с погрешностью менее 1%) совпадают с результатами совместного решения нелинеаризованных уравнений для рассмотренных случаев. Рисунок 7 иллюстрирует распределение температуры по трубе и по ребру при температуре теплоносителя 550 К (численное решение).
Чтобы получить распределение температуры вдоль всего трубопровода ХИ (вдоль координаты z), запишем уравнение энергии в виде:
где $G$и $c$ – массовый расход и удельная теплоемкость теплоносителя.Интегрируя (41) по координате $z$ с краевым условием ${{\left. {{{T}_{L}}} \right|}_{{z = 0}}} = {{T}_{{L0}}}$, можно рассчитать изменение температуры теплоносителя вдоль трубы, а также расстояние $Z$, на котором теплоноситель остынет до требуемой температуры и сбросит в космическое пространство требуемое количество тепла. Численное решение уравнения (41) не представляет каких-либо сложностей, поскольку для этого существуют эффективные методы [19]. Таким образом, упрощенная математическая модель (37), (40), (41) позволяет легко рассчитать тепловое состояние всего холодильника-излучателя. С другой стороны, аналитический вид выражений для тепловых потоков (37), (40) позволяет перейти к анализу общих закономерностей функционирования ХИ. В данной работе рассмотрим вопрос о выборе оптимальных параметров оребрения холодильника-излучателя.
ЗАДАЧА ПОИСКА ОПТИМАЛЬНЫХ ПАРАМЕТРОВ ОРЕБРЕНИЯ
В качестве параметра, характеризующего массовое совершенство конструкции, выберем общий удельный тепловой поток (на единицу длины) $Q$ от холодильника-излучателя в некотором сечении, отнесенный к удельной (на единицу длины) массе $M{\text{:}}$
Параметр $\Phi $ можно назвать удельной (по длине) массовой эффективностью холодильника-излучателя. Удельная масса включает в себя удельную массу ребра ${{M}_{R}} = \delta L\rho ,$ массу трубки и теплоносителя в трубке:
(42)
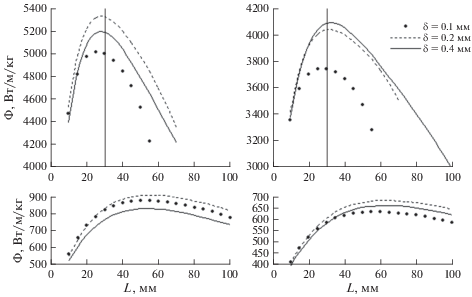
$M = \delta L\rho + \pi \left( {{{R}_{*}}{{\delta }_{W}}\rho + {{R_{1}^{2}{{\rho }_{L}}} \mathord{\left/ {\vphantom {{R_{1}^{2}{{\rho }_{L}}} 2}} \right. \kern-0em} 2}} \right).$Рис. 8.
Удельная массовая эффективность излучателя $\Phi = {Q \mathord{\left/ {\vphantom {Q M}} \right. \kern-0em} M}$ при различной ширине ребра и температурах 700 К (сверху) и 400 К (снизу); толщина стенки трубки ${{\delta }_{W}}$ = 1омм; средний радиус трубки ${{R}_{*}}$ = 5.5 мм (слева) 7.5 мм (справа).
Из рисунка следует:
1. При более высокой температуре максимум функции $\Phi $ наблюдается при меньших значениях ширины ребра: при 700 К – ${{L}_{{OPT}}}$ ≈ 30 мм; при 400 К – ${{L}_{{OPT}}}$ ≈ 50–60 мм.
2. Для случая ${{R}_{*}}$ = 5.5 мм предпочтительной толщиной ребра является толщина $\delta $ = = 0.2 мм. Для случая ${{R}_{*}}$ = 7.5 мм предпочтительная толщина ребра при 700 К – это $\delta $ = = 0.4 мм, а при 400 К – это $\delta $ = 0.2 мм.
3. При увеличении радиуса трубки максимум $\Phi $ несколько смещается вправо – в сторону более длинных ребер.
Таким образом, существует максимум функции $\Phi $ при оптимальной ширине ${{L}_{{ОPТ}}}$ и толщине ребра ${{\delta }_{{ОPТ}}},$ которые зависят от температуры теплоносителя. Кроме того, оптимальная ширина и толщина ребра тем больше, чем больше радиус трубки.
Оптимальную ширину и толщину ребра будем искать из решения системы:
По правилам дифференцирования $\left( {\frac{Q}{M}} \right){\kern 1pt} ' = \frac{{Q{\kern 1pt} 'M - QM{\kern 1pt} '}}{{{{M}^{2}}}}.$ Тогда уравнение $\left( {\frac{Q}{M}} \right){\kern 1pt} ' = 0$ можно заменить на $Q{\kern 1pt} ' = Q\frac{{M{\kern 1pt} '}}{M}.$ С учетом того, что в выражении (40) $\beta $ и $Q_{W}^{{{\text{MAX}}}}$ не зависят от параметров оребрения, система (43) принимает вид:
(44)
$\left\{ \begin{gathered} \frac{{d{{Q}_{R}}}}{{dL}} = \left( {{{Q}_{R}} + 2Q_{W}^{{\max }}} \right)\frac{1}{M}\frac{{dM}}{{dL}}; \hfill \\ \frac{{d{{Q}_{R}}}}{{d\delta }} = \left( {{{Q}_{R}} + 2Q_{W}^{{\max }}} \right)\frac{1}{M}\frac{{dM}}{{d\delta }}. \hfill \\ \end{gathered} \right\}$В выражении (33) для теплового потока с ребра поправка $k{{\theta }_{0}}$ ~ ${{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} \beta }} \right. \kern-0em} \beta }$ является малой величиной. Для практически важных случаев коэффициент конвективной теплоотдачи и параметр $\beta $ очень высок. Поэтому примем
Далее:
Тогда система (44) преобразуется к виду:
(46)
$\left\{ \begin{gathered} \frac{2}{3}\left( {1 - {\text{t}}{{{\text{h}}}^{2}}\left[ {H\left( {a - bH} \right)} \right]} \right)\left( {a - 2bH} \right) = \left( {F + B} \right)\frac{{\rho \delta L}}{M}; \hfill \\ \frac{{{\text{th}}\left[ {H\left( {a - bH} \right)} \right]}}{{3H}} - \frac{1}{3}\left( {1 - {\text{t}}{{{\text{h}}}^{2}}\left[ {H\left( {a - bH} \right)} \right]} \right)\left( {a - 2bH} \right) = \left( {F + B} \right)\frac{{\rho \delta L}}{M}. \hfill \\ \end{gathered} \right\}$Левые части уравнений системы (46) зависят только от $H,$ а правые – одинаковые. Приравнивая левые части уравнений системы (46), можно получить безразмерную ширину ребра оптимального по массе холодильника-излучателя:
которая при больших значениях $\alpha $ имеет единственное универсальное значение.Отметим, что эффективность ребра оптимального по массе холодильника-излучателя ${{F}_{{ОPТ}}}$ = 0.5646. Далее выразим ${{\delta }_{{ОPТ}}}$ через ${{H}_{{ОPТ}}}$ и подставим, например, в 1-е уравнение системы (46):
(47)
${{\delta }_{{ОPТ}}} = \frac{{2\varepsilon \sigma T_{L}^{3}}}{\lambda }{{\left( {\frac{{{{L}_{{ОPТ}}}}}{{{{H}_{{ОPТ}}}}}} \right)}^{2}},$(48)
$\left( {1 + \left( {\frac{{{{R}_{*}}{{\delta }_{W}}{{\rho }_{W}}}}{\rho } + \frac{{R_{1}^{2}{{\rho }_{L}}}}{{2\rho }}} \right)\frac{{\pi \lambda H_{{ОPТ}}^{2}}}{{2\varepsilon \sigma T_{L}^{3}L_{{ОPТ}}^{3}}}} \right){{C}_{{ОPТ}}} = {{F}_{{ОPТ}}} + \frac{{{{\varepsilon }_{W}}\pi {{R}_{2}}}}{{2\varepsilon {{L}_{{ОPТ}}}}},$Считая ${{\varepsilon }_{W}} = \varepsilon ,$ в уравнение (48) вместо $L_{{ОPТ}}^{{}}$ можно ввести безразмерную величину $\Lambda = \frac{{2L_{{ОPТ}}^{{}}}}{{\pi {{R}_{2}}}}$ $\left( {\Lambda = \frac{1}{{{{B}_{{OPT}}}}}} \right),$ что приведет его к следующему безразмерному виду:
(49)
$\left( {1 + \frac{A}{{{{\Lambda }^{3}}}}} \right){{C}_{{ОPТ}}} = {{F}_{{ОPТ}}} + \frac{1}{\Lambda },$Рис. 9.
Универсальная безразмерная зависимость $\Lambda \left( A \right)$ для вычисления оптимальной ширины ребра.
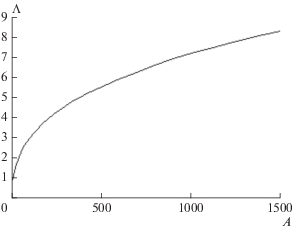
По решению (49) и формуле (47) легко получить размерные значения оптимальной ширины и толщины ребра для условий табл. 1. На рисунках 10 и 11 приведена оптимальная ширина и толщина ребра в температурном диапазоне от 300 до 700 К для ХИ с трубкой толщиной ${{\delta }_{W}}$ = 1 мм и наружным радиусом трубки ${{R}_{2}}$ = 4 мм; ${{R}_{2}}$ = 6 мм; ${{R}_{2}}$ = = 8 мм. При высокой температуре оптимальная ширина ребра составляет ориентировочно около 30 мм, при низкой – примерно в 2.5 раза больше. Если при 300 К оптимальная толщина ребра 0.1 мм, то при 700 К – примерно в 2 раза больше. Оптимальная толщина ребра оказалась почти пропорциональна радиусу трубки.
Рис. 10.
Оптимальная ширина ребра в зависимости от температуры теплоносителя. Наружный радиус трубки 4, 6, 8 мм, толщина стенки трубки 1 мм.
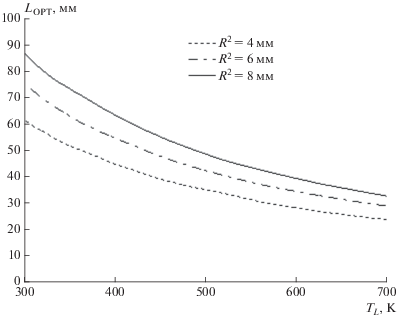
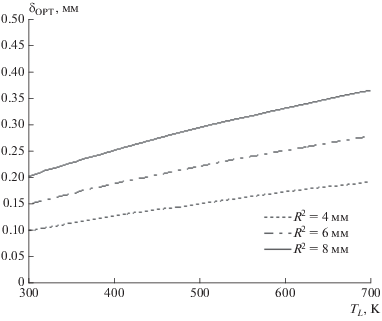
Рис. 11.
Оптимальная толщина ребра в зависимости от температуры теплоносителя. Наружный радиус трубки 4, 6, 8 мм, толщина стенки трубки 1 мм.
Рисунки 12 и 13 иллюстрируют влияние толщины стенки трубки при ее наружном радиусе ${{R}_{2}}$ = 6 мм.
Рис. 12.
Оптимальная ширина ребра в зависимости от температуры теплоносителя. Наружный радиус трубки 6 мм, толщина стенки трубки 0.5; 1 и 2 мм.
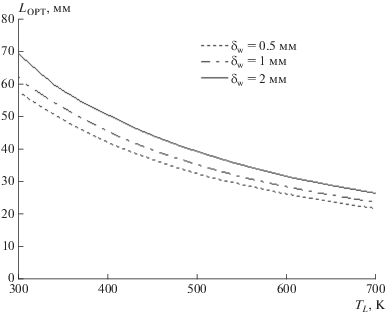
Рис. 13.
Оптимальная толщина ребра в зависимости от температуры теплоносителя. Наружный радиус трубки 6 мм, толщина стенки трубки 0.5; 1 и 2 мм.
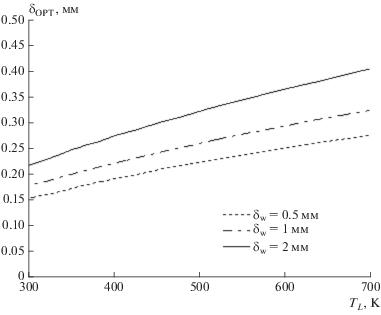
Таким образом, чем больше радиус и толщина стенки трубки, тем большее по ширине и толщине требуется ребро.
Полученные результаты объясняют поведение функции $\Phi = {Q \mathord{\left/ {\vphantom {Q M}} \right. \kern-0em} M}$ – удельной массовой эффективности холодильника-излучателя (рис. 8) и хорошо согласуются с результатами, полученными в работе [13] путем вычислительного эксперимента. Отметим, что в работе [13] учитывалось солнечное излучение.
Теперь рассмотрим задачу применительно к условиям, характерным для излучателей перспективных космических аппаратов с ядерной энергоустановкой на борту. Примем, что суммарная тепловая мощность, которую необходимо сбросить в космос ${{N}_{\Sigma }}$ = 1000 кВт, температура теплоносителя на входе ${{T}_{{L0}}}$ = 680 К и требуемая температура на выходе ${{T}_{{LZ}}}$ = 380 К. Коэффициент теплоотдачи, свойства материала ХИ и теплоносителя считаем постоянными (по табл. 1). Суммарный массовый расход теплоносителя (на все параллельные потоки) определяется выражением
Примем, что наружный радиус трубки ХИ ${{R}_{2}}$ = 6 мм, толщина стенки трубки ${{\delta }_{W}}$ = 1 мм, количество параллельных потоков $n$ = 20.
Проинтегрируем (41) по координате $z$ с краевым условием ${{\left. {{{T}_{L}}} \right|}_{{z = 0}}} = {{T}_{{L0}}}$ и определим расстояние $Z,$ на котором теплоноситель остынет до требуемой температуры. Будем рассматривать 5 вариантов с различными параметрами оребрения:
1) ширина и толщина ребра постоянны и соответствуют оптимальным значениям при температуре 680 К;
2) ширина и толщина ребра постоянны и соответствуют оптимальным значениям при температуре 380 К;
3) ширина и толщина ребра постоянны и соответствуют оптимальным значениям при среднеарифметической температуре 530 К;
4) ширина и толщина ребра, переменные по длине потока, вычисляются как оптимальные в зависимости от местной температуры теплоносителя (рис. 14);
Рис. 14.
Изменение температуры теплоносителя вдоль потока и соответствующая ей оптимальная ширина и толщина ребра (расчет № 4).
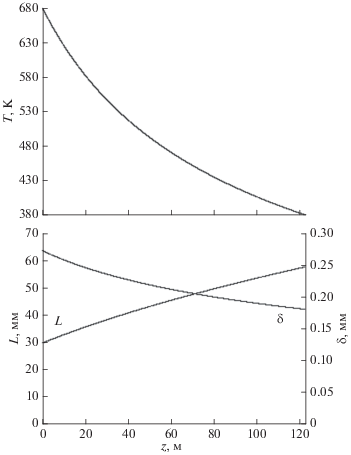
5) оптимальная ширина и толщина ребра, вычисляемые в расчете № 4, усреднены по длине потока.
Результаты расчетов представлены в табл. 3: Z – длина потока; $M$ – общая масса ХИ; ${{S}_{\Sigma }} = 2nZ\left( {2{{R}_{2}} + 2L} \right)$ – геометрическая излучающая поверхность ХИ (с двух сторон); ${{{{N}_{\Sigma }}} \mathord{\left/ {\vphantom {{{{N}_{\Sigma }}} M}} \right. \kern-0em} M}$ – удельная мощность по массе; ${M \mathord{\left/ {\vphantom {M {{{S}_{\Sigma }}}}} \right. \kern-0em} {{{S}_{\Sigma }}}}$ – удельная масса излучателя; доля излучения, отведенная ребрами ${{{{N}_{{R\Sigma }}}} \mathord{\left/ {\vphantom {{{{N}_{{R\Sigma }}}} {{{N}_{\Sigma }}}}} \right. \kern-0em} {{{N}_{\Sigma }}}};$ относительная масса оребрения ${{{{M}_{R}}} \mathord{\left/ {\vphantom {{{{M}_{R}}} M}} \right. \kern-0em} M}.$
Таблица 3.
Результаты расчета характеристик ХИ мощностью 1 МВт
| № | L, мм |
δ, мм |
Z, м |
$M$, кг |
$M - {{M}_{{\min }}}$, кг | ${{S}_{\Sigma }}$, м2 | $\frac{{{{N}_{\Sigma }}}}{{{{M}_{{}}}}},$ кВт/кг | $\frac{M}{{{{S}_{\Sigma }}}},$ кг/м2 | $\frac{{{{N}_{{R\Sigma }}}}}{{{{N}_{\Sigma }}}}$ | $\frac{{{{M}_{R}}}}{M}$ |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 29.74 | 0.273 | 136.0 | 578.1 | 35.1 | 389.0 | 1.73 | 1.49 | 0.69 | 0.21 |
| 2 | 57.87 | 0.181 | 123.8 | 558.1 | 15.1 | 632.5 | 1.79 | 0.88 | 0.70 | 0.26 |
| 3 | 39.74 | 0.231 | 126.3 | 551.5 | 8.5 | 462.1 | 1.81 | 1.19 | 0.70 | 0.23 |
| 4 | 123.2 | 543.0 | 0.0 | 504.1 | 1.84 | 1.08 | 0.71 | 0.24 | ||
| 5 | 45.17 | 0.216 | 123.8 | 548.4 | 5.4 | 506.6 | 1.82 | 1.08 | 0.71 | 0.25 |
Таким образом, проведенные расчеты применительно к условиям, характерным для излучателей перспективных космических аппаратов с мощностью 1 МВт (${{R}_{2}}$ = 6 мм, ${{\delta }_{W}}$ = = 1 мм), показывают, что при оптимальной ширине и толщине ребра суммарная масса оребрения составляет около четверти массы ХИ, при этом ребра сбрасывают около 70% тепла.
ВЫВОДЫ
Представлена уточненная методика приблизительного аналитического расчета холодильника-излучателя. Она предполагает расчет теплового состояния элемента трубы и ребра с последующим сопряжением решений. На основе полученных аналитических выражений для тепловых потоков от холодильника излучателя проведен поиск оптимальных по массе геометрических параметров ребра постоянной толщины. Получено, что, в практически важных случаях, когда коэффициент теплоотдачи высок, ребро оптимального по массе холодильника-излучателя имеет единственное значение безразмерной ширины и эффективности (около 60%). С другой стороны, получено, что чем больше наружный радиус и толщина стенки трубы, тем большее по ширине и толщине требуется ребро. Предложенная методика поиска оптимальных параметров оребрения применена к условиям, характерным для излучателей перспективных космических аппаратов с уровнем мощности 1 МВт.
Список литературы
Фаворский О.Н., Каданер Я.С. Вопросы теплообмена в космосе. М.: Высшая школа, 1967. 240 с.
Залетаев В.М., Капинос Ю.В., Сургучев О.В. Расчет теплообмена космического аппарата. М.: Машиностроение, 1979. 208 с.
Синявский В.В. Научно-технический задел по ядерному электроракетному межорбитальному буксиру “Геркулес” // Космическая техника и технологии. 2013. № 3. С. 25–45.
Гафаров А.А., Пришлецов А.Б., Рождественский Н.М. Сравнительный анализ транспортно-энергетических модулей на базе ядерных энергетических установок с системами прямого и динамического преобразования энергии // Межд. конф. “Ядерная энергетика в космосе – 2005". Материалы научно-технической конф. Т. 1. М., 2005. С. 101–104.
Андреев П.В., Богуш И.П., Зарицкий Г.А. Обоснование характеристик термоэмиссионных космических ЯЭУ второго поколения: проектные и экспериментальные результаты // V Международная конференция “Ядерная энергетика в космосе”. Сб. докладов. Ч. 1. Подольск, 1999.
Jansen F., Bauer W., Masson F., Ruault J.M., Worms J.C., Detsis E., Lassoudiere F., Granjon R., Gaia E., Ferraris S., Tosi M.C., Koroteev A. S., Semenkin A.V., Solodukhin A., Tinsley T., Hodgson Z., Guimaraes L.N.F. Step-by-step realization of the international nuclear power and propulsion system (INPPS) mission. Proceedings of 66th International Astronautical Congress 2015 (IAC 2015): Space – The Gateway for Mankind’s Future, IAF, 2015. P. 7716–7724.
Koroteev A.S., Oshev Y.A., Popov S.A., Karevsky A.V., Solodukhin A.Y., Zakharenkov L.E., Semenkin A.V. Nuclear power propulsion system for spacecraft // Thermal Engineering. 2015. V. 62. № 13. P. 971–980.
Романов А. В. Системы обеспечения тепловых режимов герметичных отсеков и ЯЭУ космических аппаратов. СПб.: АНО ЛА “Профессионал”, 2014. 248 с.
Chang H.V. Optimization of a heat pipe radiator design // American Institute of Aeronautics and Astronautics, Thermophysics Conference, 19th, Snowmass, CO. Palo Alto, CA. 1984.
Coskun S.B., Atay M.T. Analysis of Convective Straight and Radial Fins with Temperature-Dependent Thermal Conductivity Using Variational Iteration Method with Comparison with Respect to Finite Element Analysis. Mathematical Problems in Engineering, No. 1, 2007. P. 15.
Hosseini M.J., Gorji M., Ghanbarpour M. Solution of Temperature Distribution in a Radiating Fin Using Homotopy Perturbation Method. Mathematical Problems in Engineering, № 1. 2009. P. 8.
Расчетное сопоставление эффективности применения различных теплоносителей для панельных холодильников-излучателей космических аппаратов. / Волков Н.Н., Волкова Л.И., Григорьев А.Л., Ильмов Д.Н. [и др.] // Теплоэнергетика, 2018. № 11. С. 78–86.
Ильмов Д.Н., Мавров В.А. Оптимизация панельных теплообменников-излучателей космических энергоустановок // Тепловые процессы в технике. 2019. Т. 11. № 6. С. 265–274.
Ермолаева Ю.О., Ризаханов Р.Н., Сигалаев С.К. Аналитический расчет распределения температуры излучающей пластины. Известия РАН. Энергетика". № 5. 2012. С. 138–143.
Ермолаева Ю.О., Ризаханов Р.Н., Сигалаев С.К. Применение аналитических методов расчета распределения температуры излучающей пластины для решения задач обеспечения теплосброса с борта космического аппарата. Известия РАН. Энергетика", № 1. 2014. С. 135–140.
Черкасов С.Г. Асимптотические решения в задаче о теплопроводном излучающем ребре // Теплофизика высоких температур. 2011. Т. 49. № 6. С. 955–957.
Черкасов С.Г., Лаптев И.В. Приближенное аналитическое решение двухмерной задачи о теплопроводном излучающем ребре // Теплофизика высоких температур. 2017. Т. 55. № 1. С. 81–84.
Черкасов С.Г., Лаптев И.В. Приближенный метод расчета теплового режима панельного холодильника-излучателя // Тепловые процессы в технике. 2018. Т. 10. № 3–4. С. 116–124.
Формалев В.Ф., Ревизников Д.Л. Численные методы. М.: ФИЗМАТЛИТ, 2004. 400 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика