Известия РАН. Энергетика, 2021, № 4, стр. 24-41
Моделирование редких событий при расчете показателей балансовой надежности ЭЭС
В. П. Обоскалов 1, 2, *, А. С. Х. Абдель Менаем 2
1 НИЦ “Надежность и ресурс больших систем и машин” УрО РАН
Екатеринбург, Россия
2 Уральский федеральный университет
Екатеринбург, Россия
* E-mail: vpo1704@mail.ru
Поступила в редакцию 07.04.2021
После доработки 02.08.2021
Принята к публикации 06.08.2021
Аннотация
Рассматриваются процедуры моделирования редких событий, к числу которых относится дефицит мощности и энергии при анализе балансовой надежности электроэнергетических систем статистическими методами. Показано, что основным направлением здесь является использование итерационных методов формирования последовательности вложенных вероятностных подпространств с их убывающей вероятностью. Рассмотрены реализации метода подпространств. Предложена модификация энтропийного метода, заключающаяся в гладкой адаптации индикаторной функции. Выполнено сравнение обсуждаемых процедур.
ВВЕДЕНИЕ
Основная задача анализа балансовой надежности (БН) электроэнергетической системы (ЭЭС) – оценить вероятностные показатели (вероятность, частота, математическое ожидание (МО) и др.) дефицита мощности (ДМ) в ЭЭС, наличие которого рассматривается как нарушение (отказ) нормального функционирования ЭЭС [1–3]. Аналогом упомянутых показателей балансовой надежности за рубежом являются: LOLP (Loss of load probability), LOLF (Loss of load frequency), EPNS (Expected power not supplied) [4]. Их сравнительная оценка, соответствие и формулы преобразования описаны в [5].
Случайное состояние системы, в основном, характеризуется вероятностным характером нагрузки $L = \left\{ {{{L}_{i}},~i = 1, \ldots ,n} \right\},$ располагаемой генерации $G = \left\{ {{{G}_{i}},~i = 1, \ldots ,n} \right\}$ и топологии электрической сети. При этом дефициты мощности могут иметь как локальный (в отдельных подсистемах), так и глобальный (по ЭЭС в целом) характер. Локальные ДМ определяются, в основном, состоянием (включен – отключен) и пропускной способностью элементов электрической сети.
В зависимости от степени детализации и целевой направленности решаемой задачи ЭЭС могут рассматриваться как: концентрированные; с ограниченной пропускной способностью (ПС) межсистемных связей (МСС); и в полной конфигурации, с учетом систем управления [6]. Упомянутые структурные уровни характеризуются специфическими математическими моделями, определяемыми степенью детализации систем, совокупностью ограничений и допущений.
Структура 1 ориентирована, в основном, на определение оптимального резерва генерирующей мощности в задачах перспективного развития ЭЭС. Затраты на генерацию, как правило, существенно выше затрат на транспорт электроэнергии, поэтому задача развития ЭЭС часто решается поэтапно: развитие генерирующей подсистемы при условии достаточной пропускной способности электрической сети (концентрированная ЭЭС) и развитие электрической сети при условии заданной структуры генерирующей подсистемы.
На втором этапе ЭЭС рассматривается как система с ограниченной ПС МСС (структура 2). Здесь МСС с ограниченной ПС объединяют некоторое множество концентрированных ЭЭС, которые в России принято определять как зоны надежности [7] или зоны свободного перетока мощности [8]. Основной направленностью задач БН здесь является анализ возможности появления локальных дефицитов мощности, вызванных ограниченностью ПС МСС. Именно такая структура является объектом анализа в представленной работе.
Полная детализация ЭЭС с учетом систем управления режимами является предметом анализа режимной надежности; ориентирована на задачи развития систем автоматики и диспетчерского управления и в данной работе не рассматривается.
Следует отметить, что все технические системы, в том числе и ЭЭС, характеризуются малой (доли процента) вероятностью событий типа “отказ” (в БН ЭЭС – это дефицитное состояние ЭЭС). При этом, как правило, отказ проявляется при бесконечно большой комбинации внешних событий. Так в ЭЭС с двумя узлами нагрузки и фиксированной предельной мощностью электрических станций дефицит мощности может проявляться при недопустимо большом повышении нагрузки либо первого, либо второго, либо того и другого узлов. При этом величина превышения суммарной нагрузки над генерацией является непрерывной и отсюда бесконечно неопределенной в реализации величиной. Число узлов нагрузки и генерации реальных расчетных схем ЭЭС измеряется тысячами. Отсюда многократно возрастает неопределенность дефицитного состояния ЭЭС, становится затруднительным процесс идентификации наиболее значимых комбинаций событий, приводящих к отказу системы.
Основным математическим аппаратом при анализе надежности ЭЭС в настоящее время являются методы статистических испытаний и, в частности, метод Монте-Карло (ММК) [9–13 и др.]. Данные методы позволяют моделировать системы со сложными функциональными взаимосвязями, не поддающимися аналитическому описанию, в том числе учитывать стохастическую неопределенность, связанную с предложением, спросом и пропускной способностью межсистемных связей.
Известен основной недостаток ММК – для обеспечения точности результатов требуется достаточно большое число $N$ испытаний, поскольку $N$ обратно пропорционально вероятности моделируемых событий. В частности, при моделировании события с вероятностью 10–3 и погрешностью моделирования 1% требуется не менее 105 статистических испытаний [14]. При анализе балансовой надежности реальных ЭЭС наиболее значимыми являются кратные отказы (одновременный отказ двух линий электропередачи (ЛЭП), одновременный отказ ЛЭП и энергоблока, отказ энергоблока в период пиковых нагрузок и др.), поскольку единичные отказы электрооборудования ЭЭС как правило не приводят к ограничению электропотребления – ЭЭС проектируются и сооружаются с учетом критерия N-1, при котором единичный отказ любого элемента ЭЭС не должен приводить к отказу процесса электроснабжения потребителей. Вероятность кратных независимых отказов равна произведению вероятностей отказа отказавших элементов. В результате вероятность кратных отказов принимает значения 10–6–10–8. При этом для идентификации, моделирования и анализа послеаварийных состояний ЭЭС методом ММК требуется число испытаний не менее 107–109. При меньшем числе испытаний идентификация таких редких событий становится маловероятной, что приводит к значимой погрешности результирующих показателей БН. С учетом того, что при каждом испытании требуется выполнение оптимизационных расчетов (оптимальное потокораспределение) анализ БН ЭЭС потребует несколько часов машинного времени. Следует отметить, что расчет показателей надежности, как правило, является составной частью более общих задач, например, выбор оптимальной конфигурации электрической сети при ее развитии. Отсюда длительность расчета надежности варианта развития ЭЭС как отдельного расчетного блока лимитируется по времени. Современная энергосистема требует все более сложной детализации и расширения учитываемых факторов, что нелинейно увеличивает сложность задачи оценки надежности ЭЭС. В совокупности это приводит к нецелесообразности, а иногда и невозможности использования стандартного ММК для оценки БН энергосистемы. Требуются модификации ММК, направленные на увеличение вычислительной эффективности статистических методов.
Одним из путей решения проблемы выполнения большого числа относительно однотипных расчетов, связанных с моделированием в многомерном вероятностном пространстве редких (с вероятностью отказов менее 10–5) событий является идея параллельных вычислений. Технология одновременного использования нескольких компьютеров (или процессоров) активно развивается в течение последних 30 лет [15–17]. Параллельные вычисления, безусловно, снижают вычислительную нагрузку ММК. Однако зависимость между количеством параллельных вычислительных ресурсов и временем вычислений близка к линейной функции [17]. Отсюда положительный эффект распараллеливания вычислений становится не столь очевидным при моделировании редких событий.
Другим направлением является использование методов паттернов, метамоделей, искусственного иммунитета, искусственной нейронной сети, опорных векторов наименьших квадратов [18–21] и др. Эти методы также показали снижение вычислительной нагрузки метода ММК. Однако, как правило, для задач БН ЭЭС они не апробированы, ориентированы на определенный класс задач, зачастую малоэффективны и не обеспечивают требуемую точность и надежность идентификации событий с вероятностью менее 10–4, что характерно для реальных систем энергетики. Отсюда проблема идентификации редких событий остается по-прежнему актуальной.
Более универсальный характер имеют итерационные методы, связанные с преобразованием анализируемых пространств, функций вероятностных распределений случайных переменных и критериальных функций. Наиболее распространенными в данном классе методов являются методы подпространств и значимой выборки [22–25], а также кросс-энтропийные методы [26–28].
В данной работе предлагаются и анализируются новые процедуры определения вероятностных параметров редких событий, основанные на методах вложенных множеств: моно и полицентры формирования промежуточной выборки значимых событий, а также модификация кросс-энтропийного метода, основанная на мягком преобразовании функции распределения мощности нагрузки.
ДЕФИЦИТ МОЩНОСТИ КАК РЕДКОЕ СОБЫТИЕ
Пусть $x \in {{\mathbb{R}}^{m}}$ – случайный вектор, который объединяет все вероятностные входные переменные ${{L}_{i}},{{G}_{i}},$ и др. В простейшем случае, когда учитываются только располагаемая генерация и нагрузка и не учитываются случайные состояния элементов системы, температуры окружающей среды и др., $x = \left\{ {{{L}_{i}},{{G}_{i}},~~i = 1, \ldots ,n} \right\},$ где $i~$ – номер узла электрической сети. С целью концентрации внимания на механизмах идентификации редких событий, связанных с отказами функционирования ЭЭС множество случайных, вероятностно определенных величин в данной работе ограничено только нагрузкой и располагаемой генерацией.
Дефицитность системы определяется разностью $~{{D}_{{{\Sigma }}}} = ~{{L}_{{{\Sigma }}}} - {{G}_{{{\Sigma }}}}$ = $\sum {{{L}_{i}}} - \sum {{{G}_{i}}} ,\,\,{{L}_{{{\Sigma }}}} > {{G}_{{{\Sigma }}}}.$ Ее можно оценить, например, с$~$ помощью функции избыточности системы, $S = {{G}_{{{\Sigma }}}} - {{L}_{{{\Sigma }}}}$ или (при учете пропускной способности электрической сети) $S = \min \left( {{{G}_{i}} - {{L}_{i}},~\forall i} \right).$ При независимости $\left\{ {{{L}_{i}},{{G}_{i}}} \right\}$ часто имеет смысл рассматривать обобщенную случайную величину – располагаемая генерирующая мощность узла, ${{r}_{i}} = {{G}_{i}} - {{L}_{i}}$. Ее МО и дисперсия: ${{\mu }_{{{{r}_{i}}}}} = {{\mu }_{{{{G}_{i}}}}} - {{\mu }_{{{{L}_{i}}}}};$ $\sigma _{{{{r}_{i}}}}^{2} = \sigma _{{{{G}_{i}}}}^{2} + \sigma _{{{{L}_{i}}}}^{2}.$ В результате число управляющих стохастических переменных сокращается до числа узлов электрической сети. При этом ${{D}_{{{\Sigma }}}} = - {{r}_{{{\Sigma }}}} = - \sum {{{r}_{i}}} ,\,\,\,\,{{r}_{{{\Sigma }}}} < 0.$
В общем случае при анализе локальных ДМ необходимо учитывать законы распределения мощности в электрической сети. Каждый узел характеризуется экспортом ${{u}_{i}},~i = 1, \ldots ,n$ или импортом (–${{u}_{i}}$) мощности, определяемыми диспетчерским управлением ЭЭС и зависящими от располагаемой мощности узлов ${{u}_{i}} = {{u}_{i}}\left( r \right).$ При этом локальный ДМ ${{D}_{i}} = {{u}_{i}} - {{r}_{i}} = {{u}_{i}} - {{G}_{i}} + {{L}_{i}};$ ${{D}_{i}} > 0.$ При локальных ДМ системный ДМ фиксируется, если хотя бы в одном из узлов имеет место локальный ДМ $~{{D}_{{{\Sigma }}}} = \sum {{{D}_{i}}} .$ Для более точного учета дефицитности ЭЭС необходимо учитывать потери активной мощности в сети, которые определяются распределением потоков мощности $z = \left\{ {{{z}_{j}},j = 1, \ldots ,m} \right\}$ в элементах электрической сети и имеют нелинейный (квадратичный) характер. Учет потерь мощности связан с появлением дополнительного условия ${{\pi }_{{{\Sigma }}}} = \sum {{{u}_{i}}} .$ При этом ${{D}_{{{\Sigma }}}} = ~{{L}_{{{\Sigma }}}} - {{G}_{{{\Sigma }}}} + ~{{\pi }_{{{\Sigma }}}},$ ${{D}_{{{\Sigma }}}} \geqslant 0.$
Вектор $z$ определяется решением задачи оптимального распределения мощности нагрузки между источниками питания. В простейшем случае, приемлемом в задачах оценки надежности, можно считать $z = Cu{\text{,}}$ где $C$ – матрица потокораспределения [7]. В результате ДМ в ЭЭС представляет сложную (часто определяемую алгоритмически) функциональную зависимость от совокупности управляющих переменных, имеющих случайный характер.
Состояние дефицитности системы фиксируется, если некоторая заданная на множестве управляющих переменных критериальная функция $\psi (x)$ становится меньше заданного предельного значения ${{\psi }_{{{\text{lim}}}}}{\text{:}}$ $\psi \left( x \right) < {{\psi }_{{{\text{lim}}}}}.$ В практике для идентификации дефицитности чаще используется функция с нулевым порогом, $S\left( x \right) = \psi \left( x \right) - {{\psi }_{{{\text{lim}}}}},$ которая при дефицитности системы принимает, например, отрицательное значение, $S\left( x \right) < 0.$ При этом область
определяет совокупность дефицитных состояний системы.При учете локальных ДМ в ЭЭС критериальная функция имеет вид:
Критериальной функции соответствует индикаторная функция$:$
При заданной ПР $f\left( x \right)$ вероятность появления редкого события определяется областью H, удовлетворяющую критерию $S\left( x \right) < 0.$
Функцию $F\left( x \right)$ (или плотность$~f\left( x \right)$) распределения случайного вектора $x$ состояний системы практически невозможно представить в виде аналитического выражения, поскольку она является результатом свертки разнотипных, с различающимися параметрами большого числа параметров системы (нагрузки, генерации, бинарные переменные, определяющие состояние элементов системы, солнечная радиация, скорость ветра и др.). Именно поэтому основным методом анализа надежности ЭЭС в настоящее время является метод статистических испытаний, позволяющий путем многократных испытаний и их статистической обработки получить достаточно точную оценку искомых величин. При этом в качестве исходных данных, как правило, задаются параметры маржинальных распределений исходных случайных величин (например, нагрузка узла $i$ ЭЭС описывается нормальным (Гауссовским) распределением с математическим ожиданием ${{\mu }_{i}}$ и среднеквадратическим отклонением (СКО) ${{\sigma }_{i}},$ ${{L}_{i}}\sim N(x,{{\mu }_{i}},~{{\sigma }_{i}}).$
МЕТОД ПОДПРОСТРАНСТВ СОСТОЯНИЙ
Эффективность метода Монте-Карло может быть повышена за счет применения методов уменьшения дисперсии, таких как выборка по значимости. Основная идея данной группы методов – формирование последовательности подмножеств ${{H}_{1}} \supset {{H}_{2}} \supset \ldots \supset {{H}_{m}} = H$ пространства состояний системы, где каждое последующее подпространство увеличивает вероятность идентификации редких событий и определяется на базе предыдущего, образуя последовательность цепи Маркова. При этом вероятность появления редкого события
Каждое последующее подмножество выбирается так, чтобы вероятность условного события $\Pr \left( {{{H}_{j}}{\text{|}}{{H}_{{j - 1}}}} \right)$ была бы достаточно велика. В результате малая вероятность представляется произведением относительно больших вероятностей [23–25].
Одним из путей формирования $\left( {{{H}_{j}}{\text{|}}{{H}_{{j - 1}}}} \right)$ является отбор заданной доли ${{p}_{0}}$ наиболее значимых событий $X_{b}^{j} = \left( {x_{1}^{j},~x_{2}^{j}, \ldots ,x_{k}^{j}} \right),$ где $k = {{p}_{0}}N;$ $N$ – объем выборки. Индекс b характеризует максимальный для множества $X_{b}^{{j - 1}}$ уровень критериальной функции $\psi \left( x \right).$ Его более детальное определение дано ниже). Значимость событий определяется по величине $\psi \left( x \right)$ – чем меньше $\psi \left( x \right),$ тем больше значимость $x$ (при $\psi \left( {{{x}_{i}},i = 1,...k} \right) < 0$ вся область $X_{b}^{j}$ состоит из значимых событий типа “отказ” (дефицитные состояния ЭЭС)). Дифференциация по значимости определяет механизм формирования множества $X_{b}^{j}.$ Полная, полученная на основе данных этапа $j - 1$ выборка ${{H}_{{j - 1}}}$ упорядочивается по возрастанию $\psi \left( x \right){\text{:}}$ $\psi \left( {{{x}_{1}}} \right) \leqslant \ldots \leqslant \psi \left( {{{x}_{N}}} \right).$ Первые ${{p}_{0}}N~$ событий (${{p}_{0}} \times 100$ перцентиль функции $\psi \left( x \right)$) определяют множество $X_{b}^{j}$ и соответствующую ему максимальную величину критериальной функции, ${{b}_{j}} = {\text{max}}\left( {\psi \left( x \right),~x \in X_{b}^{j}} \right),$ которая, в свою очередь, является основой для формирования нового множества ${{H}_{j}} = \left\{ {~x{\kern 1pt} :\,\,~\psi \left( x \right) < {{b}_{j}}} \right\}.$ При этом величину ${{p}_{0}}$ можно рассматривать как вероятность условного события $\Pr \left( {{{H}_{j}}{\text{|}}{{H}_{{j - 1}}}} \right) = {{p}_{0}}.$
Представленный поэтапный процесс формирования множества редких событий характеризуется положительной величиной ${{b}_{j}} > 0$ на всех промежуточных этапах. Это означает, что множество $X_{b}^{j}$ содержит как события-отказы, $\psi \left( x \right) < 0,$ так и не являющиеся отказами $~\psi \left( x \right) > 0,$ т.е. принцип отбора событий сводится к исключению менее значимых событий и расширению области более значимых событий, ${{b}_{j}} < {{b}_{{j - 1}}}.$ Изначально ${{b}_{0}} = \infty ,$ что означает, принадлежность зоне анализа всех сгенерированных на базе маржинальных ПР состояний системы. Однако на последующих этапах при генерации анализируемого множества псевдослучайных состояний системы вводится ограничение: $\psi \left( x \right) < {{b}_{{j - 1}}}.$ Как правило, это реализуется заменой параметров ПР случайных переменных некоторыми новыми расчетными величинами.
На последнем этапе ${{b}_{j}} < 0.$ Это означает, что все события в выделяемой по принципу усечения множества с долей ${{p}_{0}}$ являются отказами. Но отказами могут быть и события, не попавшие в определяемую перцентилем область, ${{b}_{j}} < \psi \left( x \right) < 0.$ Здесь условная вероятность определяется согласно соотношению: $\Pr \left( {{{H}_{m}}{\text{|}}{{H}_{{m - 1}}}} \right) = {{N\left( {\psi \left( x \right) < 0} \right)} \mathord{\left/ {\vphantom {{N\left( {\psi \left( x \right) < 0} \right)} N}} \right. \kern-0em} N},$ где $N\left( {\psi \left( x \right) < 0} \right)~$ – число элементов выборки объема N, удовлетворяющих требованию $\psi \left( x \right) < 0.$
В зависимости от алгоритма полный объем выборки ${{N}^{{(j)}}}$ на промежуточных этапах может отличаться от заданного N, однако при этом сохраняется принцип отбора – к дальнейшему рассмотрению принимается только ${{p}_{0}}$ – часть сформированного для анализа множества состояний системы.
1.1. Моноцентр формирования промежуточной выборки
Относительно небольшая совокупность $X_{b}^{{j - 1}}$ является лишь базой для формирования ${{H}_{j}}.$ Ее элементы определяются согласно типу и параметрам функции распределения генерации псевдослучайных чисел на этапе $j - 1.$ На этапе $j~$ это должны быть иные параметры, с большей степенью идентификации редкого события. Одним из возможных вариантов формирования новой выборки предлагается генерация псевдослучайных чисел, распределенных по нормальному распределению с МО ${{\mu }^{j}} = \mathbb{E}\left( {x_{1}^{{j - 1}},~x_{2}^{{j - 1}}, \ldots ,x_{k}^{{j - 1}}} \right)$ и дисперсией ${{D}^{j}} = \mathbb{D}\left( {x_{1}^{{j - 1}},~x_{2}^{{j - 1}}, \ldots ,x_{k}^{{j - 1}}} \right).$ На первом этапе в качестве ${{\mu }^{{\left( 1 \right)}}},{{D}^{{\left( 1 \right)}}}$ принимаются МО и дисперсии рассматриваемой совокупности исходных случайных величин. Поскольку вектор с параметрами $\left( {{{\mu }^{j}},{{D}^{j}}} \right)$ является наилучшим представителем области ${{X}^{j}},$ то именно этот вектор целесообразно рассматривать в качестве центра области ${{H}_{j}}.$
Новое, сгенерированное на этапе $j$ множество псевдослучайных векторов с центром $\left( {{{\mu }^{j}},{{D}^{j}}} \right),$ в общем случае содержит точки, не принадлежащее ${{H}_{j}}$ по критерию ${{H}_{j}} \subset {{H}_{{j - 1}}},$ т.е. не удовлетворяющие условию $\psi \left( x \right) < {{b}_{{j - 1}}}.$ Решением данной проблемы является либо дополнение полученного множества до $N$ элементов, удовлетворяющих условию $\psi \left( x \right) < {{b}_{{j - 1}}},$ либо выполняется простое удаление неудовлетворительных состояний системы. В последнем случае выборка сокращается c $N$ до ${{N}_{j}}$ элементов, но все элементы оставшегося множества при этом принадлежат ${{H}_{j}}.$ Следует заметить, что число удаляемых элементов, как правило, относительно невелико и сокращение анализируемого множества слабо влияет на статистические оценки искомых параметров (в частности, на вероятность и МО дефицита мощности).
Расчеты показывают, что выбор $\left( {{{\mu }^{j}},{{D}^{j}}} \right)$ в качестве центра формирования множества ${{F}_{j}}$ приводит к некоторому завышению вероятности редкого события в области очень малых вероятностей (порядок: 10–6 по отношению к 10–7). Более точным является выбор центра в точке ${{x}^{{*j}}},$ соответствующей максимальному на этапе $j - 1$ значению критериальной функции, $\psi \left( {{{x}^{{*j}}}} \right)$ = ${{b}_{{j - 1}}}.$ Здесь априори допускается, что не менее половины новой генерации состояний системы не будут удовлетворять условию $\psi \left( x \right)$ < ${{b}_{j}},$ однако при этом увеличивается вероятность учета тех состояний, которые не попадают в статистическую выборку с центром $\left( {{{\mu }^{j}},{{D}^{j}}} \right).$ Увеличение доли удаляемых событий неразрывно связано с требованием увеличением объема выборки N. Сдвиг центра $\left( {{{\mu }^{{*j}}} = {{x}^{{*j - 1}}},{{D}^{{*j}}}} \right)$ выборки относительно МО приводит к необходимости коррекции дисперсии ${{D}^{{*j}}} = {{D}^{j}} + {{\left| {{{x}^{{*j - 1}}} - {{\mu }^{j}}} \right|}^{2}}.$
1.2. Метод опорных точек
Моноцентричный подход предполагает концентрацию выборки вокруг некоторого центра, например, согласно нормальному (Гауссовскому) распределению с МО в центре выборки. Однако принцип выделения периферийной области по вероятности ${{p}_{0}}$ и несимметрия области редкого события (чем больше нагрузка, тем больше дефицит мощности) заставляет усомниться в правомочности Гауссовского распределения на промежуточных этапах. Логически более оправданным здесь является вероятностное распределение, неизвестное по типу, но представленное определенной на предшествующем этапе совокупностью (опорных) точек ${{C}_{{j - 1}}} = \left( {x_{1}^{{j - 1}},~x_{2}^{{j - 1}}, \ldots ,x_{k}^{{j - 1}}} \right).$ Статистическое моделирование данного распределения возможно путем представления множества ${{H}_{j}}$ в виде объединения подмножеств с центрами в опорных точках ${{H}_{j}} = \bigcup {{{H}_{{js}}}\left( {x_{s}^{{j - 1}}} \right)} .$ В качестве СКО ${{\sigma }_{j}}$ при формировании множества ${{H}_{{js}}}$ можно рассматривать максимальное расстояние между точками множества ${{C}_{{j - 1}}}{\text{:}}$ ${{\sigma }_{j}} = \max \left| {x_{k}^{{j - 1}} - x_{l}^{{j - 1}}} \right|,$ $\left( {~x_{k}^{{j - 1}},x_{l}^{{j - 1}}} \right) \in {{C}_{{j - 1}}}.$ Это позволяет обеспечить пересечение множеств точек, формируемых в многомерных сферах с центрами в точках $x_{k}^{{j - 1}} \in {{C}_{{j - 1}}},$ а следовательно более полно и равномерно учесть область ${{C}_{{j - 1}}}.$
Основная проблема методов вложенных подпространств состояний является зависимость результирующих данных от механизма формирования промежуточных множеств. При этом возможны ситуации, когда последующее подпространство практически не меняет критериальный порог ${{b}_{k}} \approx {{b}_{{k - 1}}},$ что приводит к отсутствию сходимости вычислительного процесса за заданное число итераций. При этом результирующая вероятность редкого события становится сколь угодно малой. Отсюда основные направления исследований в этой области направлены на повышение робастности методов. Существует достаточно большое число предложений по формированию промежуточных множеств [22–25]. Наряду с описанными выше моноцентричными методами нами предложен и апробирован метод адаптивной выборки, сущность которого заключается в многократной адаптивной коррекции параметров (сдвиг и дисперсия) распределения промежуточной выборки.
АЛГОРИТМ АДАПТИВНОЙ ВЫБОРКИ
1. Инициализация: $k = 1;$ ${{N}_{c}} = {{p}_{0}}N;$ ${{N}_{s}} = {1 \mathord{\left/ {\vphantom {1 {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}};$ $\lambda = 0.6.$
2. Генерация по стандартному нормальному (Гауссовскому) распределению $N$ псевдослучайных чисел: $U = \left\{ {{{u}_{1}}, \ldots ,{{u}_{N}}} \right\}.$
3. Преобразование множества $U$ в матрицу $X = \left\{ {{{x}_{1}}, \ldots ,{{x}_{N}}} \right\}$ именованных случайных переменных (нагрузка, генерация, состояние элементов системы), согласно их маржинальным законам распределения ${{x}_{i}} = {{{{\varphi }}}_{i}}\left( {{{u}_{i}}} \right).$
4. Определение вектора критериальных функций $\psi = \left\{ {{{\psi }_{i}}\left( {{{x}_{i}}} \right)} \right\}$ и его сортировка по возрастанию функции: ${{\psi }_{i}}\left( {{{x}_{i}}} \right) \geqslant {{\psi }_{{i - 1}}}\left( {{{x}_{{i - 1}}}} \right).$
5. Определение на множестве $\psi $ перцентиля $\left( {{{p}_{0}} \times 100} \right),$ соответствующему ему параметра ${{b}_{k}} \geqslant 0$ и множества именованных значимых состояний системы ${{H}_{{xk}}} = \left\{ {{{x}_{i}}:{{\psi }_{i}}\left( {{{x}_{i}}} \right) < {{b}_{k}}} \right\}.$
6. Генерация новой выборки N случайных состояний системы на базе полученных в п. 5 опорных состояний системы согласно алгоритму адаптивной выборки, где после определенного числа генераций меняются МО и СКО нормального распределения, согласно которому осуществляется генерация случайных чисел.
7. Пп. 4–6 повторяются до тех пор, пока ${{b}_{k}} \geqslant 0.$ При этом условная вероятность ${\text{Pr}}\left( {{{H}_{k}}\left| {{{H}_{{k - 1}}}} \right.} \right) = {{p}_{0}}.$ На последнем шаге m, при ${{b}_{m}} < 0,$ определяется число ${{N}_{m}}{\text{\;}}$элементов, удовлетворяющих условию ${{\psi }_{{{{N}_{m}}}}}\left( {{{x}_{{{{N}_{m}}}}}} \right) \leqslant 0,$ ${{\psi }_{{{{N}_{m}} + 1}}}\left( {{{x}_{{{{N}_{m}} + 1}}}} \right) > 0.$ Результирующая вероятность редкого события $\Pr \left( H \right) = {{p_{0}^{{m - 1}}{{N}_{m}}} \mathord{\left/ {\vphantom {{p_{0}^{{m - 1}}{{N}_{m}}} N}} \right. \kern-0em} N}.$
8. Определение остальных анализируемых вероятностных показателей (МО дефицита мощности и др.).
КРОСС-ЭНТРОПИЙНЫЙ МЕТОД
Кросс-энтропийный метод (КЭМ) [26–28] основан на замене реальной функции $f\left( x \right)$ плотности распределения анализируемой многомерной случайной величины, по которой делается выборка ММК, некоторой вспомогательной функцией плотности распределения (ВПР) $q\left( x \right),$ смещающей сферу анализа в область представляющего интерес редкого события. Данный подход широко известен при вычислении интегралов сложных функций статистическими методами, где подынтегральная функция умножается и делится на некоторую функцию ПР, полностью определенную на рассматриваемом интервале интегрирования:
При этом возникает проблема выбора вспомогательной функции – необходимо, чтобы основанная на ней расчетная процедура была бы не только адекватной по направленности (смещения анализируемой области в сторону редкого события), но и эффективной по быстродействию и сходимости. При наличии ВПР вероятность дефицита мощности (2), может быть представлена в виде математического ожидания (МО) взвешенной индикаторной функции $J\left( x \right)W\left( x \right),$ определенной в многомерном пространстве случайных величин с плотностью распределения $q\left( x \right){\text{:}}$
(3)
${{\mathbb{P}}_{H}} = \int {J\left( x \right)\frac{{f\left( x \right)}}{{q\left( x \right)}}q\left( x \right)dx} = \int {J\left( x \right)W\left( x \right)q\left( x \right)dx} = {{\mathbb{E}}_{q}}\left[ {J\left( x \right)W\left( x \right)} \right],$Нетрудно видеть, что в выражении (3) $q\left( x \right)$ может быть любой функцией, лишь бы она удовлетворяла требования, предъявляемым к ПР. При этом не обязательно, чтобы она принадлежала к тому же классу ПР, что и $f\left( x \right).$ Как правило, в качестве $q\left( x \right)$ принимается ПР многомерного нормального распределения.
При моделировании случайных состояний системы $\{ {{x}_{i}},i = 1,....,N\} $ методом Монте-Карло на базе плотности распределения $q\left( x \right)$ и набора дискретных состояний системы $\left\{ {{{x}_{i}}} \right\}$ вероятность (3) редкого события трансформируется к виду:
(4)
${{\hat {\mathbb{P}}}_{H}} = \frac{1}{N}\sum\limits_{i = 1}^N {J({{x}_{i}})W\left( {{{x}_{i}}} \right)} ,$Дисперсия $\mathbb{V}({{\hat {\mathbb{P}}}_{F}})$ оценки вероятности определяется как средняя дисперсий случайной величины, распределенной по закону Бернулли:
Коэффициент вариации $\mathbb{C}\mathbb{V}{\text{,}}$ как мера ошибки оценки измеряемой случайной величины (вероятности ${{\hat {\mathbb{P}}}_{H}}$), определяется отношением стандартного отклонения к МО. В частности, для квадрата $\mathbb{C}{{\mathbb{V}}^{2}}\left( {{{{\hat {\mathbb{P}}}}_{H}}} \right){\text{:}}$
Отсюда видно, что коэффициент вариации (КВ) при моделировании по методу Монте-Карло обратно пропорционален $\sqrt {N{{\mathbb{P}}_{F}}} $ и поэтому для получения достаточно точной оценки вероятности рассматриваемого события при малых ${{\mathbb{P}}_{F}}$ для обеспечения приемлемого $\mathbb{C}\mathbb{V} = 0.1 - 0.2$ необходимо чрезвычайно большое количество N испытаний ($\sim {{10}^{5}}$ при $\mathbb{C}\mathbb{V} = 0.1$ и ${{\mathbb{P}}_{F}} = 0.001$).
В качестве критерия оптимизации при выборе наиболее эффективной в классе $\left\{ {q\left( x \right)} \right\}$ функции $q{\text{*}}(x)$ может служить минимум дисперсии ${{\mathbb{P}}_{F}}{\text{:}}$
Теоретически наилучшей функцией, приводящей к нулевой дисперсии искомой оценки вероятности ${{\mathbb{P}}_{H}}$, является функция [28]:
(5)
$q{\text{*}}\left( x \right) = \frac{{J\left( x \right)f\left( x \right)}}{{\int {J\left( x \right)f\left( x \right)dx} }} = \frac{{J\left( x \right)f\left( x \right)}}{{{{\mathbb{P}}_{H}}}}.$Поскольку оптимальная ВПР зависит от неизвестных величин ${{\mathbb{P}}_{H}}{\text{\;}}$и $J\left( x \right)$ непосредственное аналитическое определение $q{\text{*}}\left( x \right)$ невозможно. Достаточно хорошее приближение позволяет получить КЭМ, основанный на последовательном уточнении параметров $v$ многомерной плотности распределения $q\left( {x,~v} \right),$ и процедура определения результирующей величины представляется в виде цепи Маркова с выбором параметров ВПР на каждом шаге. Для оценки параметров v данный метод использует результаты промежуточных статистических испытаний. Вектор параметров v определяется путем минимизации кросс-энтропии (KL-дивергенции) [28].
KL-дивергенция определяет меру близости двух произвольных ПР ${{p}_{1}}\left( x \right);$ ${{p}_{2}}\left( x \right){\text{:}}$
В данной работе в качестве ${{p}_{1}}\left( x \right);$ ${{p}_{2}}\left( x \right)$ принимаются соответственно оптимальная ПР $q{\text{*}}\left( x \right)~и~$ ее текущая оценка $q\left( {x;v} \right).$ KL-дивергенция ${{\mathbb{D}}_{{KL}}}\left( {q{\text{*}}(x),q\left( {x;v} \right)} \right)$ определяет близость между этими функциями. В предлагаемой работе функция $q\left( {x;v} \right)$ представляется плотностью многомерного нормального распределения с математическим ожиданием ${{\mu }_{q}}$ и матрицей корреляционных моментов ${{{{\Sigma }}}_{q}}.$ В такой постановке степень оптимальности, по существу, определяет вектор параметров $v = [{{\mu }_{q}};{{{{\Sigma }}}_{q}}]$). При этом процедура оптимизации может быть представлена в виде:
(6)
$\begin{gathered} {{v}^{*}} = \mathop {{\text{argmin}}}\limits_v ~{{\mathbb{D}}_{{KL}}}\left( {{{q}^{*}}\left( x \right),q(x;v)} \right) = \mathop {{\text{argmax\;}}}\limits_v {{\mathbb{E}}_{{q*}}}\left[ {\ln \left( {q\left( {x;v} \right)} \right)} \right] = \\ = \mathop {{\text{argmax\;}}}\limits_v \int {\ln (q\left( {x;v} \right))q{\text{*}}(x)dx} . \\ \end{gathered} $Подставляя для определения v* наилучшую ПР (5) в полученное выражение и рассматривая ${{\mathbb{P}}_{H}}$ как константу, получаем:
При использовании ВПР $q\left( x \right)$
(7)
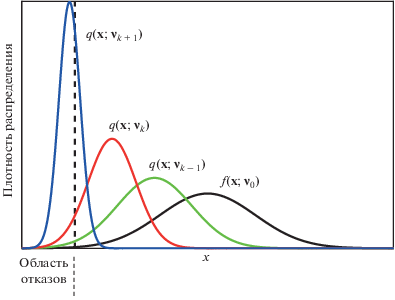
${{v}^{*}} = \mathop {{\text{argmax}}}\limits_v \left[ {\frac{1}{N}\sum\limits_{i = 1}^N {J\left( {{{x}_{i}}} \right)W\left( {{{x}_{i}}} \right)\ln (q\left( {{{x}_{i}};v)} \right)} } \right],$КЭМ решает проблему оптимизации итеративно путем определения ряда промежуточных плотностей распределения $\{ q(x;{{v}_{k}}),k = 1,....,NT\} ,$ которые, как показано на рис. 1, постепенно приближаются к целевой плотности $q{\text{*}}\left( x \right),$ представляющей область существования редкого события.
На шаге $k$ оптимальная ПР $q{\text{*}}\left( x \right)$ может быть представлена оценкой $q\left( {x;v_{{k - 1}}^{*}} \right)$ с полученными на предыдущем шаге оптимальными параметрами $v_{{k - 1}}^{*}.$ При этом $~W\left( {x;v_{{k - 1}}^{*}} \right) = {{f(x)} \mathord{\left/ {\vphantom {{f(x)} {q\left( {x;v_{{k - 1}}^{*}} \right)}}} \right. \kern-0em} {q\left( {x;v_{{k - 1}}^{*}} \right)}}.$ Область ${{H}_{k}}$ промежуточного множества состояний системы определяется порогом ${{b}_{k}}{\text{:}}$
(8)
${{H}_{k}} = \left\{ {x{\kern 1pt} :\,\,~{{\psi }_{k}}\left( x \right) < {{b}_{k}}} \right\},\,\,\,\,{{J}_{k}}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1,\,\,\,\,{{\psi }_{k}}\left( {{{x}_{k}}} \right) < {{b}_{k}};} \\ {0,\,\,\,\,{{\psi }_{k}}\left( {{{x}_{k}}} \right) \geqslant {{b}_{k}}.} \end{array}} \right.$Порог ${{b}_{k}}$ вычисляется как θ-квантиль (например, дециль полученных в процессе статистических испытаний и отсортированных от наименьшего к наибольшему значениям пороговой функции ${{\psi }_{i}}\left( {{{x}_{i}}} \right).$ При этом моделирование выполняется согласно плотности распределения $q(x;{{v}_{{k - 1}}})$ с параметрами ${{v}_{{k - 1}}}.$
Полученный в результате решения задачи оптимизации на шаге $k - 1$ вектор $v{\text{*}}$ рассматривается как новое значение вектора параметров оптимальной ПР $q{\text{*}}\left( x \right),$ ${{v}_{k}} = v{\text{*}}.$ Начиная от исходного вектора параметров ${{v}_{0}},$ каждый последующий вектор ${{v}_{k}}$ определяется решением оптимизационной задачи (7), (9), приближаясь к оптимальной плотности распределения $q{\text{*}}\left( x \right) = \mathop {\lim }\limits_{k \to \infty } \left( {q(x;{{v}_{k}}){\text{\;}}} \right),$ которая, в свою очередь, является наилучшей оценкой оптимальной в кросс-энтропийном методе вспомогательной ПР.
При этом $W\left( {{{x}_{i}};{{v}_{{k - 1}}}} \right) = {{f(x)} \mathord{\left/ {\vphantom {{f(x)} {q\left( {x;{{v}_{{k - 1}}}} \right)}}} \right. \kern-0em} {q\left( {x;{{v}_{{k - 1}}}} \right)}}.$
Процедура повторяется до тех пор, пока ${{b}_{k}}$ не станет отрицательной, или, по крайней мере, $\theta \in [0.01,~0.1]$ испытаний не разместятся в искомой области редких событий [28]. Если число шагов до достижения критерия окончания итерационного процесса составляет m, то результирующая вероятность редкого события:
(10)
${{\hat {\mathbb{P}}}_{F}} = \frac{1}{N}\sum\limits_{i = 1}^N {J\left( {{{x}_{i}}} \right)W\left( {{{x}_{i}};{{v}_{{m - 1}}}} \right)} .$Как было упомянуто, вектор ${{v}_{0}}$ принимается равным исходным параметрам вероятностных распределений анализируемых случайных величин, т.е. при заданном $N$ и нулевом пороговом значении определяемая соотношением (8) область ${{H}_{0}},$ может и не содержать ни единого редкого события, что приводит к вырожденности оптимизационной процедуры (9). Именно поэтому область ${{H}_{k}}$ расширяется за счет ненулевого порогового значения ${{b}_{k}}.$ В результате в число событий-отказов войдут “почти отказы”. Отсюда отказы становятся менее редкими и идентифицируются в выборке.
Алгоритм CEM:
1. Ввод исходных данных (${{v}_{0}}$ – параметры функций распределения случайных переменных). Инициализация переменных, $k = 0;$ $N$ – объем выборки Монте-Карло; $\theta $ – квантиль выборки;
2. На базе $q(x;{{v}_{{k - 1}}})$ генерация (метод Монте-Карло) матрицы Х псевдослучайных состояний системы, $\dim X = Nn,$ где $n$ – число случайных переменных системы $x = ({{x}_{i}},i = 1, \ldots ,N),$ ${{x}_{i}} = \left( {{{x}_{{ij}}},j = 1, \ldots ,n)} \right..$
3. Формирование векторов:
4. Определение (либо через квантиль отсортированного массива ψ, либо статистически, через ${{\mu }_{{{\psi }}}};{{\sigma }_{{{\psi }}}}$) порогового предела ${{b}_{k}}$ критериальной функции $\psi \left( x \right).$
5. Формирование области редкого события ${{H}_{k}} = \left\{ {x{\kern 1pt} :\psi \left( x \right) < {{b}_{k}}} \right\}.$
6. Оптимизация:
7. Пп. 2–6 повторяются до тех пор, пока ${{b}_{k}}{\text{\;}} > 0,$ при $k = k + 1.$
8. Формирование: $J\left( {x,{\text{\;}}0} \right),W\left( {x,{{v}_{k}}} \right),{{P}_{{{\text{откл}}}}}.$
9. Определение результирующих величин: вероятности ${\text{Pr}} = \frac{1}{N}\sum\nolimits_{i = 1}^N {J\left( {{{x}_{i}}} \right)W\left( {{{x}_{i}};{{v}_{{m - 1}}}} \right)} ;$ МО дефицита мощности ${{\mu }_{{\text{Д}}}} = - \frac{1}{N}\sum {\psi \left( {{{x}_{i}}} \right)J\left( {{{x}_{i}}} \right)W\left( {{{x}_{i}},{{v}_{{m - 1}}}} \right)} $ и др.
1.3. Упрощенный кросс-энтропийный метод
Представленный выше классический КЭМ требует выполнения оптимизационной процедуры при определении параметров ${{v}_{k}}$ текущей ПР $q\left( {x,~{{v}_{k}}} \right).$ При этом ${{v}_{k}}$ включает в себя МО ${{\mu }_{k}}$ и матрицу корреляционных моментов ${{\Sigma }_{k}}$ тех реализаций x, которые относятся к области ${{H}_{k}},$ $x \in {{H}_{k}}.$ Выражение (10) можно рассматривать как среднее значение величин ${{J}_{F}}\left( {{{x}_{i}}} \right)$ с весами $W\left( {{{x}_{i}}} \right).$ Поскольку оно относится к вероятности, то каждая составляющая суммы может интерпретироваться как вероятность того, что реализация ${{x}_{i}}$ принадлежит текущей области ${{H}_{k}}$ редкого события. Поскольку область ${{H}_{k}}$ определена индикаторной функцией ${{J}_{k}}\left( {{{x}_{i}}} \right),$ то МО располагаемой мощности узлов$~$в области ${{H}_{k}}$
Матрица корреляционных моментов
Данные параметры формируют вектор ${{v}_{k}}.$ При таком подходе не требуется оптимизационная процедура, что существенно сокращает длительность расчетов без существенного снижения точности результатов.
1.4. Модифицированный кросс-энтропийный метод
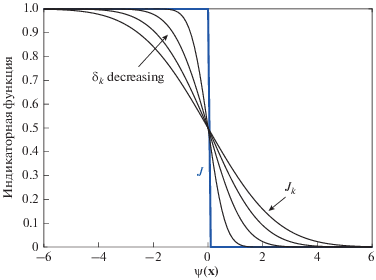
В традиционном КЭМ промежуточная область существования редкого события определяется дискретно через априори задаваемый квантиль, который формирует порог чувствительности ${{b}_{k}},$ что часто приводит к потере значимой информации (потере событий, связанных с дефицитом мощности). Это возможно из-за относительно небольшого (с целью ускорения расчетов) объема “тестовой” выборки на шаге k или достаточно грубого ограничения области ${{H}_{m}}$ на последнем шаге. Нами предлагается более “мягкая” процедура идентификации области редкого события. Если в традиционном КЭМ изменение индикаторной функции от 0 к 1 происходит дискретно в точке $b = 0$, что позволяет интерпретировать индикаторную функцию как функцию распределения вырожденной случайной величины, то в модифицированном кросс-энтропийном методе (МКЭМ) принимается, что индикаторная функция как функция вероятностного распределения с МО в точке 0 обладает некоторой дисперсией, итеративно приближающейся к нулю (рис. 2). В результате в МКЭМ определяемая индикаторной функцией ${{J}_{k}}(x)$ промежуточная область редкого события формируется функцией гладкого приближения. Это обеспечивает плавный переход от приблизительно оптимальной ПР $q_{k}^{*}(x)$ к оптимальной ПР с учетом практически всех дефицитных состояний ЭЭС.
Предельная индикаторная функция в МКЭМ представляется в виде:
При этом на промежуточных этапах величина ${{\delta }_{k}} > 0.$
При $\psi \left( x \right) > 0,$ ${{{{\delta }}}_{k}}{\text{\;}} \to 0$ индикаторная функция ${{J}_{k}}\left( {x;{{\delta }_{k}}} \right) \to 0{\text{\;,}}$ а при $\psi \left( x \right) < 0,$ $~{{{{\delta }}}_{k}}{\text{\;}} \to 0$ индикаторная функция ${{J}_{k}}\left( {x;{{\delta }_{k}}} \right) \to 1,$ т.е. вырождается в единичный скачек первого рода, что соответствует требованиям идеальной идентификации редкого события. Цепь ${{\delta }_{0}} > {{\delta }_{1}} > .... > {{\delta }_{m}} > 0$ определяет убывающую последовательность ширины зоны неопределенности решения (рис. 2). При учете нового представления индикаторной функции условие (9) трансформируется к виду:
(11)
${{v}_{k}} = \mathop {{\text{argmax}}}\limits_v \left[ {\frac{1}{N}\sum\limits_{i = 1}^N {\Phi \left( { - \frac{{\psi \left( {{{x}_{i}}} \right)}}{{{{\delta }_{k}}}}} \right)W\left( {{{x}_{i}};{{v}_{{k - 1}}}} \right)\ln (q\left( {{{x}_{i}};v} \right))} } \right].$Величина ${{\delta }_{k}}$ определяется (корректируется) исходя из условия наилучшей аппроксимации ПР $q_{k}^{*}\left( x \right)$ по выборке, полученной на базе $q(x;{{v}_{{k - 1}}}).$ Данному условию соответствует минимум дисперсии функции ${{\varphi }_{k}}({{x}_{i}};{{v}_{{k - 1}}},{{\delta }_{k}})$ = $\Phi \left( {{{ - \psi \left( {{{x}_{i}}} \right)} \mathord{\left/ {\vphantom {{ - \psi \left( {{{x}_{i}}} \right)} {{{\delta }_{k}}}}} \right. \kern-0em} {{{\delta }_{k}}}}} \right)W\left( {{{x}_{i}};{{v}_{{k - 1}}}} \right),$ $i = 1,...,N.$ Это достигается минимизацией разности между коэффициентами вариации $\mathbb{C}\mathbb{V}$ функции ${{\varphi }_{k}}(x;{{v}_{{k - 1}}},{{\delta }_{k}})$ и априори заданного для обеспечения требуемой точности результатов коэффициента вариации $\mathbb{C}{{\mathbb{V}}_{{target}}}$ (в тестовых расчетах $\mathbb{C}{{\mathbb{V}}_{{target}}} = 1.5$):
Данный критерий является отражением следующих математических построений. В теории статистики рассматриваются взвешенные случайные величины (например, при определении МО взвешенной индикаторной функции (11)). При этом допускается (и в нашем случае это имеет место), что весовые коэффициенты могут изменяться в процессе итерационного процесса. Критерием, который позволяет максимально полно учесть вариацию весов, является эффективный размер выборки (ESS) (число проб с ненулевым весом), который приближенно оценивает необходимое количество статистических выборок. ESS часто используется в адаптивных последовательных реализациях Монте-Карло типа байесовских решений и может быть выражена через $\mathbb{C}\mathbb{V}$ весов [28, 29] как:
Подбор эффективного размера выборки эквивалентен подбору коэффициента вариации весов $\mathbb{C}{{\mathbb{V}}_{{{{W}_{k}}}}},$ как показано в этих уравнениях:
Начиная с ${{\delta }_{0}} = \infty $ и ${{v}_{0}},$ процедура повторяется итерационно и прекращается, когда коэффициенты вариации, $\mathbb{C}\mathbb{V}$ весов текущей мягкой аппроксимации ПР $q{\text{*}}(x)$ ниже, чем $\mathbb{C}{{\mathbb{V}}_{{target}}}.$ При этом
Необходимое число итераций $m$ здесь зависит от соотношения коэффициентов вариации и в качестве результирующей принимается ПР $q_{k}^{*}\left( x \right),$ полученная на последней итерации. Расчеты показывают, что использование $\mathbb{C}\mathbb{V}$ весов в качестве критерия остановки вместо параметрической плотности $q(x;{{{v}}_{{k - 1}}})$ улучшает надежность (robustness) сходимости метода.
Возникает вопрос: почему $\mathbb{C}{{\mathbb{V}}_{{target}}} = 1.5?$ Действительно, в практических расчетах приемлемым считается КВ, не превышающий 0.2–0.3. Здесь следует принять во внимание, что квадрат КВ выборки равен среднему квадратов КВ реализаций поскольку МО среднего по выборке равно МО рассматриваемой случайной величины, $\mathbb{E}\left( {\bar {x} = {{\left( {\sum {{{x}_{i}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum {{{x}_{i}}} } \right)} N}} \right. \kern-0em} N}} \right) = {{\mu }_{x}},$ а дисперсия случайной величины $\bar {x}$ $\mathbb{D}\left( {\bar {x}} \right) = {{{{D}_{x}}} \mathord{\left/ {\vphantom {{{{D}_{x}}} N}} \right. \kern-0em} N}.$ Отсюда
Применительно к функции ${{\hat {\varphi }}_{k}}$ и вероятности ${{\hat {\mathbb{P}}}_{H}}{\text{:}}$
Если $\mathbb{C}{{\mathbb{V}}_{{{{{{\varphi }}}_{k}}}}} = 1.5,$ то при $N = 1000$ имеем${\text{\;}}\mathbb{C}\mathbb{V}\left( {{{{\hat {\mathbb{P}}}}_{H}}} \right)$ = 0.047, что вполне удовлетворяет требованиям практики.
Алгоритм $ECEM$
1. Ввод исходных данных: ${{v}_{0}},$ $\mathbb{C}{{\mathbb{V}}_{{target}}}.$ Начальные присвоения $k{\text{\;}} = {\text{\;}}0,$ ${{\delta }_{k}}$ = ∞.
2. k = k + 1. Генерация N реализаций состояний системы x на базе Гауссовского распределения с плотностью $q\left( {x,{{v}_{{k - 1}}}} \right).$
3. Формирование векторов: $J\left( {x,{{\delta }_{{k - 1}}}} \right);$ $q\left( {x,{{v}_{{k - 1}}}} \right);$ $\psi \left( x \right),$ а также
4. Определение ${{\delta }_{k}}$ при оптимизации: ${{\delta }_{k}} = \mathop {{\text{argmin}}}\limits_{{{{{\delta }}}_{k}} \in (0,{{{{\delta }}}_{{k - 1}}})} \left| {\mathbb{C}{{\mathbb{V}}_{{{{W}_{k}}}}} - \mathbb{C}{{\mathbb{V}}_{{target}}}} \right|.$
5. Определение ${{{v}}_{k}}$ при оптимизации: ${{{v}}_{k}} = \mathop {{\text{argmax}}}\limits_{{{{v}}_{k}}} \left[ {\frac{1}{N}\sum\nolimits_{i = 1}^N {{{W}_{k}}\left( {{{x}_{i}};{{{v}}_{{k - 1}}}} \right)\ln (q\left( {{{x}_{i}};{{{v}}_{k}}} \right))} } \right].$
6. Пп. 2–5 выполняются до тех пор, пока коэффициенты вариации ℂ𝕍 весов больше заданных $\mathbb{C}{{\mathbb{V}}_{{target}}}.$
7. Расчет всех требуемых показателей надежности на базе полученных параметров области редких событий.
ПРОВЕРОЧНЫЕ РАСЧЕТЫ
Для сравнения описанных процедур были выполнены расчеты показателей балансовой надежности пяти-узловой электрической схемы. Результаты расчетов представлены в табл. 1, где обозначены методы: ММК – классический метод Монте-Карло (при 107 испытаниях); Моноцентр – метод подпространств с одной точкой формирования промежуточного подпространства; Полицентр – в качестве опорных точек формирования промежуточного подпространства ${{H}_{k}}$ принимается множество ${{H}_{{k - 1}}};$ SubSet – метод вложенных пространств с изменяющимися параметрами вероятностных распределений при формировании промежуточного подпространства; СЕ – классический кросс-энтропийный метод; ECE – модифицированный кросс-энтропийный метод.
Таблица 1.
Проверочные расчеты
| Метод | Pr, 10–5 | Pr, Сv | Pr_Eps, % | mD, 10–4 | mD, Сv | mD_Eps, % | t, сек |
|---|---|---|---|---|---|---|---|
| Точное значение | 2.23 | 0 | 0 | 1.21 | 0 | 0 | 0 |
| ММК | 2.23 | 0.07 | 0.1% | 1.21 | 0.10 | 0.1% | 19.02 |
| Mоноцентр | 2.24 | 0.6 | 0.5% | 1.48 | 0.90 | 22.1% | 0.44 |
| Полицентр | 2.29 | 0.65 | 2.9% | 1.52 | 0.92 | 25.7% | 0.19 |
| SubSet (ад.выб) | 2.2 | 0.58 | –1.4% | 1.41 | 0.92 | 16.7% | 3.21 |
| CE | 2.3 | 0.54 | 3.3% | 1.24 | 0.03 | 2.5% | 0.12 |
| ECE | 2.29 | 0.55 | 2.7% | 1.14 | 0.03 | –5.6% | 0.95 |
Во втором столбце представлена вычисленная вероятность суммарного дефицита мощности ЭЭС. Следует отметить, что все представленные методы показывают приемлемую для практических расчетов точность редкого события – максимальное отклонение 3.3% (столбец Pr_Eps, %, метод СЕ) при точном значении вероятности Pr = = 2.23 × 10–5 можно считать незначительным для малых вероятностей. Для сравнения можно упомянуть, что при таких вероятностях широко распространенная замена биномиального распределения распределением Пуассона имеет гораздо большую погрешность [29].
Последующие 3 столбца относятся к МО дефицита мощности. Здесь разброс (коэффициент вариации, столбец mD, Сv) результирующих величин значительно больше. Следует отметить, что относительная ошибка расчета МО дефицита мощности (коэффициент вариации, столбец mD, Сv)) превышает 25%. Увеличение точности возможно за счет увеличения объема промежуточной выборки. Однако это приводит к увеличению длительности расчетов (столбец t), которая в представленных расчетных процедурах зависит в основном от емких по времени преобразований вероятностных распределений (равномерное – Гауссовское – индивидуальное (маржинальное)). Если принять, что все случайные величины описываются одним и тем же нормальным распределением (с отличающимися параметрами), то это позволяет снизить длительность расчетов в несколько раз.
Полученные результаты позволяют рекомендовать для практического применения обеспечивающие наименьший разброс результирующих показателей кросс-энтропийные методы.
ЗАКЛЮЧЕНИЕ
Описанные методы идентификации редких в электроэнергетике событий относятся к тем событиям, для которых можно определить критериальную функцию, меняющую свою величину в зависимости от удаленности от искомых событий. К таким функциям (и событиям) в электроэнергетике можно отнести дефицит мощности, положительный при наличии дефицита и отрицательный при наличии резерва генерирующей мощности.
Основной технологией идентификации редких событий является использование марковских цепей, где каждое последующее событие определяется на множестве событий, выделенных на предыдущем этапе по некоторому критерию.
Из существующих подходов идентификации редких событий можно выделить два, наиболее приемлемых для технических систем: основанных на использовании технологии вложенных подпространств и преобразовании функций распределения случайных величин (в том числе, энтропийные методы).
Можно отметить, что все рассмотренные процедуры позволяют идентифицировать редкие события с точностью, приемлемой для практического применения. Некоторое предпочтение по критерию робастности можно отдать модифицированному кросс-энтропийному методу из класса преобразований функций распределения.
Точность расчетов во многом зависит от параметров настройки методов, в том числе от объема тестовой выборки на промежуточных этапах формирования значимых событий. При этом длительность расчетов определяется не только объемом выборки, но и необходимостью вероятностных преобразований функций распределения.
Список литературы
Надежность систем энергетики и их оборудования. Спр. в 4 т. / Под общей ред. Ю.Н. Руденко. Т. 2. Надежность электроэнергетических систем. Справочник / Под ред. М.Н. Розанова. М.: Энергоатомиздат, 2000. 568 с.
Руденко Ю.Н., Чельцов М.Б. Надежность и резервирование в энергосистемах. Новосибирск: Наука, 1974.
Обоскалов В.П. Надежность обеспечения баланса мощности электроэнергетических систем. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2002.
Воропай Н.И. Надежность систем энергетики. (Сборник рекомендуемых терминов). М.: ИАЦ “Энергия,” 2007. 192 с.
Чукреев Ю.Я. Сравнение отечественных и зарубежных вероятностных показателей балансовой надежности электроэнергетических систем / Изв. РАН. Энергетика. 2012. № 6. С. 27–37.
Биллинтон Р., Аллан Р. Оценка надежности электроэнергетических систем: пер. с англ. М.: Энергоатомиздат, 1988. 288 с.
Методические указания по проведению расчетов балансовой надежности: СТО 59012820.27.010.005-2018. М.: АО “СО ЕЭС”, 2018. 25 с.
Приказ Министерства энергетики РФ от 6 апреля 2009 г. № 99 “Об утверждении Порядка определения зон свободного перетока электрической энергии (мощности)”: https://base. garant.ru/195834/
Соболь И.М. Метод Монте-Карло. М.: Наука, 1968. 64 с.
Kroese D.P., Taimre T., Botev Z.I. Handbook of Monte Carlo Methods; John Wiley & Sons, Inc.: New Jersey, 2011.
Чукреев Ю.Я. Модели обеспечения надежности электроэнергетических систем. Сыктывкар: Изд-во Коми НЦ УрО РАН, 1995.
Ковалев Г.Ф., Лебедева Л.М. Надежность систем электроэнергетики. Новосибирск: Сибирская издательская фирма “Наука” Академиздатцентра “Наука,” 2015.
Billinton R., Wenyan L. Reliability assessment of electric power systems using Monte Carlo methods; 1st ed.; Springer: New York, 1994.
Обоскалов В.П., Валиев Р.Т. Риск превышения пропускной способности межсистемных связей в задаче балансовой надежности ЭЭС // Изв. РАН. Энергетика. 2018. № 5. С. 3–14.
Чукреев Ю.Я., Полуботко Д.В., Чукреев М.Ю. Применение современных средств параллельных вычислений в информационной системе оценки показателей балансовой надежности электроэнергетических систем // Методические вопросы исследования надежности больших систем энергетики: Вып. 63. Баку: АзНИиПИИЭ, 2013. С. 422–432.
Giuntoli M., Pelacchi P., Poli D. Parallel computing of sequential Monte Carlo techniques for reliable operation of Smart Grids. Proc. – EUROCON 2015, https://doi.org/10.1109/EUROCON.2015.7313707
Martinez J.A., Guerra G. A parallel Monte Carlo method for optimum allocation of distributed generation. IEEE Trans. Power Syst. 2014. V. 29. P. 2926–2933.
Leite da Silva A.M., de Resende L.C., da Fonseca Manso L.A., Miranda V. Composite reliability assessment based on Monte Carlo simulation and artificial neural networks. IEEE Trans. Power Syst. 2007. https://doi.org/10.1109/TPWRS.2007.901302
Singh C., Wang L. Role of artificial intelligence in the reliability evaluation of electric power systems. Turkish J. Electr. Eng. Comput. Sci. 2008.
Pindoriya N.M., Jirutitijaroen P., Srinivasan D., Singh C. Composite reliability evaluation using Monte Carlo simulation and least squares support vector classifier. IEEE Trans. Power Syst. 2011. https://doi.org/10.1109/TPWRS.2011.2116048
Kalinina A., Spada, M., Vetsch D.F., Marelli S., Whealton C., Burgherr P., Sudret B. Metamodeling for Uncertainty Quantification of a Flood Wave Model for Concrete Dam Breaks. mdpi.com, https://doi.org/10.3390/en13143685
Hua B., Bie Z., Au S.K., Li W., Wang X. Extracting rare failure events in composite system reliability evaluation via subset simulation. IEEE Trans. Power Syst. 2015. V. 30. P. 753–762. https://doi.org/10.1109/TPWRS.2014.2327753
Biondini G. An introduction to rare event simulation and importance sampling. Big data analytics. Handbook of statistics, vol. 33. Elsevier; 2015. P. 29–68.222422.
Wang Y., Guo C., Wu Q., Dong S. Adaptive sequential importance sampling technique for short-term composite power system adequacy evaluation. IET Gener. Transm. Distrib. 2014. V. 8. P. 730–741. https://doi.org/10.1049/iet-gtd.2013.0279
Papaioannou I., Papadimitriou C., Straub D. Sequential importance sampling for structural reliability analysis. Struct. Saf. 2016. V. 62. P. 66–75. https://doi.org/10.1016/j.strusafe.2016.06.002
de Boer P.T., Kroese D.P., Mannor S., Rubinstein R.Y. A tutorial on the cross-entropy method. Ann Oper Res. 2005. V. 134(1). P. 19–67.
Yang D.Y., Teng J., Frangopol D.M. Cross-entropy-based adaptive importance sampling for time-dependent reliability analysis of deteriorating structures. Struct Safety. 2017. V. 66. P. 38–50.
Kroese D.P., Rubinstein R.Y., Glynn P.W. Chapter 2 – The cross-entropy method for estimation. Handbook of statistics: machine learning: theory and applications. Handbook of Statistics, vol. 31. Elsevier; 2013. P. 19–34.
Обоскалов В.П., Кокин С.Е., Кирпикова И.Л. Применение вероятностно-статистических методов и теории графов в электроэнергетике / Уч. пособие. Екатеринбург: УрФУ, 2016. 271 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика