Известия РАН. Энергетика, 2021, № 4, стр. 127-139

Методика расчета радиационно-конвективного теплопереноса в высокоэнтальпийном двухфазном потоке в канале энергетической установки

А. М. Руденко¹, В. В. Миронов¹, А. В. Колпаков^1, *

¹ Государственный научный центр Российской Федерации – федеральное государственное унитарное предприятие “Исследовательский центр им. М.В. Келдыша”
Москва, Россия

^* E-mail: a.v.klp@mail.ru

Поступила в редакцию 19.04.2021
После доработки 02.08.2021
Принята к публикации 06.08.2021

DOI: 10.31857/S0002331021040105

Полный текст (PDF)

Аннотация

Ключевые слова: численное моделирование, методика, теплоперенос, излучение, поглощение, рассеяние, высокоэнтальпийный, двухфазный, полидисперсный, поток

ВВЕДЕНИЕ

Скорость нагрева и разрушения стенки канала энергетической установки с заданными термохимическими свойствами определяется суммарным конвективным и радиационным потоком, который является практически наиболее важным параметром радиационно-конвективного взаимодействия и поэтому в первую очередь исследуется при создании современных энергетических установок.

Численное моделирование высокоэнтальпийных излучающих двухфазных потоков связано со значительными трудностями, поэтому исследователи часто рассматривают задачу радиационно-конвективного взаимодействия в упрощенной постановке, когда влиянием того или иного фактора на решение можно пренебречь.

В [1] для простой геометрии (плоская стенка) предложена методика расчета и получено численное решение для радиационного прогрева и разрушения теплозащитного композиционного материала в вакууме при наличии радиационно-конвективного взаимодействия в сверхзвуковом осесимметричном двухфазном эрозионном факеле, содержащем поглощающие и рассеивающие частицы. Показано, что учет дивергенции потока излучения в уравнении энергии приводит к перестройке расчетного поля течения, в частности, поглощение излучения приводит к сильному нагреву двухфазного потока, однако, это практически не влияет на поток излучения в разрушающуюся стенку и на скорость ее прогрева.

В [2] получены численные оценки радиационных потерь в перспективном алюмоводородном реакторе для рабочих температур на уровне 3000 К и выше. В рабочей зоне такого реактора присутствуют частицы водяного пара и алюминия, которые активно участвуют в радиационном теплообмене, так что радиационные потери на стенках реактора могут быть сопоставимы с генерируемой мощностью, и поэтому возможность практической реализации генератора становится не очевидной, а оценки радиационных потерь критически важными. Задача о радиационно-конвективном взаимодействии в данном случае также решалась в простой одномерной постановке для однородной среды, свойства которой не зависят от координат и являются задаваемым параметром.

В [3] исследовано влияние столкновений частиц на расчетный поток излучения при натекании сверхзвукового двухфазного потока на препятствие. Также рассматривалась простая геометрия – натекание на шар. Решение аналогичной задачи для потока в канале сложной геометрии при наличии разрушающейся под действием теплового потока стенки связано, очевидно, с существенно большими трудностями.

Методические основы организации численного моделирования теплопереноса в высокоэнтальпийных, неравновесных по температуре и по скорости турбулентных двухфазных потоках при наличии областей дозвукового и сверхзвукового течения с целью определения теплового потока в разрушающуюся стенку энергетического канала сложной геометрии были даны в ГНЦ ФГУП “Центр Келдыша” (см. [4–6]). Эти исследования получили затем развитие в [7–9]. Влияние поглощения и рассеяния теплового излучения частицами дисперсной фазы в этих работах не учитывалось.

В [5, 6] предложен метод расчета трехмерных двухфазных вязких течений вблизи затупленных тел или при вдуве поперечных струй со скачками уплотнения и дозвуковыми зонами, приведены примеры расчета трехмерных вихревых течений, выполнено сравнение с экспериментов по давлению, плотности и геометрии скачков. Тестирование программы выполнялось путем сопоставления с известными решениями для течения Прандтля–Майера и для натекания потока на клин. Использовались метод установления, нестационарные уравнения Навье–Стокса для идеального газа и двухслойная модель турбулентности Болдуина–Ломакса–Ван Дриста.

Результаты [5] были развиты в [6] для случая трехмерных течений в соплах ракетных двигателей, было выполнено сравнение с экспериментом по локальным и интегральным параметрам, которое показало хорошее согласие с расчетными данными. Нестационарные уравнения записывались в прямоугольной системе координат, для коэффициента турбулентной вязкости использовались разные соотношения во внутренней и внешней областях, решение находилось в результате применения метода крупных частиц и разностной схемы с механизмом диссипации для сглаживания разрывов, использование адаптивных сеток было признано не целесообразным. Указывается, что традиционные методы характеристик и установления в рассмотренном случае течения не применимы, потому что не позволяют моделировать до- и трансзвуковые течения при наличии в потоке областей с сильными разрывами.

Целью данной работы является создание на основе результатов и опыта численных исследований [4–9], выполненных в ГНЦ ФГУП “Центр Келдыша”, единой методики расчета и соответствующей программы для численного моделирования радиационно-конвективного теплопереноса в высокоэнтальпийном двухфазном потоке продуктов сгорания с областями до- и сверхзвукового течения. Рассматриваются энергетические каналы сложной, изменяющейся со временем геометрией при наличии широкого спектра взаимосвязанных физических процессов в двухфазном потоке продуктов сгорания: вязкости, теплопроводности, турбулентности, излучения и поглощения теплового излучения стенками, поглощения и рассеяния полидисперсными частицами конденсированной фазы, деструкции и химической абляции.

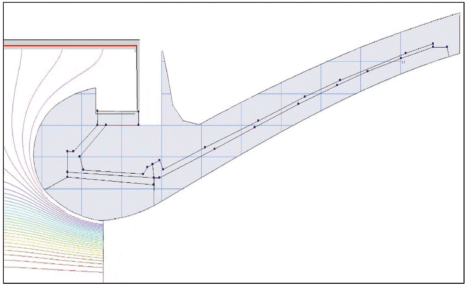
Схема расчетной области показана на рис. 1. Двухфазный поток движется слева направо, разгоняясь от дозвуковой скорости до скорости, которая в несколько раз превышает скорость звука. Перед входом в сужающуюся часть канала имеется “карман” со сложной геометрией границы, течение в котором происходит с дозвуковой скоростью.

Рис. 1.

Схема расчетной области.

МОДЕЛИРОВАНИЕ ТЕЧЕНИЯ ДВУХФАЗНОЙ СРЕДЫ

Полная система уравнений для численного моделирования радиационно-конвективного прогрева стенки энергетического канала включает:

– уравнения нестационарной газовой динамики для совершенного газа в цилиндрической системе координат в двумерной постановке;

– уравнения движения частиц продуктов сгорания;

– уравнения сжимаемого турбулентного пограничного слоя в интегральной форме;

– уравнение переноса излучения в двухфазной смеси продуктов сгорания;

– уравнение теплопроводности для стенки сопла;

– уравнения, описывающие унос массы материала стенки из-за взаимодействия с продуктами сгорания и термодеструкции связующего материала.

Законы сохранения массы, компонент импульса и энергии для газовой фазы:

(1)

$\frac{{\partial (y~\rho )}}{{\partial t}} + ~\nabla ~\left( {y~\rho ~U} \right) = ~0,$

(2)

$\frac{{\partial (y~\rho ~u)}}{{\partial t}} + \nabla ~\left( {y~\rho ~u~U} \right) + \frac{{\partial (y~P)}}{{\partial x}} = y~\sum\limits_{i = 1}^l {{{\rho }_{i}}~C{{r}_{{i~}}}~({{u}_{{i~}}} - u)} ,$

(3)

$\frac{{\partial (y~\rho ~{v})}}{{\partial t}} + \nabla ~\left( {y~\rho {v}U} \right) + \frac{{\partial (yP)}}{{\partial y}} = y\sum\limits_{i = 1}^l {{{\rho }_{i}}~C{{r}_{{i~}}}~({{{v}}_{{i~}}} - {v})} ,$

(4)

$\frac{{\partial (y\rho E)}}{{\partial t}} + \nabla ~\left( {y\rho EU} \right) = y~\sum\limits_{i = 1}^l {{{a}_{i}}~C~\left( {{{T}_{{i~}}}--T} \right)} + C{{r}_{{i~}}}({{u}_{{i~}}}\left( {{{u}_{{i~}}} - u} \right) + {{{v}}_{{i~}}}\left( {{{{v}}_{{i~}}} - {v}} \right)),$

(5)

$E = h + ~{{({{u}^{2}} + {{{v}}^{2}})} \mathord{\left/ {\vphantom {{({{u}^{2}} + {{{v}}^{2}})} 2}} \right. \kern-0em} 2}.$

Законы сохранения массы, компонент импульса и энергии для конденсированной фазы (лагранжево представление процессов коагуляции и дробления частиц):

(6)

$\nabla ~\left( {y{{\rho }_{i}}{{U}_{i}}} \right) = y\left( {{{n}_{i}}\sum\limits_{j = 1}^{i - 1} {{{K}_{{ji}}}{{{\text{Ф}}}_{{ji}}}{{\rho }_{j}} - {{\rho }_{i}}} \sum\limits_{j = i + 1}^l {{{K}_{{ij}}}{{{\text{Ф}}}_{{ij}}}{{n}_{j}}} } \right),$

(7)

$\nabla ~\left( {y{{n}_{i}}{{U}_{i}}} \right) = - y{{n}_{i}}\sum\limits_{j = i + 1}^l {{{K}_{{ij}}}{{{\text{Ф}}}_{{ij}}}{{n}_{j}}} ,$

(8)

$\begin{gathered} \nabla ~\left( {y{{\rho }_{i}}{{u}_{i}}{{U}_{i}}} \right) = y{{\rho }_{i}}C{{r}_{i}}~\left( {u - {{u}_{i}}} \right) + y{{n}_{i}}\left( {\sum\limits_{j = 1}^{i - 1} {({{K}_{{ji}}}{{\rho }_{j}}\left( {{{u}_{j}}--{{u}_{i}}} \right) + {{{\text{Ф}}}_{{ji~}}}{{u}_{i}}) + y{{\rho }_{i}}} } \right.~ \times \\ \times \,\,\left( {\sum\limits_{j = i + 1}^l {{{K}_{{ij}}}{{n}_{j}}~\left( {1 - {{{\text{Ф}}}_{{ij~}}}} \right)\left( {{{u}_{{j~}}}--{{u}_{{i~}}}} \right) - {{{\text{Ф}}}_{{ji~}}}{{u}_{i}}} } \right), \\ \end{gathered} $

(9)

$\begin{gathered} \nabla ~\left( {y{{\rho }_{i}}{{{v}}_{i}}{{U}_{i}}} \right) = y{{\rho }_{i}}C{{r}_{{i~}}}~\left( {{v} - {{{v}}_{{i~}}}} \right) + y{{n}_{i}}\left( {\sum\limits_{j = 1}^{i - 1} {({{K}_{{ji}}}{{\rho }_{j}}~\left( {{{{v}}_{j}}--{{{v}}_{i}}} \right) + {{{\text{Ф}}}_{{ji~}}}{{{v}}_{i}}} } \right) + \\ + \,\,y{{\rho }_{i}}~\left( {\sum\limits_{j = i + 1}^l {{{K}_{{ij}}}{{n}_{j}}\left( {1 - {{{\text{Ф}}}_{{ij}}}} \right)\left( {{{{v}}_{j}}--{{{v}}_{i}}} \right) - {{{\text{Ф}}}_{{ji}}}{{{v}}_{i}}} } \right), \\ \end{gathered} $

(10)

$\begin{gathered} \nabla ~\left( {y{{\rho }_{i}}{{C}_{s}}{{T}_{i}}{{U}_{i}}} \right) = y{{\rho }_{i}}\left( {~{{a}_{i}}C~\left( {T - {{T}_{i}}} \right) - C{{r}_{{i~}}}\left( {{{u}_{{i~}}}\left( {{{u}_{{i~}}} - u} \right) + {{{v}}_{{i~}}}\left( {{{{v}}_{i}} - {v}} \right)} \right)} \right) + ~y~{{n}_{i}}\sum\limits_{j = 1}^{i - 1} {{{K}_{{ji}}}} \times \\ \times \,\,{{\rho }_{j}}~\left( {{{E}_{j}}--\left( {1 - {{{\text{Ф}}}_{{ji~}}}} \right){{E}_{i}}} \right) - y~{{\rho }_{i}}~\sum\limits_{j = i + 1}^l {{{K}_{{ij}}}{{n}_{j}}~\left( {{{E}_{{i~}}}--\left( {1 - {{{\text{Ф}}}_{{ij~}}}} \right){{E}_{{j~}}}} \right) + \nabla {{q}_{{rad}}}~} , \\ \end{gathered} $

(11)

${{E}_{{j~}}} = {{C}_{s}}~{{T}_{j}} + {{U_{j}^{2}} \mathord{\left/ {\vphantom {{U_{j}^{2}} 2}} \right. \kern-0em} 2}.$

Соотношения для коэффициента коагуляции, эффективности столкновений и для коэффициента захвата частиц:

${{K}_{{ij}}} = \pi {{({{r}_{{i~}}} + {{r}_{{j~}}})}^{2}}\left| {~{{{\mathbf{U}}}_{i}} - {\mathbf{~}}{{{\mathbf{U}}}_{j}}} \right|{{{\text{Э}}}_{{ij~}}},$

${{{\text{Э}}}_{{ij}}} = \frac{{60{{{{{\hat {э}}}}}_{{ij}}} + {\text{R}}{{{\text{e}}}_{j}}{{{\mathop {\text{э}}\limits^ \vee }}_{{ij}}}}}{{60 + {\text{R}}{{{\text{e}}}_{j}}}},$

${{{{\hat {э}}}}_{{ij}}} = {{\left( {1 + \frac{{0.75\ln \left( {4~S{{t}_{{ij}}}} \right)}}{{2~S{{t}_{{ij}}} - 1.214}}} \right)}^{{ - 2}}}\,\,{\text{при}}\,\,S{{t}_{{ij}}} > 0.607,$

${{\mathop {\text{{\vэ}}}}_{{ij~}}} = {{\left( {\frac{{{\text{S}}{{{\text{t}}}_{{ij}}}}}{{~{\text{S}}{{{\text{t}}}_{{ij}}} + 0.125}}} \right)}^{2}}\,\,{\text{при}}\,\,{\text{S}}{{{\text{t}}}_{{ij}}} > 0.0417,$

${\text{Число}}\,\,{\text{Стокса}}\,\,{\text{S}}{{{\text{t}}}_{{ij}}} = ~\frac{{\left| {{{U}_{i}} - ~~{{U}_{j}}} \right|d_{i}^{2}{{\rho }_{{{\text{в}}i}}}}}{{9~{{d}_{j}}{{\mu }_{g}}}}\,\,{\text{при}}\,\,{{r}_{j}} > {{r}_{i}},$

$\begin{gathered} {{{\text{Ф}}}_{{ij~}}} = 1 - \left( {0.247~{\text{Re}}_{{ij}}^{{0.434}}~{\text{Lp}}_{j}^{{ - 0.133}}~{{{\left( {\frac{{{{r}_{{i~}}}}}{{{{r}_{{j~}}}}}} \right)}}^{{0.273}}} + 0.18{\text{Re}}_{{ij}}^{{0.395}}{\text{Lp}}_{j}^{{0.117}}~{{{\left( {\frac{{{{r}_{{i~}}}}}{{{{r}_{{j~}}}}}} \right)}}^{{2.27}}}{\text{We}}_{i}^{{0.67}}} \right) \\ {\text{при}}\,\,{{r}_{{j~}}} > {{r}_{{i~}}}, \\ \end{gathered} $

${\text{Число}}\,\,{\text{Рейнольдса}}\,\,{\text{R}}{{{\text{e}}}_{{ij}}} = \frac{{\left| {{{{\mathbf{U}}}_{i}} - {{{\mathbf{U}}}_{j}}} \right|{{d}_{i}}{{\rho }_{{{\text{в}}i}}}}}{{{{\mu }_{{{\text{в}}i}}}}},$

${\text{Число}}\,\,{\text{Вебера}}\,\,{\text{W}}{{{\text{e}}}_{i}} = \frac{{~{{{\left| {{{{\mathbf{U}}}_{i}} - {{{\mathbf{U}}}_{j}}} \right|}}^{2}}{{d}_{i}}{{\rho }_{g}}}}{{{{\sigma }_{{{\text{в}}i}}}}},$

${\text{Число}}\,\,{\text{Лапласа}}\,\,{\text{L}}{{{\text{p}}}_{j}} = {{\left( {\frac{{~\mu _{{\text{в}}}^{2}~}}{{{{d}_{j}}~{{\rho }_{{{\text{в}}j~}}}{{\sigma }_{{{\text{в}}j}}}}}} \right)}^{{ - 1}}}.$

Соотношения для коэффициентов сопротивления и теплообмена:

$C{{r}_{i}} = ~\frac{{3~\rho ~\left| {U - ~~{{U}_{i}}} \right|~}}{{4~{{\rho }_{{{\text{в}}i}}}~{{d}_{i}}}}~\frac{{24}}{{{\text{R}}{{{\text{e}}}_{i}}}}~{{\varphi }_{{40}}},$

${{\varphi }_{{40}}} = 1 + 0.15~{\text{Re}}_{{{\text{Wi}}}}^{{0.687}},$

${\text{R}}{{{\text{e}}}_{{wi}}} = {\text{R}}{{{\text{e}}}_{i}}(1 + 0.03~{\text{W}}{{{\text{e}}}_{i}}),$

${\text{W}}{{{\text{e}}}_{i}} = ~\frac{{~{{{\left| {U - ~~{{U}_{i}}} \right|}}^{2}}~{{d}_{i}}{{\rho }_{i}}}}{{{{\sigma }_{i}}}},$

${{\varphi }_{4}} = \frac{{{{\varphi }_{{40}}}}}{{1 - 0.1615~\sqrt {k~} ~\frac{{{\text{R}}{{{\text{e}}}_{{wi}}} - 24}}{{{\text{R}}{{{\text{e}}}_{i}}}}~{{\varphi }_{{40}}}{{M}_{i}}~~}}~~\,\,{\text{для\;R}}{{{\text{e}}}_{{wi}}} < 24,$

${{\varphi }_{4}} = {{\varphi }_{{40}}} + 0.00299~\frac{{({\text{R}}{{{\text{e}}}_{{wi}}} - 24)~{\text{R}}{{{\text{e}}}_{i}}}}{{24~~}}{{M}_{i}}\,\,{\text{для}}\,\,24 < {\text{R}}{{{\text{e}}}_{{wi}}} < 100,$

${{\varphi }_{4}} = {{\varphi }_{{40}}} + 0.00079~\frac{{({\text{R}}{{{\text{e}}}_{{wi}}} + 187.6)~{\text{R}}{{{\text{e}}}_{i}}}}{{24}}{{M}_{i}}\,\,{\text{для}}\,\,{\text{R}}{{{\text{e}}}_{{wi}}} > 100,$

${{M}_{{i~}}} = \frac{{\left| {U - ~~{{U}_{i}}} \right|~}}{a}$ – число Маха $C{{a}_{i}} = 6{\text{N}}{{{\text{u}}}_{i}}~\frac{{~\lambda }}{{d_{i}^{2}}}$

${\text{N}}{{{\text{u}}}_{i}} = \frac{{~{\text{N}}{{{\text{u}}}_{{0~~}}}}}{{1 + {{3.42{{M}_{i}}{\text{N}}{{{\text{u}}}_{0}}} \mathord{\left/ {\vphantom {{3.42{{M}_{i}}{\text{N}}{{{\text{u}}}_{0}}} {({\text{R}}{{{\text{e}}}_{i}}{\text{Pr}})}}} \right. \kern-0em} {({\text{R}}{{{\text{e}}}_{i}}{\text{Pr}})}}}},$

${\text{N}}{{{\text{u}}}_{0}} = 2 + 0.459{\text{Re}}_{i}^{{0.55}}{\text{P}}{{{\text{r}}}^{{0.33}}}.$

Выражение для Ф_ij справедливо в широком диапазоне параметров:

$35 < {{\operatorname{Re} }_{{ij}}} < 385;\,\,\,0.00167 < {\text{L}}{{{\text{p}}}_{j}} < 0.2;\,\,\,0.083 < \left( {{{r}_{i}}/{{r}_{j}}} \right) < 0.5.$

Аэродинамическое дробление частиц определяется числом Вебера. Применяется модель дробления на два равных осколка при достижении числом Вебера критического значения ${\text{We}} = 17.$ Диаметр частиц данной фракции в результате дробления уменьшается в $\sqrt[3]{2}$ раз, а концентрация удваивается.

УРАВНЕНИЕ ПЕРЕНОСА ТЕПЛОВОГО ИЗЛУЧЕНИЯ

При необходимости поток теплового излучения к стенке канала энергетической установки может быть определен с использованием точных методов, одним из которых является метод статистических испытаний Монте-Карло [8–10]. Примеры использования метода Монте-Карло для расчета потока излучения от продуктов сгорания ракетных двигателей приведены в [8, 9]. Такие расчеты, как и в случае применения других “точных” методов [10], занимают значительное время.

Когда перенос тепла излучением является, наряду с теплопроводностью и конвекцией, одним из способов комбинированного теплопереноса, и для численного решения полной системы уравнений теплообмена требуется большое количество компьютерного времени, используются относительно простые приближенные методы расчета, одним из которых является Р₁-приближение [11, 12].

Точность расчета переноса излучения в Р₁-приближении достаточно высока в областях медленного, дозвукового движения высокоэнтальпийного двухфазного потока, там, где параметры медленно меняются в зависимости от координат, среда является оптически толстой, а поток излучения сопоставим с конвективным тепловым потоком (см. [10]). В областях сверхзвукового движения оптическая толщина среды относительно мала, и погрешность расчета потока излучения в Р₁-приближении становится больше, но при этом конвективный тепловой поток значительно превышает поток излучения, так что погрешность расчета суммарного потока энергии, которым определяется нагрев, унос и деструкция материала канала (см. [10]), не велика. Время расчета в Р₁-приближении относительно мало, что, вместе с приемлемой для практических задач точностью, делает это приближение востребованным при численном моделировании радиационно-конвективного взаимодействия.

Решение уравнения Р₁-приближения с соответствующим граничным условием сводится к решению граничной задачи переноса тепла теплопроводностью. Использование транспортного приближения для индикатрисы рассеяния позволяют учесть анизотропное рассеяние, поглощение и тепловое излучение частицами.

(12)

$ - \nabla \left( {D\nabla g} \right) + {{K}_{{abs}}}g = 4{{K}_{{abs}}}~\sigma ~{{T}^{4}},\,\,\,\,D = {1 \mathord{\left/ {\vphantom {1 {(3\left( {{{K}_{{abs}}} + {{K}_{{sca}}}} \right))}}} \right. \kern-0em} {(3\left( {{{K}_{{abs}}} + {{K}_{{sca}}}} \right))}}.$

Коэффициенты поглощения и транспортного ослабления частиц рассчитываются по известной функции распределения по радиусу [3]:

(13)

${{K}_{{abs}}} = 0.75~\frac{{{{f}_{{v}}}}}{{{{a}_{{30}}}}}\int\limits_0^\infty {~{{Q}_{{abs}}}{{a}^{2}}F\left( a \right)da} ,\,\,\,\,{{K}_{{sca}}} = 0.75~\frac{{{{f}_{{v}}}}}{{{{a}_{{30}}}}}\int\limits_0^\infty {{{Q}_{{sca}}}{{a}^{2}}F\left( a \right)da} ,$

(14)

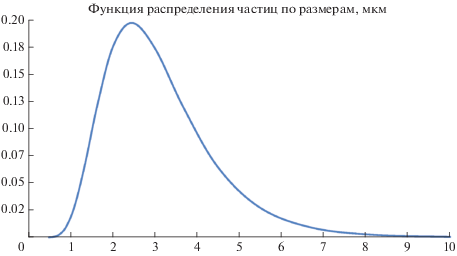
$\int\limits_0^\infty {F\left( a \right)da} = 1,\,\,\,\,{{f}_{{v}}} = \frac{{4\pi }}{3}{{N}_{p}}~\int\limits_0^\infty {{{a}^{3}}F\left( a \right)da} ,\,\,\,\,{{a}_{{ij}}} = \frac{{\int\limits_0^\infty {{{a}^{i}}F\left( a \right)da} }}{{\int\limits_0^\infty {{{a}^{j}}F\left( a \right)da} }}.$

Характерная функция распределения частиц по размерам показана на рис. 2.

Рис. 2.

Функция распределения частиц по радиусу (мкм).

Для экономии времени расчета спектральные и температурные зависимости действительной и мнимой частей показателя преломления Al₂O₃, а также факторов эффективности поглощения и транспортной экстинкции определяются по инженерным формулам [3]. Коэффициенты поглощения газовой фазы определяются как в [13–16].

В осесимметричной постановке:

(15)

$\frac{{\partial \left( {D\frac{{\partial g}}{{\partial x}}} \right)}}{{\partial x}} + \frac{{\partial \left( {D\frac{{\partial g}}{{\partial r}}} \right)}}{{\partial r}} + \frac{D}{r}\frac{{\partial g}}{{\partial r}} - {{K}_{a}}g = - 4{{K}_{a}}\sigma T_{p}^{4}.$

Для перехода к прямоугольной расчетной области используется замена переменных:

$\left\{ {\begin{array}{*{20}{c}} {\eta = x} \\ {\zeta = \frac{r}{{R\left( x \right)}}} \end{array}} \right.;\,\,\,\,\left\{ {\begin{array}{*{20}{c}} {x = \eta } \\ {r = \zeta R\left( \eta \right)} \end{array}} \right.,\,\,\,\,\left\{ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}} = \frac{\partial }{{\partial \eta }} - \frac{\zeta }{R}\frac{{dR(x)}}{{dx}}\frac{\partial }{{\partial \zeta }}} \\ {\frac{\partial }{{\partial r}} = \frac{1}{{R(x)}}\frac{\partial }{{\partial \zeta }}} \end{array}} \right..$

НАЧАЛЬНОЕ И ГРАНИЧНЫЕ УСЛОВИЯ

На входном сечении задается условие скоростного и температурного равновесия между газовой фазой и частицами. На твердой границе используется условие равенства нулю всех компонент скорости, на оси симметрии – условие равенства нулю нормальной компоненты скорости. На открытых границах, через которые поток вытекает, используется, в соответствии с выводами [2], линейная интерполяция. На границе, через которую втекает сверхзвуковой поток, задаются параметры, соответствующие этому потоку, которые остаются неизменными в ходе вычислений. Для дозвукового потока задаются направление скорости, давление и температура торможения. Если направление потока заранее не известно, или потоки малы по величине, то на открытой границе в фиктивные ячейки на каждом шаге по времени заносятся значения параметров из соседних ячеек.

В результате решения задачи переноса излучения определяется радиационный тепловой поток в стенку. В качестве граничного условия используется текущее расчетное распределение температуры стенки ${{T}_{w}}.$

Граничное условие для Р₁-приближения:

(16)

$ - D\frac{{\partial g}}{{\partial n}} = {{\gamma }_{w}}\left( {{{g}_{w}} - 2\sigma T_{w}^{4}} \right),$

производная берется по внешней нормали, ${{T}_{w}}$ – температура границы, ${{\gamma }_{w}} = \frac{{{{\varepsilon }_{w}}}}{{\left( {2 - {{\varepsilon }_{w}}} \right)}},$ ${{\varepsilon }_{w}}$ – степень черноты границы.

В качестве начальных условий могут быть использованы известные аналитические решения для одномерного течения в канале.

МЕТОДИКА РАСЧЕТА

Решение для смешанного невязкого и нетеплопроводного течения продуктов сгорания определяется при помощи метода установления. Используется стационарный аналог нецентральной конечно-разностной схемы Мак-Кормака второго порядка точности. Для сверхзвуковых областей течения уравнения записываются в дивергентной форме и решаются методом сквозного счета с использованием явной двухшаговой разностной схемы и сглаживания.

Интегрирование системы уравнений для частиц конденсированной фазы осуществляется с помощью неявной разностной схемы, имеющей второй порядок точности. Расчет движения частиц производится с использованием схемы второго порядка точности типа с адаптивным выбором шага интегрирования, в предположении о равномерном предиктор-корректор распределении частиц по радиусу на входе в сопло, по известному газовому полю. Интегральные параметры движения и траектории находятся по экспериментальному спектру массового распределения частиц по размерам. Для интегрирования системы дифференциальных уравнений, описывающих движение частиц, их правые части на каждом шаге линеаризуются и определяется их аналитическое решение, что позволяет сохранить высокую точность результата для мелких частиц, когда уравнения движения содержат члены с малым коэффициентом при производной высшего порядка.

Расчет параметров турбулентного пограничного слоя, энтальпии восстановления, а также нестационарного теплового состояния и уноса материалов стенки выполняются сопряженно для найденного предварительно поля течения невязкого газа с частицами.

Вычисления организуются в следующей последовательности:

– из решения системы уравнений течения двухфазной среды при заданной температуре стенки для стационарного режима определяются поля течения и конвективный тепловой поток в стенку;

– по известному полю концентрации частиц и полю температуры частиц конденсированной фазы определяется поток излучения в стенку (решение уравнения переноса излучения);

– определяются распределения температуры в сечениях по длине стенки и параметры разрушения материала для заданных моментов времени (коэффициент тепломассообмена пересчитывается в зависимости от текущей температуры поверхности стенки);

– температура поверхности с предыдущего приближения используется для расчета параметров течения двухфазной среды и радиационного потока в последующих приближениях.

ТЕСТИРОВАНИЕ

Тестирование блока расчета течения осуществлялось путем сравнения с решениями для осесимметричного сопла, полученными методом крупных частиц, Мак-Кормака и методом характеристик, для распределения числа Маха по стенке сопла. Отличие составило менее 3%. Заметная разница в результатах расчета имела место лишь в области резкого разгона потока сразу за критическим течением. Также выполнено сравнение с известными решениями для течения Прандтля–Майера и для натекания на клин и с результатами эксперимента. Для истечения из сопла в диффузор продемонстрировано качественное совпадение картины течения с наблюдаемой экспериментально, при этом расчетная зависимость давления от осевой координаты отличается от экспериментальных данных не более чем на 25–30%.

Тестирование решения в Р₁–приближении осуществлялось путем сравнения с аналитическим решением для двумерной осесимметричной задачи и с решением по методу Монте Карло, подробное описание результатов сравнения можно найти в [8, 11, 12].

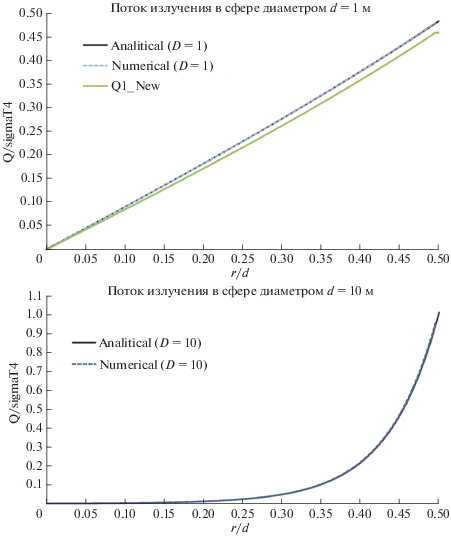
На рис. 3а и 3б приведены примеры сравнения расчета в Р₁-приближении методом конечных разностей с аналитическими решениями для коэффициента поглощения 1 1/м при отсутствии рассеяния. Видно, что отличие не превышает 1%. (Линия Q1_New соответствует DP₀-приближению).

Рис. 3.

Сравнение расчета в Р₁-приближении с аналитическими решениями.

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Приведем примеры расчета радиационно-конвективного теплообмена применительно к задаче прогрева соплового блока ракетного двигателя высокотемпературным двухфазным потоком продуктов сгорания твердого топлива.

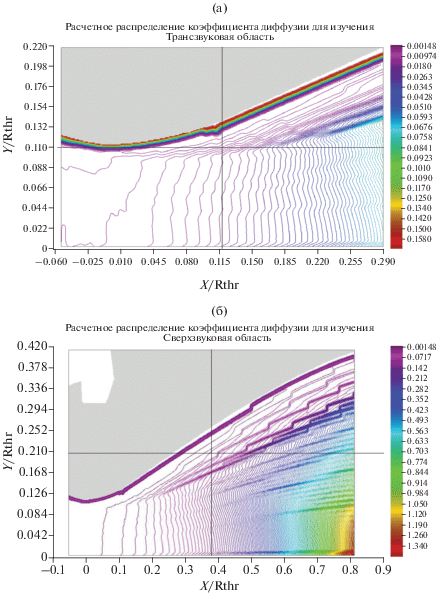
Функция распределения частиц по радиусу показана на рис. 2. Коэффициенты поглощения и рассеяния определялись по полям концентрации и температуры частиц, найденным в результате газодинамического расчета для известной функции распределения, с использованием соотношений теории Ми или инженерных формул, аппроксимирующих эти соотношения. Расчетное распределение коэффициента диффузии излучения $D$ представлено на рис. 4.

Рис. 4.

Пример распределения расчетных значений коэффициента диффузии излучения.

В дозвуковой зоне, где плотность частиц конденсированной фазы велика, коэффициент диффузии излучения мал – находится на уровне 0.003 м, что соответствует коэффициенту ослабления ~100 1/м, поток излучения в этой части канала также мал. За критическим сечением, в сверхзвуковой зоне концентрация частиц в потоке уменьшается, и коэффициент излучения увеличивается почти на 2 порядка до 0.3–0.5 м соответственно, поток излучения также увеличивается. В пристеночной области, в которой частицы практически отсутствуют, коэффициент диффузии возрастает до значений существенно больше 1.

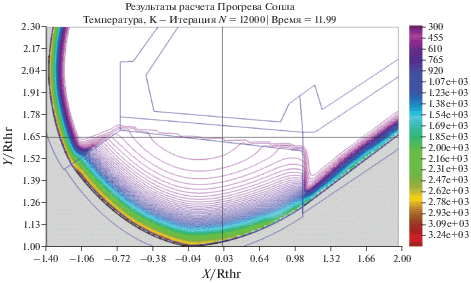
Пример расчетного распределения температуры в некоторый момент времени в стенке соплового блока показано на рис. 5.

Рис. 5.

Распределение температуры в стенке канала (t = 12 с).

Результаты расчета величин конвективного и радиационного теплового потока вдоль образующей канала для разных моментов времени показаны на рис. 6.

Рис. 6.

Расчетные зависимости радиационного и конвективного тепловых потоков вдоль образующей канала.

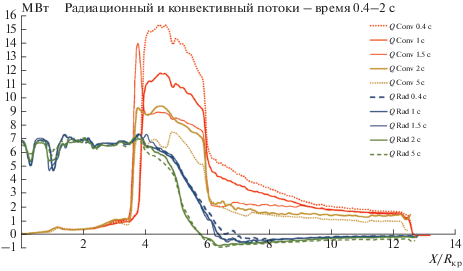
Как видно по рис. 6, конвективный поток в стенку канала максимален в области критического сечения, там, где он составляет 11–15 МВт/м² и в 2–2.5 раза превышает поток излучения, так что максимальная тепловая нагрузка реализуется в области критического течения и определяется, в основном, конвективным подводом энергии к стенке. В области дозвукового течения тепловая нагрузка определяется излучением: поток излучения в 6–7 раз больше конвективного потока, находится на уровне 6 МВт/м² и слабо зависит от времени. В области сверхзвукового течения поток излучения отрицателен, т.е. имеет место отток энергии от стенки посредством излучения, причем величина этого оттока составляет 20–30% от конвективного потока к стенке (радиационное охлаждение).

ВЫВОДЫ

Разработана алгоритмически единая методика расчета, и на ее основе создана комплексная программа для численного моделирования радиационно-конвективного теплопереноса в высокоэнтальпийном двухфазном потоке продуктов сгорания в осесимметричном канале энергетической установки со сложной геометрией разрушающейся стенки при наличии областей дозвукового и сверхзвукового течения. В расчетной модели учитывается широкий спектр взаимосвязанных физических процессов: вязкость, теплопроводность, турбулентность, излучение и поглощение теплового излучения стенками и полидисперсными частицами конденсированной фазы, деструкция и химическая абляция. Приведены примеры расчетов теплового потока с учетом вязкости, теплопроводности, турбулентности течения, поглощения и анизотропного рассеяния теплового излучения.

ОБОЗНАЧЕНИЯ

u_i, v_i – компоненты вектора скорости U_i частиц i-й фракции; u, v – компоненты вектора скорости $U$ газа; x, y – осевая и радиальная координаты; C, C_i – удельные теплоемкости газа и материала частиц i-й фракции; ρ – плотность газа; P – давление газа; h – энтальпия газа; T – температура газа; E – полная энергия газа; γ – показатель адиабаты газа; n_i – число частиц i-й фракции в единице объема; r_i – радиус частиц i-й фракции; ${{M}_{{i~}}}$ – число Маха; L_pi – число Лапласа; Nu_i – число Нуссельта; We_i – число Вебера; Re_ij – число Рейнольдса; Cr_i – коэффициент сопротивления; K_ij – константа коагуляции; Э_ij – коэффициент эффективности соударений (коэффициент захвата); Ф_ij – коэффициент коагуляции; ρ_в – плотность материала частиц конденсированной фазы; µ – вязкость газовой фазы; µ_в – вязкость материала конденсированной фазы; F(a) – функция распределения частиц по радиусу; Q_a, Q_sca, Q_ext – факторы эффективности поглощения, транспортного рассеяния и ослабления; k_abs, k_sca, k_ext – коэффициенты поглощения, транспортного рассеяния и ослабления; D – коэффициент диффузии излучения; g – плотность энергии излучения; ${{q}_{{rad}}}$ – вектор потока излучения; $\nabla $ – векторный дифференциальный оператор набла.

Список литературы

Dombrovsky L.A., Yukina E.P., Kolpakov A.V., Ivanov V.A. Procedure for calculating the thermal destruction of phenolic carbon under the effect of intensive infrared radiation. – High Temperature. 1993. T. 31. № 4. C. 566.
Bityurin V.A., Galaktionov A.V., Kolpakov A.V. Reducing radiative losses in aluminum–hydrogen MHD generators. – Technical Physics Letters. 2010. V. 36. № 11. P. 1046–1048.
Reviznikov D.L., Sposobin A.V., Dombrovsky L.A. Computational analysis of radiative heat transfer from supersonic flow with suspended polydisperse particles to a blunt body. – Proceedings of CHT-15 ICHMT International Symposium on Advances in Computational Heat Transfer May 25–29, 2015, Rutgers University, Piscataway, USA.
Губертов А.М., Миронов В.В., Борисов Д.М. и др. Газодинамические и теплофизические процессы в ракетных двигателях твердого топлива. М.: Машиностроение, 2004.
Борисов Д.М., Горшков В.Е. Метод расчета трехмерных двухфазных вязких течений вблизи затупленных тел или при вдуве поперечных струй. – Математическое моделирование. 1996. Т. 8. № 6. С. 38–46.
Борисов Д.М., Васютичев А.С., Лаптев И.В., Руденко А.М. Численное моделирование трехмерных смешанных вязких течений с ударными волнами. – Математическое моделирование. 2007. Т. 19. № 11. С. 112–120.
Борисов Д.М., Шураев Ю.А., Миронов В.В., Руденко А.М. Метод расчета теплового состояния сопловых насадков энергодвигательных установок. – Известия РАН. Энергетика. 2012. № 5. С. 104–109.
Ковалкин С.С., Колпаков А.В., Миронов В.В. Применение метода Монте–Карло для расчета переноса энергии излучением в каналах энергетических установок. – Известия Российской академии наук. Энергетика. 2012. № 4. С. 90–98.
Гурина И.Н., Волкова Л.И., Волков Н.Н., Ковалкин С.С., Колпаков А.В., Миронов В.В. Использование численного моделирования радиационно-конвективного теплообмена для оценки применимости экспериментальных результатов, полученных в установке для высотных испытаний современных жидкостных ракетных двигателей, к реальным условиям их работы. – В сборнике: Труды Шестой Российской национальной конференции по теплообмену 2014. С. 1198–1201.
Viskanta R., Menguc M.P. Radiation heat transfer in combustion systems. Prog. Energy Combust. Sci. 1987. V. 13. P. 97–160.
Домбровский Л.А., Баркова Л.Г. Решение двумерной задачи переноса теплового излучения в анизотропно рассеивающей среде. – ТВТ. 1986. Т. 24. Вып. 4. С.762–769.
Kolpakov A.V., Dombrovsky L.A., Surzhikov S.T. An approximate method for calculating the transfer of directional emission in an absorbing and anisotropically scattering medium. – Teplofizika vysokih temperatur. 1990. V. 28. № 5. (In Russian)
Bohren C.F., Huffman D.R. Absorption and Scattering of Light by Small Particles. N.Y.: Wiley, 1983. 530 p.
Каменщиков В.А.; Пластинин Ю.А.; Николаев В.М. и др. Радиационные свойства газов при высоких температурах. М.: Машиностроение, 1971. 440 с.
Суржиков С.Т. Оптические свойства газов и плазмы. – Изд. МГТУ им. Н.Э.Баумана. 2004. 576 с.
https://www.cfa.harvard.edu/hitran/

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал