Известия РАН. Энергетика, 2022, № 1, стр. 47-56
Расчет грозовых перенапряжений воздушных линий с импульсной короной в цепных схемах
С. Л. Шишигин 1, *, Д. С. Шишигин 1, И. Н. Смирнов 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
Вологодский государственный университет
Вологда, Россия
* E-mail: ctod28@yandex.ru
Поступила в редакцию 11.05.2021
После доработки 02.08.2021
Принята к публикации 06.08.2021
- EDN: OPUURC
- DOI: 10.31857/S0002331021040130
Аннотация
Удары молнии вызывают в воздушной линии (ВЛ) волны перенапряжений опасные для электрооборудования электрических подстанций. Импульсная корона проводов ВЛ приводит к затуханию и сглаживанию волн, что облегчает выбор средств защиты от перенапряжений. Расчеты волновых процессов обычно проводятся в программе ATP-EMTP. Проблема в том, что подключение динамической емкости короны в типовые схемы ВЛ приводит к нарушению устойчивости численного решения по формуле трапеций. Исследование показало, что методы демпфирования численных осцилляций, рекомендуемые ATP-EMTP для статических элементов, неэффективны для динамической емкости. В данной работе ВЛ моделируются цепными схемами с сосредоточенными параметрами. При большом числе звеньев они позволяют учесть распределенный характер параметров линии, включая импульсную корону, и моделировать волновые процессы с достаточной точностью. Статические элементы моделируются по формуле трапеций, динамическая емкость короны – по неявной формуле Эйлера, что обеспечивает устойчивое решение с высоким быстродействием. Эффективность предлагаемого подхода подтверждена сравнением результатов расчета с экспериментальными данными (Гари, Вагнера, Потужного) реальных ВЛ. Расчет выполнен с тремя моделями импульсной короны (ЛПИ, ВНИИЭ, Гари). Установлено: все модели короны адекватны, модель ВНИИЭ наиболее точна, модель Гари “проигрывает” ей при положительных импульсах. Модель ЛПИ, не учитывающая скачок динамической емкости в момент возникновения короны, наименее точная.
1. ВВЕДЕНИЕ
Удары молнии в воздушных линиях (ВЛ) вызывают волны перенапряжений, распространение которых представляет опасность для электрооборудования электрических подстанций. Импульсная корона проводов ВЛ приводит к затуханию и сглаживанию волн [1–4], что облегчает выбор средств защиты от перенапряжений.
К настоящему времени разработано множество моделей импульсной короны. В большинстве исследований импульсная корона моделируется одним элементом – динамической емкостью, нелинейно зависящей от напряжения. Среди наиболее распространенных моделей выделим модель ЛПИ [5], модель ВНИИЭ [6] и модель Гари [7]. Нам неизвестны работы сравнительного характера, которые позволили бы выбрать наиболее адекватную модель. В данной работе проблему выбора будем решать путем сравнения результатов расчета волновых процессов (при использовании разных моделей импульсной короны) с результатами измерений на реальных ВЛ [1–3].
Наиболее часто расчеты волновых процессов ВЛ и ПС производятся в программе ATP-EMTP. Модель импульсной короны здесь не реализована, но пользователь может ее создать как нелинейный компонент [8]. Здесь две проблемы. Для адекватного моделирования импульсной короны линия должна дробится на элементы длиной 10–30 м [8], поэтому модель ВЛ становится громоздкой, а набирать ее надо вручную. Вторая проблема серьезнее, поскольку связана с устойчивостью расчетов.
Интегрирование дифференциальных уравнений в EMTP производится в шаговых алгоритмах по формуле трапеций, которая является А-устойчивой, но не является L-устойчивой, что в жестких задачах приводит к численным осцилляциям [9]. Скачкообразное включение/изменение/отключение динамической емкости также является источником численных осцилляций, приводящих к нарушению устойчивости. Можно было бы применить известные методы демпфирования численных осцилляций формулы трапеций [10], но они эффективны только для статических элементов.
Необходимость дробления ВЛ на элементы малой длины для адекватного моделирования импульсной короны позволяет рассматривать цепные схемы с сосредоточенными параметрами в качестве альтернативной модели длинной линии. Главным достоинством цепных моделей является универсальность – они применимы для произвольных 3D систем проводников в воздухе и земле. Цепные схемы с успехом используются в теории заземлителей, что позволяет использовать разработанные модели, методы, программы [11].
Проблема численных осцилляций и нарушения устойчивости расчета волновых процессов ВЛ с импульсной короной решена применением L-устойчивой формулы Влаха третьего порядка вместо формулы трапеций [12]. Недостаток этого подхода – в значительном увеличении трудоемкости. В данной работе моделирование статических элементов производится по формуле трапеций, а моделирование динамической емкости производится по неявной формуле Эйлера, что обеспечивает устойчивое решение с высокой производительностью.
Показать эффективность предлагаемого подхода моделирования волновых процессов ВЛ с импульсной короной в цепных схемах, а также выбрать наиболее адекватную модель динамической емкости при сравнении с измерениями на реальных ВЛ [1–3] – цель настоящей работы.
2. ЦЕПНАЯ МОДЕЛЬ ТОНКОГО ПРОВОДНИКА
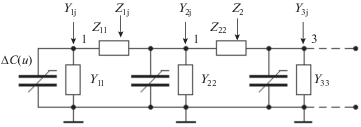
Проводники (заземляющие стержни, провода ВЛ, шины ПС) дробятся на элементы длиной l < λ/10, где λ – длина электромагнитной волны. Каждому элементу ставится в соответствие П-схема с продольным сопротивлением Z, включающим внутреннее и внешнее индуктивное сопротивление проводника, и поперечной проводимостью Y, моделирующей растекание тока в земле или емкостные токи проводников в воздухе (рис. 1). Взаимные электромагнитные связи между П-схемами учитываются взаимными сопротивлениями и проводимостями. Параметры цепной модели проводника (рис. 1) приведены в [11].
Для моделирования импульсной короны в поперечные ветви включается нелинейная емкость
где C0 – геометрическая емкость провода; Cd(u) – динамическая емкость импульсной короны.3. ДИНАМИЧЕСКАЯ ЕМКОСТЬ ИМПУЛЬСНОЙ КОРОНЫ
Коронный разряд на проводах ВЛ возникает, когда напряженность электрического поля провода превысит критическую напряженность [12]
До возникновения коронного разряда емкостной ток пропорционален статической (геометрической) емкости провода
При коронном разряде заряд провода (включая объемный заряд короны) нелинейно зависит от напряжения, тогда
Таким образом, форма записи стекающего тока провода (и уравнений длинной линии) не изменятся при коронном разряде, если геометрическую емкость провода заменить динамической емкостью
Расчетная модель динамической емкости [13, стр. 237]
Примем, что чехол короны представляет цилиндрический проводник радиуса r. Среднюю напряженность чехла E считаем постоянной величиной: E = E+ = 9 кВ/см, E = E–= 21 кВ/см [13]. В современных исследованиях E+ = 5 кВ/см, E– = 18 кВ/см [14].
Тогда
Динамическая емкость провода (с учетом E = const)
(1)
${{C}_{d}} = \frac{{dq}}{{du}} = \frac{d}{d}\frac{{2\pi \varepsilon Er}}{{Er\ln ({{2h} \mathord{\left/ {\vphantom {{2h} r}} \right. \kern-0em} r})}} = \frac{{\frac{d}{{dr}}2\pi \varepsilon Er}}{{\frac{d}{{dr}}Er\ln ({{2h} \mathord{\left/ {\vphantom {{2h} r}} \right. \kern-0em} r})}} = \frac{{2\pi \varepsilon }}{{\ln ({{2h} \mathord{\left/ {\vphantom {{2h} r}} \right. \kern-0em} r}) - 1}} = {{C}_{0}}\frac{{\ln ({{2h} \mathord{\left/ {\vphantom {{2h} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}})}}{{\ln ({{2h} \mathord{\left/ {\vphantom {{2h} r}} \right. \kern-0em} r}) - 1}},$Для дальнейшего исследования важно, что в момент возникновения коронного разряда (при r = r0) динамическая емкость согласно (1) возрастает скачком.
Модель импульсной короны ЛПИ [5]
Динамическая емкость провода
(2)
${{C}_{d}}(u) = {{C}_{0}} + {{C}_{0}} \times {5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}k{{\left( {{u \mathord{\left/ {\vphantom {u {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}} - 1} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}},\,\,\,\,{{k}_{ - }} = 0.375,\,\,\,\,{{k}_{ + }} = 0.78,$Модель импульсной короны ВНИИЭ [6]
(3)
${{C}_{d}}(u) = {4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}{{C}_{0}}B\sqrt[3]{{{u \mathord{\left/ {\vphantom {u {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}}},\,\,\,\,{{B}_{ + }} = 1.02,\,\,\,\,{{B}_{ - }} = 0.85.$В момент возникновения коронного разряда, при u = U0, емкость короны возрастает скачком, что согласуется с (1).
Модель импульсной короны Гари [6]
где d – диаметр провода. В момент возникновения коронного разряда динамическая емкость возрастает скачком, что согласуется с (1) и (3). В данной модели динамическая емкость зависит от диаметра провода.3. РАСЧЕТ ИМПУЛЬСНЫХ ПРОЦЕССОВ МЕТОДОМ ДИСКРЕТНЫХ СХЕМ
Расчет цепной схемы с нелинейной емкостью (рис. 1) производится во временной области методом дискретных схем. Этот метод используется и в EMTP.
Временной интервал разбивается на n равных шагов длиной h. При малом шаге произвольные частотно-зависимые сопротивления и проводимости моделируются дискретными резистивными схемами.
Найдем дискретную схему емкости. Выполним интегрирование дифференциального уравнения, связывающего напряжение и ток, на k–м временном шаге по формуле трапеций
(5)
$i = C\frac{{du}}{{dt}} \Rightarrow \frac{{{{i}_{{k + 1}}} + {{i}_{k}}}}{2} = C\frac{{{{u}_{{k + 1}}} - {{u}_{k}}}}{h} \Rightarrow {{i}_{{k + 1}}} = \frac{{2C}}{h}{{u}_{{k + 1}}} - \left( {{{i}_{k}} + \frac{{2C}}{h}{{u}_{k}}} \right) = G{{u}_{{k + 1}}} - {{J}_{k}},$(6)
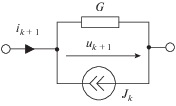
$i = C\frac{{du}}{{dt}} \Rightarrow {{i}_{{k + 1}}} = C\frac{{{{u}_{{k + 1}}} - {{u}_{k}}}}{h} = \frac{C}{h}{{u}_{{k + 1}}} - \frac{C}{h}{{u}_{k}} = G{{u}_{{k + 1}}} - {{J}_{k}}.$Уравнениям (5), (6) соответствует дискретная схема (рис. 2)
Дискретная схема индуктивности получается аналогично. Дискретные схемы произвольного частотно-зависимого сопротивления и проводимости получены в [11].
Таким образом, расчет переходного процесса в цепных схемах (рис. 1) сводится к расчету резистивной цепи на последовательности временных шагов. Использование формулы трапеций, имеющей второй порядок точности, обеспечивает высокую точность расчетов.
Проблема в том, что формула трапеций не является L-устойчивой [9]. При определенных условиях она приводит к численным осцилляциям, что можно показать на примере.
Пусть к емкости C приложено импульсное напряжение с линейным фронтом длительностью T и единичной амплитудой. Примем шаг h = T, тогда напряжение шагов u0 = 0, u1 = u2 = ..un = 1.
Найдем ток емкости по формуле трапеций (5) при C/h = 1
Таким образом, ток осциллирующий i = (0, 2, –2, 2, –2…), при численных расчетах такое решение разваливается.
С использованием неявной формулы Эйлера (6) при C/h =1
Таким образом, i = (0, 1, 0, 0…), т.е. численных осцилляций нет, конденсатор заряжается за один шаг и далее не пропускает ток, что соответствует физике процесса.
Рассмотренная проблема возникает при моделировании коронного разряда. При скачкообразном изменении динамической емкости формула трапеций приводит к численной осцилляции и неустойчивости решения.
Рассмотрим возможные способы решения проблемы.
В работе [16] для решения жестких задач рекомендовано использование неявной формулы Эйлера, которая является L-устойчивой. Выполненные расчеты подтверждают обоснованность данной рекомендации, однако этот способ потребует значительно уменьшить шаг интегрирования (по сравнению с формулой трапеций) для достижения заданной точности решения. Автоматическое изменение шага, рекомендованное в [16], здесь нецелесообразно (из-за высокой трудоемкости в сложных цепях), поскольку потребует пересчета матрицы узловых проводимостей на каждом шаге.
В работе [10] для решения жестких задач рекомендуется применение линейной комбинации формулы трапеций и неявной формулы Эйлера в соотношении 0.85/0.15. Этот способ реализован в программе EMTP. Исследование этого способа показало, что он эффективен для моделирования статических емкостей, но не гарантирует устойчивое решение при моделировании динамической емкости – доля неявной формулы Эйлера должна быть значительно увеличена.
В работе [17] используется формула трапеций, однако, если происходит топологическое изменение цепи, “включается” неявная формула Эйлера с вдвое меньшим шагом, что позволяет не пересчитывать матрицу узловых проводимостей цепи, найденную по формуле трапеций. Этот способ эффективен при подключении единичного элемента, однако подключение динамической емкости производится практически во всех узлах провода ВЛ со смещением во времени по мере распространения волны, а значит формула трапеций фактически заменяется неявной формулой Эйлера, а число шагов удваивается.
В работе [12] устойчивое решение задачи получено с использование L-устойчивой формулы Влаха 3 порядка, однако, трудоемкость решения и требования к оперативной памяти возрастают в несколько раз по сравнению с формулой трапеций из-за расчетов с комплексными числами.
Простое, устойчивое и достаточно точное решение дает следующая методика: формула трапеций используется для моделирования индуктивностей и емкостей с постоянными параметрами, для моделирования переменной части динамической емкости ΔC = Cd – C0 используется неявная формула Эйлера.
4. ОСОБЕННОСТИ МОДАЛЬНОГО МЕТОДА РАСЧЕТА ВОЛНОВЫХ ПРОЦЕССОВ ВЛ С ИМПУЛЬСНОЙ КОРОНОЙ
Волновые процессы в многопроводных ВЛ рассчитываются модальным методом, который исследован в работе [4] и других работах этих авторов. Идея метода заключается в преобразованиях уравнений n-проводной длинной линии к системе из n-уравнений однопроводных, независимых друг от друга линий, иначе, из общего волнового процесса выделяются независимые модальные (волновые) каналы.
Пример. В крайний провод трехпроводной ВЛ (с горизонтальным расположением проводов) вводится импульс тока 1 А, два другие провода изолированы. Вектор фазных токов I = (1,0,0)T. Применение модального метода приводит к матрице токов волновых каналов (с округлением результатов для наглядности)
Первый столбец определяет волновой канал “провода–земля”, поскольку токи всех проводов, равные 1/3 А, движутся в прямом направлении по проводам и возвращаются через землю. Затухание и деформация волны земляного канала определяется сопротивлением земли (по формуле Карсона), методика расчета которого с помощью эквивалентных схем рассмотрена в [4], в шаговых алгоритмах – в [12].
Второй столбец определяет волновой канал “крайний провод–крайний провод”, третий столбец – “крайние провода–средний провод”. Токи этих каналов замыкаются по проводам (без возврата через землю), что соответствует распространению волны в воздухе, т.е. с очень малым затуханием и запаздыванием (из-за потерь в проводах), которыми в рассматриваемых далее задачах (при пробеге волн до 10 км) можно пренебречь. Это позволяет объединить волновые каналы в воздухе (независимо от числа проводов), что упрощает расчеты. В результате рассматриваем волновой канал в земле Igr и волновой канал в воздухе Iair, где
Модальный метод, основанный на принципе наложения, применим только в линейных задачах. В работе [4] и других работах этих авторов показано, что для применения модального метода в нелинейных распределенных системах характеристика динамической емкости должна быть аппроксимирована кусочно-постоянной функцией, т.е. задача становится линейной на каждом временном шаге. В дискретные моменты времени в дискретные узлы схемы подключается сосредоточенная емкость, величина которой определяется напряжением в данный момент времени.
Этот подход реализован и в данной работе. Нелинейная емкость (2)–(4) принимается постоянной величиной в пределах каждого шага, т.е. нелинейная характеристика динамической емкости становится кусочно-постоянной функцией во времени. На каждом шаге проводится последовательный расчет всех волновых каналов, полученные напряжения и токи волновых каналов суммируются, в конце шага определяется новое значение динамической емкости, которое используется на следующем шаге. Этот подход далее успешно протестирован в сравнении с экспериментальными данными.
5. СРАВНЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТА С ИЗМЕРЕНИЯМИ НА РЕАЛЬНЫХ ВЛ
Расчеты волновых процессов ВЛ выполнены в программе ZYM [11].
Задача 1. В экспериментах Гари (C. Gary) [1] в начало крайнего провода ВЛ (рис. 3) вводится импульс положительного напряжения
Рис. 3.
Напряжение на расстоянии 0, 1, 3, 7, 10 км от начала ВЛ: 1 – измерения Гари (из документации к программе EMTP-RV); 2 – расчет с моделью короны ВНИИЭ (3).
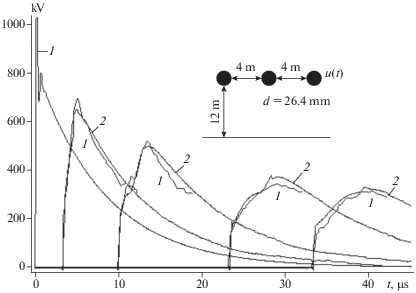
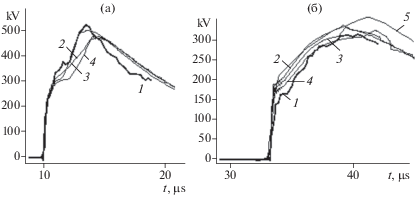
Расчеты хорошо согласуются с данными измерений (рис. 3). По результатам расчета на расстоянии 3 км (рис. 4a) и 10 км (рис. 4б) видим, что модель ВНИИЭ наиболее точная, модель Гари (из-за результата на 3 км) и модель ЛПИ менее точны. Заметим, что наши расчеты (по всем моделям короны) лучше согласуются с экспериментом, чем расчеты по программе EMTP-RV (рис. 4б).
Рис. 4.
Напряжение на расстоянии 3 км (a), 10 км (б) от начала ВЛ: 1 – измерения Гари; 2 – расчет с моделью короны ЛПИ (2); 3 – расчет с моделью короны ВНИИЭ (3); 4 – расчет с моделью короны Гари (4); 5 – расчет по программе EMTP-RV (из документации к этой программе).
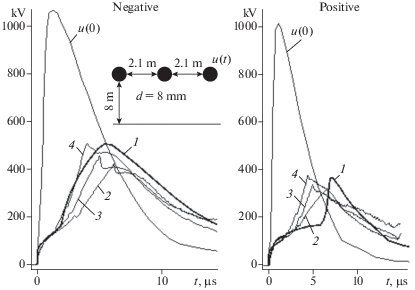
Задача 2. В экспериментах Вагнера (Wagner C.F.) [2] в начало крайнего провода трехпроводной ВЛ вводятся различные по амплитуде и полярности импульсы напряжения (рис. 5). Грунт низкоомный (ρ = 50 Ом · м), поэтому влиянием заземленных тросов, которые включены параллельно сопротивлению грунта, при расчетах можно пренебречь. Сравним напряжение, измеренное на расстоянии 2222 м, с результатами расчетов (рис. 5). Модель ВНИИЭ и модель Гари одинаково точны при отрицательной полярности, но модель ВНИИЭ точнее при положительной полярности. Модель ЛПИ здесь наименее точная, динамическая емкость при малых напряжениях недостаточна, при больших напряжениях избыточна. Были рассмотрены и другие варианты [2], которые приводят к аналогичным выводам.
Рис. 5.
Напряжение в начале линии u(0) и на расстоянии 2222 м (7290’ в оригинале) при отрицательной и положительной полярности: 1 – измерения Вагнера; 2 – расчет с моделью короны ЛПИ (2); 3 – расчет с моделью короны ВНИИЭ (3); 4 – расчет с моделью короны Гари (4); удельное сопротивление грунта ρ = 50 Ом · м.
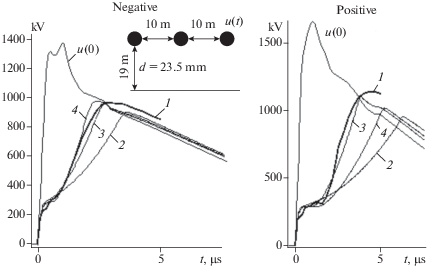
Задача 3. В экспериментах Потужного и Фертика [3] в начало крайнего провода ВЛ вводятся импульсы напряжения разной полярности и амплитуды (рис. 6). Сравним результаты измерений и расчетов на расстоянии 5.52 км (рис. 6). При отрицательной полярности импульса наилучшее совпадение с измерениями дают расчеты с моделью Гари, но расчеты с моделью ВНИИЭ также хорошо согласуются с измерениями. Расчеты с моделью ЛПИ наименее точные. При положительной полярности импульса расчеты при всех моделях короны хорошо описывают затухание волны, но не позволяют моделировать запаздывание фронта волны с достаточной точностью (рис. 6), поэтому здесь сравнение моделей затруднительно.
Рис. 6.
Напряжение в начале линии u(0) и на расстоянии 5.52 км: 1 – измерения Потужного и Фертика; 2 – расчет с моделью короны ЛПИ (2); 3 – расчет с моделью короны ВНИИЭ (3); 4 – расчет с моделью короны Гари (4); удельное сопротивление грунта ρ = 200 Ом · м.
Подводя итоги решенных задач, считаем модель импульсной короны ВНИИЭ (3) наиболее адекватной для ВЛ с одиночными проводами.
ВЫВОДЫ
Моделирование грозовых перенапряжений ВЛ с импульсной короной требует дробления проводов на элементы малой длины (10–30 м) так, что цепные модели с сосредоточенными параметрами конкурентоспособны по сравнению с моделью длинной линии.
Расчеты волновых процессов в реальных ВЛ с использованием трех наиболее распространенных моделей короны при сравнении с экспериментальными данными показали, что модель ВНИИЭ (3) является наиболее адекватной. Более сложная модель Гари (4) дает избыточную динамическую емкость при положительной полярности. Модель ЛПИ (2) не учитывает эффект скачка динамической емкости при возникновении короны, из-за чего динамическая емкость занижена при малых напряжениях короны, и поэтому не возникает характерной “ступеньки” в графике волны напряжения. При больших напряжениях динамическая емкость в модели ЛПИ завышена по сравнению с моделью ВНИИЭ.
Скачкообразное изменение динамической емкости является источником численных осцилляций и нарушения устойчивости расчета волновых процессов по формуле трапеций в программах типа EMTP. Рекомендуется выделять переменную составляющую динамической емкости ΔC = Cd – C0 и моделировать ее по неявной формуле Эйлера, что обеспечивает устойчивое решение при достаточной точности расчетов.
Список литературы
Gary C., Timotin A., Cristescu D. Prediction of surge propagation influenced by corona and skin effect. IEE Proc. 1983. V. 130. Pt. A. № 5. P. 264–272.
Wagner C.F., Gross I.W., Lloyd B.L. High-Voltage Impulse Tests on Transmission Lines. Transactions of the American Institute of Electrical Engineers. Part III: Power Apparatus and Systems. 1954. V. 73. Issue 2. P. 196–209.
Потужный А.К., Фертик С.М. Затухание волн высокого напряжения в 35-kV линии // Электричество. 1938. № 1. С. 29–39.
Ефимов Б.В., Гумерова Н.И. Моделирование деформации грозовых волн в воздушных линиях с учетом совместного влияния конструкции опор, короны на проводах и потерь в земле // Труды КНЦ РАН. Энергетика. 2013. Вып. 7(17). С. 13–32.
Богатенков Н.М., Гумерова Н.И., Костенко М.В. и др. Вольт-кулоновые характеристики короны на расщепленных проводах при импульсном напряжении // Труды ЛПИ. Электроэнергетика. № 340. 1974. С. 8–13.
Бочковский Б.Б. Импульсная корона на одиночных и расщепленных проводах // Электричество. 1966. № 7. С. 22–27.
Gary C., Dragan G., Langu I. Impulse corona discharge energy around the conductors. IEEE Industry Applications Society Annual Meeting, Oct 1990. P. 922–924.
Anane Z., Bayadi A., Huang K. Distortion Phenomena on Transmission Lines Using Corona Modeling ATP/EMTP. IEEE Transactions on Dielectrics and Electrical Insulation. 2018. V. 25. № 2. P. 383–389.
Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999. 685 с.
Alvarado F.L., Lasseter R.H, Sanchez J.J. Testing of trapezoidal integration with damping for the solution of power transient problems. IEEE Trans. on Power Apparatus and Systems. 1983. V. PAS-102. № 12. P. 3783–3790.
Шишигин С.Л., Шишигин Д.С. Расчет заземлителей (монография). Вологда: ВоГУ, 2020. 219 с.
Шишигин С.Л., Шишигин Д.С., Смирнов И.Н. Расчет грозовых перенапряжений воздушных линий в цепных схемах с учетом частотных свойств грунта // Материаловедение. Энергетика. 2020. Т. 26. № 4. С. 87–99.
Техника высоких напряжений / Под ред. Разевига Д.В., Изд. 2-е, перераб. и доп. М., “Энергия”, 1976. 488 с.
Sun Y., Montenegro A., Tobin T. Corona characteristics of aerial conductors under switching impulse voltages. IEEE Transactions on Dielectrics and Electrical Insulation. 2020, V. 27. Issue: 1. P. 206–213.
Демирчян К.С. Теоретические основы электротехники. Учебник для вузов. 5-е изд. Т. 2. / Демирчян К.С., Нейман Л.Р., Коровкин Н.В. СПб.: Питер, 2009. 432 с.
Демирчян К.С., Бутырин П.А. Моделирование и машинный расчет электрических цепей. М.: Высш. школа, 1988. 335 с.
Marti J.R., Lin J. Suppression of numerical oscillations in the EMTP. IEEE Trans. on Power Systems. 1989. V. 4. № 2. P. 739–747.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Энергетика