Известия РАН. Энергетика, 2022, № 2, стр. 44-50

Определение взаимной индуктивности коаксиальных соленоидов имеет важное практическое значение и используется во многих практических приложениях, одно из которых характеризуется термином “Coilgun” [1, 2] как разновидности электромагнитного ускорителя соленоидов в управляемом магнитном поле, что, в свою очередь, обуславливает необходимость в оценках взаимных индуктивностей соленоидов и возникающих сил при протекании токов. Эти вопросы находятся в поле зрения специалистов, занимающихся проблемами электромагнитного ускорения уже достаточно давно, и в качестве примера можно привести работу [3], опубликованную в 1961 г.

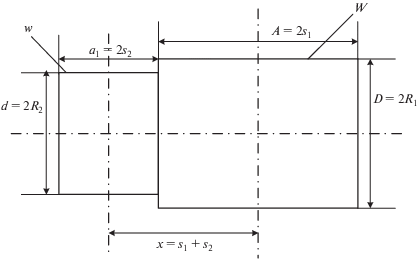
В работе [2] построены графические зависимости для взаимной индуктивности коаксиальных соленоидов в функции расстояния между плоскостями симметрии x (рис. 1).

На рис. 1 показан характерный случай расположения соленоидов с примыкающими торцами и с геометрией, определенной подрисуночной подписью к рис. 1. В работе [4] были даны выражения для электродинамических сил, действующих на соосный контур с током в поле соленоида при его перемещении вдоль оси, в которой были указаны предпосылки для реализации возвратно-поступательного движения контура за счет изменения направления тока при прохождении нулевой плоскости, а затем на достаточном удалении от торцевых плоскостей. Вопросы определения взаимной индуктивности в коаксиальных соленоидах рассматривались ранее в работах [4, 5].

На этой основе в работах [5–7] рассматривались также и электродинамические силы при протекании токов, поэтому целесообразность сопоставления методов определения взаимных индуктивностей не вызывает сомнений.

Для определения взаимной индуктивности $M$ в [2] при $x = \operatorname{var} $ приведено выражение:

где ${{l}_{1}} = x - {{R}_{1}},$ ${{l}_{2}} = x + {{R}_{1}},$ ${{d}_{1}} = \sqrt {{{{\left( {x - {{R}_{1}}} \right)}}^{2}} + R_{1}^{2}} ,$ ${{d}_{2}} = \sqrt {{{{\left( {x + {{R}_{1}}} \right)}}^{2}} + R_{1}^{2}} ,$ в которую подставляются данные из подрисуночной подписи. Тогда при $x = 0.024$ м, ${{R}_{1}} = 0.02$ м и ${{R}_{2}} = 0.016$ м будем иметь: ${{l}_{1}} = 0.004$ м, ${{l}_{2}} = 0.044$ м, ${{d}_{1}} = 0.0204$ м и ${{d}_{2}} = 0.0483$ м, и величина $M$ оказывается равной:

Результат вычисления приводит к значению $0.673 \times {{10}^{{ - 6}}}$ Гн вместо $0.2 \times {{10}^{{ - 6}}}$ Гн, вытекающего из анализа кривой для $M$ (Fig. 4 в [2]). Поэтому есть необходимость в сопоставлении взаимной индуктивности по имеющимся альтернативным методикам и расчетам. Оценку взаимной индуктивности в этом конкретном случае будет производить по методике, данной в [6], и по расчетным выражениям, данным в [5].

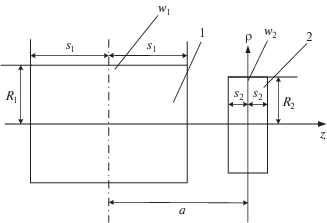
По методике, изложенной в [6], взаимная индуктивность коаксиальных соленоидов с примыкающими торцами с внешней стороны в соответствии с рис. 2 определяется по формулам:

где

${{x}_{1}} = x + \frac{{A + a}}{2},$ ${{x}_{2}} = x - \frac{{A - a}}{2},$ ${{x}_{3}} = x + \frac{{A - a}}{2},$ ${{x}_{4}} = x - \frac{{A + a}}{2},$ а ${{F}_{1}} - {{F}_{4}}$ – значение функций $F,$ заданных таблично при $\delta = \frac{d}{D}$ и отношениях $\lambda _{1}^{2} = {{\left( {\frac{D}{{2{{l}_{1}}}}} \right)}^{2}},$ $\lambda _{2}^{2} = {{\left( {\frac{D}{{2{{l}_{2}}}}} \right)}^{2}},$ $\lambda _{3}^{2} = {{\left( {\frac{D}{{2{{l}_{3}}}}} \right)}^{2}},$ $\lambda _{4}^{2} = {{\left( {\frac{D}{{2{{l}_{4}}}}} \right)}^{2}}.$

В данном конкретном случае ${{x}_{1}} = 0.048$ м, ${{x}_{2}} = 0.008$ м, ${{x}_{3}} = 0.004$ м, ${{x}_{4}} = 0$ и соответственно ${{l}_{1}} = 0.052$ м, ${{l}_{2}} = 0.0215$ м, ${{l}_{3}} = 0.0447$ м, ${{l}_{4}} = 0.02$ м, $\delta = \frac{{0.032}}{{0.04}} = 0.8,$ $\lambda _{1}^{2} = {{\left( {\frac{{0.02}}{{0.052}}} \right)}^{2}} \cong 0.148,$ $\lambda _{2}^{2} = {{\left( {\frac{{0.02}}{{0.0215}}} \right)}^{2}} \cong 0.865,$ $\lambda _{3}^{2} = {{\left( {\frac{{0.02}}{{0.0447}}} \right)}^{2}} \cong 0.2,$ $\lambda _{4}^{2} = {{\left( {\frac{{0.02}}{{0.02}}} \right)}^{2}} = 1.0.$

Для нахождения значений $F1,F2,F3,F4$ следует воспользоваться таблицей 7.1 в [6], по которой будем иметь для ${{F}_{1}} - {{F}_{4}}$ следующие численные значения: 0.998, 0.938, 0.997, 0.912. Подстановкой значений в формулу (3) с учетом произведения числа витков, принятых равных 24, и геометрических размеров $d = 2{{R}_{2}},$ $a = 2{{s}_{2}},$ и $A = 2{{s}_{1}},$ а именно, $d = 0.032$ м, $a = 0.008$ м и $A = 0.04$ м найдем:

т.е. значение весьма близкое к графику $M$ от $x$ при $x = 0.024$ м в [2].

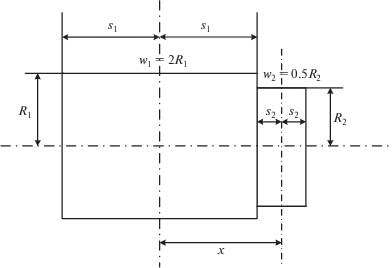
Положение коаксиального соленоида с индексом 2 относительно правого или левого торца соленоида с индексом 1 (рис. 1, 2) значения не имеет. Альтернативой для этой методики расчета можем служить комплекс расчетных выражений, данных в [5], для общего случая расположения коаксиальных соленоидов, показанных на рис. 3.

В [5] выражение для взаимной индуктивности представлено в виде рядов:

где (рис. 3)

и геометрические размеры записаны в соответствии рис. 3, ${{w}_{1}},{{w}_{2}}$ – число витков соленоидов 1 и 2.

Зададимся теперь значением $a$ равным $x$ (рис. 1), т.е. $a = 0.024,$ ${{s}_{1}} = {{R}_{1}},$ ${{w}_{1}}{{w}_{2}} = 24,$ ${{R}_{2}} = 0.016$ м, ${{s}_{2}} = 0.004$ м и ${{s}_{1}} = 0.02$ м, и найдем, что ${{q}_{1}} = 0,$ ${{q}_{2}} = 2.5,$ ${{q}_{3}} = 3.0$ и ${{q}_{4}} = 0.5.$

Перед суммой в (4) имеем $\pi \times 4\pi \times 24 \times 0.02{\text{/}}2 \times 0.5 \cong 1.895 \times {{10}^{{ - 6}}}$ Гн. Для ${{q}_{1}} = 0$ получаем под знаком суммы в (4) 0.374, для ${{q}_{2}} = 2.5$ – (–0.0917), для ${{q}_{3}} = 3.0$ имеем 0.0783, и для ${{q}_{4}} = 0.5$ – (–0.2428). Объединяя эти значения и умножая их на величину, стоящую перед суммой в (4), получаем $0.223 \times {{10}^{{ - 6}}}$ Гн. Таким образом результаты расчетов по методикам, данным в [5] и [6], дают близкие численные результаты, которые и служат основанием для ревизии выражения (2), приведенного в [4]. Этому выражению здесь приписан номер 1.

Близость численных значений позволяет рекомендовать для определения электродинамических сил следующее выражение, данное в [5] (рис. 3):

где ${{q}_{k}}$ определены в соответствии с (5).

Тогда имеем в конфигурации, принятой для рис. 1 и рис. 3, где $a = x = 0.024$ м, ${{s}_{2}} = 0.004$ м, ${{s}_{1}} = {{R}_{1}} = 0.02$ м, ${{R}_{2}} = 0.016$ м с числом витков 24 и 1, следующее выражение перед суммой:

Вычисления под знаком суммы в (6) с подстановкой ${{q}_{1}} - {{q}_{4}}$ приводят к следующим численным значениям при ограничении первыми тремя членами ряда (6): для ${{q}_{1}} = 0$ имеем (+0.5), для ${{q}_{2}} = 2.5$ (–0.02989), соответственно для ${{q}_{3}} = 3.0$ (+0.02318) и для ${{q}_{4}} = 0.5$ (–0.1576). В сумме получаем значение, равное 0.3357. Тогда для силы взаимодействия находим: $f = 118.435 \times {{10}^{{ - 6}}}{{i}_{1}}{{i}_{2}}0.3357$ = $39.757 \times {{10}^{{ - 6}}}{{i}_{1}}{{i}_{2}},$ а для оценки силы взаимодействия при синусоидальном процессе и действующих значениях токов ${{10}^{4}}$ А будем иметь в среднем во времени: $F = 39.757 \times {{10}^{2}}$ Ньютон или $405.52$ кГс.

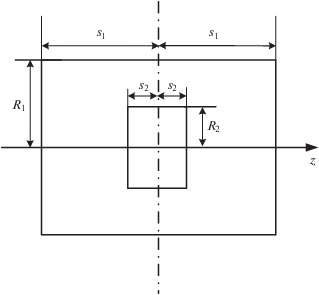
Вернемся к вопросу о взаимной индуктивности для случая симметричного расположения коаксиальных соленоидов, когда соленоид меньшего радиуса располагается целиком внутри другого с торцами, равноудаленными от торцов внешнего соленоида, как показано на рис. 4.

В этом случае взаимная индуктивность определяется выражением:

где

Подставляя численные значения, соответствующие указанным в подрисуночной надписи на рис. 1, т.е., принимая произведения витков равным 24, ${{s}_{1}} = {{R}_{1}} = 0.02$ м, ${{R}_{2}} = 0.8{{R}_{1}} = 0.016$ м, ${{s}_{2}} = 0.25{{R}_{2}} = 0.004$ м, и, следовательно, ${{q}_{1}} = - 1.2$ и ${{q}_{2}} = - 0.8,$ будем иметь:

Оценка первой квадратной скобки выражаются численным значением 1.5424, а для второй квадратной – оценка значением (–1.2637). Поэтому максимальное значение индуктивности в конфигурации рис. 4 равно:

которое совпадает практически с численным значением, определяемым по кривой Fig. 4 работы [2] при $x = 0.$

Естественно предположить, что максимальное значение для взаимной индуктивности должно вытекать и из выражения (1) в случае его правомерности при значении $х = 0.$ Тогда ${{l}_{1}} = - {{R}_{1}},$ ${{l}_{2}} = {{R}_{1}},$ ${{d}_{1}} = \sqrt 2 {{R}_{1}},$ ${{d}_{2}} = \sqrt 2 {{R}_{1}},$ ${{R}_{1}} = 0.02$ м и ${{R}_{2}} = 0.016$ м. Для квадратной скобки в (1) имеем: численное значение 7460, а для взаимной индуктивности $0.00121 \times {{10}^{{ - 7}}} \times 7460$ $ \cong $ $0.903 \times {{10}^{{ - 6}}}\,\,{\text{Гн}}{\text{.}}$

Из вышеизложенного следует необходимость корректировки выражения (1), данного в [2], и целесообразность использования методики, данной в [6], выражения (4) с учетом (5) для определения взаимной индуктивности, а также выражения (6) при определении электродинамических сил для внешнего расположения соленоидов. Для внутреннего расположения соленоидов рекомендации по расчету сил даны в [5], а управление движением можно осуществить изменением величины и направления токов.

Заметим в заключении, что реализация ускоренного перемещения “coilgun” хорошо проиллюстрировано в работе [8], где ускорение проводящего объекта осуществляется в многосекционном индукторе, одна половина которого подключена к условно положительному генератору, а вторая – к отрицательному, и на всем протяжении объект испытывает ускоряющее воздействие только одного знака.