Известия РАН. Энергетика, 2022, № 2, стр. 51-72

ВВЕДЕНИЕ

Одной из классических проблем теории нестационарной теплопроводности является задача исследования температурного режима твердых тел в условиях конвективного теплообмена с окружающей средой. В известных монографиях Лыкова [1] и Карташова [2] выполнен детальный обзор указанной проблемы, а также приведены аналитические методы решения при постоянном коэффициенте теплоотдачи $\left( {\alpha = {\text{const}}} \right).$ В ряде приложений как температурная функция (ТФ)¹¹, так и тепловой поток на границе раздела твердого тела и обтекающего его потока жидкости зависят от времени. Поэтому в общем случае функцией времени будет также связывающая их величина $\alpha = \alpha \left( t \right).$ В ряде важных приложений (пузырьковое кипение, капельная конденсация, снарядный режим течения двухфазного потока, развитие гидродинамической неустойчивости) изменения теплогидравлических параметров носят периодический, квазипериодический или стохастический характер. Следовательно, аналогичные колебания должен испытывать также характеризующий эти процессы коэффициент теплоотдачи.

Как показано в обзоре [3], построение точного аналитического решения краевой задачи для уравнения теплопроводности с нестационарным граничным условием (ГУ) третьего рода наталкивается на принципиальные затруднения. Их причина заключается в невозможности согласования ГУ с классическим методом разделения переменных Фурье, являющимся основой большинства методов решения дифференциальных уравнений математической физики. Процедура решения спектральной задачи для произвольной функции $\alpha \left( t \right)$ приводит к собственным значениям и собственным функциям, зависящим от времени. Это не позволяет представить решение задачи для линейного уравнения теплопроводности в виде интеграла или ряда Фурье–Ханкеля для области канонического типа [4]. Отсюда следует, что метод разделения переменных позволяет записать зависимость ТФ от времени и координат не в замкнутом виде, а в квадратурах. Это позволяет представить формальное точное решение лишь в виде бесконечного ряда последовательных приближений.

Существенный прогресс в этой области был достигнут в недавних работах [5, 6], где решения строилось на основе пикаровского процесса последовательных приближений с использованием расщепления обобщенного интегрального преобразования Фурье. В результате в [5, 6] были получены и представлены в различных классах функций аналитические решения данной краевой задачи для четырех характерных функций $\alpha \left( t \right)$ – линейной, экспоненциальной, степенной и корневой.

ЗАКОН ТЕПЛОПРОВОДНОСТИ

В основе классической теории теплопроводности лежит закон теплопроводности Фурье (или “гипотеза Фурье”), согласно которому поток тепла $q$ пропорционален градиенту температуры²²:

Процесс распространения тепла в неподвижной среде описывается законом сохранения энергии: Использование в (2) гипотезы Фурье приводит к параболическому уравнению теплопроводности: Здесь $t$ – время; $x$ – координата, отсчитываемая от поверхности вглубь тела; $\vartheta = T - {{T}_{0}}$ – температурная функция (ТФ); ${{T}_{0}}$ – температура на бесконечности тела; ${{q}_{V}}$ – объемная плотность тепловых источников; $c$ – удельная теплоемкость; $\rho $ – плотность; $a = {\lambda \mathord{\left/ {\vphantom {\lambda {c\rho }}} \right. \kern-0em} {c\rho }}$ – коэффициент температуропроводности; $\lambda ~$ – коэффициент теплопроводности.

Закон теплопроводности Фурье описывает процесс распространения тепла потоком взаимодействующих элементарных частиц (электронов, атомов, молекул). Его характерным свойством является бесконечная скорость распространения теплового возмущения [1, 2]. Согласно (3), изменение температуры в какой-либо точке тела приводит к ее мгновенному изменению во всех других точках. Это противоречит физическим законам, ограничивающим бесконечные значения скоростей распространения сигналов. Причина указанного парадокса заключается в том, что гипотеза Фурье не учитывает молекулярно-кинетические закономерности, связанные со скоростями движения элементарных частиц, а также длиной и временем их свободного пробега. Учет конечной скорости распространения теплового возмущения становится необходимым при описании процессов с экстремальными тепловыми воздействиями и со сверхбыстрым изменением температурных полей. Для последующего изложения важно подчеркнуть, что указанные процессы практически всегда имеют импульсно-периодический характер.

В 1958 г. Каттанео (Cattaneo) [7] и Вернотте (Vernotte) [8] независимо предложили обобщение гипотезы Фурье на случай конечной скорости распространения тепла путем введения в его левую часть релаксационного члена³³:

Использование гипотезы (4) в (2) приводит к гиперболическому уравнению теплопроводности:

учитывающему запаздывание реакции неравновесной системы на термическое возмущение. Согласно (5), тепловой поток обладает инерционностью: он откликается на изменение температурного градиента не мгновенно, как в равновесной системе, а через конечное время релаксации ${{t}_{r}}.$ При ${{t}_{r}} \to 0$ гиперболическое уравнение теплопроводности (5) сводится к параболическому уравнению (3).

ПРОЦЕССЫ ТЕПЛООБМЕНА С ПЕРИОДИЧЕСКОЙ ИНТЕНСИВНОСТЬЮ

Осреднение коэффициента теплоотдачи. В монографии [9] предложен метод анализа влияния теплофизических свойств и геометрии твердого тела на осредненную интенсивность теплоотдачи. В рамках метода реальная картина теплогидравлических флуктуаций в объеме теплоносителя представлена “истинным коэффициентом теплоотдачи” (ИКТ) на поверхности теплообмена, который периодически изменяется во времени относительно своего среднего значения. Принимается, что амплитуда и период этих колебаний, а также вид функции $\alpha \left( t \right)$ отражают колебания теплогидравлических параметров в жидкости. Дальнейшее развитие метода [9] и результаты его применения к различным видам процессов теплообмена с периодической интенсивностью представлены в монографии [10] (см. приведенную библиографию). В настоящей работе предлагается обобщение подхода [9, 10] на случай гиперболической модели теплопроводности.

Рассмотрим кратко параболическую модель теплопроводности для пластины толщиной $\delta .$ Вследствие линейности уравнения (3) ТФ и тепловой поток можно представить в виде: $\vartheta $ = $\left\langle \vartheta \right\rangle + \vartheta {\kern 1pt} ',$ $q$ = $\left\langle q \right\rangle + q{\kern 1pt} '.$ Стационарная часть $ТФ$ описывается уравнением:

Ее пульсационная составляющая удовлетворяет уравнению:

ТФ и тепловой поток на поверхности теплообмена $x = \delta $ связаны ГУ третьего рода: $\alpha {{\vartheta }_{\delta }} = {{q}_{\delta }}.$ Представляя $\alpha \left( t \right)$ в виде суммы осредненной $\left\langle \alpha \right\rangle $ и пульсационной $\alpha {\kern 1pt} '\left( t \right)$ частей, перепишем это ГУ в виде:

Разделив обе части этого уравнения на $\left\langle {{{\vartheta }_{\delta }}} \right\rangle ,$ получаем:

Здесь $\tilde {\alpha } = {{\alpha {\kern 1pt} '} \mathord{\left/ {\vphantom {{\alpha {\kern 1pt} '} {\left\langle \alpha \right\rangle }}} \right. \kern-0em} {\left\langle \alpha \right\rangle }},$ $\theta = {{\vartheta _{\delta }^{'}} \mathord{\left/ {\vphantom {{\vartheta _{\delta }^{'}} {\left\langle {{{\vartheta }_{\delta }}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{\vartheta }_{\delta }}} \right\rangle }}$ – безразмерные пульсации; ${{\alpha }_{m}}$ – стандартный коэффициент теплоотдачи (СКТ).

Функция $\alpha \left( t \right)$ по определению равна частному от деления локальных величин:

Осредняя это равенство по периоду, получаем:

Величина $\left\langle \alpha \right\rangle $ представляет собой действительное (“истинное”) среднее значение коэффициента теплоотдачи. Мы будем отождествлять его с коэффициентом теплоотдачи, определяемым в теории стационарного конвективного теплообмена. Следовательно, $\left\langle \alpha \right\rangle $ по определению не зависит от теплового влияния твердого тела. Периодическая составляющая $\alpha {\kern 1pt} '$ должна отражать механизм теплогидравлических пульсаций в омывающем тело потоке жидкости.

Величина ${{\alpha }_{m}},$ полученная по процедуре “стандартного” осреднения, определяется как частное от деления осредненного теплового потока на осредненную ТФ (обе величины берутся на поверхности теплообмена):

Важно подчеркнуть, что СКТ находится по измеренным в эксперименте средним величинам, поэтому их зависимость от теплофизических характеристик тела будет отражается и на величине ${{\alpha }_{m}}.$

Фактор сопряженности. Проведем анализ взаимосвязи осредненных по различным законам коэффициентов теплоотдачи – $\left\langle \alpha \right\rangle $ и ${{\alpha }_{m}}.$ Легко убедиться, что при $\vartheta _{\delta }^{'} \ne 0$ пульсационные величины $\vartheta _{\delta }^{'},\,\,~q_{\delta }^{'}$ в правой части (7) при осреднении сохраняются. В [9, 10] был введен “фактор сопряженности” – отношение СКТ к истинному осредненному коэффициенту теплоотдачи:

Величина $\varepsilon $ может использоваться в виде поправочного множителя к стандартному (т.е. “стационарному”) коэффициенту теплоотдачи, определяемому в теории конвективного теплообмена без учета теплового сопряжения. Из (7), (8) следует, что в общем случае имеют место неравенства:

Таким образом, применение различных процедур осреднения приводит к различным средним коэффициентам теплоотдачи. Формально различие ${{\alpha }_{m}}$ и $\left\langle \alpha \right\rangle $ обусловлено перестановкой процедур осреднения и деления ${{\vartheta }_{\delta }}$ и ${{q}_{\delta }}.$ Интересно отметить, что идейно близкая ситуация возникает при описания турбулентных течений, где входящие в уравнения Навье-Стокса величины также представляются в виде суперпозиции стационарных и пульсационных слагаемых. Осреднение этих уравнений по различным процедурам приводит к различным выражениям для рейнольдсовых напряжений [11].

Отметим, что в строгой постановке задачу взаимодействия “твердое тело – жидкость” следует ставить как сопряженную кондуктивно-конвективную задачу. Для этого необходимо решать систему нестационарных уравнений Навье-Стокса и уравнение энергии в жидкости, а также нестационарное уравнение теплопроводности в теле. Система уравнений дополняется условиями теплового сопряжения – равенством температурных функций и тепловых потоков на границе соприкасающихся сред.

Условия сопряжения существенно усложняют математическое описание по сравнению с раздельным рассмотрением процессов в жидкости и теле. Приближенные аналитические решения сопряженных кондуктивно-конвективных задач в настоящее время известны лишь для стационарных условий [12]. Получение решений нестационарных задач даже с помощью современных численных методов является весьма трудоемким и затратным с точки зрения машинного времени [13]. Основной причиной указанных трудностей является наличие в сопряженной задаче двух различных характерных времен: масштаба установления потока жидкости и масштаба прогрева (охлаждения) тела, которые могут различаться на несколько порядков. Использование же постановок с априорно установившимся режимом течения и теплопередачи не обеспечивает заданную точность решения. Все это препятствует применению унифицированных вычислительных алгоритмов для эффективного решения нестационарных сопряженных кондуктивно-конвективных задач.

В рамках метода [9, 10] частная сопряженная задача заменяется на общую краевую задачу для уравнения теплопроводности в твердом теле. В качестве ГУ задается ИКТ. Качественное и количественное влияние теплофизических свойств тела на осредненную теплоотдачу определяется взаимосвязью осредненных коэффициентов теплоотдачи – $\left\langle \alpha \right\rangle $ и ${{\alpha }_{m}}.$ Определяя из решения уравнения теплопроводности фактор сопряженности и зная $\left\langle \alpha \right\rangle $ из соответствующего раздела теории конвективного теплообмена, рассчитываем осредненную теплоотдачу по формуле:

Для замыкания математического описания задачи необходимо задать на внешней поверхности пластины соответствующее ГУ.

• Условие изотермичности $\left( {{{\vartheta }_{0}} = {\text{const}}} \right)$ означает отсутствие при $x$ = 0 пульсаций температуры: $\vartheta _{0}^{'} = 0.$

• Условие адиабатичности $\left( {{{q}_{0}} = {\text{const}}} \right)$ приводит к отсутствию пульсаций теплового потока: $q_{0}^{'} = 0.$ В частном случае ${{q}_{0}} = 0$ подвод тепла к пластине осуществляется за счет объемных тепловых источников постоянной мощности: ${{q}_{V}} = {\text{const}}{\text{.}}$

Разделив обе части ГУ (6) на $\alpha ,$ после некоторых преобразований получаем:

В ГУ (10) входят следующие безразмерные величины: истинный осредненный коэффициент теплоотдачи –

пульсационная составляющая теплового потока на поверхности теплообмена – Здесь $\omega $ – частота пульсаций интенсивности теплообмена, связанная с периодом пульсаций соотношением: $\omega = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}}.$ Согласно [1, 2], величину $B$ мы будем называть ниже числом Био. Комплекс $\sqrt {\lambda c\rho } ,$ возникающий при анализе нестационарной теплопроводности в полуограниченном теле, именуется в литературе “коэффициентом тепловой активности”.

Для параболической модели теплопроводности ${{\theta }^{ \bullet }}$ находится непосредственно из гипотезы Фурье (1). В случае гиперболической модели величину ${{\theta }^{ \bullet }}$ необходимо определять из дифференциального уравнения (4), следующего из гипотезы Каттанео–Вернотте.

Осреднение обеих частей (10) по периоду колебаний дает:

Из (11) следует, что фактор сопряженности отличается от единицы на величину корреляции пульсаций ИКТ и ТФ поверхности теплообмена. Знак этой корреляции определяет качественный характер теплового влияния твердого тела на осредненную теплоотдачу.

Рассмотрим в этой связи случай охлаждения горячей пластины потоком холодной жидкости. Из физических соображений следует, что при увеличении интенсивности теплообмена ТФ поверхности падает: $~\tilde {\alpha } > 0,$ $\theta < 0.$ Наоборот, менее интенсивному теплообмену соответствует повышение ТФ: $\tilde {\alpha } < 0,\,\,\theta > 0.$ Таким образом знаки пульсаций указанных величин для всего периода колебаний оказываются противоположными. Отсюда следует неравенство: $\left\langle {\tilde {\alpha }\theta } \right\rangle < 0,$ что согласно (11) дает: $\varepsilon < 1.$ Аналогичные оценки можно сделать также и для случая нагревания холодной пластины потоком горячей жидкости. В предельном случае бесконечно большой теплопроводности тела $\left( {\lambda \to \infty ,~B \to 0} \right)$ температурные пульсации в нем будут вырождаться: $\theta \to 0.$ Тогда, подставляя в (11) $\left\langle {\tilde {\alpha }\theta } \right\rangle = 0,$ получаем $\varepsilon = 1.$ Таким образом, мы приходим к неравенствам:

Это означает, что СКТ меньше “стационарного” или в пределе равен ему.

Разделим теперь обе части (10) на $\left( {1 + \tilde {\alpha }} \right){\text{:}}$

Осредняя это равенство по периоду колебаний, получаем второе выражение для фактора сопряженности, эквивалентное (11):

Устремим к нулю коэффициент тепловой активности тела: $\sqrt {\lambda c\rho } \to 0.$ Тогда будем иметь: $B = {{\left\langle \alpha \right\rangle } \mathord{\left/ {\vphantom {{\left\langle \alpha \right\rangle } {\sqrt {\lambda c\rho \omega } }}} \right. \kern-0em} {\sqrt {\lambda c\rho \omega } }} \to \infty ,$ что согласно (12) дает: $\varepsilon = {{\left\langle {\frac{1}{{1 + \tilde {\alpha }}}} \right\rangle }^{{ - 1}}}.$ Отсюда следует, что наименьшее возможное значение величины $\varepsilon $ не зависит от числа Био и определяется только видом периодической функции $\alpha \left( t \right).$ Выполненные оценки позволяют определить диапазон изменения фактора сопряженности:

В работе [14] приведено строгое доказательство двойного неравенства (13) для общего случая двумерного гиперболического уравнения теплопроводности.

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ

Параболическая модель теплопроводности. Рассмотрим построение аналитического решения исследуемой краевой задачи для параболической модели теплопроводности. ТФ в пластине ищется в виде бесконечного функционального ряда, каждый член которого удовлетворял уравнению (2) и ГУ при $x = 0.$ Пульсации температуры и градиента температур при $x = \delta $ записываются в виде:

Здесь ${{F}_{n}},~F_{n}^{*}$ – собственные функции; ${\text{\;}}n = 1,2,3,..$ Задавая $\tilde {\alpha }$ в виде некоторой периодической функции и используя (14) в одном из алгоритмов – (11) или (12), – можно определить собственные числа ${{A}_{n}},~A_{n}^{*},$ а также искомый фактор сопряженности $\varepsilon $.

Ниже приводятся решения для трех характерных функций $\alpha \left( t \right)$ (рис. 1) для полуограниченного твердого тела⁴⁴ $~\left( {\delta \to \infty } \right).$ В этом случае влияние граничного условия на внешней поверхности пластины вырождается, а собственные функции определяются соотношениями: ${{F}_{n}} = \sqrt {n{\text{/}}2} \left( {1 + i} \right);$ $F_{n}^{*} = \sqrt {n{\text{/}}2} \left( {1 - i} \right).$

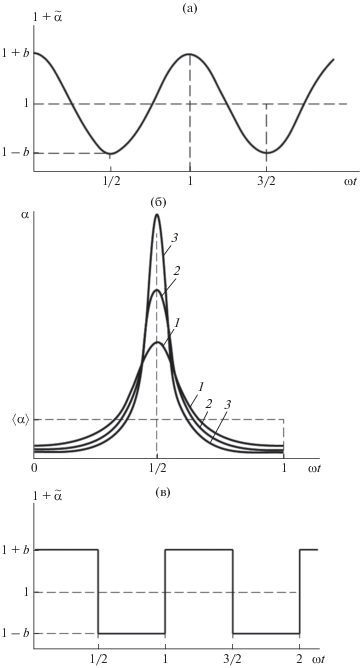
Гармоническая функция (рис. 1а) описывает гладкие симметричные колебания:

Тогда использование алгоритма (11) дает:

Здесь ${{c}_{0}} = c_{0}^{*} = 0,$ ${{c}_{n}} = {2 \mathord{\left/ {\vphantom {2 {b\left( {1 + {{{{F}_{n}}} \mathord{\left/ {\vphantom {{{{F}_{n}}} B}} \right. \kern-0em} B}} \right)}}} \right. \kern-0em} {b\left( {1 + {{{{F}_{n}}} \mathord{\left/ {\vphantom {{{{F}_{n}}} B}} \right. \kern-0em} B}} \right)}},$ $c_{n}^{*} = {2 \mathord{\left/ {\vphantom {2 {b\left( {1 + {{F_{n}^{*}} \mathord{\left/ {\vphantom {{F_{n}^{*}} B}} \right. \kern-0em} B}} \right)}}} \right. \kern-0em} {b\left( {1 + {{F_{n}^{*}} \mathord{\left/ {\vphantom {{F_{n}^{*}} B}} \right. \kern-0em} B}} \right)}}.$

Обращенная гармоническая функция (рис. 1б) характеризует гладкие асимметричные пульсации:

Здесь используется алгоритм (12):

В пределе при $b \to 1$ обращенная гармоническая функция вырождается в дельтаобразную периодическую функцию: $\alpha = \infty $ при $\omega t = \pi ;$ $\alpha = 0$ при $\omega t \ne \pi .$

Ступенчатая функция (рис. 1в) описывает разрывные симметричные колебания:

В этом случае использовались оба эквивалентные соотношения (11) и (12). Применение алгоритма (11) дает:

В свою очередь, использование алгоритма (12) приводит к эквивалентному решению:

Здесь ${{\varepsilon }_{m}} = 1 - {{b}^{2}};$ $~k = 2n - 1;$ $n = 1,2,3,...$ Полученные два решения ${{\varepsilon }_{1}},~\,\,{{\varepsilon }_{2}}~$ различались менее чем на 3%, что дает оценку максимальной относительной погрешности вычисления.

В работе [15] получено частное точное решение рассматриваемой задачи для случая моногармонических колебаний ТФ. Полагая в (14) ${{A}_{1}} = R + iI,$ $A_{1}^{*} = R - iI,$ ${{A}_{n}} = A_{n}^{*}$ = 0 $\left( {n > 1} \right),$ получаем:

Принимая $R = 0$ и используя алгоритмы (11) и (12), а также нормировку пульсаций температуры, находим неизвестные $~I,\,\,~\tilde {\alpha },\,\,~\varepsilon .$ Детальная информация об указанном решении приведена в работе [15]. Здесь следует отметить идейное сходство построения аналитических решений для характерных функций $\alpha \left( t \right)$ с методом Карташова [5, 6].

Анализ результатов. Тепловое влияние твердой стенки на осредненную теплоотдачу для случая полуограниченного тела проявляется через число Био. Для высокочастотных пульсаций интенсивности теплообмена $\left( {\omega \to \infty } \right),$ а также при больших значениях коэффициента тепловой активности тела $\left( {\sqrt {\lambda c\rho } \to \infty } \right){\text{\;}}$получаем: $B \to 0.$ В этом предельном случае пульсации температуры при $x = \delta $ становятся исчезающе малыми $\left( {{{{\tilde {\vartheta }}}_{\delta }} \to 0} \right),$ и согласно (11) мы будем иметь: ${{\alpha }_{m}} \to \alpha ,$ $\varepsilon \to 1.$ Такая же тенденция будет наблюдаться также и при исчезающе малых значениях интенсивности теплообмена: $\alpha \to 0.$

В другом предельном случае $\left( {\omega \to 0,\sqrt {\lambda c\rho } \to 0} \right)$ будем иметь: $B \to \infty .$ При этом теплоаккумулирующие способности твердого тела становятся бесконечно малыми, вследствие чего в нем будут максимально выражены пульсации температуры. Отсюда согласно (12) получаем: $\tilde {\vartheta }_{\delta }^{ \bullet }$ = 0. Здесь фактор сопряженности достигает своего минимального значения $\varepsilon = {{\varepsilon }_{m}},$ определяемого видом периодических колебаний ИКТ: $~\varepsilon = {{\left\langle {\frac{1}{{1 + \tilde {\alpha }}}} \right\rangle }^{{ - 1}}}.$ Для гармонической и обращенной гармонической функций $\alpha \left( t \right)$ это дает: ${{\varepsilon }_{m}} = \sqrt {1 - {{b}^{2}}} .$ Например, при $b = 0.9$ мы будем иметь примерно двукратное снижение осредненной теплоотдачи: ${{\alpha }_{m}} = 0.436\left\langle \alpha \right\rangle .$ Для ступенчатой функции $\alpha \left( t \right)$ при $B \to \infty $ из (12) получаем: ${{\varepsilon }_{m}} = 1 - {{b}^{2}}.$ При $b = 0.9$ это означает более чем пятикратный эффект сопряженности:$~{{\alpha }_{m}} = 0.19\left\langle \alpha \right\rangle .$

Как видно из приведенных оценок, разрывные симметричные (ступенчатые, рис. 1в) колебания интенсивности теплообмена приводят к более ярко выраженному эффекту теплового влияния по сравнению с гладкими симметричными (гармоническими, рис. 1а) колебаниями той же относительной амплитуды. Со своей стороны, симметричные и асимметричные (обращенные гармонические, рис. 1б) колебания в этом предельном случае дают один и тот же количественный эффект. Такая же тенденция будет наблюдаться также и при неограниченном возрастании интенсивности теплообмена: $\left\langle \alpha \right\rangle \to \infty .$

При исчезающе малой амплитуде пульсаций ИКТ $\left( {b \to 0} \right)$ тепловое влияние тела вырождается, и мы будем иметь: $\varepsilon \to 1$ для любого значения числа Био. Наоборот, при максимально возможной амплитуде пульсаций $\left( {b \to 1} \right)$ эффект сопряженности становится наиболее сильным.

ПРИБЛИЖЕННОЕ АНАЛИТИЧЕСКОЕ РЕШЕНИЕ

Алгоритм приближенного решения. Полученные в [9, 10] аналитические решения для характерных функций $\alpha \left( t \right)$ имеют весьма громоздкий вид. Для гармонической и обращенной гармонической функции они записываются в виде сумм бесконечных цепных дробей с комплексно-сопряженными членами, для ступенчатой функции – в виде бесконечного функционального ряда. При поиске приближенного решения будем исходить из “интегрального характера” величины $\varepsilon .$ Нас будет интересовать не ТФ на поверхности, а некоторые связанные с ней корреляции, определяемые алгоритмами (11), (12). На этом основании естественно предполагать, что при определении фактора сопряженности по алгоритму (9) погрешности расчета ТФ будут существенно сглаживаться. Используя представление (14), запишем отношение среднеквадратичных пульсаций температуры $\sqrt {\left\langle {{{\theta }^{2}}} \right\rangle } $ и теплового потока $\sqrt {\left\langle {{{\theta }^{{ \bullet 2}}}} \right\rangle } {\text{:}}$

Можно показать справедливость следующего неравенства:

Предположим, что при выполнении интегрирования можно пренебречь сдвигом фаз между пульсациями температуры и ее градиента при сохранении их амплитуд. На этой основе пишем:

Отсюда следует неравенство:

Заменяя приближенно неравенство на равенство, получаем:

Тогда, используя полученное соотношение в ГУ (10) и проводя в нем осреднение, получаем следующий алгоритм приближенного решения:

где $G = ~{{F}_{1}}F_{1}^{*}.$ В случае полуограниченного тела мы будем иметь $G = 1.$

Параболическая модель теплопроводности. Использование алгоритма (15) приводит к простым приближенным решениям для основных характерных функций $\alpha \left( t \right).$ Гармоническая функция:

обращенная гармоническая функция: ступенчатая функция:

В формулах (16)–(18) введено обозначение ${{\varepsilon }_{m}} = {{\left\langle {\frac{1}{{1 + \tilde {\alpha }}}} \right\rangle }^{{ - 1}}}$ для минимально возможного значения фактора сопряженности: ${{\varepsilon }_{m}} = \sqrt {1 - {{b}^{2}}} $ – для гармонической и обращенной гармонической функций $\alpha \left( t \right)$; ${{\varepsilon }_{m}} = 1 - {{b}^{2}}$ – для ступенчатой функции $\alpha \left( t \right)$.

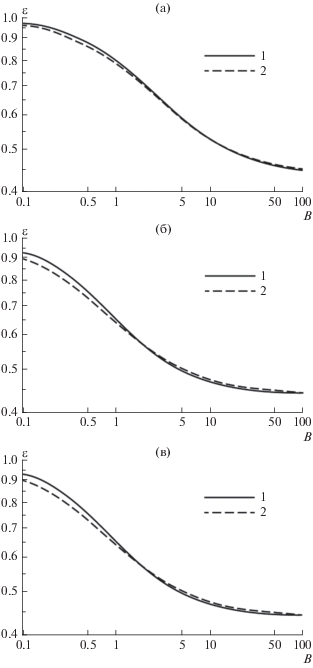
Для выяснения области применимости решений (16)–(18) проведем их сопоставление с точными аналитическими решениями. Как видно из рис. 2, при относительной амплитуде пульсаций $b = 0.9$ максимальное отклонение приближенных решений от точных не превышает 5%. При уменьшении $~b$ погрешность монотонно снижается.

На рис. 3 приведены зависимости фактора сопряженности от числа Био для различных значений относительной амплитуды пульсаций ИКТ.

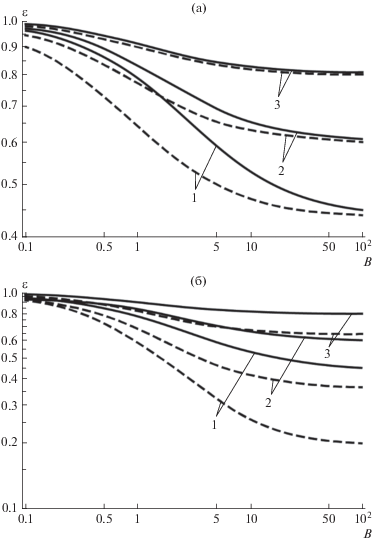
Как видно из рисунка, эффект сопряженности для обращенной гармонической функции в силу ее импульсного характера (рис. 1в) более ярко выражен, чем для симметричной гармонической функции (рис. 1а). Рис. 3 показывает резкое усиление эффекта сопряженности при переходе от гладких симметричных пульсаций (рис. 1а) к разрывной ступенчатой функции (рис. 1в).

На рис. 4 приведено сопоставление зависимостей от числа Био фактора сопряженности, представленного в виде: ${{\tilde {\varepsilon }}} = {{\left( {\varepsilon - {{\varepsilon }_{m}}} \right)} \mathord{\left/ {\vphantom {{\left( {\varepsilon - {{\varepsilon }_{m}}} \right)} {\left( {1 - {{\varepsilon }_{m}}} \right)}}} \right. \kern-0em} {\left( {1 - {{\varepsilon }_{m}}} \right)}}.$

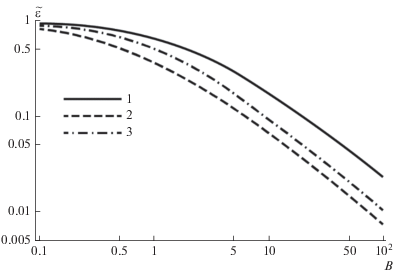
Рис. 2–4 иллюстрирует обсуждавшиеся выше качественные и количественные тенденции для различных характерных функций $\alpha \left( t \right).$ При $B \to 0$ тепловая сопряженность вырождается $\left( {\varepsilon \to 1} \right),$ при $B \to \infty $ – достигает своего максимального значения $\left( {\varepsilon \to {{\varepsilon }_{m}}} \right).$

Гиперболическая модель теплопроводности. В работе [16] представлены аналитические решения гиперболического уравнения теплопроводности в виде новых интегральных соотношений, удобных для проведения численных исследований. Доказана эквивалентность полученных результатов и имеющихся классических решений. Проведен анализ характерных особенностей аналитических решений гиперболических моделей переноса тепла.

Как известно [16], в настоящее время не существует точных аналитических решений гиперболического уравнения теплопроводности с нестационарным ГУ третьего рода. Приведем в этой связи вывод автора [6], сделанный на основе анализа параболической модели теплопроводности: “Решение класса такого рода зависимостей $\alpha \left( t \right)$ представляет собой одну из открытых проблем аналитической теории теплопроводности для краевых задач нестационарного тепло- и массопереноса с переменным во времени относительным коэффициентом теплообмена (массообмена). Дальнейшее развитие этой проблемы – переход к теории теплопроводности на основе гипотезы Максвелла–Каттанео–Лыкова–Вернотта”.

На основании сказанного выше применим для случая гиперболической модели теплопроводности развитый в [9, 10] приближенный метод. Для этого пульсации ТФ и градиента температур на поверхности теплообмена записываются в виде (14). Тогда собственные функции задачи будут равны:

Здесь ${{\beta }_{n}} = \sqrt {n{\text{/}}2} {{\left[ {{{{\left( {{{n}^{2}}{{\sigma }^{2}} + 1} \right)}}^{{1{\text{/}}2}}} - \sigma } \right]}^{{1{\text{/}}2}}};$ ${{\gamma }_{n}} = \sqrt {n{\text{/}}2} {{\left[ {{{{\left( {{{n}^{2}}{{\sigma }^{2}} + 1} \right)}}^{{1{\text{/}}2}}} + \sigma } \right]}^{{1{\text{/}}2}}};$ $n = 1,2,3,...$ Ключевую роль в анализе гиперболической модели теплопроводности играет “параметр релаксации” – описывающий степень влияния инерционности теплового потока на фактор сопряженности. В рассматриваемом случае в алгоритме (15) мы пишем:

Тогда приближенные решения для характерных законов пульсаций будут записываться в виде соотношений (16)–(18) с заменой числа Био на его модифицированный вариант:

Это выражение можно представить в более наглядном виде:

где ${{t}_{*}} = \sqrt {t_{0}^{2} + t_{r}^{2}} $ – эквивалентный период пульсаций.

Согласно полученному результату, учет времени релаксации приводит к суммарному увеличению периода пульсаций теплообмена, тем самым увеличивая эффективное число Био. Отмеченное свойство приближенного решения приводит к интересному физическому следствию. Пусть в потоке генерируются высокочастотные колебания интенсивности теплообмена. В рамках параболической модели теплообмена это приводит к вырождению теплового влияния тела: $\omega \to \infty ;$ $\varepsilon \to 1.$ В то же время учет конечной скорости распространения тепла при ${{t}_{r}} \gg {{t}_{0}}$ может приводить к заметному снижению фактора сопряженности за счет эффекта увеличения периода пульсаций. Таким образом, любое высокочастотное возмущение колебаний с периодом ${{t}_{0}} \ll {{t}_{r}}$ приводит к “эффекту самораскачки” пульсаций. Оно запускает механизм виртуальных колебаний с периодом ${{t}_{r}},$ тем самым усиливая тепловое влияние твердого тела.

Следует специально подчеркнуть, что отмеченный “эффект самораскачки” получен как результат использования приближенного алгоритма (15). Так как валидация алгоритма проводилась лишь для параболической модели теплопроводности, то результат его применения для гиперболической модели носит предварительный характер.

На рис. 5 приведены зависимости $\varepsilon \left( B \right)$ для различных значений параметра релаксации. Как видно из рисунка, при $\sigma \to 0$ эти решения асимптотически переходят в приведенные выше решения для параболической модели теплопроводности. При увеличении $\sigma $ все кривые $\varepsilon \left( B \right)$ смещаются вниз, что соответствует усилению эффекта сопряженности. При ${{t}_{r}} \to \infty $ (т.е. при $\left. {{{t}_{r}} \gg {{t}_{0}}} \right)$ модифицированное числа Био перестает зависеть от периода пульсаций и стремится к асимптотическому выражению:

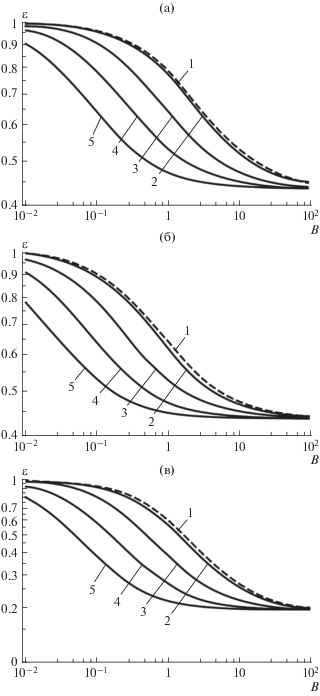
В этом предельном случае гиперболическое уравнение теплопроводности (5) переходит в волновое уравнение [1, 2]:

Рис. 6 отражает расчетные зависимости $\varepsilon \left( \sigma \right)$ при фиксированных значениях $B$. Как видно из рисунка, для каждого значения числа Био увеличение параметра релаксации ведет к снижению $\varepsilon ,$ т.е. согласно (9) – к увеличению теплового влияния твердого тела.

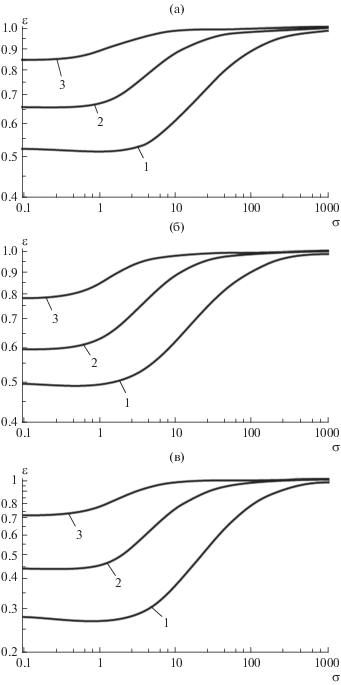
Анализ асимптотик решения. Проведем анализ эффекта сопряженности для гиперболической модели теплопроводности. Будем использовать для этого ступенчатую функцию $\alpha \left( t \right)$ с максимальной амплитудой колебаний $\left( {b = 1} \right){\text{:}}$

Для этого предельного случая будем иметь простое приближенное решение:

или, с учетом (9):

Как следует из этого равенства, результирующее термическое сопротивление ${1 \mathord{\left/ {\vphantom {1 {{{\alpha }_{m}}}}} \right. \kern-0em} {{{\alpha }_{m}}}}$ представляет собой сумму термических сопротивлений – стационарного $1{\text{/}}\left\langle \alpha \right\rangle $ и сопряженного $\sqrt {{{{{t}_{*}}} \mathord{\left/ {\vphantom {{{{t}_{*}}} {2\pi \lambda c\rho }}} \right. \kern-0em} {2\pi \lambda c\rho }}} .$ Здесь интересно отметить аналогию с известным правилом сложения термических сопротивлений в теории стационарной теплопроводности [17].

При ${{t}_{r}} \to 0$ реализуется предельный случай, описываемый параболическим уравнением теплопроводности (3):

Это выражение, в свою очередь, имеет две асимптотики. При $\sqrt {\lambda c\rho } \to \infty $ термическое сопротивление тела вырождается, и СКТ равен истинному осредненному: ${{\alpha }_{m}} \to \left\langle \alpha \right\rangle .$ Наоборот, в случае $\sqrt {\lambda c\rho } \to 0$ преобладающим становится тепловое влияние тела: ${{\alpha }_{m}} \to {{\alpha }_{w}}$. Асимптотика ${{t}_{r}} \to \infty $ соответствует случаю “предельной гиперболичности”, описываемому волновым уравнением (19)

Наконец, протяженная промежуточная область – $0 < \omega {{t}_{r}} < \infty $ – описывается гиперболическим уравнением (5).

ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ

Скачок температур. В большинстве исследований традиционно полагалось, что скорость переноса тепла имеет порядок скорости звука $w.$ Это означает, что время релаксации является характеристикой вещества, которую можно оценить как ${{t}_{r}}{\text{\;}} \approx {a \mathord{\left/ {\vphantom {a {{{w}^{2}}}}} \right. \kern-0em} {{{w}^{2}}}}.$ Для твердых тел, жидкостей и газов это дает диапазон ${{t}_{r}} \approx {{10}^{{ - 12}}} \ldots {{10}^{{ - 8}}}$ с. На основании таких оценок обычно делался вывод о пренебрежимо малой роли тепловой релаксации для большинства практических задач.

По-видимому, впервые это утверждение было подвергнуто сомнению в экспериментах [18] по измерению ТФ в телах с пространственно-неоднородной структурой. В указанной работе были проведены опыты с набросом температуры на границе массивного образца с засыпкой (мокрый песка, пищевая сода, стеклянные шарики) в воздушной сплошной среде. На основе анализа распределения температур в теле было получено значение времени релаксации в интервале ${{t}_{r}} \approx $ 10…54 с. В работе [19] по результатам измерения нестационарного поля температур при контакте двух образцов биологической ткани с различной начальной температурной функцией было получено: ${{t}_{r}} \approx $ 15 с. В противоречие с указанными выводами вступили экспериментальные данные работ [20, 21]. Обработка их результатов показала применимость классического закона Фурье, в том числе для тел с неоднородной внутренней структурой.

Гармонические температурные пульсации. Ясность в вопрос экспериментального определения времени релаксации внесли авторы [22]. Они провели сравнительный анализ работ [18–21] и выявили присущие им недостатки при проведении эксперимента и последующей обработке опытных данных. В работе [22] была проведена серия тестовых опытов по одновременному измерению эффективной температуропроводности среды ${{a}_{e}}$ и времени релаксации ${{t}_{r}}$ в ходе одного эксперимента.

Исследуемый образец представлял собой цилиндр диаметром 40 мм и высотой 80 мм. В качестве засыпки использовались различные среды: свинцовые шарики с медным покрытием диаметром 4.4 мм; искусственный песок; порошок оксида алюминия с частицами различного размера; порошок гидроксида натрия; биологическая ткань. Газовыми наполнителями сыпучей среды служили: воздух; гелий; азот; аргон. В опытах варьировались давление и температура газа. На поверхности образца с помощью элемента Пельтье генерировались гармонические пульсации ТФ, которые измерялись шестью термопарами, расположенными на оси образца с шагом 10 мм. Определялись декремент затухания амплитуды и фазовый сдвиг пульсаций, которые сопоставлялись с результатами аналитического решения гиперболического уравнения теплопроводности для полуограниченного тела. Найденные таким образом значения ${{a}_{e}},{{t}_{r}}$ сопоставлялись с данными других авторов. Как видно из табл. 1, полученные в [22] значения ${{t}_{r}}$ оказались примерно на порядок меньшими, чем в работах [18, 19].

Оценка времени релаксации. Из физических соображений следует, что зафиксированные в работах [18, 19, 22] аномально высокие значения времени релаксации обусловлены спецификой теплопереноса в пространственно-неоднородных средах. Так как механизм теплопроводности в засыпке частиц затруднен в силу их точечного контакта, определяющую роль должен играть здесь процесс свободной конвекции в газовом наполнителе. В экспериментах [22] показано, что эффективная теплопроводность образца слоя сильно зависит от размера частиц и типа их упаковки в засыпке. Ввиду огромного различия (более десяти порядков!) в значениях времени релаксации, полученных в работах [17–21], методически полезно провести приближенную оценку ${{t}_{r}}.$ Согласно опытам [22], для засыпки из свинцовых шариков диаметром ${{d}_{0}}$ = 4.4 мм при атмосферном давлении (газовые наполнители – аргон и азот) были получены следующие результаты: ${{a}_{e}}$ ≈ 8 × 10^–6 м²/с; ${{t}_{r}}$ ≈ 14 с.

Будем исходить из модели неоднородной среды, составленной из сферических элементарных ячеек. Воспользуемся полученным в работе [23] аналитическим решением задачи теплопроводности на основе интегрального метода теплового баланса. В указанной работе рассматривался процесс нагрева холодного шара диаметром ${{d}_{0}}$ при мгновенном увеличении ТФ его поверхности на величину ${{\vartheta }_{s}}.$ В результате было получено следующее выражение для разности температур:

где ${{\vartheta }_{0}}\left( t \right)$ – температура в центре шара.

Так как ячейка включает в себя собственно шарик и окружающий его газ, положим ее диаметр равным удвоенному диаметру шарика в засыпке ${{d}_{0}}$ = 8.8 мм. Примем за время релаксации такое время, за которое центр шара прогреется на 95%: ${{\vartheta }_{0}} = 0.95{{\vartheta }_{s}};$ Δ = 0.05. Тогда получаем: ${{t}_{r}} \approx {{0.107d_{0}^{2}} \mathord{\left/ {\vphantom {{0.107d_{0}^{2}} {{{a}_{e}}}}} \right. \kern-0em} {{{a}_{e}}}}.$ Использование в этой формуле приведенных выше параметров работы [22] дает: ${{t}_{r}}$ ≈ 10.4 с. Проведенные оценки позволяют дать качественное объяснение упомянутому выше огромному различию в численных значениях ${{t}_{r}}$ в однородной и неоднородной средах.

Оценка фактора сопряженности. К веществам, имеющим неоднородную внутреннюю структуру, относятся также полимеры, состоящие из мономерных звеньев, соединенных в длинные макромолекулы химическими или координационными связями. В работе [24] экспериментально исследовался переходный термический процесс в центре пластины, выполненной из полимерного материала (полиметилметакрилата) при ее внезапном погружении в горячую дистиллированную воду. Было установлено, что температура в центре пластины в течение некоторой временной паузы $\left( {{{t}_{r}} \approx 3.5~\,{\text{с}}} \right)$ остается неизменной и равной начальной температуре.

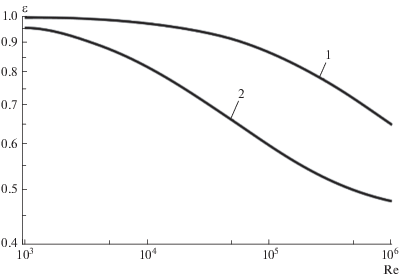
Свойства полиметилметакрилата хорошо изучены, поэтому представляет интерес оценить применительно к опытам [24] значение фактора сопряженности для “волновой асимптотики” (19). Термическое сопротивление сопряженности рассчитывается по формуле $\sqrt {{{{{t}_{r}}} \mathord{\left/ {\vphantom {{{{t}_{r}}} {2\pi \lambda c\rho }}} \right. \kern-0em} {2\pi \lambda c\rho }}} .$ Рассмотрим случай турбулентного течения воды в прямой круглой трубе диаметром $d$ при атмосферном давлении и температуре 20°С. Для расчета стационарного термического сопротивления $1{\text{/}}\left\langle \alpha \right\rangle $ будем использовать известную формулу Диттуса–Болтера [25] для стационарного коэффициента теплоотдачи:

Здесь ${\text{Nu}} = {{\left\langle \alpha \right\rangle d} \mathord{\left/ {\vphantom {{\left\langle \alpha \right\rangle d} {{{\lambda }_{f}}}}} \right. \kern-0em} {{{\lambda }_{f}}}}$ – число Нуссельта; ${\text{Re}} = {{ud} \mathord{\left/ {\vphantom {{ud} {{{\nu }_{f}}}}} \right. \kern-0em} {{{\nu }_{f}}}}$ – число Рейнольдса; ${\text{Pr}} = {{{{\nu }_{f}}} \mathord{\left/ {\vphantom {{{{\nu }_{f}}} {{{a}_{f}}}}} \right. \kern-0em} {{{a}_{f}}}}$ – число Прандтля; $u$ – скорость потока; $d$ – диаметр трубы; ${{\lambda }_{f}},~{{\nu }_{f}},~{{a}_{f}}$ – соответственно теплопроводность, кинематическая вязкость и температуропроводность жидкой среды.

Примем, что расход жидкости (а следовательно, и ИКТ) изменяется во времени по гармоническому закону. На рис. 7 приведены расчетные кривые зависимости фактора сопряженности от числа Рейнольдса при двух значениях диаметра. Как видно из рисунка, при увеличении числа Рейнольдса значение СКТ заметно уменьшается. Тепловое влияние твердого тела усиливается при уменьшении диаметра трубы. Так, при ${\text{Re}} = {{10}^{6}}$ имеем: ${{\alpha }_{m}} = 0.474\left\langle \alpha \right\rangle .$

ЗАКЛЮЧЕНИЕ

Проведен анализ теплового влияния характеристик твердого тела на стандартный коэффициент теплоотдачи, измеряемый в традиционном теплообменном эксперименте и используемый в прикладных расчетах. Метод анализа процессов теплообмена с периодической интенсивностью, разработанный ранее для параболической модели теплопроводности, обобщен на случай конечной скорости распространения тепла. Частная сопряженная задача для системы “твердое тело–жидкость” заменяется на общую краевую задачу для гиперболического уравнения теплопроводности в теле. Для случая полуограниченного тела получены приближенные решения для характерных типов пульсаций интенсивности теплообмена: гармонического, обращенного гармонического и ступенчатого. Аналитическое решение для фактора сопряженности для гиперболической модели теплопроводности записывается в том же виде, что и полученное ранее “параболическое решение”. При этом входящее в итоговые выражения для характерных задач число Био заменяется на модифицированное выражение, включающее параметр релаксации. Представлены зависимости фактора сопряженности от числа Био, амплитуды колебаний интенсивности теплообмена, а также от параметра релаксации теплового потока. Показано, что учет конечной скорости распространения тепла приводит к увеличению эффекта сопряженности. Получено, что для предельного случая волнового уравнения теплопроводности тепловое влияние твердого тела неограниченно возрастает. Проведен анализ асимптотик решения, позволяющий описать физическую картину влияния конечной скорости распространения тепла на осредненную теплоотдачу при периодических пульсациях ее интенсивности. Показано, что в рамках гиперболической модели теплопроводности имеет место “эффект самораскачки” пульсаций, обусловленный “удлинением периода” колебаний и приводящий к усилению теплового влияния твердого тела. Обнаружение указанного эффекта носит предварительный характер и требует дальнейшего исследования.

Сокращения: ГУ – граничные условия; ИКТ – истинный коэффициент теплоотдачи; СКТ – стандартный коэффициент теплоотдачи; ТФ – температурная функция.

Обозначения: ${{A}_{n}},~A_{n}^{*}$ – собственные числа; $a$ – коэффициент температуропроводности; $B$ – число Био; ${{B}_{*}}$ – модифицированное число Био; $b$ – амплитуда пульсаций истинного коэффициента теплоотдачи; ${{F}_{n}},~F_{n}^{*}$ – собственные функции; $c$ – теплоемкость; $q$ – тепловой поток; ${{q}_{V}}$ – объемная плотность тепловых источников; $\rho $ – плотность; $t$ – время; ${{t}_{0}}$ – период пульсаций истинного коэффициента теплоотдачи; ${{t}_{*}}$ – эквивалентный период пульсаций истинного коэффициента теплоотдачи; ${{t}_{r}}$ – время релаксации; $x$ – координата.

Греческие символы: $\alpha $ – истинный коэффициент теплоотдачи; $\left\langle \alpha \right\rangle $ – истинный осредненный коэффициент теплоотдачи; ${{\alpha }_{m}}$ – стандартный коэффициент теплоотдачи; $\tilde {\alpha }$ – безразмерная пульсация истинного коэффициента теплоотдачи; $\varepsilon $ – фактор сопряженности; ${{\varepsilon }_{m}}$ – минимальное значение фактора сопряженности; $\lambda $ – коэффициент теплопроводности; $\theta $ – безразмерная пульсация температуры на поверхности теплообмена; ${{\theta }^{ \bullet }}$ – безразмерная пульсация градиента температуры на поверхности теплообмена; $\omega $ – частота пульсаций истинного коэффициента теплоотдачи; $\rho $ – плотность; $\sigma $ – параметр релаксации; $\vartheta $ – температурная функция.

Верхние индексы: ' – пульсационная величина;

Нижние индексы: $\delta $ – значение на поверхности теплообмена; $f$ – относящийся к жидкой среде.