Известия РАН. Энергетика, 2022, № 3, стр. 49-62

О необходимости учета пространственной когерентности при совместной цифровой обработке пространственно-разнесенных сигналов токов и напряжений в электрических сетях

А. Л. Куликов¹, П. В. Илюшин^2, *, А. А. Севостьянов¹

¹ ФГБОУВО “Нижегородский государственный технический университет им. Р.Е. Алексеева”
Нижний Новгород, Россия

² ФГБУН Институт энергетических исследований Российской академии наук
Москва, Россия

^* E-mail: ilyushin.pv@mail.ru

Поступила в редакцию 23.11.2021
После доработки 02.02.2022
Принята к публикации 15.02.2022

EDN: ZLYQEV
DOI: 10.31857/S0002331022030037

Полный текст (PDF)

Аннотация

В условиях децентрализации энергетики в электрических сетях наблюдаются отклонения показателей качества электроэнергии (ПКЭЭ), включая нарушения синусоидальности сигналов токов и напряжений. Это приводит к росту ошибок при совместной цифровой обработке пространственно-разнесенных сигналов в цифровых устройствах. Приведены особенности использования понятия пространственной когерентности при измерениях и цифровой обработке сигналов токов и напряжений. Рассмотрены методы оценки когерентности сигналов токов и напряжений при синхронизированных измерениях в условиях отклонения ПКЭЭ. На примере реализации двухстороннего определения мест повреждения (ОМП) на линии электропередачи (ЛЭП) показано, что чем меньше коэффициент взаимной корреляции, тем выше ошибка и ниже точность расчета расстояния до места повреждения. Характер влияния нарушений пространственной когерентности на ошибки ОМП ЛЭП зависит от используемого выражения для расчета расстояния до места повреждения. Обосновано применение нормированного коэффициента взаимной корреляции для фиксации ошибок цифровой обработки сигналов токов и напряжений при нарушениях пространственной когерентности. Исследовано влияние интергармоник и шумов на ошибки ОМП ЛЭП при нарушениях пространственной когерентности сигналов. Расчетами доказано, что величина искажений и ошибки оценки амплитуды тока и напряжения зависят от соотношения амплитуд и фаз основной и искажающих интергармоник. Показано, что применение фильтрации исходного и прореженного сигналов на основе дискретного преобразования Фурье обеспечивает исключение шумовых составляющих из гармоники промышленной частоты.

Ключевые слова: пространственная когерентность, нормированный коэффициент взаимной корреляции, показатели качества электрической энергии, синхронизированные измерения, определение места повреждения

ВВЕДЕНИЕ

Понятие “когерентность” является основополагающим и используется в различных технических приложениях, связанных с флюктуирующими физическими величинами. При этом “когерентность” имеет особенности применения для решения различных прикладных задач, в том числе в электрических сетях [1–4].

Тренд на децентрализацию энергетики приводит к массовой интеграции в энергосистемы разнородных объектов распределенной генерации, в том числе возобновляемых источников энергии, и другого электрооборудования с элементами силовой электроники. Они оказывают существенное влияние установившиеся режимы, характер и параметры переходных процессов, а также ПКЭЭ, включая синусоидальность токов и напряжений. Поэтому выбор адекватного подхода к оценке когерентности сигналов токов и напряжений синхронизированных измерений при отклонениях ПКЭЭ актуален [5–7].

Пространственная когерентность играет важную роль при использовании массивов пространственно-распределенных измерений искаженных сигналов токов и напряжений в ветвях и узлах сети [8–11]. Если массив измерений рассматривается как матрица выборочных значений пространственно-временной осциллограммы, то пространственная когерентность используется для формирования линейных комбинаций из пространственных выборок. Популярными алгоритмами обработки пространственно-когерентных сигналов являются MUSIC и ESPRIT [12–14].

Рассмотрим массив синхронизированных измерений токов и напряжений в n точках электрической сети с помощью n соответствующих датчиков, образующих n-мерный вектор y(t) = {y(t, ζ₁), y(t, ζ₂), … , y(t, ζ_n)} аналитических сигналов, где точки {ζ₁, ζ₂, …, ζ_n} представляют собой пространственное расположение n датчиков [15]. В общем случае сигналы могут быть смоделированы с приближением как

(1)

$y\left( t \right) = As{\kern 1pt} \left( t \right) + n\left( t \right),$

где A – матрица размером n × d, столбцы которой {a(θ_i): i = 1, 2, …, d} – векторы, связанные с d сигналами [элементы s(t)], имеющими соответствующий массив {θ_i: i = 1, 2, …, d} начальных фаз; n(t) – аддитивный датчик шума.

Для дискретизированных сигналов токов и напряжений задача существенно усложняется, так как сигналы задаются не в аналитической форме, а соответствующими векторами мгновенных значений или в комплексной форме, представляющими собой совокупность выборок на интервале наблюдения.

Целью статьи является обоснование необходимости использования нормированного коэффициента взаимной корреляции для фиксации и учета ошибок цифровой обработки сигналов токов и напряжений в цифровых устройствах, размещенных в разных узлах сети.

МЕТОД ОЦЕНКИ СТЕПЕНИ КОГЕРЕНТНОСТИ ПРОСТРАНСТВЕННО-РАЗНЕСЕННЫХ КОМПЛЕКСНЫХ СИНУСОИДАЛЬНЫХ СИГНАЛОВ

Рассмотрим случай сопоставления двух дискретизированных сигналов напряжения. Предположим, что x(t) и y (t) представляют собой измерения одиночных сигналов u(t, ζ) в двух различных пространственных точках ζ₁ и ζ₂:

(2)

$x\left( t \right) = u(t,{{\zeta }_{1}}),y{\kern 1pt} \left( t \right) = u(t,{{\zeta }_{2}}).$

В более общем случае x(t) и y(t) могут представлять выборки u(t, ζ) в двух различных точках пространства в разные моменты времени

(3)

$x(t) = u(t - {{t}_{1}},{{\zeta }_{1}}),y(t) = u(t - {{t}_{2}},{{\zeta }_{2}}).$

Определим взаимную когерентность между двумя пространственно-временными осциллограммами x(t, ζ) и y(t, ζ).

Перейдем к комплексным дискретизированным сигналам напряжения с частотой дискретизации f_д = 1/Т_д, наблюдаемым на интервале времени из N (k = 0, …, N – 1) отсчетов, исключив индекс ζ. Синхронизированное представление сигналов напряжения при отклонении ПКЭЭ соответствует выражениям

(4)

$x(k,{{\psi }_{1}}) = {{\upsilon }_{1}}(k)\cos (2\pi {{f}_{0}}k{{T}_{{\text{д}}}} + {{\varphi }_{1}}(k) + {{\psi }_{1}}),$

(5)

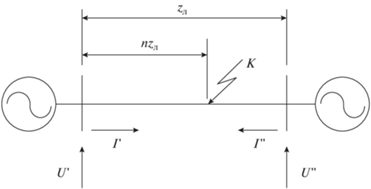
$у(k,{{\psi }_{2}}) = {{\upsilon }_{2}}(k)\cos (2\pi {{f}_{0}}k{{T}_{{\text{д}}}} + {{\varphi }_{2}}(k) + {{\psi }_{2}}),$

где φ₁(k) и φ₂(k) – законы изменения фазы (частоты); ψ₁ и ψ₂ – начальные фазы сигналов напряжения; f₀ – промышленная частота.

Законы изменения фазы (частоты) φ₁(k) и φ₂(k) соответствуют расхождению ЭДС источников питания, например, по концам линии электропередачи (ЛЭП) при коротком замыкании на ней (рис. 1). При несинхронизированном представлении сигналов в выражения (4) и (5) вводятся дискретные задержки.

Рис. 1.

Упрощенная однолинейная схема ЛЭП при КЗ.

Комплексные векторы (амплитуды) для выражений (4) и (5) сигналов x(k, ψ₁) и у(k, ψ₂) принимают вид

(6)

${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }_{1}}(k,{\text{ }}{{\psi }_{1}}) = {{\upsilon }_{1}}(k){\text{ехр}}\{ j{{\varphi }_{1}}(k)\} {\text{ехр}}\{ j{{\psi }_{1}}\} = {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }_{1}}(k){\text{ехр}}\{ j{{\psi }_{1}}\} ,$

(7)

${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }_{2}}(k,{{\psi }_{2}}) = {{\upsilon }_{2}}(k){\text{ехр}}\{ j{{\varphi }_{2}}(k)\} {\text{ехр}}\{ j{{\psi }_{2}}\} = {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }_{2}}(k){\text{ехр}}\{ j{{\psi }_{2}}\} ,$

где υ₁(k) = υ₁(k, 0), υ₂(k) = υ₂(k, 0).

Определим коэффициент корреляции между дискретными сигналами на интервале наблюдения из N отсчетов

(8)

$\begin{gathered} ~R\left( {{{\psi }_{1}},{{\psi }_{2}}} \right) = \mathop \sum \limits_{k = 0}^{N - 1} x(k,{{\psi }_{1}})у(k,{{\psi }_{2}}) = \\ = \mathop \sum \limits_{k = 0}^{N - 1} R{\kern 1pt} e[{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{1}}(k,{{\psi }_{1}})\exp \{ 2\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} ]R{\kern 1pt} e[{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{2}}(k,{{\psi }_{2}})\exp \{ 2\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} ]. \\ \end{gathered} $

Запишем действительную часть числа в виде Re[q] = (q + q*)/2, тогда выражение (8) можно представить в виде

(9)

$\begin{gathered} \left( {1/4} \right)\mathop \sum \limits_{k = 0}^{N - 1} \text{[}{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{1}}(k,{{\psi }_{1}})\exp \{ 2\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} + \upsilon _{1}^{*}(k,{{\psi }_{1}})\exp \{ - 2\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} ][{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{2}}(k,{{\psi }_{2}})\exp \{ 2\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} + \\ + \,\,\upsilon _{2}^{*}(k,{{\psi }_{2}})\exp \{ - 2\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} ] = \left( {1{\text{/}}4} \right)\mathop \sum \limits_{k = 0}^{N - 1} [{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{1}}(k,{{\psi }_{1}}){{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{2}}(k,{{\psi }_{2}}){\text{exp}}\{ 4\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} + \\ + \,\,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{1}^{*}(k,{{\psi }_{1}})\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{2}^{*}(k,{{\psi }_{2}}){\text{exp}}\{ - 4\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} ] + \left( {1{\text{/}}4} \right)\mathop \sum \limits_{k = 0}^{N - 1} [{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{1}}(k,{{\psi }_{1}})\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{2}^{*}(k,{{\psi }_{2}}){\text{ }} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{1}^{*}(k,{{\psi }_{1}}){{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{2}}(k,{{\psi }_{2}})] = \\ = \left( {1{\text{/}}2} \right)\mathop \sum \limits_{k = 0}^{N - 1} Re[{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{1}}(k,{{\psi }_{1}}){{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{2}}(k,{{\psi }_{2}}){\text{exp}}\{ 4\pi {{f}_{0}}k{{T}_{{\text{д}}}}\} + \left( {1{\text{/}}2} \right)\mathop \sum \limits_{k = 0}^{N - 1} Re[{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{1}}(k,{{\psi }_{1}})\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{2}^{*}(k,{{\psi }_{2}})]. \\ \end{gathered} $

Первой групповой суммой в равенстве (9) можно пренебречь, поскольку она соответствует суммированию мгновенных значений относительно быстро осциллирующей функции [16]. Тогда итоговое соотношение для комплексного коэффициента корреляции принимает вид

(10)

$R\left( {{{\psi }_{1}},{{\psi }_{2}}} \right) = \left( {1{\text{/}}2} \right)\sum\limits_{k = 0}^{N - 1} {Re} [{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }_{1}}(k,{{\psi }_{1}})\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } {{_{2}^{*}}_{2}}(k,{{\psi }_{2}})] = \left( {1{\text{/}}2} \right)Re\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {{{\psi }_{1}},{{\psi }_{2}}} \right).$

В выражении (10) комплексный коэффициент корреляции огибающих ρ равен

(11)

$~\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {{{\psi }_{1}},{{\psi }_{2}}} \right) = \mathop \sum \limits_{k = 0}^{N - 1} {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }_{1}}(k,{{\psi }_{1}})\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{2}^{*}(k,{{\psi }_{2}}) = \exp \{ j\left( {{{\psi }_{1}} - {{\psi }_{2}}} \right)\} \mathop \sum \limits_{k = 0}^{N - 1} {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }_{1}}(k)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{2}^{*}(k) = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \exp \{ j\left( {{{\psi }_{1}} - {{\psi }_{2}}} \right)\} ,$

где

(12)

$~\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {0.0} \right) = \mathop \sum \limits_{k = 0}^{N - 1} {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }_{1}}(k)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{2}^{*}(k) = \rho \exp \{ j\beta \} ,$

а ρ и β – модуль и аргумент коэффициента корреляции.

Используя введенные обозначения, преобразуем (10) к равенству

(13)

$R\left( {{{\psi }_{1}},{{\psi }_{2}}} \right) = \left( {1{\text{/}}2} \right)\rho \cos (\beta + {{\psi }_{1}} - {{\psi }_{2}}).$

Анализ выражения (13) показывает, что из-за неопределенности фаз коэффициент корреляции является неопределенной величиной, что не позволяет его использовать для сравнения рассматриваемых сигналов. Тем не менее модуль коэффициента корреляции не зависит от углов ψ₁ и ψ₂

(14)

$~\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {{{\psi }_{1}},{{\psi }_{2}}} \right)} \right| = \rho = \left| {\mathop \sum \limits_{k = 0}^{N - 1} {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{1}}(k,{{\psi }_{1}})\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{2}^{*}(k,{{\psi }_{2}})} \right| = \left| {\mathop \sum \limits_{k = 0}^{N - 1} {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } }}_{1}}(k)\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\upsilon } _{2}^{*}(k)} \right|.$

Поэтому его можно использовать для оценки соответствия (степени похожести) дискретных сигналов между собой.

Определим совокупность операций обработки для формирования модульного значения коэффициента корреляции. Примем, что дискретный сигнал

(15)

$x(k) = x(k,0) = {{\upsilon }_{1}}(k)\cos (2\pi {{f}_{0}}k{{T}_{{\text{д}}}} + {{\varphi }_{1}}(k))$

является эталонным и заранее известным. Так как коэффициент корреляции зависит от разности начальных фаз анализируемых сигналов, то в общем случае можно выбрать нулевую начальную фазу (ψ₁ = 0) сигнала x(k). Тогда выражение для модуля коэффициента корреляции примет вид

(16)

$\left| {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {{{\psi }_{1}},{{\psi }_{2}}} \right)} \right| = \rho = {\text{sqrt}}{{\{ {{[Re\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {0,{{\psi }_{2}}} \right)]}^{2}} + Im\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {0,{{\psi }_{2}}} \right)]}^{2}}\} .$

Определим действительную часть комплексного коэффициента корреляции

(17)

$~Re\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {0,{{\psi }_{2}}} \right) = 2R\left( {0,{{\psi }_{2}}} \right) = 2\mathop \sum \limits_{k = 0}^{N - 1} x(k)у(k,{{\psi }_{2}}).$

Для оценки мнимой части комплексного коэффициента корреляции примем ψ₁ = –π/2

(18)

$\begin{gathered} \hfill R\left( { - \pi {\text{/}}2,{{\psi }_{2}}} \right) = \left( {1{\text{/}}2} \right)Re\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } (\left( { - \pi {\text{/}}2,{{\psi }_{2}}} \right) = \left( {1{\text{/}}2} \right)Re\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \exp \{ - j{{\psi }_{2}}\} \exp \{ - j\pi {\text{/}}2\} = \\ \hfill = \left( {1{\text{/}}2} \right)Re( - j\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \exp \{ - j{{\psi }_{2}}\} ) = \left( {1{\text{/}}2} \right)Re( - j\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } (0,{{\psi }_{2}})) = \left( {1{\text{/}}2} \right)Im(\rho (0,{{\psi }_{2}})), \\ \end{gathered} $

где

$~Im(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } (0,{{\psi }_{2}})) = 2R\left( { - \pi {\text{/}}2,{{\psi }_{2}}} \right) = 2\mathop \sum \limits_{k = 0}^{N - 1} x(k, - \pi {\text{/}}2)у(k,{{\psi }_{2}}) = 2\mathop \sum \limits_{k = 0}^{N - 1} {{x}_{s}}\left( k \right)у(k,{{\psi }_{2}}),$

причем

(19)

${{x}_{s}}(k) = x(k, - \pi {\text{/}}2) = {{\upsilon }_{1}}(k)\cos (2\pi {{f}_{0}}k{{T}_{{\text{д}}}} + {{\varphi }_{1}}(k) - \pi {\text{/}}2) = {{\upsilon }_{1}}(k)\sin (2\pi {{f}_{0}}k{{T}_{{\text{д}}}} + {{\varphi }_{1}}(k)).$

Анализ выражений показывает, что структура устройства для расчета модуля коэффициента корреляции аналогична структуре устройства цифровой квадратурной обработки, применяемой в цифровой релейной защите [17, 18].

ОЦЕНКА КОМПЛЕКСНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ СИНУСОИДАЛЬНОГО СИГНАЛА, ИСКАЖЕННОГО ПОМЕХОВЫМИ КОМПОНЕНТАМИ

Сигналы токов и напряжений в электрических сетях могут быть подвержены воздействию искажающих помеховых компонент. Принимаем, что сигнал у(k, ψ₂) искажен дискретным белым шумом n(k) с постоянной спектральной плотностью мощности N₀/2 [16]

(20)

${{у}_{{\text{ш}}}}(k,{{\psi }_{2}}) = Ау(k,{{\psi }_{2}}) + n(k),$

где у(k, ψ₂) определен в соответствии с (5); А и ψ₂ – параметры сигнала у(k, ψ₂).

Сигналы x(k) и x_s(k) для вычисления комплексного коэффициента корреляции определяются по выражениям (15) и (19). Отметим, что дискретный случайный сигнал у_ш(k, ψ₂) соответствует случайному процессу с гауссовым законом распределения и математическим ожиданием М[у_ш(k, ψ₂)] = у(k, ψ₂).

При выбранных обозначениях реальная и мнимая составляющие комплексного коэффициента корреляции в дискретный момент времени k определяются следующими случайными величинами

(21)

${{w}_{{\text{R}}}} = Re\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {0,{{\psi }_{2}}} \right) = 2\mathop \sum \limits_{k = 0}^{N - 1} x(k){{у}_{{\text{ш}}}}(k,{{\psi }_{2}}),$

(22)

$~{{w}_{{\text{I}}}} = Im\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\rho } \left( {0,{{\psi }_{2}}} \right) = 2\mathop \sum \limits_{k = 0}^{N - 1} {{x}_{s}}(k){{у}_{{\text{ш}}}}(k,{{\psi }_{2}}).$

Нормальные распределения переменных w_R и w_I соответствуют выражениям

(23)

$~{{p}_{w}}_{{\text{R}}}\left( s \right) = (1{\text{/}}{{\sigma }_{w}}_{{\text{R}}}\sqrt {2\pi } )\exp \{ - {{(s - {{m}_{w}}_{{\text{R}}})}^{2}}{\text{/}}2\sigma _{{w{\text{R}}}}^{2}\} ,$

(24)

$~{{p}_{w}}_{{\text{I}}}\left( s \right) = (1{\text{/}}{{\sigma }_{w}}_{{\text{I}}}\sqrt {2\pi } )\exp \{ - {{(s - {{m}_{w}}_{{\text{I}}})}^{2}}{\text{/}}2\sigma _{{w{\text{I}}}}^{2}\} ,$

где m_wR, m_wI и $\sigma _{{w{\text{R}}}}^{2},$ $\sigma _{{w{\text{I}}}}^{2}$ – математические ожидания и дисперсии случайных величин w_R и w_I.

Математические ожидания m_wR, m_wI случайных переменных w_R и w_I являются результатами преобразований

(25)

${{m}_{w}}_{{\text{R}}} = {\text{ }}2\mathop \sum \limits_{k = 0}^{N - 1} x(k){{у}_{{\text{ш}}}}(k,{{\psi }_{2}}) = 2АRxy,$

(26)

${{m}_{w}}_{{\text{I}}} = {\text{ }}2\mathop \sum \limits_{k = 0}^{N - 1} {{x}_{s}}(k){{у}_{{\text{ш}}}}(k,{{\psi }_{2}}) = 2АR{{x}_{s}}y.$

Получим дополнительные выражения для математических ожиданий

(27)

${{m}_{w}}_{{\text{R}}} = А\rho \cos (\beta - {{\psi }_{2}}),\,\,\,\,{{m}_{w}}_{{\text{I}}} = А\rho \sin (\beta - {{\psi }_{2}}),$

где ρ и β определяются из равенства (12).

Получим дисперсии случайных величин w_R и w_I при условии равенства энергий сигналов x(k) и x_s(k). Ввиду идентичности расчетов определим дисперсию $\sigma _{{w{\text{R}}}}^{2}$ только сигнала w_R, учитывая, что величина $\sigma _{{w{\text{R}}}}^{2}$ определяется дискретной составляющей шума n(k) процесса у_ш(k, ψ₂) (20)

(28)

$\begin{gathered} ~\sigma _{{w{\text{R}}}}^{2} = D\{ {{w}_{{\text{R}}}}\} = M\left\{ {{{{\left[ {2\mathop \sum \limits_{k = 0}^{N - 1} x(k)n(k)} \right]}}^{2}}} \right\} = 4M\left\{ {\mathop \sum \limits_{k1 = 0}^{N - 1} x({{k}_{1}})n({{k}_{1}})\mathop \sum \limits_{k2 = 0}^{N - 1} x({{k}_{2}})n({{k}_{2}})} \right\} = \\ = 4M\left\{ {\mathop \sum \limits_{k2 = 0}^{N - 1} \mathop \sum \limits_{k1 = 0}^{N - 1} n({{k}_{1}})n({{k}_{2}})x({{k}_{1}})x({{k}_{2}})} \right\} = 4\mathop \sum \limits_{k2 = 0}^{N - 1} \mathop \sum \limits_{k1 = 0}^{N - 1} M\{ n({{k}_{1}})n({{k}_{2}})\} x({{k}_{1}})x({{k}_{2}}). \\ \end{gathered} $

Учитывая, что белый шум является δ – коррелированным случайным процессом, то математическое ожидание соответствует корреляционной функции шумового процесса n(k)

(29)

$M\{ n({{k}_{1}})n({{k}_{2}})\} = ({{N}_{0}}{\text{/}}2)\delta ({{k}_{2}} - {{k}_{1}}).$

Получим дисперсию сигнала w_R

(30)

$\sigma _{{w{\text{R}}}}^{2} = 4({{N}_{0}}{\text{/}}2)~\mathop \sum \limits_{k1 = 0}^{N - 1} x({{k}_{1}})~~\mathop \sum \limits_{k2 = 0}^{N - 1} \delta ({{k}_{2}} - {{k}_{1}})x({{k}_{2}}) = 2{{N}_{0}}~\mathop \sum \limits_{k1 = 0}^{N - 1} x({{k}_{1}})x({{k}_{2}}) = 2{{N}_{0}}Е,$

где Е – энергия сигнала квадратурной составляющей при вычислении комплексного коэффициента корреляции.

Коэффициент взаимной корреляции случайных величин w_R и w_I соответствует выражению

(31)

$\begin{gathered} ~{{R}_{w}}_{{{\text{R}}w{\text{I}}}} = М\{ ({{w}_{{\text{R}}}} - {{m}_{w}}_{{\text{R}}})({{w}_{{\text{I}}}} - {{m}_{w}}_{{\text{I}}})\} = 4M\left\{ {\mathop \sum \limits_{k1 = 0}^{N - 1} x({{k}_{1}})n({{k}_{1}})\mathop \sum \limits_{k2 = 0}^{N - 1} {{x}_{s}}({{k}_{2}})n({{k}_{2}})} \right\} = \\ = 4\mathop \sum \limits_{k2 = 0}^{N - 1} \mathop \sum \limits_{k1 = 0}^{N - 1} M\{ n({{k}_{1}})n({{k}_{2}})\} x({{k}_{1}}){{x}_{s}}({{k}_{2}}). \\ \end{gathered} $

Учитывая ранее введенные преобразования, получим

(32)

$~{{R}_{w}}_{{{\text{R}}w{\text{I}}}} = 2{{N}_{0}}~\mathop \sum \limits_{k1 = 0}^{N - 1} x({{k}_{1}}){{x}_{s}}({{k}_{2}}) = 2{{N}_{0}}{{R}_{{xxs}}}.$

Принимая во внимание выражение (32), имеем

(33)

${{R}_{w}}_{{{\text{R}}w{\text{I}}}} = 2{{N}_{0}}{{R}_{{xxs}}} = 2{{N}_{0}}Е\cos ( - \pi {\text{/}}2) = 0.$

Отсюда следует, что w_R и w_I являются ортогональными и некоррелированы.

Модульное значение комплексного коэффициента корреляции формируется путем выполнения операций линейной и нелинейной обработки случайных величин, распределенных по нормальному закону (23), (24). При этом плотность вероятностей приобретает вид в соответствии с обобщенным законом Релея [16]

(34)

$p(\rho ) = (\rho {\text{/}}{{\sigma }^{2}})\exp \{ - ({{\rho }^{2}} + {{m}^{2}}){\text{/}}2{{\sigma }^{2}}\} {{I}_{0}}(m\rho {\text{/}}{{\sigma }^{2}}),$

где I₀(·) – функция Бесселя первого рода нулевого порядка; m = ${\text{sqrt}}\left( {m_{{w{\text{R}}}}^{2} + m_{{w{\text{I}}}}^{2}} \right).$

ВЛИЯНИЕ ПРОСТРАНСТВЕННОЙ КОГЕРЕНТНОСТИ СИГНАЛОВ ТОКОВ И НАПРЯЖЕНИЙ НА ТОЧНОСТЬ ДВУХСТОРОННЕГО ОМП ЛЭП

Быстрое определение места повреждения на ЛЭП 110–220 кВ является важной задачей эксплуатационно-ремонтного персонала электросетевых компаний. В зависимости от количества ЛЭП и их технического состояния число повреждений может составлять до несколько десятков и даже сотен в год, для устранения которых требуется привлечение значительных материальных и людских ресурсов [19–21]. От точности ОМП ЛЭП во многом зависит общее время проведения аварийно-восстановительных работ. Широкое применение получили устройства ОМП ЛЭП, использующие методы расчета, основанные на параметрах аварийного режима (измеренных в процессе повреждения токах и напряжениях отдельных фаз и их составляющих) [22, 23]. В устройствах ОМП ЛЭП различных производителей реализуются различные алгоритмы расчета расстояния до места повреждения.

Рассмотрим пример двухстороннего ОМП ЛЭП (рис. 1), не требующего для функционирования синхронизированных векторных изменений [24].

Расчет расстояния до места повреждения производится на основе измерений модулей токов и напряжений по концам ЛЭП I ', I '', U ', U '' и соотношений

(35)

$I{\kern 1pt} 'n{{z}_{{\text{л}}}} + U{\kern 1pt} ' = U{\text{к}},\,\,\,I{\kern 1pt} ''(1 - n){{z}_{{\text{л}}}} + U{\kern 1pt} '' = U{\text{к}}.$

Учитывая, что расстояние до места повреждения (точка К) равно lк = nL, и приравнивая между собой соотношения (35), приходим к выражению

(36)

$lк = [U{\kern 1pt} '' - U{\kern 1pt} ' + I{\kern 1pt} ''L{{z}_{{\text{л}}}}\left] {{\kern 1pt} /{\kern 1pt} } \right[\left( {I{\kern 1pt} '\, + I''} \right){{z}_{{\text{л}}}}],$

где L – длина ЛЭП.

Выражение (36) справедливо для составляющих как обратной, так и нулевой последовательностей.

Рассмотрим пример с повреждением ЛЭП 220 кВ с L = 120 км. Расчет по выражению (36) выполним по составляющим нулевой последовательности, причем z_л = z₀ = = 3 × 0.426 = 1.278 Ом/км. Зафиксированные значения амплитуд токов и напряжений составили: I ' = 2.0 кА, I '' = 0.56 кА, U ' = 40 кВ, U '' = 28 кВ. Получим расстояние до места повреждения на ЛЭП

(37)

$\begin{gathered} ~lк = [U{\kern 1pt} ''\, - U{\kern 1pt} '\, + I{\kern 1pt} ''L{{z}_{{\text{л}}}}\left] {{\kern 1pt} /{\kern 1pt} } \right[(I{\kern 1pt} '\, + I{\kern 1pt} ''){{z}_{{\text{л}}}}]{\text{ = }} \\ = \left[ {28 - 40 + 0.56 \times 120 \times 1.278} \right]{\kern 1pt} /{\kern 1pt} \left[ {\left( {2.0 + 0.56} \right) \times 1.278} \right] = 22.582{\text{ км}}. \\ \end{gathered} $

Выполним оценку влияния пространственной когерентности на точность двухстороннего ОМП ЛЭП. Последовательно аналитически зададим выражения для токов и напряжений в сочетании с воздействием следующих искажающих факторов:

− аддитивные компоненты токов и напряжений в виде интергармоник различных интенсивностей и спектральных диапазонов;

− составляющая в виде белого шума в анализируемом спектре частот.

Точность цифровой обработки сигналов ОМП ЛЭП следует оценивать с помощью модульного значения дискретного коэффициента корреляции, характеризующего нарушения синусоидальности сигналов (выражение (17)). Если два сигнала тока (или напряжения) непосредственно связаны между собой линейно, то степень их когерентности близка к своему максимальному значению равному единице. Для оценки принимаем, что пара случайных сигналов абсолютно когерентные, если модульное значение коэффициента корреляции |ρ| = 1, и абсолютно некогерентные, если |ρ| = 0 [25].

Применительно к задаче ОМП ЛЭП задавались следующие условия анализа сигналов:

− сопоставление сигналов на предмет оценки их пространственной когерентности осуществляется по концам ЛЭП (рис. 1);

− считается, что ток I ' и напряжение U ' являются неискаженными синусоидальными сигналами промышленной частоты f = 50 Гц;

− нарушения синусоидальности характерно для тока I '' и напряжения U '', частота которых также равна f = 50 Гц;

− при моделировании токов и напряжений I ', I '', U ', U '' не учитываются их фазовые соотношения, поскольку в выражении (36) участвуют только их модульные значения;

− исследуются отклонения расчетной точки повреждения, вызванные нарушениями синусоидальности сигналов I '', U '' (выражение (36)), и оценивается соответствующая ошибка ОМП ЛЭП.

Для тока I ' и напряжения U ', относительно которых реализуется расчет коэффициента корреляции, примем синусоидальную модель сигнала в виде

(38)

$x(n) = \left| Х \right|\cos (2\pi {{f}_{0}}n{{T}_{{\text{д}}}} + \varphi )$

с временными последовательностям дискретных отсчетов сигнала.

При формировании дискретных значений тока i'(n) и напряжения u'(n) примем следующие параметры I ' = 1А; U ' = 100 В; f₀ = 50 Гц; Т_д = 1/(f₀N) c; N = 80; φ = 0 рад.

ИССЛЕДОВАНИЯ ВЛИЯНИЯ ИНТЕРГАРМОНИК И ШУМОВ НА ОШИБКИ ОМП ЛЭП ПРИ НАРУШЕНИЯХ ПРОСТРАНСТВЕННОЙ КОГЕРЕНТНОСТИ СИГНАЛОВ ТОКА И НАПРЯЖЕНИЯ

Для искаженных тока I '' и напряжения U '' примем аддитивную модель вида

(39)

$~x(n) = \left| Х \right|\cos (2\pi {{f}_{0}}n{{T}_{{\text{д}}}} + \varphi ) + \mathop \sum \limits_{j = 1}^M \left| {{{Х}_{j}}} \right|\cos (2\pi {{f}_{j}}n{{T}_{{\text{д}}}} + {{\varphi }_{j}}),$

где М – число интергармоник в спектре синусоидального сигнала тока I '' или напряжения U ''; |Х_j|, f_j, φ_j – амплитуда, частота и фаза j-ой интергармонической составляющей.

С целью простоты моделирования и анализа результатов выберем, что ток I '' и напряжение U '' искажены тремя интергармониками (М = 3, выражение (39)) на частотах f₁ = 75 Гц; f₂ = 125 Гц; f₃ = 175 Гц. При этом исследуем влияние соотношений между амплитудами |Х_j| и фазами φ_j интергармоник на коэффициент корреляции сигналов и соответствующие ошибки двухстороннего ОМП ЛЭП.

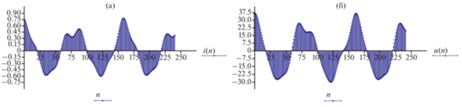
Пусть для амплитуд и фаз интергармоник, входящих в дискретные значения тока i'(n) и напряжения u'(n), имеется следующее соотношение: |Хi₁| = 0.15I''; |Хi₂| = 0.1I ''; |Хi₃| = 0.15I ''; |Хu₁| = 0.1U ''; |Хu₂| = 0.15U ''; |Хu₃| = 0.1U ''; φ_i1 = 0 рад; φ_i2 = (π/6) рад; φ_i3 = = (π/4) рад; φ_u1 = (–π/6) рад; φ_u2 = (–π/4) рад; φ_u3 = 0 рад. Осциллограммы тока и напряжения, соответствующие заданным амплитудно-фазовым соотношениям синусоидальных сигналов тока i '(n) и напряжения u'(n), представлены на (рис. 2). Моделирование выполнено в программном комплексе Mathcad.

Рис. 2.

Синусоидальные сигналы, искаженные интергармониками: (а) тока; (б) напряжения.

Оценку амплитуд тока I '' и напряжения U '' выполним с применением имитации процесса фильтрации измерительным органом устройства ОМП ЛЭП, выполнив дискретное преобразование Фурье (ДПФ) для искаженных сигналов промышленной частоты (рис. 2.)

(40)

$\begin{gathered} {\mathbf{Si}} = (2{\text{/}}N)~\mathop \sum \limits_{n = 0}^{N - 1} I{\kern 1pt} ''[\cos (2\pi {{f}_{0}}n{{Т}_{{\text{д}}}}) + 0.15\cos (2\pi {{f}_{1}}n{{Т}_{{\text{д}}}} + {{\varphi }_{i}}_{1}) + 0.1\cos (2\pi {{f}_{2}}n{{Т}_{{\text{д}}}} + {{\varphi }_{i}}_{2}) + \\ + \,\,0.15\cos (2\pi {{f}_{3}}n{{Т}_{{\text{д}}}} + {{\varphi }_{i}}_{3})]\exp \{ - j \times 2\pi n{\text{/}}N\} = (2{\text{/}}N)~\mathop \sum \limits_{n = 0}^{N - 1} 0.56 \times {{10}^{3}}[\cos (2\pi {{f}_{0}}n{{Т}_{{\text{д}}}}) + \\ + \,\,0.15\cos (2\pi {{f}_{1}}n{{Т}_{{\text{д}}}}\, + \,0)\, + \,0.1\cos (2\pi {{f}_{2}}n{{Т}_{{\text{д}}}}\, + \,\pi {\text{/}}6)\, + \,0.15\cos (2\pi {{f}_{3}}n{{Т}_{{\text{д}}}}\, + \,\pi {\text{/}}4)]\exp \{ - j\, \times \,2\pi n{\text{/}}N\} , \\ \end{gathered} $

(41)

$\begin{gathered} {\mathbf{Su}} = (2{\text{/}}N)~\mathop \sum \limits_{n = 0}^{N - 1} ~U{\kern 1pt} ''[\cos (2\pi {{f}_{0}}n{{Т}_{{\text{д}}}}) + 0.1\cos (2\pi {{f}_{1}}n{{Т}_{{\text{д}}}} + {{\varphi }_{u}}_{1}) + 0.15\cos (2\pi {{f}_{2}}n{{Т}_{{\text{д}}}} + {{\varphi }_{i}}_{2}) + \\ + {\text{ }}0.1\cos (2\pi {{f}_{3}}n{{Т}_{{\text{д}}}} + {{\varphi }_{i}}_{3})]\exp \{ - j \times 2\pi n{\text{/}}N\} = (2{\text{/}}N)\mathop \sum \limits_{n = 0}^{N - 1} 28 \times {{10}^{3}}[\cos (2\pi {{f}_{0}}n{{Т}_{{\text{д}}}}){\text{ + }} \\ + {\text{ }}0.1\cos (2\pi {{f}_{1}}n{{Т}_{{\text{д}}}}\, + \,\pi {\text{/}}6)\, + \,0.1\cos (2\pi {{f}_{2}}n{{Т}_{{\text{д}}}} + \pi {\text{/}}4) + 0.15\cos (2\pi {{f}_{3}}n{{Т}_{{\text{д}}}}\, + \,0)]\exp \{ - j \times 2\pi n{\text{/}}N\} . \\ \end{gathered} $

Результаты расчетов по выражениям (40), (41) показывают, что амплитуды измеренной основной гармоники сигналов тока i''(n) и напряжения u''(n) (рис. 2) соответствуют значениям $I_{{\text{м}}}^{'}$ = |Si| = 0.547 кА, а 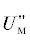|Su| = 30.223 кВ. Таким образом, ДПФ искаженного синусоидального сигнала промышленной частоты не полностью отфильтровало совокупность интергармоник и привело к искажению результатов оценки параметров тока I '' и напряжения U ''. Величина искажений и ошибки оценки амплитуды тока и напряжения зависят от соотношения амплитуд и фаз основной и искажающих интергармоник.

Оценку нарушений пространственной когерентности токов и напряжений выполним с использованием модульного значения коэффициента корреляции (выражение (14)). Используем его нормированную величину, которая в расчетах для совокупностей мгновенных значений токов и напряжений i'(n), i''(n), u'(n), u''(n) примет вид

(42)

$\left| {\rho [х{\kern 1pt} '(n),х{\kern 1pt} ''(n)]} \right| = \left| {{{R}_{х}}_{{'х''}}} \right|{\text{/}}{{[{{R}_{х}}_{{'х'}}{{R}_{х}}_{{''х''}}]}^{{1/2}}},$

где

(43)

$~{{R}_{х}}_{{'х''}} = (1{\text{/}}N)\mathop \sum \limits_{s = 1}^N х{\kern 1pt} '(n)х{\kern 1pt} ''*(n).$

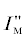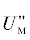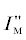С учетом полученных значений и произведем расчет ошибки двухстороннего ОМП ЛЭП в условиях нарушения пространственной когерентности сигналов тока и напряжения. Поставим амплитуды и 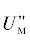в выражение (36) для расчета расстояния до места повреждения на ЛЭП (рис. 1)

(44)

$\begin{gathered} l{\text{мк}} = {\text{ }}[U{\kern 1pt} ''\, - U{\kern 1pt} '\, + I{\kern 1pt} ''L{{z}_{{\text{л}}}}\left] {{\kern 1pt} /{\kern 1pt} } \right[\left( {I{\kern 1pt} '\, + \,I{\kern 1pt} ''} \right){{z}_{{\text{л}}}}] = \\ = \left[ {30.223 - 40 + 0.547 \times 120 \times 1.278} \right]{\kern 1pt} /{\kern 1pt} \left[ {\left( {2.0 + 0.547} \right) \times 1.278} \right] = 22.772{\text{ км}}{\text{.}} \\ \end{gathered} $

Определим ошибку двухстороннего ОМП ЛЭП, вызванную нарушениями пространственной когерентности, по выражению

(45)

$\Delta = l{\text{к}} - l{\text{мк}} = 22.582 - 22.772 = - 0.19{\text{ км}}.$

При рассматриваемом сочетании параметров интергармоник для рассматриваемой ЛЭП с L = 120 км ошибка составила Δ(%) = –0.19 × 100/120 = 0.16%. В табл. 1 приведены результаты имитационного моделирования и расчетов ошибок двухстороннего ОМП при различных амплитудно-фазовых соотношениях интергармоник тока и напряжения.

Таблица 1.

Ошибки ОМП ЛЭП при нарушениях пространственной когерентности сигналов тока и напряжения

Варианты расчетов	Амплитудно-фазовые соотношения интергармоник тока и напряжения												Нормированный коэффициент корреляции тока (напряжения)	Ошибка ОМП ЛЭП (Δ) при нарушении пространственной когерентности
Варианты расчетов	\|Хi₁\|(I '')	\|Хi₂\|(I'')	\|Хi₃\|(I'')	φ_i1	φ_i2	φ_i3	\|Хu₁\| (U'')	\|Хu₂\| (U'')	\|Хu₃\| (U'')	φ_u1	φ_u2	φ_u3	Нормированный коэффициент корреляции тока (напряжения)
1.	0.15	0.1	0.15	0	π/6	π/4	0.1	0.15	0.1	–π/6	–π/4	0	0.973 (0.985)	–0.19 км (0.16%)
2.	0.15	0.15	0.15	π	π	π	0.15	0.15	0.15	– π	– π	– π	0.967 (0.967)	0.176 км (0.15%)
3.	0.15	0.15	0.15	π	π	π	0.15	0.15	0.15	0	0	0	0.967 (0.969)	–0.0165 км (0.014%)
4.	0.15	0.15	0.15	0	0	0	0.15	0.15	0.15	0	0	0	0.969 (0.969)	–0.491 км (0.41%)
5.	0.15	0.15	0.15	π/2	π/2	π/2	0.15	0.15	0.15	0	0	0	0.977 (0.969)	4.063 км (3.39%)
6.	0.15	0.15	0.15	–π/2	–π/2	–π/2	0.15	0.15	0.15	0	0	0	0.989 (0.969)	–4.011 км (3.34%)
7.	0.1	0.1	0.1	–π/2	–π/2	–π/2	0.1	0.1	0.1	0	0	0	0.995 (0.986)	–2.701 км (2.25%)
8.	0.1	0.1	0.1	–π/2	–π/2	–π/2	0.1	0.1	0.1	π/2	π/2	π/2	0.995 (0.991)	–1.567 км (1.31%)
9.	0.1	0.1	0.1	–π/2	–π/2	–π/2	0.1	0.1	0.1	3π/2	3π/2	3π/2	0.995 (0.995)	–3.67 км (3.06%)
10.	0.1	0.1	0.1	–π/2	–π	–3π/2	0.1	0.1	0.1	3π/2	3π/2	3π/2	0.988 (0.995)	–2.21 км (1.84%)

Анализ результатов моделирования и расчетов ошибок двухстороннего ОМП ЛЭП (табл. 1) при различных амплитудно-фазовых соотношениях интергармоник тока и напряжения показал:

− совокупные ошибки ОМП ЛЭП зависят от нарушений синусоидальности сигналов токов и напряжений, амплитудных и фазовых соотношений интергармоник, входящих в состав искаженных сигналов. Амплитудно-фазовые соотношения интергармоник могут приводить как к уменьшению, так и увеличению значений амплитуд тока I'' и напряжения U''. При одинаковых амплитудных соотношениях изменения фазовых соотношений приводят к существенным различиям в ошибках ОМП ЛЭП от 4.063 км до –4.011 км (варианты 5, 6). Уменьшение амплитуд интергармоник в 1.5 раза при тех же фазовых соотношениях приводит к непропорциональному уменьшению ошибки ОМП ЛЭП (варианты 6, 9);

− в измерительных органах цифровых устройств ДПФ обеспечивает полное подавление кратных гармоник, однако при анализе пространственной когерентности дискретных токов и напряжений следует учитывать влияние интергармоник, апериодической составляющей и шумов на процесс цифровой обработки сигналов;

− коэффициент взаимной корреляции может быть выбран в качестве численной характеристики, позволяющей оценить величину искажения сигналов токов и напряжений промышленной частоты, и характеризовать нарушения требований пространственной когерентности. Существует зависимость между нормированным коэффициентом взаимной корреляции и ошибками оценок амплитуд токов и напряжений, поэтому, чем меньше этот коэффициент (существеннее изменение пространственной когерентности синусоидальных сигналов), тем ошибка двухстороннего ОМП ЛЭП будет больше;

− характер влияния нарушений пространственной когерентности на ошибки ОМП ЛЭП зависит от используемого выражения для расчета расстояния до места повреждения ЛЭП. Следовательно, для разных алгоритмов ОМП ЛЭП существует их собственная устойчивость к нарушениям пространственной когерентности;

− учитывая, что нарушения пространственной когерентности оказывают влияние на величину ошибки ОМП, то определение зоны обхода ЛЭП линейными бригадами следует производить на основании результатов моделирования режимов электрической сети и возможных отклонений ПКЭЭ;

− в процессе эксплуатации электрических сетей помимо ошибок, связанных с нарушениями пространственной когерентности сигналов, на точность ОМП ЛЭП оказывают влияние и другие факторы: погрешности измерений трансформаторов тока и напряжения, неточности определения (изменения) удельных параметров ЛЭП, методические ошибки алгоритмов расчета расстояния до места повреждения, электромагнитные помехи и др. Поэтому при организации аварийно-восстановительных работ на ЛЭП следует учитывать аддитивный эффект указанных факторов.

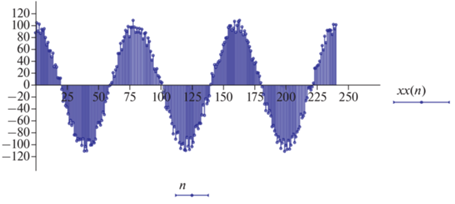
Исследуем влияние шумов на ошибки ОМП ЛЭП при нарушении пространственной когерентности сигналов тока и напряжения. Примем математическую модель сигналов тока и напряжения в виде смеси сигнала x(n) (выражение (38)) и шумовых искажений в анализируемой полосе частот (рис. 3)

(46)

$xx(n) = x(n) + g(n),~~~$

где g(n) – случайные мгновенные значения шумовой составляющей.

Рис. 3.

Осциллограмма синусоидального сигнала тока (напряжения), искаженного шумом.

Результаты моделирования (расчетов) показали, что ДПФ-фильтрация исходного и прореженного сигналов эффективно обеспечивает исключение шумовых составляющих из гармоники промышленной частоты.

Отклонения оценок амплитуд тока I '' и напряжения U '' зависят от интенсивности шума, но составляют не более единиц процентов, что находится в пределах допустимой погрешности измерений.

Так как шумовые составляющие носят случайный характер, имея как положительное, так и отрицательное значение, то при суммировании могут взаимно компенсировать друг друга, поэтому даже в условиях наложения спектров обеспечивается квазикогерентность цифровой обработки сигналов при воздействии широкополосного шума. Расчет нормированного коэффициента взаимной корреляции для сигналов, искаженных и неискаженных шумом, показал, что он близок к единице.

ВЫВОДЫ

Совместную цифровую обработку пространственно-разнесенных сигналов следует производить с учетом пространственной когерентности для минимизации ошибок оценки параметров сигналов токов и напряжений промышленной частоты. Несоблюдение данного требования ведет к существенным ошибкам оценок параметров сигналов.

Для определения степени искажения синусоидальности токов и напряжений по причине нарушений пространственной когерентности целесообразно применять нормированный коэффициент взаимной корреляции.

На примере двухстороннего ОМП ЛЭП показано, что чем меньше коэффициент взаимной корреляции (значительное изменение пространственной когерентности синусоидальных сигналов), тем выше ошибка и ниже точность расчета расстояния до места повреждения.

Характер влияния нарушений пространственной когерентности на ошибки ОМП ЛЭП зависит от используемого выражения для расчета расстояния до места повреждения, поэтому у различных алгоритмов ОМП ЛЭП имеется собственная устойчивость к нарушениям пространственной когерентности.

Определение зоны обхода линейными бригадами на основании данных ОМП ЛЭП следует производить с учетом нарушений пространственной когерентности токов и напряжений. Для этого целесообразно выполнять моделирование режимов электрической сети и возможных отклонений ПКЭЭ от нормативных значений.

Список литературы

Khan Shabbir M.N.S., Liang X. A DFFT and Coherence Analysis-Based Fault Diagnosis Approach for Induction Motors Fed by Variable Frequency Drives // Proceedings of the 2020 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE). 2020. https://doi.org/10.1109/CCECE47787.2020.9255688
Graham M.T., Lediju Bell M.A. Photoacoustic Spatial Coherence Theory and Applications to Coherence-Based Image Contrast and Resolution // Proceedings of the IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 2020. V. 67. Iss. 10. https://doi.org/10.1109/TUFFC.2020.2999343
Hu J.S., Lee M.T. Multi-channel post-filtering based on spatial coherence measure // Signal Processing. 2014. V. 105. P. 338–349.
Li F., Zou L., Songa J., Liang S., Chen Y. Investigation of the spatial coherence function of wind loads on lattice frame structures // J. Wind Engineering and Industrial Aerodynamics. 2021. Vol. 215. 104675.
Есяков С.Я., Лунин К.А., Стенников В.А., Воропай Н.И., Редько И.Я., Баринов В.А. Трансформация электроэнергетических систем // Электроэнергия. Передача и распределение. 2019. № 4(55). С. 134–141.
Воропай Н.И., Ефимов Д.Н., Домышев А.В., Осак А.Б., Панасецкий Д.А. Анализ условий функционирования будущей электроэнергетической системы при рассматриваемом сценарии ее развития // Электроэнергия. Передача и распределение. 2020. № 6(63). С. 34–38.
Ilyushin P.V., Kulikov A.L., Suslov K.V., Filippov S.P. Consideration of Distinguishing Design Features of Gas-Turbine and Gas-Reciprocating Units in Design of Emergency Control Systems. Machines. 2021. Vol. 9. Iss. 3. P. 47.
Phadke A.G., Thorp J.S. Synchronized Phasor Measurements and Their Applications. N.Y.: Springer, 2008. 247 p. https://doi.org/10.1007/978-0-387-76537-2
Kezunovic M., Meliopoulos S., Venkatasubramanian V., Vittal V. Application of Time-Synchronized Measurements in Power System Transmission Networks. N.Y.: Springer, 2014. 176 p. https://doi.org/10.1007/978-3-319-06218-1
Wide area protection & Control technologies, CIGRE Working Group B5.14. 2016.
Synchrophasor Monitoring for Distribution Systems: Technical Foundations and Applications. A White Paper by the NASPI Distribution Task Team NASPI-2018-TR-001, January 2018.
Ribeiro P.F., Duque C.A., Silveira P.M., Cerqueira A.S. Power Systems Signal Processing for Smart Grids. John Wiley & Sons Ltd, 2014. 442 p. https://doi.org/10.1002/9781118639283
Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения. М.: Мир, 1990. 265 с.
William A. Gardner Introduction to Random Processes, With Applications to Signals & Systems. 2nd edition. Mcgraw-Hill, 1990. 496 p.
Shushpanov I., Suslov K., Ilyushin P., Sidorov D. Towards the flexible distribution networks design using the reliability performance metric. Energies. 2021. Vol. 14. Iss. 19. P. 6193.
Радиоэлектронные системы: Основы построения и теория: Справочник / Я.Д. Ширман, С.Т. Багдасарян, А.С. Маляренко и др., под ред. Я.Д. Ширмана. 2-е изд., перераб. и доп. М.: Радиотехника. 2007. 512 с.
Шнеерсон Э.М. Цифровая релейная защита. М.: Энергоатомиздат, 2007. 549 с.
Фальшина В.А., Куликов А.Л. Алгоритмы упрощенной цифровой фильтрации электрических сигналов промышленной частоты // Промышленная энергетика. 2012. № 5. С. 39–46.
Куликов А.Л., Обалин М.Д. Развитие программного обеспечения для поддержки принятия решения при ликвидации повреждения на линиях электропередачи // Известия высших учебных заведений. Электромеханика. 2015. № 2. С. 70–75.
Куликов А.Л., Лукичева И.А. Определение места повреждения линии электропередачи по мгновенным значениям осциллограмм аварийных событий // Вестник Ивановского государственного энергетического университета. 2016. № 5. С. 16–21.
Куликов А.Л., Илюшин П.В., Лоскутов А.А. Повышение быстродействия последовательного анализа в устройствах автоматики энергосистем энергорайонов с распределенной генерацией // Электротехника. 2021. № 2. С. 34–41.
Куликов А.Л., Мисриханов М.Ш. Введение в методы цифровой релейной защиты высоковольтных ЛЭП: Учеб. пособие. М.: Энергоатомиздат, 2007. 197 с.
Обалин М.Д., Куликов А.Л. Применение адаптивных процедур в алгоритмах определения места повреждения ЛЭП // Промышленная энергетика. 2013. № 12. С. 35–39.
Аржанников Е.А., Лукоянов В.Ю., Мисриханов М.Ш. Определение места короткого замыкания на высоковольтных линиях электропередачи / Под ред. В.А. Шуина. М.: Энергоатомиздат, 2003. 272 с.
Кук Ч., Бернфельд М. Радиолокационные сигналы. Пер. с англ. под ред. B.C. Кельзона. М.: Советское радио. 1971. 568 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал