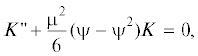1. На главную
  2. Электронные версии
  3. Известия РАН. Энергетика
  4. № 6, 2022

Известия РАН. Энергетика, 2022, № 6, стр. 64-67

Расчет температурного поля в плоском ламинарном потоке жидкости, обогреваемом с одной стороны

Ю. В. Видин 1, Р. В. Казаков 1, *

1 ФГАОУ ВО “Сибирский федеральный университет”
Красноярск, Россия

* E-mail: roman.v.kazakov@gmail.com

Поступила в редакцию 25.01.2022
После доработки 14.06.2022
Принята к публикации 16.06.2022

Полный текст (PDF)

Аннотация

В статье предложен аналитический метод расчета температурного поля в ламинарном потоке жидкости в плоском канале, обогреваемом с одной стороны. Рекомендуемый способ основан на использовании разработанной авторами специальной функции, удовлетворяющей краевым условиям рассматриваемой задачи к исходному дифференциальному уравнению на упорядоченной стадии течения.

Ключевые слова: температурное поле, ламинарный поток, поток жидкости в канале, плоский канал

В статье рассматривается задача о теплообмене при вязкостном течении жидкости в плоском канале, одна стенка которой теплоизолирована, а на противоположной действует граничное условие третьего рода. Подобная проблема была сформулирована в работе [1], некоторые частные числовые результаты которой позднее были приведены в монографии [2]. По нашему мнению, представляет теоретический и практический интерес более детальное математическое изучение сформулированного в [1] процесса, на основании чего может быть существенно расширен данный класс теплофизических задач.

В теоретическом отношении поставленная проблема формулируется следующим образом

(1)
$\frac{{{{\partial }^{2}}\vartheta (\psi ,X)}}{{\partial {{\psi }^{2}}}} = 6(\psi - {{\psi }^{2}})\frac{{\partial (\psi ,X)}}{{\partial X}},$
$0 \leqslant \psi \leqslant 1,\,\,\,\,0 \leqslant x < \infty ,$
(2)
$\frac{{\partial \vartheta }}{{\partial \psi }} = 0\,\,{\text{при}}\,\,\psi = 0,$
(3)
$\frac{{\partial \vartheta }}{{\partial \psi }} = - {\text{Bi}}\vartheta \,\,{\text{при}}\,\,\psi = 1,$
(4)
$\vartheta = 1\,\,{\text{при}}\,\,X = 0.$

Здесь принята безразмерная форма записи уравнения, в которой

$\vartheta = \frac{{{{t}_{c}} - t}}{{{{t}_{c}} - {{t}_{0}}}},\,\,\,\,X = \frac{1}{{{\text{Pe}}}}\frac{x}{\delta },$
$\psi = \frac{y}{\delta },\,\,\,\,{\text{Pe}} = \frac{{\varpi \delta }}{a},$
${\text{Bi}} = \frac{{\alpha \delta }}{\lambda },$
где для определения числа Пекле (Pe) используется усредненная скорость потока жидкости по сечению канала ϖ.

Аналитическое решение задачи, записанной в виде комплекса уравнений (1)–(4), может быть представлено как бесконечный ряд

(5)
$\vartheta (\psi ,X) = \sum\limits_{n = 1}^\infty {{{A}_{n}}{{K}_{n}}(\psi )\exp \left( { - \frac{1}{6}\mu _{n}^{2}X} \right)} ,$
где Kn(ψ) и µnсоответственно собственные функции и собственные значения данной задачи.

Для нахождения Kn(ψ) и µn необходимо решить следующую задачу Штурма-Лиувилля

(6)
(7)
$K{\kern 1pt} ' = 0\,\,{\text{при}}\,\,\psi = 0,$
(8)
$K{\kern 1pt} ' = - {\text{Bi}}K\,\,{\text{при}}\,\,\psi = 1.$

Интеграл дифференциального уравнения (6), относящегося к классу обыкновенных уравнений второго порядка с переменными коэффициентами, не может быть выражен через известные элементарный функции [3]–[7]. В данном конкретном случае, по-видимому, целесообразно использовать специальные функции [8]–[9]. Однако математической особенностью исследуемого процесса является геометрическое несовпадение экстремумов формирующегося в потоке жидкости поля скорости и поля температуры. В тех случаях, когда имеет место их совмещение, успешное математическое решение достигается с помощью применения Конфлюэнтных гипергеометрических функций [3]–[7]. Однако, как показано в монографии [4], применение названных функций приводят в итоге к слишком сложным и весьма громоздким расчетным соотношениям.

В связи с этим в рассматриваемой статье предлагается некоторый особый вид специальной функции, вытекающей из характера дифференциального уравнения (6). В основу рекомендуемого аналитического метода положена оценка максимальной величины собственной функции Kn = 1. Основываясь на этом исходном значении и осуществляя последовательный ряд процедур интегрирования на базе дифференциального уравнения (6) с учетом условия (7), удается получить следующий тип функции

(9)
$\begin{gathered} K(\psi ) = 1 - \frac{{{{\mu }^{2}}}}{6}\left( {{{\psi }^{3}} - \frac{{{{\psi }^{2}}}}{2}} \right) + \frac{{{{\mu }^{4}}}}{6}\left( {\frac{{{{\psi }^{6}}}}{{30}} - \frac{{{{\psi }^{7}}}}{{28}} - \frac{{{{\psi }^{8}}}}{{112}}} \right) \\ - \,\,\frac{{{{\mu }^{6}}}}{6}\left( {\frac{{{{\psi }^{9}}}}{{9 \times 240}} - \frac{{29{{\psi }^{{10}}}}}{{9 \times 14 \times 300}} + \frac{{5{{\psi }^{{11}}}}}{{11 \times 1120}} - \frac{{{{\psi }^{{12}}}}}{{11 \times 12 \times 112}}} \right) + \\ + \,\,\frac{{{{\mu }^{8}}}}{6}\left( {\frac{{{{\psi }^{{12}}}}}{{9 \times 11 \times 12 \times 240}} - \frac{{31{{\psi }^{{13}}}}}{{9 \times 12 \times 13 \times 2800}}} \right. + \frac{{1951{{\psi }^{{14}}}}}{{13 \times 14 \times 44 \times 135 \times 280}} - \\ - \,\,\frac{{{{\psi }^{{15}}}}}{{6 \times 14 \times 15 \times 16 \times 22}} + \left. {\frac{{{{\psi }^{{16}}}}}{{11 \times 12 \times 15 \times 16 \times 112}}} \right). \\ \end{gathered} $

Естественно, используя полином (9), можно и дальше его расширить. Однако для проведения инженерных практических расчетных операций, как правило, вполне достаточным является решение (9).

Подставляя зависимость (9) в граничное условие (8), получим характеристическое уравнение вида

(10)
$\begin{gathered} {{\mu }^{2}}(1 - 0.02142857{{\mu }^{2}} + 0.000147306{{\mu }^{4}} - 0.000000496{{\mu }^{6}}) = \\ = {\text{Bi}}\left( {6 - \frac{{{{\mu }^{2}}}}{2} + 0.0065476{{\mu }^{4}} - 0.000034{{\mu }^{6}} + 0.000000094{{\mu }^{8}}} \right). \\ \end{gathered} $

Из соотношения (10) следует, что при Bi → ∞ (что соответствует граничному условию первого рода) оно упрощается

(11)
$6 - \frac{{{{\mu }^{2}}}}{2} + 0.0065476{{\mu }^{4}} - 0.000034{{\mu }^{6}} + 0.000000094{{\mu }^{8}} = 0.$

По приведенным в монографии [2] данным значение первого собственного числа при Bi → ∞ равно µ1 = 3.818667. Аналогичную величину можно определить на основе алгебраического уравнения (11).

Таким образом уравнение (10) дает возможность рассчитать первое собственное число µ1 с высокой точностью при любой величине Bi. Следует отметить, что при умеренных значения Bi зависимость (10) может быть сведена к биквадратному алгебраическому уравнению, и тогда для нахождения $\mu _{1}^{2}$ удается составить сравнительно простое замкнутое расчетное решение

(12)
$\mu _{1}^{2} = \frac{{{\text{Bi}} + 2}}{{4(0.02142857 + 0.0065476{\text{Bi}})}}\left( {1 - \sqrt {1 - \frac{{96{\text{Bi}}(0.02142857 + 0.0065476{\text{Bi}})}}{{{{{({\text{Bi}} + 2)}}^{2}}}}} } \right).$

В этом случае, когда безразмерное число Bi = 0, характеристическое уравнение также упрощается

(13)
${{\mu }^{2}}(1 - 0.02142857{{\mu }^{2}} + 0.000147306{{\mu }^{4}} - 0.000000496{{\mu }^{6}}) = 0,$
и тогда нахождение на его основе второго корня µ2 сводится к решению кубического алгебраического уравнения, которое нетрудно получить µ2 = 8.751.

В табл. 1 приведены значения первого собственного числа µ1 в зависимости от величины Bi. При составлении таблицы были применены расчетные выражения (10)–(12).

Таблица 1.  

Значения первого собственного числа µ1 характеристического уравнения (10)

Bi µ1 Bi µ1
0 0 2.0 2.5991
0.1 0.7606 5.0 3.1691
0.2 1.0567 10.0 3.4536
0.3 1.2722 20.0 3.6242
0.4 1.4447 50.0 3.7378
0.5 1.5886 100.0 3.7777
1.0 2.0837 ∞ 3.8187

Для определения коэффициентов An ряда (5) нужно использовать условие (4), которое описывает распределение температуры по сечению потока жидкости на входе в канал (X = 0). Исходя из него, вычисление коэффициентов An осуществляется с помощью выражения

(13)
$\sum\limits_{n = 1}^\infty {{{A}_{n}}{{K}_{n}}(\psi ) = 1} .$

Отсюда получим [5]

(14)
${{A}_{n}} = \frac{{\int\limits_0^1 {(\psi - {{\psi }^{2}}){{K}_{n}}d\psi } }}{{\int\limits_0^1 {(\psi - {{\psi }^{2}})K_{n}^{2}d\psi } }},$
где собственные функции Kn описываются формулами родственными (9).

В заключение нужно отметить, что при проведении технических расчетов особо важными являются величины µ1 и K1(ψ). Это обусловлено тем, что бесконечный ряд в решении (5) оказывается быстросходящимся. Начиная со сравнительно небольших значений осевой координаты X (обычно при X ≥ 0.03), все слагаемые в формуле (5) становятся пренебрежимо малыми по сравнению с первым числом ряда.

Список литературы

  1. Schenk I. A problem of heat transfer in laminar flow between parallel plates, Appe. Scient Res., 1955, A5, N. 2–3, p. 241–244.

  2. Петухов Б.С. Теплообмен и сопротивление при ламинарном течении жидкости в трубах. М.: Энергия, 1967. С. 411.

  3. Видин Ю.В., Иванов В.В., Медведев Г.Г. Расчет теплообмена при ламинарном течении жидкости в каналах. Красноярск, КрПИ, 1971. С. 144.

  4. Видин Ю.В., Иванов В.В., Казаков Р.В. Инженерные методы расчета задач теплообмена. Красноярск, СФУ, 2014. С. 164.

  5. Видин Ю.В., Казаков Р.В. Расчет теплообмена при ламинарном течении жидкости в цилиндрическом канале при наличии аксиальной теплопроводности. Теплофизика высоких температур. 2019. Т. 57. № 2. С. 308–311.

  6. Маделунг Э. Математический аппарат физики. М.: Наука, 1968. С. 618.

  7. Абрамовиц М., Стиган Л. Справочник по специальным функциям. М.: Наука, 1979. С. 830.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Энергетика

Архивы выпусков Информация о журнале Отправить рукопись в журнал