Известия РАН. Энергетика, 2023, № 1, стр. 72-78

В статье рассмотрены расчетные рекомендации для сил взаимодействия между соленоидом и соосным витком в двух модификациях: с использованием полных эллиптических интегралов первого и второго рода и функции Лежандра второго рода с полуцелым индексом. Вместе с тем выражение для силы взаимодействия двух соосных круговых контуров радиусов ${{R}_{1}}$ и ${{R}_{2}}$ с токами ${{i}_{1}}$ и ${{i}_{2}}$, данные в [5] и перезаписанные в виде

где $g = \frac{{{{z}^{2}} + {{R}_{1}}^{2} + {{R}_{2}}^{2}}}{{2{{R}_{1}}{{R}_{2}}}},$ с расстоянием $z$ между параллельными плоскостями расположения контуров, и в варианте (П2.-3) в [5] в виде: дают основание утверждать, что присоединенная функция Лежандра второго рода с полуцелым индексом ${{Q}_{{1/2}}}^{1}\left( g \right)$ с $g = \frac{{2 - {{k}^{2}}}}{{{{k}^{2}}}}$ и с ${{k}^{2}} = \frac{{4{{R}_{1}}{{R}_{2}}}}{{{{z}^{2}} + {{{\left( {{{R}_{1}} + {{R}_{2}}} \right)}}^{2}}}}$, равна что и было продемонстрировано в [5].

Для случая, когда ${{R}_{1}} = {{R}_{2}} = R$ и $z = R,$ $g = 1.5$ и ${{k}^{2}} = 0.8$, имеем

Численное значение для $Q_{{1/2}}^{1}\left( {1.5} \right) \cong - {\kern 1pt} 0.639$ можно проверить по формуле (3), подставляя ${{k}^{2}} = 0.8$, и тогда, определяя $K$ и $E$ для этого значения, будем иметь:

Выражение (3) проверялось численно на примере, когда в одном из вариантов ${{k}^{2}} = 0.25,\,\,\left( {k = 0.5} \right)$. В этом случае $g = 7.0$ и $Q_{{1/2}}^{1}\left( 7 \right) = - 0.0455$. Для правой стороны (3) независимое вычисление через полные эллиптические интегралы дает такое же численное значение.

В работе [5] формула (11) было записано выражение для коэффициента взаимной индукции двух круговых соосных контуров с принятыми там обозначениями в виде:

где $x$ – расстояние между плоскостями расположения контуров с радиусами ${{R}_{1}}$ и ${{R}_{2}}$, и тогда

${{k}^{2}} = \frac{{4{{R}_{1}}{{R}_{2}}}}{{{{{\left( {{{R}_{1}} + {{R}_{2}}} \right)}}^{2}} + {{x}^{2}}}}.$ Вместе с тем в формуле (2) в [5] выражение для ${{k}^{2}}$ записано с опечаткой как ${{k}^{2}} = \frac{{4{{R}_{1}}{{R}^{2}}}}{{{{{\left( {{{R}_{1}} + {{R}_{2}}} \right)}}^{2}}}} + {{x}^{2}}.$

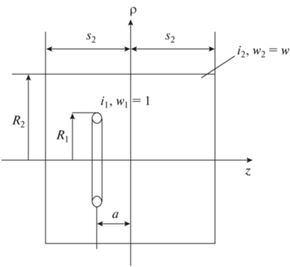
Далее произведем сопоставление выражений для сил взаимодействия между соосными соленоидами длиной $2{{s}_{1}}$ и радиусом ${{R}_{1}}$ с круговым витком ${{R}_{2}}$, принимая за основу рис. 1 в [6] при $a = 0$ и ${{s}_{2}} \to 0$, который здесь воспроизведен также на рис. 1.

Выражение для силы взаимодействия между соленоидом и витком с токами 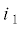и ${{i}_{2}}$ по оси $z$ (рис. 1) известно и представлено формулой (29) в [6], которая при $a = 0$ и ${{s}_{1}} = s$ может быть записана в виде:

где

Здесь ${{Q}_{{1/2}}}\left( {{{g}_{{1,2}}}} \right)$ – функции Лежандра второго рода, которые могут быть представлены через полные эллиптические интегралы первого и второго рода в виде [1]:

Учитывая, что [5]

подстановкой (9) в (8) и далее в (6) в результате получим:

Результат (10) можно перезаписать в следующем виде:

Полагая в формуле (6) ${{R}_{2}} = 0.5{{R}_{1}}$ и $s = {{R}_{1}}$, найдем по формуле (6) при $z = s$, с учетом табличных значений [7] для ${{Q}_{{1/2}}}$:

Полагая в (9) $k_{1}^{2} = 0.888$ и $k_{2}^{2} = 0.32$ и осуществляя вычисления по формуле (11) с учетом таблиц для $K$ и $E$ от ${{k}^{2}}$, найдем:

т.е. практически то же значение, что и по предыдущему расчету.

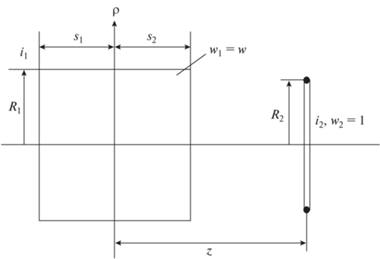
При расположении витка внутри соосного соленоида как на рис. 2, можно воспользоваться следующим рядом для силы взаимодействия [6]:

где $q_{{11}}^{{}} = \left( { - {{s}_{2}} + a} \right){\text{/}}{{R}_{2}},\,\,q_{{12}}^{{}} = \left( { - {{s}_{2}} - a} \right){\text{/}}{{R}_{2}},$ который при $a = 0$ обращается в ноль.

При расположении витка с противоположной стороны плоскости с $\rho $ (рис. 2) значение силы следует изменить на противоположное.

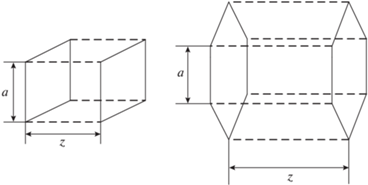
Витки, расположенные в параллельных плоскостях и формирующие соленоиды, могут быть и другой формы. Здесь будут рассмотрены витки в форме квадрата $\left( {n = 4} \right)$ и шестиугольника $\left( {n = 6} \right)$. Оценку силовых взаимодействий между этими витками осуществим, используя выражения для взаимной индуктивности (4.47) и (4.48), приведенные в [2].

При $n = 4.6$ и близко расположенных многоугольниках запишем для $M$ $\left( {n = 4} \right)$ и $\left( {n = 6} \right)$ выражения (4–47) и (4–48), данные в [2]:

и при $z = 0.5a$ имеем для (15) – ${{\mu }_{0}}0.6986$.

Действуя аналогично для $n = 6$, получим:

и при $z = 0.5a$ имеем:

Умножая (15) и (16) на произведение токов ${{i}_{1}}{{i}_{2}}$ в витках, найдем и силу взаимодействия для случая $n = 4$:

и аналогичную формулу для $n = 6$

Теперь исходим из предпосылки, что площади, охватываемые квадратными и круговыми витками, равны, т.е., что ${{a}^{2}} = \pi {{R}^{2}}$ и $R = \frac{a}{{\sqrt \pi }} = 0.5642a$. Тогда при $z = 0.5a$ значение для силы взаимодействия равно: ${{f}_{z}}\left| {_{{n = 4}}} \right. \cong - {{\mu }_{0}}{{i}_{1}}{{i}_{2}}0.6986$.

Теперь определяем ${{k}^{2}}$:

и тогда по формуле (2) получим:

Для выяснения возможности оценки силы взаимодействия через эквивалентный по площади правильный шестиугольник со стороной $a$ заметим, что площадь, охватываемая таким шестиугольником равна:

Эквивалентные по площади круговой контур определяется из равенства:

Теперь можно сопоставить результаты вычислений по формул (19) и (2), приняв $z = 0.5a$. Подставив в формулу (19) принятые условия имеем

Находим теперь $\frac{z}{R} = \frac{{0.5}}{{0.9094}} \cong 0.55$ и ${{k}^{2}} = \frac{{4{{R}^{2}}}}{{{{z}^{2}} + 4{{R}^{2}}}} \cong 0.93.$

Тогда получим в согласии с таблицей из приложения 4 в [2]

против $ - {{\mu }_{0}}{{i}_{1}}{{i}_{2}}1.446,$ и результаты расчетов практически одинаковы.

Близость значений для силы $f$ дает основание утверждать, что и при условии равенства площадей, охватываемых квадратными и шестиугольными контурами, электродинамическую силу можно оценивать по формулам (18) и (19), не прибегая к нахождению полных эллиптических интегралов первого и второго рода.