1. На главную
  2. Электронные версии
  3. Известия РАН. Серия биологическая
  4. № 4, 2020

Известия РАН. Серия биологическая, 2020, № 4, стр. 393-400

Биоритмы роста европейской жемчужницы Margaritifera margaritifera (Bivalvia, Margaritiferidae). Популяция реки Варзуга (Мурманская область)

А. А. Зотин *

Институт биологии развития им. Н.К. Кольцова РАН
119334 Москва, ул. Вавилова, 26, Россия

* E-mail: zotin@idbras.ru

Поступила в редакцию 26.06.2019
После доработки 23.09.2019
Принята к публикации 21.10.2019

Полный текст (PDF)

Аннотация

Проведено исследование индивидуального линейного роста 90 особей пресноводной жемчужницы Margaritifera margaritifera путем измерения последовательных годовых колец на поверхности раковины. Установлено, что рост каждого моллюска может быть описан с помощью единого уравнения, частный случай которого – уравнение Берталанфи со средним коэффициентом замедления роста a = 0.048 год–1 и коэффициентом начальных условий d = 5.3 мм/год. Отмечено, что рост моллюсков сопровождается тремя закономерными биоритмами с периодами 13.4, 6.8 и 4.0 года, причем два первых биоритма затухающие, последний имеет постоянную амплитуду. Обнаружено, что уменьшение амплитуды затухающих биоритмов может быть описано степенны́м уравнением с одинаковыми коэффициентами. Обсуждены вопросы, связанные с природой выявленных биоритмов.

Живые организмы с точки зрения термодинамики нелинейных процессов – неравновесные диссипативные структуры (Prigogine, Nicolis, 1971; Nicolis, 1972; Васильев, 1976; Зотин А.И., 1976; Лампрехт, 1976; Рубин, 1976; Nicolis, Prigogine, 1977; Haken, 1978; Зотин А.А., 2012). В таких структурах любой процесс, сопровождаемый избыточной диссипацией энергии, характеризуется ритмами, каждый из которых связан с определенным стационарным состоянием (Prigogine, 1972; Малек-Мансур и др., 1980).

Один из таких процессов, характеризующих биологические системы – рост организмов. При исследовании роста выявляются 1–3 биоритма в зависимости от характерного времени процесса (Зотин А.А., 2009; Зотин А.А., Клейменов, 2013). Так, при ежесуточных измерениях у многих видов животных выявлены биоритмы роста с периодом ∼2 нед (Сипачев, 1970). Для промежутков времени, сопоставимых с продолжительностью жизни, описаны два эндогенных биоритма удельной скорости роста, один из которых связан с текущим стационарным состоянием живой системы, другой – с конечным стационарным состоянием, к которому организм стремится на протяжении всей жизни (Зотин А.И., 1974; Зотин А.И., Зотина, 1993; Zotin A.A., Zotin A.I., 1996, 1997).

Выявление биоритмов роста связано с определенными трудностями, в частности с необходимостью изучения большого периода онтогенеза с частотой измерений, позволяющей надежно выявлять биоритм (период между измерениями должен быть по крайней мере в 3 раза меньше периода биоритма). Один из видов, с помощью которого можно получить данные, позволяющие обнаружить и охарактеризовать биоритмы роста, – пресноводный двустворчатый моллюск Margaritifera margaritifera. Представители этого вида часто живут >100 лет, а наличие годовых колец на поверхности раковины дает возможность исследовать рост с частотой измерений 1 раз в год.

Цель работы – выявление биоритмов удельной скорости роста и определение параметров индивидуального линейного роста в популяции M. margaritifera, обитающей в р. Варзуга.

МАТЕРИАЛЫ И МЕТОДЫ

Створки раковин вынесенных на берег в результате весеннего половодья погибших двустворчатых моллюсков пресноводная жемчужница M. margaritifera L. собирали на правом берегу р. Варзуга (Терский р-н Мурманской обл.) сразу после впадения в нее р. Пана. Всего исследовали раковины 90 моллюсков. Верхний конхиолиновый слой удаляли путем кипячения створок в 1 М растворе KOH в течение 10 мин. В результате годовые кольца роста, образованные средним призматическим слоем, стали отчетливо видны. Изображения раковин получали путем их сканирования на сканере HP ScanJet 5400c (Китай). Длину каждого неповрежденного годового кольца измеряли с помощью программы Excel с точностью 0.1 мм по следующей схеме:

в лист книги Excel внедряли рисунок (вкладка “вставка”–“рисунок”);

изменяли размер рисунка и его резкость так, чтобы годовые кольца были отчетливо видны (кликнуть правой кнопкой мыши по рисунку, выбрать опции “формат рисунка”–“размер” и “формат рисунка”–“настройка рисунка”);

внедряли стрелку (вкладка “вставка”–“фигуры”), концы которой располагали на передней и задней оконечностях измеряемого годового кольца (рис. 1);

Рис. 1.

Определение длины годового кольца с использованием программы Excel.

определяли опции стрелки “высота фигуры” и “ширина фигуры” (вкладка “формат”, окна справа) и рассчитывали длину стрелки (годового кольца) по теореме Пифагора.

Использовали единое уравнение роста, частный случай которого – уравнение Берталанфи (Zotin, 2015):

(1)
${{{\text{d}}{{L}_{t}}} \mathord{\left/ {\vphantom {{{\text{d}}{{L}_{t}}} {{{L}_{t}}{\text{d}}t}}} \right. \kern-0em} {{{L}_{t}}{\text{d}}t}} = {{V}_{0}}{{\left( {1 - a} \right)}^{t}},$
где Lt – длина годового кольца в возрасте t; V0 – начальная скорость роста; a – коэффициент, определяющий замедление роста.

Данные аппроксимировали рекуррентной формой уравнения (1):

(2)
$\Delta L = - a{{L}_{t}} + d,\,\,\,\,d = {{ - {{V}_{0}}} \mathord{\left/ {\vphantom {{ - {{V}_{0}}} {\ln \left( {1 - a} \right)}}} \right. \kern-0em} {\ln \left( {1 - a} \right)}} + {{L}_{0}},$
где ΔL – прирост длины раковины за год, следующий за возрастом t; L0 – размер раковины в возрасте t = 0.

Сравнение коэффициентов уравнения (2) проводили методом регрессионного анализа. Пригодность использования этого уравнения оценивали с помощью критерия нелинейности (Зотин А.А., 2000).

Возраст моллюска (T) вычисляли, суммируя возраст первого измеренного годового кольца (T1) и число распознаваемых годовых колец на поверхности раковины. Возраст первого измеренного годового кольца рассчитывали с помощью аналитической формы уравнения (1):

${{T}_{1}} = {{\log }_{{(1--a)}}}(1 - {{a{{L}_{1}}} \mathord{\left/ {\vphantom {{a{{L}_{1}}} d}} \right. \kern-0em} d}),$
где L1 – длина первого измеренного годового кольца. Необходимость такого способа определения возраста связана с тем, что почти у всех моллюсков примакушечная зона раковины корродирована и часть годовых колец не детектируется.

Полученные данные сглаживали кубическими сплайнами и строили временнóй ряд зависимости относительной скорости роста (dL/Ldt) от возраста годового кольца с использованием программы Matlab (версия 7.3.0.267, которая была разработана компанией The MathWorks, Inc., США).

Основной тренд и биоритмы определяли методом сингулярного спектрального анализа с помощью программы “Гусеница” (версия 3.40, которая была разработана компанией GistaT Group, Россия). При применении программы была выбрана опция “без центрирования”. Выбор опции “длина гусеницы” (“длина окна”) осуществляли следующим образом: если число измеренных годовых колец не превышало 24, то использовали длину окна, равную округленной до целого числа половины измеренных колец. В противном случае использовали длину окна 12. Ритмы с периодом <3 лет считали “стохастическим шумом”. Период биоритмов (P) определяли, вычисляя среднее значение удвоенных промежутков времени между последовательными локальными экстремумами. Амплитуду биоритмов (A) вычисляли как половину разницы между значениями последовательных локальных экстремумов.

Зависимость амплитуды колебаний от возраста для затухающих биоритмов аппроксимировали степенным уравнением

(3)
$A = b{{T}^{c}},$
где A – амплитуда; T – возраст достижения экстремума; b, c – коэффициенты.

Аппроксимацию уравнениями (1)–(3) проводили с использованием программы Matlab (версия 7.3.0.267).

Сравнение периодов биоритмов в онтогенезе отдельных моллюсков и средних значений периодов у разных особей проводили методом дисперсионного анализа (ANOVA). Статистические распределения, составленные из средних значений параметров, рассчитанных для разных моллюсков, сравнивали с нормальным распределением по критерию χ2. Во всех случаях, когда вычисляли средние значения, вычисляли также стандартную ошибку среднего (Ивантер, Коросов, 2010).

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Основная тенденция линейного роста отдельных особей M. margaritifera хорошо описывается уравнением (2). Коэффициенты a этого уравнения, определяющие замедление роста, широко варьируют у разных моллюсков от 0.017 до 0.081 год–1 и достоверно различаются (p < 0.001) (табл. 1). Тем не менее вариационные ряды, составленные из значений коэффициентов уравнения (2) для разных особей, согласно критерию χ2 распределены нормально. Их средние значения (a = 0.048 ± 0.001 год–1, d = 5.3 ± 0.1 мм/год (n = 90, где n – число измерений)) могут быть использованы для характеристики популяции р. Варзуга при межпопуляционных и межвидовых исследованиях.

Таблица 1.  

Индивидуальные размерные, возрастные и ростовые характеристики M. margaritifera

№ особи n L, мм T, год a, год–1 d, мм/год m1 P1, год m2 P2, год m3 P3, год
1 21 92.8 44 0.081 ± 0.007 7.7 ± 0.5 – – 5 7.0 ± 0.6 8 4.3 ± 0.5
2 14 82.7 22 0.079 ± 0.014 7.8 ± 0.9 – – 4 8.0 ± 1.2 5 4.0 ± 0.8
3 20 94.5 35 0.070 ± 0.008 7.2 ± 0.5 – – 6 6.0 ± 0.6 10 3.8 ± 0.2
4 23 75.4 37 0.069 ± 0.008 5.6 ± 0.4 2 18.0 6 7.6 ± 1.6 11 3.8 ± 0.5
5 23 72.8 30 0.069 ± 0.006 5.7 ± 0.4 3 12.0 ± 8.0 6 7.6 ± 1.2 10 4.0 ± 0.5
6 12 89.2 35 0.067 ± 0.016 6.5 ± 0.8 – – 3 8.0 5 4.5 ± 0.5
7 26 84.5 34 0.067 ± 0.007 6.3 ± 0.5 4 14.0 ± 2.0 8 6.9 ± 1.1 12 4.0 ± 0.7
8 12 110.5 43 0.062 ± 0.014 6.6 ± 0.9 – – 3 7.0 ± 1.0 6 3.6 ± 0.4
9 27 97.3 36 0.061 ± 0.005 6.6 ± 0.4 2 16.0 5 6.0 11 3.8 ± 0.6
10 43 98.6 51 0.061 ± 0.004 6.2 ± 0.3 5 20.5 ± 0.5 12 6.9 ± 0.6 22 3.7 ± 0.3
11 23 82.0 32 0.061 ± 0.009 5.8 ± 0.6 – – 6 6.8 ± 0.5 11 3.6 ± 0.4
12 30 98.1 37 0.059 ± 0.006 6.5 ± 0.4 5 10.5 ± 1.0 9 6.0 15 3.6 ± 0.2
13 22 91.1 34 0.059 ± 0.006 6.2 ± 0.4 3 14.0 ± 6.0 6 7.6 ± 1.0 7 4.7 ± 0.7
14 13 77.6 19 0.058 ± 0.022 6.7 ± 1.3 2 12.0 – – 6 4.4 ± 0.4
15 15 91.4 38 0.058 ± 0.019 5.9 ± 1.1 2 12.0 3 7.0 ± 1.0 6 4.4 ± 0.4
16 37 97.5 49 0.058 ± 0.005 5.9 ± 0.4 4 16.0 ± 3.1 10 6.9 ± 0.9 15 4.4 ± 0.4
17 18 88.1 36 0.058 ± 0.013 5.8 ± 0.7 3 10.0 ± 2.0 4 8.0 ± 1.2 5 4.0
18 14 79.2 24 0.057 ± 0.015 5.9 ± 0.9 3 10.0 3 7.0 ± 1.0 6 4.0
19 42 93.4 50 0.056 ± 0.006 5.5 ± 0.4 5 12.5 ± 5.4 10 7.8 ± 0.8 18 4.4 ± 0.3
20 25 86.7 31 0.056 ± 0.007 5.8 ± 0.4 3 13.0 ± 7.0 8 6.0 ± 0.4 12 4.0 ± 0.4
21 33 76.8 43 0.056 ± 0.006 4.7 ± 0.4 6 11.6 ± 1.6 10 6.2 ± 0.6 18 3.5 ± 0.3
22 6 46.5 11 0.056 ± 0.022 5.5 ± 0.7 – – – – 2 4.0
23 6 47.6 12 0.056 ± 0.014 5.4 ± 0.5 – – – – 2 4.0
24 37 98.7 45 0.055 ± 0.004 5.8 ± 0.3 6 12.8 ± 1.0 9 7.0 ± 0.7 16 4.0 ± 0.3
25 12 93.3 30 0.055 ± 0.015 6.3 ± 1.0 3 10.0 ± 2.0 3 7.0 ± 1.0 4 4.0
26 35 101.8 46 0.055 ± 0.004 6.0 ± 0.3 6 12.0 ± 0.6 11 5.8 ± 0.4 17 3.9 ± 0.2
27 19 89.9 28 0.055 ± 0.006 6.2 ± 0.4 2 18.0 5 7.0 ± 0.6 7 4.3 ± 0.3
28 27 84.2 34 0.054 ± 0.009 5.4 ± 0.5 3 16.0 8 6.3 ± 0.3 12 4.2 ± 0.5
29 26 93.6 36 0.054 ± 0.007 5.9 ± 0.5 5 9.0 ± 1.7 8 6.6 ± 0.8 12 3.8 ± 0.4
30 28 86.6 37 0.054 ± 0.006 5.4 ± 0.4 3 20.0 ± 2.0 9 5.8 ± 0.7 13 4.0 ± 0.4
31 11 49.7 16 0.054 ± 0.018 4.7 ± 0.6 – – – – 5 4.0 ± 0.8
32 36 98.9 53 0.053 ± 0.005 5.5 ± 0.4 5 15.5 ± 2.2 9 8.0 ± 0.9 11 4.4 ± 0.3
33 9 86.4 31 0.052 ± 0.019 5.6 ± 0.9 – – – – 3 4.0
34 13 89.4 37 0.052 ± 0.016 5.4 ± 0.9 2 12.0 3 7.0 ± 1.0 6 4.4 ± 0.4
35 35 98.9 50 0.051 ± 0.006 5.4 ± 0.5 4 14.7 ± 2.4 9 8.0 ± 1.4 18 3.8 ± 0.2
36 22 85.3 41 0.051 ± 0.006 4.9 ± 0.3 2 20.0 5 7.0 ± 1.3 10 4.0 ± 0.3
37 33 97.4 43 0.051 ± 0.005 5.5 ± 0.4 5 14.0 ± 0.8 8 8.6 ± 1.6 14 4.5 ± 0.5
38 33 101.0 46 0.051 ± 0.004 5.6 ± 0.3 4 12.7 ± 1.3 10 6.7 ± 0.3 16 4.0 ± 0.3
39 19 79.2 28 0.050 ± 0.008 5.2 ± 0.5 – – 5 6.5 ± 1.0 8 4.3 ± 0.3
40 48 103.9 63 0.050 ± 0.003 5.4 ± 0.3 8 12.3 ± 1.0 12 8.0 ± 1.0 23 4.1 ± 0.4
41 29 95.7 38 0.050 ± 0.006 5.5 ± 0.4 – – 9 6.0 ± 0.8 10 4.0 ± 0.6
42 10 94.6 40 0.050 ± 0.018 5.4 ± 1.1 – – 3 7.0 ± 1.0 3 4.0
43 23 84.9 35 0.049 ± 0.009 5.1 ± 0.6 2 20.0 6 7.6 ± 1.0 12 3.5 ± 0.4
44 29 94.4 37 0.049 ± 0.006 5.5 ± 0.4 – – 8 5.7 ± 1.1 10 4.0 ± 0.3
45 26 93.0 39 0.049 ± 0.007 5.3 ± 0.5 4 10.0 ± 2.0 6 6.0 ± 0.6 10 4.0 ± 0.3
46 40 103.1 57 0.048 ± 0.005 5.3 ± 0.4 7 10.7 ± 1.0 12 6.0 ± 0.7 19 4.0 ± 0.5
47 9 58.1 14 0.048 ± 0.026 5.5 ± 1.0 – – 2 8.0 3 4.0
48 23 89.0 33 0.048 ± 0.007 5.3 ± 0.5 5 10.0 ± 1.8 6 7.2 ± 1.7 12 3.6 ± 0.2
49 18 73.7 25 0.047 ± 0.015 4.9 ± 0.8 2 12.0 6 6.0 8 4.3 ± 0.3
50 14 79.2 26 0.047 ± 0.008 5.2 ± 0.5 2 12.0 3 8.0 4 4.7 ± 0.7
51 18 72.5 26 0.047 ± 0.006 4.8 ± 0.3 – – 6 6.0 8 4.0 ± 0.6
52 11 46.8 15 0.047 ± 0.018 4.3 ± 0.6 – – 2 8.0 5 4.5 ± 0.5
53 11 93.3 35 0.047 ± 0.017 5.4 ± 0.9 – – 3 7.0 ± 1.0 5 3.5 ± 0.5
54 9 50.5 13 0.046 ± 0.015 5.3 ± 0.5 – – 2 8.0 4 4.0 ± 1.2
55 19 75.3 25 0.046 ± 0.012 5.0 ± 0.7 – – 3 8.0 6 4.8 ± 0.5
56 32 87.6 42 0.046 ± 0.007 4.7 ± 0.40 6 10.8 ± 0.5 9 7.5 ± 1.1 9 4.0 ± 0.4
57 11 52.5 26 0.045 ± 0.007 3.4 ± 0.20 – – 3 6.0 ± 2.0 3 4.0
58 20 79.9 28 0.045 ± 0.010 5.0 ± 0.6 4 10.0 ± 1.2 6 6.4 ± 0.7 7 4.3 ± 0.6
59 8 46.4 15 0.045 ± 0.024 4.2 ± 0.7 – – 2 8.0 3 4.0
60 30 85.9 43 0.045 ± 0.003 4.5 ± 0.2 5 12.0 ± 1.4 9 6.5 ± 0.8 15 3.7 ± 0.2
61 26 94.9 34 0.045 ± 0.005 5.4 ± 0.3 5 11.0 ± 3.4 7 7.3 ± 0.7 14 3.7 ± 0.3
62 26 91.4 45 0.044 ± 0.007 4.7 ± 0.5 2 20.0 8 6.3 ± 1.4 11 4.4 ± 0.5
63 55 115.4 72 0.044 ± 0.003 5.3 ± 0.2 9 11.8 ± 0.7 2 6.0 28 3.7 ± 0.2
64 9 81.3 20 0.043 ± 0.015 5.9 ± 0.8 – – 2 8.0 3 4.0
65 36 102.5 45 0.043 ± 0.003 5.1 ± 0.3 6 10.8 ± 1.7 11 5.8 ± 0.6 18 3.6 ± 0.3
66 17 89.5 25 0.043 ± 0.011 5.8 ± 0.7 – – 5 6.0 8 4.3 ± 0.3
67 30 105.0 43 0.042 ± 0.005 5.3 ± 0.4 – – 8 7.7 ± 1.4 12 4.5 ± 0.5
68 32 88.9 43 0.041 ± 0.005 4.4 ± 0.3 7 10.0 ± 1.5 11 5.6 ± 0.5 15 4.3 ± 0.2
69 41 103.9 54 0.040 ± 0.004 4.7 ± 0.3 4 18.7 ± 3.7 11 6.8 ± 0.9 21 3.7 ± 0.2
70 9 85.5 26 0.039 ± 0.017 5.2 ± 0.8 – – 2 6.0 5 3.5 ± 0.5
71 32 89.8 44 0.038 ± 0.004 4.2 ± 0.3 – – 19 5.8 ± 0.4 17 3.6 ± 0.3
72 10 51.5 14 0.038 ± 0.031 4.6 ± 1.0 – – 3 6.0 5 3.5 ± 0.5
73 44 108.2 58 0.037 ± 0.003 4.6 ± 0.2 9 10.5 ± 0.7 14 6.3 ± 0.8 24 3.6 ± 0.2
74 26 87.2 35 0.037 ± 0.005 4.4 ± 0.3 4 13.3 ± 6.4 7 6.7 ± 0.4 11 4.4 ± 0.4
75 9 49.8 14 0.036 ± 0.029 4.6 ± 1.0 – – 2 8.0 2 4.0
76 8 76.3 21 0.035 ± 0.022 5.0 ± 0.7 – – – – 3 4.0
77 38 95.9 56 0.035 ± 0.003 3.9 ± 0.2 4 18.7 ± 1.8 9 8.0 ± 0.8 17 4.5 ± 0.3
78 42 108.4 54 0.035 ± 0.004 4.4 ± 0.3 – – 14 6.0 ± 0.5 23 3.5 ± 0.2
79 9 76.2 23 0.034 ± 0.017 4.7 ± 0.5 – – 2 6.0 5 3.5 ± 0.5
80 24 106.5 36 0.034 ± 0.007 5.0 ± 0.6 – – 7 6.3 ± 0.3 12 4.2 ± 0.6
81 8 40.5 15 0.033 ± 0.072 3.6 ± 2.1 – – 2 6.0 2 4.0
82 9 65.1 18 0.032 ± 0.011 4.7 ± 0.3 – – 2 6.0 5 3.5 ± 0.5
83 36 101.6 52 0.032 ± 0.004 4.0 ± 0.3 – – 11 6.0 ± 0.6 17 4.0 ± 0.2
84 28 93.2 46 0.031 ± 0.005 3.8 ± 0.4 6 10.0 ± 0.9 7 6.7 ± 0.4 17 3.4 ± 0.2
85 33 101.7 56 0.030 ± 0.005 3.8 ± 0.4 – – 9 7.0 ± 0.8 13 4.3 ± 0.2
86 6 49.7 13 0.030 ± 0.022 4.6 ± 0.8 – – 2 6.0 2 4.0
87 18 71.7 26 0.028 ± 0.010 3.9 ± 0.5 – – 5 7.5 ± 1.9 6 4.4 ± 0.4
88 46 119.4 61 0.027 ± 0.003 4.0 ± 0.3 9 13.3 ± 0.4 13 6.3 ± 0.5 22 3.6 ± 0.3
89 18 106.7 30 0.024 ± 0.011 5.0 ± 0.9 3 13.0 ± 5.0 6 6.0 ± 0.6 6 4.0
90 13 71.1 19 0.017 ± 0.016 4.3 ± 0.7 – – 4 6.7 ± 0.7 7 3.7 ± 0.6

Примечание. n – число измеренных годовых колец; L – длина раковины; T – возраст особи; a, d – коэффициенты уравнения роста (2); m – число локальных экстремумов; P – период биоритма; индексы 1–3 – биоритмы со средними периодами 13.4, 6.8 и 4.0 года соответственно; “–” – биоритм не обнаружен.

Сингулярный спектральный анализ показывает, что основные тренды изменения размеров раковин практически не отличаются от кривой, полученной после аппроксимации уравнением роста (1) для всех исследованных особей.

Уже при анализе кинетики удельной скорости роста в индивидуальном развитии M. margaritifera становится очевидным наличие биоритмов, сопровождающих основной тренд (рис. 2а). Более отчетливыми биоритмы становятся после выделения волновых составляющих методом сингулярного спектрального анализа. У каждого моллюска выявлено до трех закономерных биоритмов, различающихся по частоте колебаний (табл. 1, рис. 2б–г). Отсутствие низкочастотных биоритмов у некоторых моллюсков связано с невозможностью измерить необходимое для их выявления число годовых колец.

Рис. 2.

Примеры разложения временнóго ряда методом сингулярного спектрального анализа для индивидуального линейного роста Margaritifera margaritifera. Особь № 67. a – зависимость относительной скорости роста (dL/Ldt) от возраста моллюска; 1 – экспериментальные данные; 2 – аппроксимация уравнением (1). б–г – закономерные биоритмы с периодами 13.4, 6.8 и 4.0 года соответственно. Кривые – сглаживание кубическими сплайнами.

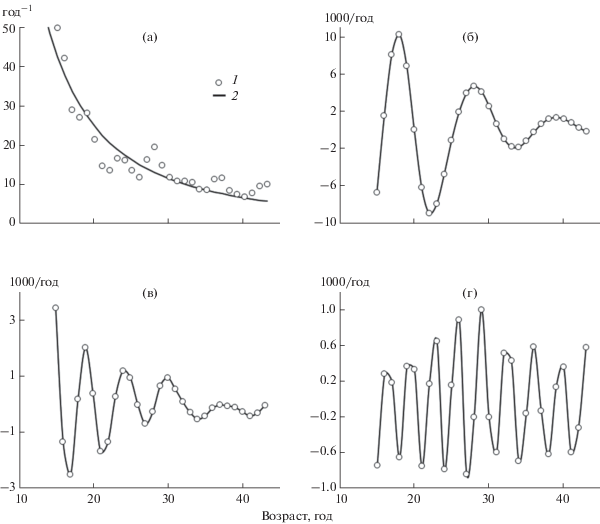
Периоды биоритмов достоверно не различаются как на протяжении онтогенеза отдельных особей, так и при сравнении разных особей: отличие коэффициента линейной регрессии периода по возрасту от нуля не достоверно; вариационный ряд, составленный из значений периодов биоритмов у разных моллюсков, согласно критерию χ2 распределен нормально. Средние значения периодов по всем моллюскам составляют 13.39 ± 0.07 года (n = 50), 6.82 ± 0.01 года (n = 84), 4.00 ± 0.01 года (n = 90).

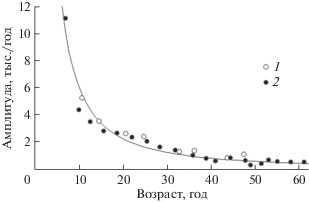
Биоритмы с периодами 13.4 и 6.8 года затухающие. Снижение средней для всех моллюсков амплитуды этих биоритмов с возрастом может быть описано степенным уравнением (3) с одинаковыми коэффициентами (рис. 3): b = 176 ± 65 тыс./год, c = –1.45 ± 0.15 (n = 28).

Рис. 3.

Зависимость средних значений амплитуды затухающих биоритмов от возраста моллюсков. 1 и 2 – биоритмы с периодами 13.4 и 6.8 года соответственно; кривая – аппроксимация степенным уравнением (3).

Амплитуда биоритмов с периодом 4 года постоянна и равна в среднем 0.76 ± 0.09 тыс./год (n = 31).

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Для характеристики роста двустворчатых моллюсков обычно используют так называемую константу роста (k) из уравнения Берталанфи (Алимов, 1981; Bauer, 1992; Зюганов и др., 1993). Мы предпочитаем использовать вместо нее другую константу, названную нами коэффициентом замедления роста (a), связанную с константой роста зависимостью a = 1 + ln k. Отметим, что если k ∼ 0, то a ∼ k. Коэффициент a выгодно отличается от константы роста k тем, что его статистическое распределение близко к нормальному, он входит в рекуррентную форму (2) в качестве коэффициента регрессии и, следовательно, может быть использован для сравнительных целей с помощью стандартных статистических методов.

Для изученных моллюсков среднее значение a равно 0.048 и, следовательно, k = 0.049, что вполне соответствует константе роста, полученной ранее для популяции р. Варзуга (Зюганов и др., 1993; Зотин А.А., Иешко, 2017).

Межпопуляционное варьирование констант роста у M. margaritifera было описано ранее (Алимов, 1981; Bauer, 1992; Зюганов и др., 1993; Hastie et al., 2000; San Miguel et al., 2004; Dunca et al., 2011; Зотин А.А., Иешко, 2017). Значение константы роста для р. Варзуга (0.049 год–1) одно из самых низких и соответствует значениям k для рек Швеции (Dunca et al., 2011) и Шотландии (Hastie et al., 2000), хотя существуют популяции M. margaritifera с более низкими значениями константы роста (до 0.01 год–1) (Bauer, 1992).

Существует тенденция уменьшения константы роста с увеличением широты места обитания моллюсков (Bauer, 1992; Зотин А.А., Иешко, 2017). Тем не менее такая зависимость имеет исключения. Так, наиболее южные популяции M. margaritifera Испании и Карелии имеют сходные значения k ≈ 0.1, несмотря на существенные различия широт (41° и 61° с.ш. соответственно) и среднегодовых температур воздуха (15 и 5°С соответственно) (CLIMATE-DATA.ORG, 2019). Отсюда следует, что температура не единственный фактор, определяющий скорость роста M. margaritifera. Какие именно факторы влияют на скорость роста моллюсков, остается неясным. Такими факторами могут быть химический состав воды, степень эвтрофикации водоема, водный режим и т.д.

Согласно современной термодинамической теории для нелинейных диссипативных структур, в частности живых систем, характерно наличие нескольких стационарных состояний (Зотин А.А., 2009; Zotin, 2014). Стремление к каждому стационарному состоянию сопровождается только одним затухающим ритмом с определенным характерным временем. В стационарном состоянии амплитуда ритма стабилизируется (Prigogine, 1972; Рубин, 1976; Малек-Мансур и др., 1980).

Использованное нами единое уравнение роста (1) по существу представляет собой уравнение релаксации системы к стационарному состоянию. Биоритмы будут описываться этим уравнением, если (1 – a)t представляет собой комплексное число, действительная часть которого описывает эволюцию системы к стационарному состоянию, а мнимая часть характеризует ритм, сопровождающий этот процесс. Низкочастотный биоритм с периодом 13.4 года аналогичен биоритму роста у морского двустворчатого моллюска Crenomytilus grayanus с периодом 10–15 лет (Золотарев, 1974). По мнению Золотарева, эти ритмы имеют экзогенную природу и опосредованы 11-летними солнечными циклами.

Остальные два биоритма, по-видимому, эндогенные и не связаны с периодическими процессами во внешней среде. Их природа, вероятно, обусловливается термодинамическими закономерностями. Можно предположить, что затухающий биоритм с периодом 6.8 года связан с процессом стремления организма к конечному стационарному состоянию. Поэтому он затухает на протяжении всего онтогенеза. Биоритм с постоянным периодом 4.0 года, скорее всего, связан с текущим стационарным состоянием, в котором биологическая система находится на протяжении всей жизни в условиях неизменной окружающей среды (Зотин А.А., 2009, 2012; Зотин А.А., Клейменов, 2013). Постоянство амплитуды в этом случае логично связать со стабильностью среды обитания в р. Варзуга, по крайней мере в последние 60–70 лет (время жизни жемчужниц).

У других популяций M. margaritifera также наблюдаются биоритмы удельной скорости роста с периодом 4 года и постоянной амплитудой, что свидетельствует о независимости этого биоритма от условий обитания моллюсков (Зотин А.А., Иешко, 2018; Zotin et al., 2018). Следует отметить, что биоритмы роста не уникальны для M. margaritifera, а были выявлены ранее у различных видов брюхоногих моллюсков и животных других таксонов. При этом, если условия среды стабильны, один из биоритмов имеет постоянную амплитуду, а другой затухающий (Зотин А.А., 2009; Зотин А.А., Клейменов, 2013).

Конечно, выявленные биоритмы могут иметь и другую, чисто биологическую природу, например могут быть результатом реакции организма на какие-либо не известные нам периодические процессы в окружающей среде. Для получения окончательного ответа на этот вопрос требуется провести дополнительные исследования на других популяциях и видах животных.

Выполнено А.А. Зотиным в рамках раздела Государственного задания ИБР РАН, № 0108-2020-0003.

Список литературы

  1. Алимов А.Ф. Функциональная экология пресноводных двустворчатых моллюсков. Л.: Наука, 1981. 248 с.

  2. Васильев В.А. Стационарные диссипативные структуры // Термодинамика биологических процессов. М.: Наука, 1976. С. 186–198.

  3. Золотарев В.Н. Многолетние ритмы роста раковин мидии Граяна // Экология. 1974. № 3. С. 76–80.

  4. Зотин А.А. Статистическая оценка параметров аллометрических уравнений // Изв. РАН. Сер. биол. 2000. № 5. С. 517–524.

  5. Зотин А.А. Закономерности роста и энергетического обмена в онтогенезе моллюсков: Автореф. дис. докт. биол. наук. М.: ИБР РАН, 2009. 30 с.

  6. Зотин А.А. Особенности реализации принципа наименьшей диссипации энергии в индивидуальном развитии // Изв. РАН. Сер. биол. 2012. № 3. С. 261–269.

  7. Зотин А.А., Иешко Е.П. Сравнительный анализ роста Margaritifera margaritifera (Bivalvia) из разных популяций Карелии и Кольского полуострова // Изв. РАН. Сер. биол. 2017. № 1. С. 5–9.

  8. Зотин А.А., Иешко Е.П. Биоритмы роста пресноводной жемчужницы Margaritifera margaritifera (Bivalvia, Margaritiferidae). Популяция р. Сюскюянйоки (Карелия) // Онтогенез. 2018. Т. 49. № 4. С. 233–241.

  9. Зотин А.А., Клейменов С.Ю. Эндогенные биоритмы удельной скорости роста в индивидуальном развитии Lymnaea stagnalis (Lymnaeidae, Gastropoda) // Изв. РАН. Сер. биол. 2013. № 1. С. 5–14.

  10. Зотин А.И. Термодинамический подход к проблемам развития, роста и старения. М.: Наука, 1974. 183 с.

  11. Зотин А.И. Диссипативные структуры и ψu-функции // Термодинамика биологических процессов. М.: Наука, 1976. С. 203–205.

  12. Зотин А.И., Зотина Р.С. Феноменологическая теория развития, роста и старения организма. М.: Наука, 1993. 364 с.

  13. Зюганов В.В., Зотин А.А., Третьяков В.А. Жемчужницы и их связь с лососевыми рыбами. М.: ЦНИИТЭИлегпром, 1993. 134 с.

  14. Ивантер Э.В., Коросов А.В. Элементарная биометрия. Петрозаводск: Изд-во ПетрГУ, 2010. 104 с.

  15. Лампрехт И. Диссипативные структуры в физике, химии и биологии // Термодинамика биологических процессов. М.: Наука, 1976. С. 175–186.

  16. Малек-Мансур М., Николис Г., Пригожин И. Неравновесные фазовые переходы в химических системах // Термодинамика и кинетика биологических процессов. М.: Наука, 1980. С. 59–83.

  17. Рубин А.Б. Термодинамика биологических процессов. М.: МГУ, 1976. 240 с.

  18. Сипачев С.Г. Ритмичность роста животных. Тюмень: ТГПИ, 1970. 351 с.

  19. Bauer G. Variation in life span and size of the freshwater pearl mussel // J. Animal Ecol. 1992. V. 61. P. 425–436.

  20. CLIMATE-DATA.ORG. 2019. https://ru.climate-data.org/

  21. Dunca E., Söderberg H., Norrgrann O. Shell growth and age determination in the freshwater pearl mussel Margaritifera margaritifera in Sweden: natural versus limed streams // Ferrantia. 2011. V. 64. P. 48–58.

  22. Haken H. Synergetics. Introduction and advanced topics. Pt I. An introduction. Nonequilibrium phase transitions and self-organization in physics, chemistry and biology. Second enlarged edition. Hendelberg; New York: Springer-Verlag, 1978. 401 p.

  23. Hastie L C., Young M.R., Boon P.J. Growth characteristics of freshwater pearl mussels, Margaritifera margaritifera (L.) // Freshw. Biol. 2000. V. 43. P. 243–256.

  24. Nicolis G. Fluctuations around non-equilibrium states in open non-linear systems // J. Stat. Phys. 1972. V. 6. № 2/3. P. 195–222.

  25. Nicolis G., Prigogine I. Self-organization in nonequilibrium systems: from dissipative structures to order through fluctuations. N. Y.: Wiley Intersci., 1977. 512 p.

  26. Prigogine I. La thermodynamique de la vie // La Recherche. 1972. V. 3. № 24. P. 547–562.

  27. Prigogine I., Nicolis G. Biological order, structure and instabilities // Quart. Rev. Biophys. 1971. V. 4. № 2/3. P. 107–148.

  28. San Miguel E., Monserrat S., Fernández C., Amaro R., Hermida M., Ondina P., Altaba C.R. Growth models and longevity of freshwater pearl mussels (Margaritifera margaritifera) in Spain // Can. J. Zool. 2004. V. 82. P. 1370–1379.

  29. Zotin A.A. Why linear thermodynamics does describe change of entropy production in living systems? // Nat. Sci. 2014. V. 6. P. 495–502.

  30. Zotin A.A. The united equation of animal growth // Amer. J. Life Sci. 2015. V. 3. № 5. P. 345–351.

  31. Zotin A.A., Zotin A.I. Thermodynamic bases of developmental processes // J. Non-Equilib. Thermodyn. 1996. V. 21. № 4. P. 307–320.

  32. Zotin A.A., Zotin A.I. Phenomenological theory of ontogenesis // Int. J. Dev. Biol. 1997. V. 41. № 6. P. 917–921.

  33. Zotin A.A., Murzina S.A., Ieshko E.P. Growth biorhythms in the freshwater pearl mussel Margaritifera margaritifera (Bivalvia, Margaritiferidae). Livojoki river population (Karelia) // Knowl. Manag. Aquat. Ecosyst. 2018. V. 419. P. 44–51.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия биологическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал