1. На главную
  2. Электронные версии
  3. Известия РАН. Серия биологическая
  4. № 1, 2021

Известия РАН. Серия биологическая, 2021, № 1, стр. 3-18

Математическое моделирование популяционной динамики на основе рекуррентных уравнений: результаты и перспективы. Ч. I

Е. Я. Фрисман 1, О. Л. Жданова 1, 2, М. П. Кулаков 1, Г. П. Неверова 1, 2, *, О. Л. Ревуцкая 1

1 Институт комплексного анализа региональных проблем ДВО РАН
679016 Биробиджан, ул. Шолом-Алейхема, 4, Россия

2 Институт автоматики и процессов управления ДВО РАН
690041 Владивосток, ул. Радио, 5, Россия

* E-mail: galina.nev@gmail.com

Поступила в редакцию 16.06.2020
После доработки 27.07.2020
Принята к публикации 27.07.2020

Полный текст (PDF)

Аннотация

В обзоре, состоящем из двух частей, описаны подходы к моделированию динамики популяций с использованием дискретных во времени моделей. Представлена эволюция научных идей по пути усложнения дискретных во времени моделей – от модели Мальтуса до современных моделей, учитывающих множество факторов, влияющих на популяционную структуру и динамику и отражающих большой спектр возможных динамических режимов. Приведены наиболее важные и интересные результаты, полученные авторским коллективом в ходе применения рекуррентных уравнений к анализу биологических систем. В первой части обзора рассмотрены динамические эффекты, к которым приводят плотностно-зависимая регуляция, усложнение возрастной структуры, учет половой структуры и влияние внешних факторов.

“Золотой век” математической биологии начался в первой половине ХХ в. феерическим “всплеском” работ, надолго определивших развитие теоретической экологии и математической популяционной генетики, основы синтетической теории эволюции (Haldane, 1924; Lotka, 1925; Fisher, 1930; Volterra, 1931; Wright, 1931; Kostitzin, 1937; и др.). Математической базой этих работ были модели, построенные с помощью дифференциальных уравнений и удачно описывающие многие феномены, наблюдающиеся в биологических сообществах: колебания численностей, конкурентное вытеснение, полиморфное разнообразие и многое другое.

В начале 1970-х гг. в основном благодаря базовым работам Р. Мэя (May, 1975) и А.П. Шапиро (Шапиро, 1972; Шапиро, Луппов, 1983) математическая популяционная биология пополнилась достаточно простыми, но весьма эффектными моделями, основанными на рекуррентных уравнениях, известных также как модели с дискретным временем или отображения. Эти модели представлялись достаточно адекватными для описания динамики видов, характеризующихся сезонным периодом размножения и стадийностью развития. Если для математиков рекуррентные уравнения служат подспорьем или одним из методов изучения динамики сложных моделей с непрерывным временем, то для математических биологов и системных экологов они выступают самостоятельным объектом исследования, удобным для моделирования динамики популяций. Популярность рекуррентных уравнений связана с довольно простой техникой их построения (например, представление жизненного цикла в виде графа), доступными методами исследования (фазовый портрет, лестница Ламерея и др.), а также несложной интерпретацией модельных уравнений и результатов моделирования. Оказалось, что эти “простенькие” модели даже в одномерном случае, обладают колоссальным разнообразием динамических режимов, сложно эволюционирующих при изменении параметров модели, вплоть до хаотической динамики. Важно, что аналогичное динамическое поведение в моделях с непрерывным временем отмечается в автономных (с постоянными коэффициентами) системах обыкновенных уравнений размерностью не менее 3 или неавтономных с размерностью не менее 2.

Проведены обзор и систематизация основных результатов исследования рекуррентных уравнений в контексте изучения причин и механизмов изменений общей численности или структуры популяций. Данный обзор не претендует на всесторонний охват большинства результатов. Значительная часть приведенных здесь результатов получена либо коллективом авторов этой статьи, либо совместно с другими исследователями. Многие результаты известны в области динамических систем, а также биофизики и экологии. Однако статья содержит ряд довольно свежих результатов, связанных с развитием классических моделей и использованием современных методов исследования динамических систем применительно к популяционной экологии.

ХАРАКТЕР ДИНАМИКИ ЧИСЛЕННОСТИ ПОПУЛЯЦИЙ С НЕПЕРЕКРЫВАЮЩИМИСЯ ПОКОЛЕНИЯМИ

Для однолетних растений, многих видов насекомых, некоторых видов рыб, земноводных и пресмыкающихся каждая отдельная популяция представляет собой один возрастной класс, и смежные поколения такой популяции не перекрываются. Если условия среды практически не меняются во времени, то численность некоторого поколения будет определяться только численностью предыдущего поколения. Обозначив через Nn численность п-го поколения, можно записать следующее детерминированное уравнение, описывающее динамику численности такой популяции:

${{N}_{n}}_{{ + 1}} = F({{N}_{n}}),$
где F – функция воспроизводства. Простейший вид этого уравнения для
$F({{N}_{n}}) = r{{N}_{n}}$
является моделью Мальтуса, где r – некоторая постоянная. При этом предполагается, что каждая особь оставляет в следующем поколении в среднем r потомков независимо от численности родительской популяции:

(1)
${{N}_{n}}_{{ + 1}} = r{{N}_{n}}.$

Решение этого уравнения – геометрическая прогрессия со знаменателем r и начальным членом N0, что фактически идентично экспоненциальному росту численности популяции в отсутствие лимитирующих факторов.

Хорошо известно, что долгий экспоненциальный рост численности в природе никогда не наблюдается. Рано или поздно сказывается действие лимитирующих факторов, поэтому r в уравнении (1) оказывается функцией численности. Положим r = af(N), где f(N) – функция, описывающая лимитирование, а – параметр, называемый репродуктивным потенциалом популяции и характеризующий скорость роста популяции в пустоту (т.е. а выбирается так, чтобы выполнялось равенство f(0) = 1). Теперь вместо уравнения (1) получаем

(2)
${{N}_{n}}_{{ + 1}} = a{{N}_{n}}f({{N}_{n}}).$

Такие модели исследовали А.П. Шапиро (Шапиро, 1972; Шапиро, Луппов, 1983) и Р. Мэй (May, 1975). Они показали, что динамика численности популяции, описываемая уравнением (2), может быть весьма сложной, если функция F(N) = aNf(N) убывает при больших значениях N достаточно быстро (например, быстрее, чем 1/N2). Особенность этих моделей заключается в том, что при увеличении репродуктивного потенциала популяции происходит потеря устойчивости равновесия, которая сопровождается возникновением двухлетних колебаний.

Конкретизируя вид функции f(N), для уравнения (2) численно можно построить траектории при различных начальных условиях. Хорошо изучены дискретный аналог модели Ферхюльста, для которого f(N) = 1 – kN, и модель, предложенная ихтиологом У. Рикером (Ricker, 1954), для которой f(N) = exp(–kN). При исследовании уравнения (2) обычно исключают масштабный параметр k и переходят к безразмерным переменным: “относительным” численностям x = kN. В этом случае дискретный аналог модели Ферхюльста и модель Рикера соответственно имеют вид

${{x}_{n}}_{{ + 1}} = a{{x}_{n}}(1--{{x}_{n}}),\,\,\,\,~{{x}_{n}}_{{ + 1}} = a{{x}_{n}}\exp (--{{x}_{n}}).$

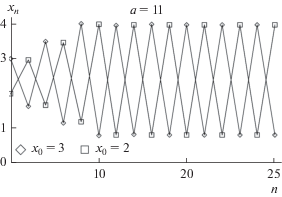
На рис. 1 приведены решения модели Рикера при различных начальных условиях: два 2-летних цикла с различными фазами колебаний. Соответственно, такая система оказывается бистабильной: согласно одним начальным условиям решения сходятся к одному 2-летнему циклу, а согласно другим – к другому (рис. 1). О такой бистабильности свидетельствуют результаты лабораторных экспериментов (Henson et al., 1998), показывающие, что при одной и той же начальной численности и схожих, но не идентичных условиях в популяциях мучного хрущака Tribolium castaneum могут наблюдаться два разных противофазных периодических режима, т.е. наблюдается фазовая мультистабильность.

Рис. 1.

Траектории модели Рикера при различных начальных условиях (значениях x0): 2-летние циклы разных фаз. x – относительные значения численности популяции, n – номер поколения, a – репродуктивный потенциал.

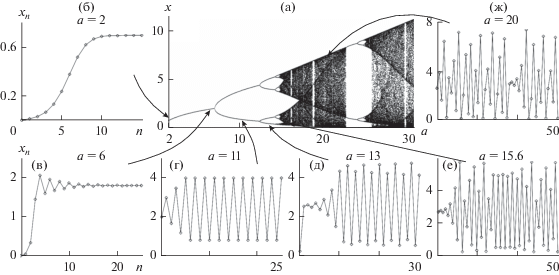
При дальнейшем увеличении репродуктивного потенциала решения уравнения сходятся к устойчивым 4-летним циклам, затем к 8-летним циклам и т.д. Описанные изменения характера динамики численности принято называть первой серией бифуркаций, а сценарий образования этих циклов – сценарием удвоения периода, универсальным для любого унимодального отображения (универсальность Фейгенбаума) (Feigenbaum, 1983). Он приводит и к соответствующему усложнению фазовой мультистабильности. При еще больших значениях параметра а поведение численности популяции теряет сколько-нибудь регулярный характер и становится хаотическим. Зоны хаотического поведения перемежаются с “окнами” периодического, т.е. регулярного поведения.

Для любого конкретного вида функции f(N) в уравнении (2) численно можно построить бифуркационную диаграмму, характеризующую предельные траектории в зависимости от коэффициента а (рис. 2а). На рис. 2б–ж приведены решения уравнения Рикера (последовательности, порождаемые рекуррентным уравнением при разных значениях а и различных начальных значениях xn).

Рис. 2.

Бифуркационная диаграмма (а) и решения (б–ж) уравнения Рикера при разных значениях репродуктивного потенциала – параметра a. б – монотонное схождение к равновесию, в – затухающие колебания, г – 2-летний цикл, д – 4-летний цикл, е и ж – нерегулярная динамика.

Частный случай, обобщающий уравнения Ферхюльста и Рикера, – трехпараметрическая модель Хассела (Hassell, 1975):

${{N}_{n}}_{{ + 1}} = {{a{{N}_{n}}} \mathord{\left/ {\vphantom {{a{{N}_{n}}} {{{{(1 + k{{N}_{n}})}}^{\beta }}}}} \right. \kern-0em} {{{{(1 + k{{N}_{n}})}}^{\beta }}}}.$

Эта модель позволяет исследовать динамику численности популяции при различной интенсивности экологического лимитирования, характеризующегося параметром β, увеличение которого приводит к росту скорости убывания f(x)=1/(1 + x)β при больших значениях х. Так, при малых значениях β (β < 2), т.е. при слабом лимитировании, немонотонных режимов динамики численности не наблюдается ни при каких значениях а, характеризующего скорость размножения вида. Это справедливо, например, при β = 1, т.е. для случая, когда модель Хассела переходит в модель Бивертона–Холта. Однако при больших значениях β (β > 3) монотонное увеличение параметра а приводит к осуществлению первой серии бифуркаций, а затем и к возникновению хаотического режима динамики, т.е. к бифуркациям, аналогичным в модели Рикера.

При больших фиксированных значениях а (а ≥ 30) рост параметра β приводит к таким же изменениям режима динамики численности популяции, что и рост параметра а при фиксированных значениях β. Различие заключается в том, что при росте β бифуркации происходят на фоне снижения равновесного уровня численности, тогда как при росте а – на фоне его увеличения. Таким образом, пространство параметров а и β разбивается на ряд областей, каждая из которых характеризуется своим типом динамического поведения.

Исследование режимов динамического поведения в моделей Рикера, Хасселла и других позволяет обнаружить некоторые общие закономерности, проявляющиеся при достаточно больших значениях репродуктивного потенциала и степени экологического лимитирования, когда динамика численности может оказаться хаотической или близкой к ней (интервально-периодической). Если начальное значение численности невелико, то достаточно продолжительное время будет наблюдаться ее медленный рост (который может сопровождаться в отдельных поколениях даже небольшими спадами), после чего произойдет резкое увеличение численности, сопровождающееся в следующей генерации значительным уменьшением ее до значения, близкого к начальному. Эти периодические “переломы” не будут, однако, возвращать популяцию точно на начальный уровень. Следовательно, несмотря на явный периодический характер изменения численности, не будет обнаружено полных совпадений ни значений численности, ни числа генераций в фазе возрастания (Шлюфман и др., 2013). Подобное нестрого периодическое поведение численности характерно для многих естественных популяций высших организмов, особенно насекомых (например, саранчи, кузнечиков, ночных мотыльков).

Часто попытки применения одномерных моделей с дискретным временем к описанию и прогнозу динамики конкретных природных популяций оказывались малопродуктивными: модельные кривые, отлавливая тенденции изменения численности, статистически плохо описывали наблюдаемую динамику реальных популяций (Шапиро, Луппов, 1983; Dennis, Taper, 1994; Myers et al., 1999; Фрисман и др., 2007, 2015а; Nedorezov, Sadykova, 2008; Недорезов, 2010; Тарасов и др., 2012). В ряде случаев модельное описание удавалось улучшить при введении в уравнения запаздывания (Недорезов, 1986; Turchin, 1990, 2003; Исаев и др., 2001; Berryman, Turchin, 2001; Nedorezov, 2012; Sadykova, Nedorezov, 2013; Nedorezov, Sadykova, 2015). Регуляция с запаздыванием возникает в природных популяциях в результате межвидового взаимодействия или в случаях, когда высокая плотность популяции негативно сказывается на воспроизводстве следующего поколения (Prout, MсСhesney, 1985; Turchin, 1990; Williams, Liebhold, 1995). Наиболее убедительные результаты были получены для модели Рикера (Морана–Рикера) и ее модификации с запаздыванием (Kendall et al., 1999; Turchin, 2003; Turchin et al., 2003; Bechtol, Kruse, 2009; Sadykova, Nedorezov, 2013; Nedorezov, Sadykova, 2015). В частности, была предпринята попытка описания и анализа динамики Zeiraphera diniana Gn. на основе модели Рикера при различных значениях лага (Sadykova, Nedorezov, 2013; Nedorezov, Sadykova, 2015).

ХАРАКТЕР ДИНАМИКИ ЧИСЛЕННОСТИ ПОПУЛЯЦИЙ С НЕПЕРЕКРЫВАЮЩИМИСЯ ПОКОЛЕНИЯМИ С УЧЕТОМ ВОЗРАСТНОЙ СТРУКТУРЫ (СТАДИЙНОСТИ РАЗВИТИЯ ОСОБЕЙ)

При моделировании динамики популяции помимо сезонности размножения необходимо учитывать ее возрастную структуру, поскольку выживаемость и степень участия в размножении особей разного возраста различаются. Действительно, в жизненном цикле любого организма можно выделить несколько возрастных ступеней, определяемых в некоторых единицах времени, например в годах (Leslie, 1945; Caswell, 2001). В случае когда возраст особей неизвестен, классификация особей в структурированной популяции происходит не по их хронологическому возрасту, а по стадии развития (Lefkovitch, 1965; Caswell, 2001; Логофет, Клочкова, 2002; Logofet, 2008). Тогда популяция распадается на некоторое число групп, способ разбиения на которые, как правило, определяется биологическими особенностями организмов. Так, модель динамики популяции с неперекрывающимися поколениями xn + 1= axnexp(–xn) с учетом стадийности развития особей принимает вид

(3)
$\begin{gathered} {{X}_{{n + 1}}} = B{{Y}_{n}}\exp ( - \alpha {{X}_{n}} - \beta {{Y}_{n}}), \\ {{Y}_{{n + 1}}} = s{{X}_{n}}, \\ \end{gathered} $
где Xn – численность годовалых особей, Yn – численность половозрелых особей в n-м периоде размножения (точнее, к началу периода размножения в n-м году), B – репродуктивный потенциал половозрелых особей, α и β – коэффициенты, характеризующие степени воздействия численностей особей ювенильной и зрелой групп на уменьшение рождаемости, s – выживаемость особей на втором году жизни. Исследование модели (3) удобно проводить в пространстве параметров ρ = α/(sβ) и r = sB, где ρ описывает относительный вклад младшей возрастной группы в лимитирование воспроизводства, а r характеризует репродуктивный потенциал особей с учетом выживаемости молоди.

Оказалось, что нетривиальное равновесие системы (3) может терять устойчивость как по сценарию удвоения периода, так и по сценарию Неймарка–Сакера – дискретного аналога бифуркации Пуанкаре–Андронова–Хопфа, приводящего к квазипериодической динамике (Кузнецов и др., 2012). В результате дискретные во времени модели с учетом стадийной структуры способны описывать не только длиннопериодические колебания, которые наблюдаются в моделях с непрерывным временем, но и “зашумленные колебания”.

Современные вычислительные технологии позволяют идентифицировать области различных динамических режимов в пространствe параметров модели и получить карты динамических режимов. Карта динамических режимов модели (3), приведенная на рис. 3, в своей левой части демонстрирует картину, характерную для бифуркации Неймарка–Сакера, которая состоит в возникновении области квазипериодических режимов Q с погруженной в нее системой языков Арнольда, в правой части – каскад бифуркаций удвоения периода (рис. 3а). Следовательно, если уровень рождаемости лимитируется преимущественно численностью зрелых особей, тогда возникают квазипериодические колебания. Когда рождаемость уменьшается с ростом численности ювенильной группы, т.е. ρ > 1, то увеличение репродуктивных способностей особей приводит к периодическим колебаниям численности.

Рис. 3.

а – карта динамических режимов системы (3). Числа – периоды колебаний численности, Q – квазипериодическая динамика, C – хаотическая динамика, 0 – вырождение популяции. б – бассейны притяжения сосуществующих динамических режимов в области мультистабильности, дополненные траекториями модели при разных начальных условиях.

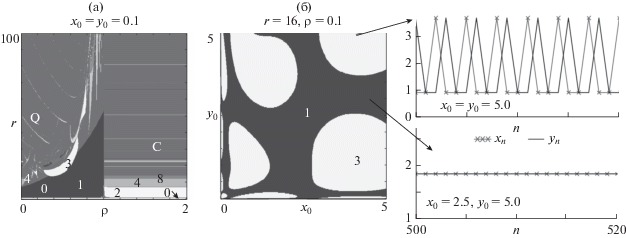
На рис. 3б представлены бассейны притяжения динамических режимов модели (3) в области мультистабильности, где 3-летний цикл устойчив одновременно с равновесным состоянием. При одних начальных условиях система стабилизируется, а при других демонстрирует трехлетние колебания. Отметим, что подобная мультистабильность была показана ранее, в частности, для двумерного отображения Эно и некоторых его модификаций (Saucedo-Solorio et al., 2002; Shrimali et al., 2008; Pisarchik, Feudel, 2014; и др.). Для отображения Эно продемонстрирован механизм рождения 3-летнего цикла и предельной инвариантной кривой на его основе, сосуществующих с неподвижной точкой (Romera et al., 2001).

Мультистабильность в рамках рекуррентных моделей динамики структурированных популяций позволяет по-новому взглянуть на общебиологические проблемы и отметить существующие фундаментальные закономерности, которые до этого оставались незамеченными. В частности, мультистабильность позволяет объяснить наблюдаемые различия в динамике численности популяций одного вида, обитающих в практически идентичных условиях. В рамках локальной популяции явление мультистабильности дает возможность объяснить как возникновение, так и исчезновение колебаний численности, а также смену периода наблюдаемых колебаний. К наиболее ярким примерам смен динамических режимов относятся исчезновения циклов в популяциях лемминга (Coulson, Malo, 2008; Kausrud et al., 2008; White, 2011) и некоторых видов полевок (Henttonen, Wallgren, 2001; Cornulier et al., 2013). При этом следует понимать, что изменение в модели характера динамики может произойти не только в случае существования нескольких режимов динамики при одних и тех же значениях параметров, но и вследствие фазовой мультистабильности, когда под действием возмущения переменой уравнения модельная траектория осуществляет прыжки по бассейнам притяжения разных фаз одного и того же динамического режима. При этом чем больше период наблюдаемых колебаний, тем больше фаз этого цикла со своими бассейнами притяжения может существовать, что в условиях нестационарной среды будет усложнять динамику популяции.

ДИНАМИКА ЧИСЛЕННОСТИ ПОПУЛЯЦИИ С ДВУМЯ СТАДИЯМИ РАЗВИТИЯ

Рассмотрим популяцию с возрастной структурой, которая к началу очередного сезона размножения может быть представлена совокупностью двух классов: младшего с численностью Xn и старшего с численностью Yn в n-й сезон размножения. Период размножения заканчивается появлением новорожденных особей следующего поколения. Будем предполагать, что времени между двумя последовательными периодами размножения достаточно для развития новорожденных до состояния младшего возраста. Допустим, что выживаемость и репродуктивная способность особей старшего возрастного класса не зависят от их хронологического возраста. Это правомерно для организмов с небольшим временем жизни, включающим в себя 2–3 периода размножения, как у многих насекомых, рыб, мелких млекопитающих, 2- и 3-летних растений и др. Можно записать следующую систему уравнений, описывающую динамику рассматриваемых возрастных групп в смежных поколениях:

(4)
$\left\{ \begin{gathered} {{X}_{{n + 1}}} = {{A}_{1}}\left( {{{X}_{n}},{{Y}_{n}}} \right){{X}_{n}} + {{A}_{2}}\left( {{{X}_{n}},{{Y}_{n}}} \right){{Y}_{n}} \hfill \\ {{Y}_{{n + 1}}} = B\left( {{{X}_{n}},{{Y}_{n}}} \right){{X}_{n}} + C\left( {{{X}_{n}},{{Y}_{n}}} \right){{Y}_{n}} \hfill \\ \end{gathered} \right.,$
где A1 и A2 – рождаемости, B и С – выживаемости младшего и старшего возрастных классов соответственно. Если A1, A2, B и С считаются константами, то система (4) – частный случай линейной матричной модели Лефковича (Lefkovitch, 1965; Caswell, 2001), активно развиваемой как в теоретическом, так и в прикладном плане во многих исследованиях, например в работах Д.О. Логофета с соавт. (Logofet et al., 2006; Логофет, Белова, 2007; Логофет и др., 2017; Logofet, 2019). В частности была предложена матричная модель, ориентированная на описание динамики ценопопуляции незабудочника Eritrichium caucasicum, а также проведена калибровка модели (Логофет и др., 2016; Logofet et al., 2018).

Вместе с тем у большинства биологических видов наблюдается плотностно-зависимая регуляция роста численности популяции (Lack, 1954; Гиммельфар и др., 1974; Дажо, 1975; Одум, 1975; Уильямсон, 1975; Свирежев, Логофет, 1978; Boer, Reddingius, 1996; Gurney, Nisbet, 1998; Inchausti, Ginzburg, 1998; Ginzburg, Colyvan, 2004; Barraquand et al., 2017). Основное проявление плотностно-зависимой регуляции рождаемости – стресс-синдром, приводящий к снижению половой активности и уменьшению плодовитости особей, вплоть до рассасывания части заложенных эмбрионов. В частности, это характерно для подверженных сильным колебаниям численности видов, например для леммингов и полевок (Дажо, 1975; Чернявский, Лазуткин, 2004; Фрисман и др., 2010a; Новиков и др., 2012; Krebs, 2013). При моделировании динамики популяций таких видов выживаемости можно считать константами B(X, Y) = b, C(X, Y) = c, а рождаемость по аналогии с моделью Рикера можно записать в виде

${{A}_{i}}(X,Y) = {{r}_{i}}\exp ( - \alpha X - \beta Y),$
где r1 и r2– репродуктивные потенциалы младшей и старшей возрастных групп, α и β – коэффициенты, характеризующие интенсивности воздействия численностей неполовозрелого и половозрелого возрастных классов на уменьшение рождаемости. С учетом этого и после перехода к безразмерным переменным x = bβX и y = βY модель (4) может быть преобразована к виду
(5)
$\left\{ \begin{gathered} {{x}_{{n + 1}}} = (a{}_{1}{{x}_{n}} + {{a}_{2}}{{y}_{n}})\exp ( - \rho {{x}_{n}} - {{y}_{n}}), \hfill \\ {{y}_{{n + 1}}} = {{x}_{n}} + c{{y}_{n}}, \hfill \\ \end{gathered} \right.$
где a1 = r1 и a2 = br2 – новые обозначения коэффициентов, характеризующих репродуктивные потенциалы, а ρ = α/(bβ) описывает относительный вклад младшей возрастной группы в лимитирование воспроизводства. Модель (5) в первую очередь ориентирована на описание динамики популяций, характеризующихся быстрой скоростью созревания молоди. В таких популяциях зрелые особи приносят несколько пометов за сезон, а подросшие сеголетки в течение этого же сезона достигают зрелости, начинают размножаться и приносить потомство.

Отметим, что частный случай модели (5) при а1 = 0 соответствует ситуации, когда молодь достигает зрелости и начинает участвовать в размножении через год (Фрисман и др., 2010в; Frisman et al., 2011; Ревуцкая и др., 2016; Neverova et al., 2018).

Было также проведено исследование модели (5) и показано, что падение рождаемости с ростом численности особей оказывается эффективным механизмом регуляции роста численности (Фрисман и др., 2015б; Frisman et al., 2016; Neverova et al., 2019). Однако при больших репродуктивных возможностях и высокой выживаемости особей падение рождаемости с ростом численности может привести к потере устойчивости и возникновению колебаний. Так, при относительно больших значениях a2 или ρ (ρ ≥ 1), т.е. в случае когда вклад в размножение вносит в основном старший возрастной класс, а лимитирование рождаемости осуществляется преимущественно младшим возрастным классом, потеря устойчивости, как и в исходной одномерной модели Рикера, сопровождается появлением двухлетних колебаний и последующим каскадом удвоения периода. При этом чем больше значение ρ, тем при более низком значении репродуктивного потенциала возникают колебания.

При больших значениях a1 или малых значениях ρ, т.е. в случаях когда основной вклад в размножение вносят сеголетки, потеря устойчивости сопровождается появлением квазипериодических колебаний (рис. 4а). Интенсивное размножение сеголеток и уменьшение рождаемости с ростом численности размножающихся особей способны привести к возникновению сложноорганизованных колебаний численности. Именно этот механизм, по-видимому, определяющий в поведении численности мелких млекопитающих, таких как лемминги и некоторые полевки (Чернявский, Лазуткин, 2004; Krebs, 2013).

Рис. 4.

а – эскиз параметрического портрета в пространстве параметров a1 и a2, характеризующих репродуктивные потенциалы младшей и старшей возрастных групп соответственно, и примеры динамических режимов модели (5). При значениях параметров, попадающих в криволинейный серый треугольник, наблюдается переход к равновесию. Пример такой динамики для значений параметров, соответствующих точке А, приведен на графиках А. При значениях параметров, лежащих над верхней кривой, наблюдаются квазипериодические колебания: точка В и соответствующие графики В. При значениях параметров, находящихся под нижней кривой, наблюдается циклическая динамика: точка С и соответствующие графики С – колебания с периодом 2. x, y – относительные численности младшего и старшего возрастных классов, n – номер поколения. б – карта динамических режимов модели (5) в пространстве параметров a1 и a2, Числа – периоды колебаний численности, НД – нерегулярная динамика.

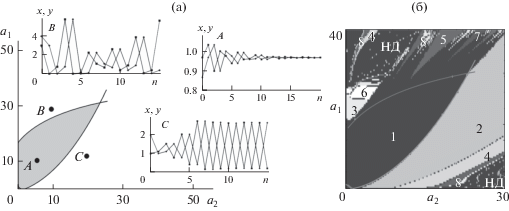
В параметрическом пространстве модели (5) наряду с нерегулярной динамикой существуют области с регулярной динамикой – периодическими колебаниями (рис. 4б). Важное различие в поведении систем динамики популяций с перекрывающимися поколениями и популяций с неперекрывающимися поколениями – реализация каскада бифуркаций удвоения периода не только с ростом репродуктивных потенциалов особей, но и при изменении значений параметра, характеризующего лимитирование рождаемости.

В ходе исследования моделей с возрастной структурой была обнаружена мультистабильность. Например, возможен переход к устойчивому нетривиальному равновесию или устойчивым 3- или 4-летним колебаниям. Тип динамического режима определяется в этом случае начальными условиями, небольшая вариация которых способна изменить тип динамики. Отметим, что периодические изменения численности с преобладанием 3–4-летних циклов наблюдались в популяциях леммингов и некоторых видов полевок рода Clethrionomys, обитающих в лесотундре и северной части лесной зоны Голарктики (Чернявский, Лазуткин, 2004).

МУЛЬТИСТАБИЛЬНОСТЬ В МОДЕЛЯХ ДИНАМИКИ ЧИСЛЕННОСТИ ПОПУЛЯЦИИ С УЧЕТОМ ВОЗРАСТНОЙ И ПОЛОВОЙ СТРУКТУР

Исследованием дискретных во времени математических моделей динамики численности популяций с возрастной и половой структурой занимались многие авторы (Caswell, Weeks, 1986; Lindstrom, Kokko, 1998; Caswell, 2001; Shyu, Caswell, 2016; и др.). В результате изучения соответствующих моделей было показано (Frisman et al., 1982; Caswell, Weeks, 1986; Lindstrom, Kokko, 1998; Caswell, 2001; Фрисман и др., 2010б; Revutskaya et al., 2012), что на характер динамики популяции влияют такие факторы, как размер гарема, плотностно-зависимая регуляция численности, конкуренция самцов за самку, особенности территориального распределения самок и самцов.

Рассмотрим популяцию с сезонным характером размножения, состоящую из трех групп: младшей, включающей в себя неполовозрелых особей (P), и двух старших, представленных половозрелыми самками (F) и самцами (M) в n-й сезон размножения. Предполагается, что времени между двумя последовательными периодами размножения достаточно для развития особей младшего возраста до половозрелого состояния.

Предполагается, что рождаемость зависит от соотношения численностей половозрелых самок и самцов и может быть описана с помощью функции образования пар (Caswell, Weeks, 1986):

$c({{F}_{n}},{{M}_{n}}) = {{2{{F}_{n}}{{M}_{n}}} \mathord{\left/ {\vphantom {{2{{F}_{n}}{{M}_{n}}} {({{{{F}_{n}}} \mathord{\left/ {\vphantom {{{{F}_{n}}} h}} \right. \kern-0em} h} + {{M}_{n}})}}} \right. \kern-0em} {({{{{F}_{n}}} \mathord{\left/ {\vphantom {{{{F}_{n}}} h}} \right. \kern-0em} h} + {{M}_{n}})}},$
где h соответствует среднему размеру гарема и характеризует тип брачных отношений в популяции (при моногамии h = 1, при полигинии h > 1, при полиандрии h < 1). Для того чтобы избежать “завышения” рождаемости для популяций, в которых самки дают потомство 1 раз за сезон размножения, функцию образования пар можно преобразовать к виду (Bessa-Gomes et al., 2010)

$c({{F}_{n}},{{M}_{n}}) = \min [{{F}_{n}},\,{{2{{F}_{n}}{{M}_{n}}} \mathord{\left/ {\vphantom {{2{{F}_{n}}{{M}_{n}}} {({{{{F}_{n}}} \mathord{\left/ {\vphantom {{{{F}_{n}}} h}} \right. \kern-0em} h} + {{M}_{n}})}}} \right. \kern-0em} {({{{{F}_{n}}} \mathord{\left/ {\vphantom {{{{F}_{n}}} h}} \right. \kern-0em} h} + {{M}_{n}})}}]$.

Условие переключения функции образования пар соответствует балансу полов в популяции и имеет вид F = hM, где hM – число самок, которое может быть потенциально оплодотворено самцами численностью M со средним размером гарема h.

Модели с функцией образования пар могут применяться для анализа и описания динамики насекомых, пресмыкающихся, птиц и млекопитающих (Frisman et al., 1982; Molnar et al., 2008; Miller, Inouye, 2011; Gerber, White, 2014).

Предположим, что выживаемости неполовозрелых самок и самцов до момента достижения половой зрелости не различаются и линейно убывают с ростом численностей возрастных классов, причем влияние половозрелых самок и самцов полагается одинаковым:

${{w}_{1}} = {{w}_{2}} = 1 - \alpha P - \beta (F + M),$
где α и β – коэффициенты, характеризующие интенсивность снижения выживаемости молоди, которое вызвано конкурентным взаимодействием между половозрастными классами соответственно. Будем полагать, что при отрицательных значениях, возникающих при больших численностях, функция выживаемости молоди обнуляется. С биологической точки зрения это можно интерпретировать как гибель приплода соответствующего года в силу высокой внутривидовой конкуренции за ресурсы.

С учетом описанных предположений модель может быть записана системой трех рекуррентных уравнений:

(6)
$\left\{ {\begin{array}{*{20}{l}} {{{P}_{{n + 1}}} = a\min \left[ {{{F}_{n}},\,{{2{{F}_{n}}{{M}_{n}}} \mathord{\left/ {\vphantom {{2{{F}_{n}}{{M}_{n}}} {({{{{F}_{n}}} \mathord{\left/ {\vphantom {{{{F}_{n}}} h}} \right. \kern-0em} h} + {{M}_{n}})}}} \right. \kern-0em} {({{{{F}_{n}}} \mathord{\left/ {\vphantom {{{{F}_{n}}} h}} \right. \kern-0em} h} + {{M}_{n}})}}} \right],} \\ {{{F}_{{n + 1}}} = \delta \left[ {1 - \alpha {{P}_{n}} - \beta ({{F}_{n}} + {{M}_{n}})} \right]{{P}_{n}} + s{{F}_{n}},} \\ {{{M}_{{n + 1}}} = (1 - \delta )\left[ {1 - \alpha {{P}_{n}} - \beta ({{F}_{n}} + {{M}_{n}})} \right]{{P}_{n}} + {v}{{M}_{n}},} \end{array}} \right.$
где a – коэффициент рождаемости (среднее число потомков, приходящихся на одну брачную пару); δ – доля самок среди новорожденных; s и v – выживаемости половозрелых самок и самцов соответственно.

Потеря устойчивости равновесия системы (6) может происходить по сценариям Неймарка–Сакера и удвоения периода. С дальнейшим изменением модельных параметров возможен переход к хаотической динамике. Отметим, что наблюдаемые сложные бифуркации характерны и для других отображений, например трехмерного отображения Эно и его модификаций (Gonchenko, Gonchenko, 2016; Jiang et al., 2016; и др.). В параметрическом пространстве модели (6) имеются области мультистабильности. Фазовое пространство модели дробится бассейнами притяжений сосуществующих динамических режимов. В динамике реальных популяций “перескоки” по бассейнам соответствуют смене динамического режима, которая проявляется либо как изменение периода колебаний, либо как возникновение или исчезновение флуктуаций. Сосуществующие режимы возникают как в результате бифуркаций, так и вследствие переключения функции образования пар.

Исследование модели (6) выявило сложные связи между соотношением численностей полов и характером динамического поведения популяции (Ревуцкая и др., 2017). В популяциях, динамика которых может быть описана моделью (6), переходы между разными режимами возникают не только в результате изменений популяционных параметров, определяющих процессы воспроизводства и саморегуляции, но и в силу смены принципа образования пар. Выявленная мультистабильность позволяет заключить, что вариация численности популяции, ведущая к изменению отношения численностей полов, усложняет динамику популяции. При этом возникают трудности при идентификации типа наблюдаемого динамического режима, поскольку траектория формируется под воздействием процессов саморегуляции и смены типа образования пар, вызванной различием численностей полов.

СМЕНА РЕЖИМОВ ДИНАМИКИ В ПОПУЛЯЦИЯХ: ВЛИЯНИЕ МОДИФИЦИРУЮЩИХ ФАКТОРОВ

Влияние внешних факторов на циклическую динамику популяций – важное направление исследований в математической экологии. При этом анализируются не только закономерные колебания численности, но и явные переходы от одних динамических режимов к другим. Степень влияния внешних и внутрипопуляционных факторов не одинакова для различных видов растений и животных. Более того, она может значительно изменяться даже для одного и того же вида в зависимости от того, в какой природно-климатический зоне он обитает.

В рамках данного раздела, рассматривается ситуация, когда динамика популяции определяется как процессами авторегуляции, так и влиянием внешних факторов.

Влияние случайных факторов на динамику популяции с двумя возрастными классами. Применение модели (5) к описанию динамики популяции рыжей полевки Myodes glareolus на основе данных многолетних учетов на территории Удмуртского стационара (Жигальский, 2011) дало удовлетворительную аппроксимацию. Модельная траектория описывает тенденцию динамики, однако не полностью улавливает пики численности популяции рыжей полевки (Фрисман и др., 2015б). По-видимому, расхождение данных наблюдений и моделирования связано с влиянием внешних факторов.

Один из основных факторов, влияющих на репродуктивную активность многих грызунов, – запас кормовых ресурсов. Рост активности размножения при увеличении обилия корма носит “взрывной” характер. При прочих равных условиях этот процесс можно описать экспоненциальной функцией. Такой подход, в частности, был успешно применен для описания зависимости роста активности размножения маньчжурских белок при увеличении урожайности кедровых орехов (Ashichmina et al., 1985). Адекватных прямых оценок обилия кормов для рыжей полевки, по-видимому, не существует. Мы предлагаем использовать в качестве индикатора обилия кормовых запасов гидротермический коэффициент Селянинова (Sn), который характеризует влагообеспеченность территории. Внешний фактор позволил отловить основные пики численности популяции и улучшить адекватность модели. Это связано с тем, что коэффициенты, характеризующие репродуктивные потенциалы особей, не постоянны, их значения зависят от влагообеспеченности территории (рис. 5).

Рис. 5.

а – 1 и 2 – реальная и модельная годовая динамика популяции рыжей полевки соответственно; б – динамика относительных численностей сеголеток (x) – особей, рожденных в текущем году – и взрослых особей (y), а также средних значений гидротермического коэффициента Селянинова (S).

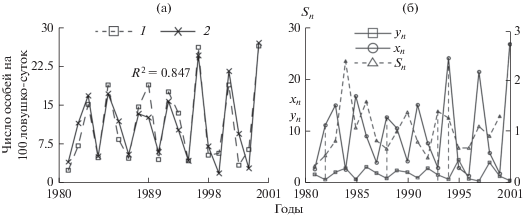
Дальнейшее исследование модели с двумя возрастными классами с учетом влияния климатических факторов на процессы воспроизводства показало, что численность популяции постоянно переходит из одного бассейна в другой и лишь в отдельные годы ненадолго задерживается в диапазоне значений параметров, при которых наблюдаются сходные режимы динамики (Neverova et al., 2019).

Влияние промыслового изъятия на динамику структурированной популяции. Влияние промыслового изъятия на динамику численности популяций рассмотрено многими исследователями (Ricker, 1954; Beverton, Holt, 1957; Beddington, May, 1977; Скалецкая и др., 1979; Абакумов, 1993; Lande et al., 1997; Braumann, 2002; Jensen, 2002; Runge, Johnson, 2002; Фрисман, Ласт, 2005; Ильин, 2007; Rolland et al., 2011; Wikstrom et al., 2012; Cid et al., 2014; Isomaa et al., 2014; Абакумов, Израильский, 2016; Segura et al., 2016; и др.). В большинстве случаев решались задачи оптимизации промыслового изъятия.

С проблемой рационального использования самовоспроизводящихся ресурсов одной из первых столкнулась ихтиология. В конце XIX в. было отмечено, что доля некоторых видов рыб (осетр, белуга, сазан, лещ, вобла и др.) в уловах стала уменьшаться с каждым годом. Следовательно, наибольшее развитие получили стратегии, ориентированные на оптимизацию промысла рыбных популяций (Баранов, 1918; Graham, 1935; Ricker, 1954; Schaefer, 1954; Beverton, Holt, 1957; Ricker, 1954; и др.).

Особое внимание было уделено задачам оптимизации промысла для моделей однородной популяции (Свирежев, Елизаров, 1972; Swan, 1975; Скалецкая и др., 1979; Абакумов, 1993). Вместе с тем научно обоснованная эксплуатация биологических ресурсов требует детального изучения их популяционной структуры (Свирежев, Елизаров, 1972; Beddington, Taylor, 1973; Колли, 1979; Скалецкая и др., 1979; Jensen, 1996; Langvatn, Loison, 1999). Во-первых, это обусловлено тем, что пополнение популяции – сложный процесс, включающий в себя не только рождаемость, но и выживаемость неполовозрелых особей, а также переходы младших особей в старшие возрастные классы и т.д.; на все эти процессы изменение плотности популяции и промысел оказывают различное влияние (Bergman et al., 2015). Во-вторых, в большинстве случаев экономически выгодно использовать дифференцированный промысел (Колли, 1979). Например, осетровые, сиговые и лососевые рыбы в зависимости от возраста имеют разную промысловую ценность (Фрисман, Ласт, 2005).

Наиболее известны две стратегии управления промыслом, при которых предполагается плотностная регуляция роста популяций. Первая стратегия основана на концепции ежегодных излишек урожая, вторая – на концепции максимального уравновешенного изъятия (Bergman et al., 2015). В ходе исследования динамики двухвозрастной эксплуатируемой популяции было показано, что максимальный устойчивый (оптимальный) промысел возможен при изъятии особей только из одного возрастного класса (Жданова, Фрисман, 2013; Ревуцкая, Фрисман, 2017).

Хорошо известно, что ведение промысла с оптимальной долей изъятия, обеспечивающей максимум равновесного урожая в однородной популяции (т.е. без учета возрастной структуры), приводит к стабилизации ее численности (Фрисман и др., 2003). Вместе с тем оказалось, что динамика эксплуатируемой популяции с возрастной структурой усложняется, если учесть тот факт, что особи разного возраста с различной степенью интенсивности влияют на процессы рождаемости или выживаемости. Было показано, что равновесный промысел из двухвозрастной популяции, основанный на стратегии изъятия с постоянной оптимальной долей, возможен в ограниченной области параметрического пространства, где стационарные решения устойчивы (Неверова и др., 2016, 2017; Ревуцкая, Фрисман, 2017). В случае потери устойчивости равновесной численности эта стратегия приводит к колебаниям и перестает быть как равновесной, так и оптимальной. Стабилизация динамики системы происходит при стратегии промысла, основанной на регулярном изъятии “излишка” численности над значением, соответствующим величине максимального воспроизводства популяции (Ревуцкая, Фрисман, 2017).

Стратегии, основанные на максимальном уравновешенном изъятии, могут привести к катастрофическим последствиям, вплоть до вырождения популяции (Larkin, 1977; Ludwig et al., 1993; Lande et al., 1995; Finley, 2011). Необратимые изменения в эксплуатируемых популяциях могут быть вызваны не только воздействием промысла, но и влиянием процессов саморегуляции в совокупности с факторами экзогенной природы, ведущими к вариации скорости роста популяции и, следовательно, к флуктуациям (Fryxell et al., 2010) или даже к смене динамического режима.

Отметим, что работы, в которых учитывается возможность мультистабильности в эксплуатируемых популяциях (Saucedo-Solorio et al., 2002; Pisarchik, Feudel, 2014; Фрисман и др., 2015б), встречаются достаточно редко. Однако такой подход позволяет изучать и учитывать возможность смены динамического режима в эксплуатируемой популяции. В частности, было показано, что для эксплуатируемой двухвозрастной популяции (как с учетом половой структуры, так и без него) сохраняется возможность реализации различных динамических режимов при одних и тех же значениях популяционных параметров в зависимости от начальной численности, характерная для свободно развивающейся популяции (Неверова и др., 2016, 2017; Ревуцкая и др., 2018; Neverova et al., 2018). Следовательно, чтобы стабилизировать динамику, необходимо текущую численность “удерживать” в бассейне притяжения интересующего режима, например, путем уменьшения численности одного из половозрастных классов. Вместе с тем возникают сложности при прогнозировании популяционной динамики, поскольку промысел может сместить текущую численность из одного бассейна притяжения в другой и привести к изменению типа динамики численности.

Влияние скорости восстановления ресурсов. Для изучения влияния скорости восстановления ресурсов на динамику популяции предлагается использовать модель Морана–Рикера с запаздыванием

(7)
${{x}_{{n + 1}}} = a{{x}_{n}}\exp \left( { - \sum\limits_{i = 0}^{i = m} {{{b}_{i}}{{x}_{{n - i}}}} } \right),$
где xn – численность популяции, с которой она вступает в n-й период размножения, а – репродуктивный потенциал популяции. Экспоненциальный множитель характеризует экологическое лимитирование роста численности популяции, m – значения временного лага, т.е. число поколений, в течение которых сказываются ограничения ресурсов жизнедеятельности.

При m = 0 уравнение (7) сводится к классической модели Рикера (Moran, 1950; Ricker, 1954), в которой предполагается, что каждое поколение “получает” одинаковый объем экологических ресурсов, необходимых для жизнедеятельности, независимо от предыдущей истории популяции. Это справедливо для тех видов, ресурсная база которых может полностью восстановиться за время между периодами размножения. При m = 1 предполагается, что ресурсы, необходимые для жизнедеятельности популяции, способны полностью восстановиться за время между двумя сезонами размножения. Уравнение (7) в этом случае принимает вид

(8)
${{x}_{{n + 1}}} = a{{x}_{n}}\exp ( - {{b}_{0}}{{x}_{n}} - {{b}_{1}}{{x}_{{n - 1}}}).$

Параметр b1 описывает уменьшение необходимых ресурсов, связанное с их потреблением предыдущим поколением. Уменьшение ресурсов может быть интерпретировано как эквивалентное уменьшение репродуктивного потенциала текущего поколения. Параметр b0 характеризует интенсивность плотностно-зависимого экологического лимитирования в условиях ограниченности ресурсов, приходящихся на одну особь популяции.

Исследование модели (7) при различных значениях лага показало, что вклад предыдущих поколений в экологическое лимитирование процессов воспроизводства приводит к усложнению динамики популяций (Neverova et al., 2016). В целом зависимость популяционной динамики от скорости восстановления ресурсов приводит к тому, что популяция в большинстве случаев демонстрирует квазипериодическую динамику. Двухлетние колебания возникают, когда ограничение роста численности осуществляется через плотностно-зависимую регуляцию в текущем году.

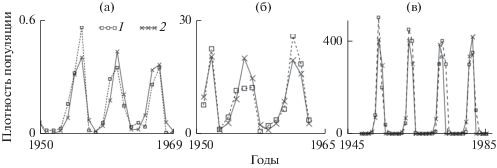
Модель Морана–Рикера при разных значениях лага применялась для описания динамики популяций насекомых (Neverova et al., 2016). На рис. 6 представлены результаты описания динамики популяций совки сосновой (Neverova et al., 2016), пяденицы сосновой (Neverova et al., 2016) и серой лиственничной листовертки (Sadykova, Nedorezov, 2013; Nedorezov, Sadykova, 2015) с помощью модели (8). Оценки параметров модели показывают, что во всех случаях b1 значительно больше b0 (ρ = b1/b0 больше 1), т.е. вклад предыдущего поколения в лимитирование воспроизводства популяции существенно больше вклада текущего поколения. Точечные оценки совки сосновой и пяденицы сосновой располагаются в области квазипериодических колебаний, где в случае небольших флуктуаций значений a и ρ характер динамики сохраняется. Вместе с тем есть возможность попадания параметров в зону одного из языков Арнольда и перехода от квазипериодической динамики к строго периодической. Точечная оценка параметров для серой лиственничной листовертки находится в окне периодичности, которое соответствует 18-летним колебаниям. Оценка параметров лежит вблизи границы, разделяющей 9- и 18-летние циклы, и флуктуация значений параметров может привести к смене динамического режима (Neverova et al., 2016).

Рис. 6.

Результаты описания динамики плотности насекомых моделью Морана–Рикера с лагом 1 год. а – совка сосновая Panolis flammea, б – пяденица сосновая Bupalus piniaria, в – серая лиственничная листовертка Zeiraphera diniana. 1 и 2 – реальные и модельные данные соответственно.

Влияние периодических изменений факторов внешней среды. Особый интерес представляет наличие периодических изменений факторов внешней среды, которые, в частности, могут приводить к периодическому изменению репродуктивного потенциала популяций с сезонным характером размножения. Подобная ситуация может быть описана с помощью уравнения Рикера с периодическим мальтузианским параметром, что позволяет учитывать циклические воздействия как экзогенной, так и эндогенной природы на численность популяции (Шлюфман и др., 2016, 2017, 2018; Фрисман и др., 2019). Исследование показало, что уравнение Рикера с мальтузианским параметром, меняющимся с периодом 2, наряду с мультистабильностью динамических режимов имеет и фазовую мультистабильность. В результате возмущения переменной или сдвига фазы мальтузианского параметра можно наблюдать сдвиг фазы колебаний или смену существующего режима. Модель имеет два разных устойчивых 2-летних цикла и две разные серии результатов их бифуркации по сценарию удвоения периода. Следовательно, 2-летние колебания численности в периодически изменяющейся среде могут быть как синхронны, так и асинхронны флуктуациям среды обитания.

ЗАКЛЮЧЕНИЕ

В современной биологии накопился колоссальный объем временны́х рядов эмпирических данных, свидетельствующих о том, что биологические системы обладают сложной динамикой. Наиболее яркий пример – исчезновение циклов в популяциях мелких млекопитающих, или же смена периода колебаний. Также могут наблюдаться различные динамические режимы в популяциях одного вида, которые обитают в максимально сходных условиях. Все эти явления вполне объясняются возможной мультистабильностью динамики природных популяций. Это приводит к необходимости проведения комплексных теоретических исследований динамики нелинейных систем и динамического хаоса в экологических системах. К настоящему времени получили развитие исследования сложной нерегулярной динамики физических, технических и математических систем, обнаружены такие особенности их динамики, как регулярные и хаотические колебания, бистабильность и мультистабильность, синхронизация и кластеризация и т.д.

Известно множество современных работ по математическому моделированию популяционной динамики. Традиционно для описания динамики природных систем используют непрерывные во времени модели. При этом важным этапом в понимании механизмов, вызывающих популяционные колебания, стало применение достаточно простых рекуррентных уравнений к изучению и моделированию динамики численности тех биологических видов, которые характеризуются четко выраженным сезоном размножения и стадийностью развития. Рекуррентные уравнения позволили объяснить резкие колебания численности популяций при сравнительно постоянных внешних условиях.

Оказалось, что периодические колебания, наблюдаемые в живых системах, могут определяться не только внешними воздействиями, но и внутренними свойствами самой популяционной системы. Кроме того, часто в экспериментальных и полевых исследованиях данные собираются регулярно в определенные интервалы времени, что также указывает на целесообразность использования рекуррентных уравнений.

В первой части обзора представлены методы и подходы к моделированию динамики популяций с использованием дискретных по времени моделей. Описана эволюция научных идей по пути усложнения дискретных во времени моделей – от модели Мальтуса до современных моделей, учитывающих разные факторы, влияющие на популяционную структуру и динамику численности, и отражающих большой спектр возможных динамических режимов. Рассмотрены динамические эффекты, к которым приводят плотностно-зависимая регуляция, усложнение возрастной и стадийной структур и влияние внешних факторов. Во второй части обзора будут рассмотрены динамические эффекты, возникающие в задачах моделирования процесса эволюции, а также влияния миграции на динамику популяций и особенности их пространственного распределения.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-14-50326.

Acknowledgments: The reported study was funded by RFBR, project number 19-14-50326.

Список литературы

  1. Абакумов А.И. Управление и оптимизация в моделях эксплуатируемых популяций. Владивосток: Дальнаука, 1993. 129 с.

  2. Абакумов А.И., Израильский Ю.Г. Эффекты промыслового воздействия на рыбную популяцию // Матем. биология и биоинформатика. 2016. Т. 11. № 2. С. 191–204.

  3. Баранов Ф.И. К вопросу о биологических основаниях рыбного хозяйства // Изв. отдела рыбоводства и науч.-промысл. исследований. 1918. Т. I. Вып. 2. С. 84–128.

  4. Гиммельфарб А.А., Гинзбург Л.Р., Полуэктов Р.А., Пых Ю.А., Ратнер В.А. Динамическая теория биологических популяций. М.: Наука, 1974. 456 с.

  5. Дажо Р. Основы экологии. М.: Прогресс, 1975. 416 с.

  6. Жданова О.Л., Фрисман Е.Я. Влияние оптимального промысла на характер динамики численности и генетического состава двухвозрастной популяции // Изв. РАН. Сер. биол. 2013. № 6. С. 738–749.

  7. Жигальский О.А. Структура популяционных циклов рыжей полевки (Myodes glareolus) в центре и на периферии ареала // Изв. РАН. Сер. биол. 2011. № 6. С. 733–746.

  8. Ильин О.И. Об оптимальной эксплуатации популяций рыб с возрастной структурой // Сиб. журн. индустр. математики. 2007. Т. 10. № 3. С. 43–57.

  9. Исаев А.С., Хлебопрос Р.Г., Недорезов Л.В., Киселев В.В., Кондаков Ю.П., Суховольский В.Г. Популяционная динамика лесных насекомых. М.: Наука, 2001. 347 с.

  10. Колли Г. Анализ популяций позвоночных. М.: Мир, 1979. 362 с.

  11. Кузнецов А.П., Савин А.В., Седова Ю.В., Тюрюкина Л.В. Бифуркации отображений. Саратов: Издат. центр “Наука”, 2012. 196 с.

  12. Логофет Д.О., Белова И.Н. Неотрицательные матрицы как инструмент моделирования динамики популяций: классические модели и современные обобщения // Фундам. и прикл. математика. 2007. Т. 13. № 4. С. 145–164.

  13. Логофет Д.О., Клочкова И.Н. Математика модели Лефковича: репродуктивный потенциал и асимптотические циклы // Матем. моделирование. 2002. Т. 14. №10. С. 116–126.

  14. Логофет Д.О., Белова И.Н., Казанцева Е.С., Онипченко В.Г. Ценопопуляция Незабудочника кавказского (Eritrichium caucasicum) как объект математического моделирования. I. Граф жизненного цикла и неавтономная матричная модель // Журн. общ. биологии. 2016. Т. 77. № 2. С. 106–121.

  15. Логофет Д.О. Казанцева Е.С., Белова И.Н, Онипченко В.Г. Ценопопуляция незабудочника кавказского (Eritrichium caucasicum) как объект математического моделирования. II. Сколько лет живет малолетник? // Журн. общ. биологии. 2017. Т. 78. № 1. С. 56–66.

  16. Неверова Г.П., Абакумов А.И., Фрисман Е.Я. Влияние промыслового изъятия на режимы динамики лимитированной популяции: результаты моделирования и численного исследования // Матем. биология и биоинформатика. 2016. Т. 11. № 1. С. 1–13.

  17. Неверова Г.П., Абакумов А.И., Фрисман Е.Я. Режимы динамики лимитированной структурированной популяции при избирательном промысле // Матем. биология и биоинформатика. 2017. Т. 12. № 2. С. 327–342.

  18. Недорезов Л.В. Моделирование вспышек массовых размножений насекомых. Новосибирск: Наука, 1986. 125 с.

  19. Недорезов Л.В. Анализ динамики численности сосновой пяденицы с помощью дискретных математических моделей // Матем. биология и биоинформатика. 2010. Т. 5. № 2. С. 114–123.

  20. Новиков Е.А., Панов В.В., Мошкин М.П. Плотностно-зависимые механизмы регуляции численности красной полевки (Myodes rutilus) в оптимальных и суботимальных местообитаниях юга Западной Сибири // Журн. общ. биологии. 2012. Т. 73. № 1. С. 49–58.

  21. Одум Ю. Основы экологии. М.: Мир, 1975. 741 с.

  22. Ревуцкая О.Л., Фрисман Е.Я. Влияние равновесного промысла на сценарии развития двухвозрастной популяции // Информатика и системы управления. 2017. №3 (53). С. 36–48.

  23. Ревуцкая О.Л., Неверова Г.П., Фрисман Е.Я. Влияние промыслового изъятия на динамику популяций с возрастной и половой структурой // Матем. биология и биоинформатика. 2018. Т. 13(1). С. 270–289.

  24. Ревуцкая О.Л., Кулаков М.П., Неверова Г.П., Фрисман Е.Я. Смена режимов в динамике численности популяции с возрастной и половой структурой // Докл. РАН. 2017. Т. 477. № 5. С. 622–627.

  25. Ревуцкая О.Л., Неверова Г.П., Кулаков М.П., Фрисман Е.Я. Модель динамики численности двухвозрастной популяции: устойчивость, мультистабильность и хаос // Нелинейная динамика. 2016. Т. 12. № 4. С. 591–603.

  26. Свирежев Ю.М., Елизаров Е.Я. Математическое моделирование биологических систем. М.: Наука, 1972. 158 с.

  27. Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.: Наука, 1978. 352 с.

  28. Скалецкая Е.И., Фрисман Е.Я., Шапиро А.П. Дискретные модели динамики численности популяций и оптимизация промысла. М.: Наука, 1979. С. 165.

  29. Тарасов М.В., Малышева Н.С., Самофалова Н.А., Елизаров А.С., Вагин Н.А. Применение дискретных моделей для прогнозирования популяционной динамики золотистой картофельной нематоды Globodera rostochiensis // Уч. записки: электрон. науч. журн. Курск. гос. ун-та. 2012. Т. 2. № 4 (24).

  30. Уильямсон М. Анализ биологических популяций / Перев. с англ. Базыкина А.Д. М.: Мир, 1975. 272 с.

  31. Фрисман Е.Я., Ласт Е.В. Нелинейные эффекты в популяционной динамике, связанные с возрастной структурой и влиянием промысла // Изв. РАН. Сер. биол. 2005. № 5. С. 517–530.

  32. Фрисман Е.Я., Ласт Е.В., Лазуткин А.Н. Механизмы и особенности сезонной и долговременной динамики популяций полевок Clethrionomys rufocanus и Cl. rutilus: количественный анализ и математическое моделирование // Вестн. Сев.-Вост. науч. центра ДВО РАН. 2010а. № 2. С. 43–47.

  33. Фрисман Е.Я., Ласт Е.В., Сычева Э.В. Динамическая неустойчивость в математических моделях динамики численности промысловых видов рыб. Препринт. Биробиджан: ИКАРП ДВО РАН, 2003. 54 с.

  34. Фрисман Е.Я., Неверова Г.П., Шлюфман К.В. Модельные динамические популяционные режимы в сообществах с циклирующими видами: синхронизация, параметрический резонанс и мультистабильность // Изв. РАН. Сер. биол. 2019. № 4. С. 341–352.

  35. Фрисман Е.Я., Ревуцкая О.Л., Неверова Г.П. Анализ популяционной динамики промысловых млекопитающих Среднего Приамурья России: математическое моделирование и оценка ресурсного потенциала. В: Биологические ресурсы Дальнего Востока: комплексный региональный проект ДВО РАН / Под ред. Журавлева Ю.Н. М.: КМК, 2007. С. 184–202.

  36. Фрисман Е.Я., Ревуцкая О.Л., Неверова Г.П. Сложные режимы динамики численности популяции с возрастной и половой структурой // Докл. РАН. 2010б. Т. 431. № 6. С. 844–848.

  37. Фрисман Е.Я., Ревуцкая О.Л., Неверова Г.П. Основные тенденции динамики численности промысловых млекопитающих Среднего Приамурья России: результаты наблюдений и моделирования // Сиб. лесн. журн. 2015а. № 3. С. 105–116.

  38. Фрисман Е.Я., Неверова Г.П., Кулаков М.П., Жигальский О.А. Явление мультирежимности в популяционной динамике животных с коротким жизненным циклом // Докл. РАН. 2015б. Т. 460. № 4. С. 488–493.

  39. Фрисман Е.Я., Неверова Г.П., Ревуцкая О.Л., Кулаков М.П. Режимы динамики модели двухвозрастной популяции // Изв. вузов ПНД. 2010в. Т. 18. № 2. С. 111–130. +

  40. Чернявский Ф.Б., Лазуткин А Н. Циклы леммингов и полевок на Севере. Магадан: ИБПС ДВО РАН, 2004. 150 с.

  41. Шапиро А.П. К вопросу о циклах в возвратных последовательностях // В: Управление и информация. Вып. 3. Владивосток: ДВНЦ АН СССР, 1972. С. 96–118.

  42. Шапиро А.П., Луппов С.П. Рекуррентные уравнения в теории популяционной биологии. М.: Наука, 1983. 132 с.

  43. Шлюфман К.В., Неверова Г.П., Фрисман Е.Я. Два циклы уравнения Рикера с периодически изменяющимся мальтузианским параметром: устойчивость и мультистабильность // Нелинейная динамика. 2016. Т. 12. № 4. С. 553–565.

  44. Шлюфман К.В., Неверова Г.П., Фрисман Е.Я. Динамические режимы модели Рикера с периодически изменяющимся мальтузианским параметром // Нелинейная динамика. 2017. Т. 13. № 3. С. 363–380.

  45. Шлюфман К.В., Неверова Г.П., Фрисман Е.Я. Фазовая мультистабильность колебательных режимов динамики модели Рикера с периодически изменяющимся мальтузианским параметром // Матем. биология и биоинформатика. 2018. Т. 13. № 1. С. 68–83.

  46. Шлюфман К.В., Фишман Б.Е., Фрисман Е.Я. Интервально-периодическая динамика рекуррентных уравнений // Информатика и системы управления. 2013. Т. 37. № 3. С. 66–73.

  47. Ashichmina E.V., Frisman E.Ya. Skaletskaya E.I., Kulikov A.N. Mathematical model for dynamics of the number of pelt products from the local population of Mantchurian squirrels // Ecol. Mod. 1985. V. 30. P. 145–156.

  48. Barraquand F., Louca S., Abbott K.C., Cobbold C.A., Cordoleani F., DeAngelis D.L., Elderd B.D., Fox J.W., Greenwood P., Hilker F.M., Murray D.L., Stieha C.R., Taylor R.A., Vitense K., Wolkowicz G.S.K., Tyson R.C. Moving forward in circles: challenges and opportunities in modelling population cycles // Ecol. Lett. 2017. V. 20. № 8. P. 1074–1092.

  49. Bechtol W.R., Kruse G.H. Analysis of a stock-recruit relationship for red king crab off Kodiak Island, Alaska // Marine and Coastal Fisheries: Dynamics, Management, and Ecosystem Science. 2009. V. 1. P. 29–44.

  50. Beddington J.R., May R.M. Harvesting populations in a randomly fluctuating environment // Science. 1977. V. 197. P. 463–465.

  51. Beddington J.R., Taylor D.B. Optimal age specific harvesting of a population // Biometrics. 1973. V. 29. P. 801–809.

  52. Bergman E.J., Doherty P.F., White G.C., Holland A.A. Density dependence in mule deer: a review of evidence // Wildlife Biol. 2015. V. 21(1). P. 18–29.

  53. Berryman A.A., Turchin P. Identifying the density-dependent structure underlying ecological time series // Oikos. 2001. V. 92. P. 265–270.

  54. Bessa-Gomes C., Legendre S., Clobert J. Discrete two-sex models of population dynamics: On modeling the mating function // Acta Oecol. 2010. V. 36. P. 439–445.

  55. Beverton R.J.H., Holt S.J. On the dynamics of exploited fish populations. United Kingdom Ministry of Agriculture, Food, and Fisheries Investigations, 1957. Ser. 2, 19. 533 p.

  56. Boer P.J., Reddingius J. Regulation and stabilization paradigms in population ecology. Netherlands: Chapman & Hall Ltd., 1996. 400 p.

  57. Braumann C.A. Variable effort harvesting models in random environments: generalization to density-dependent noise intensities // Math. Biosc. 2002. V. 177–178. P. 229–245.

  58. Caswell H. Matrix Population Models: construction, analysis, and interpretation. Massachusetts: Sinauer Assoc. Ink., 2001. 722 p.

  59. Caswell H., Weeks D.E. Two-sex models: chaos, extinction, and other dynamic consequences of sex // Am. Nat. 1986. V. 128. P. 707–735.

  60. Cid B., Hilker F.M., Liz E. Harvest timing and its population dynamic consequences in a discrete single-species model // Math. Biosc. 2014. V. 248. P. 78–87.

  61. Cornulier T., Yoccoz N.G., Bretagnolle V., Brommer J.E., Butet A., Ecke F., Elston D.A., Framstad E., Henttonen H., Hörnfeldt B. Europe – wide dampening of population cycles in keystone herbivores // Science. 2013. V. 340. P. 63–66.

  62. Coulson T., Malo A. Case of absent lemmings // Nature. 2008. V. 456. P. 43–44.

  63. Dennis B., Taper M.L. Density dependence in time series observations of natural populations: estimation and testing // Ecol. Monogr. 1994. V. 64(2). P. 205–224.

  64. Feigenbaum M.J. Universal behavior in nonlinear systems // Phys. D: Nonlinear Phenomena. 1983. V. 7. № 1–3. P. 16–39.

  65. Finley P. All the fish in the sea: maximum sustainable yield and the failure of fisheries management. Chicago: Univ. Chicago Press, 2011. 210 p.

  66. Fisher R.A. The genetical theory of natural selection. Oxford: Clarendon Press, 1930. 272 p.

  67. Frisman E.Y., Neverova G.P., Kulakov M.P. Change of dynamic regimes in the population of species with short life cycles: Results of an analytical and numerical study // Ecol. Complexity. 2016. V. 27. P. 2–11.

  68. Frisman E.Ya., Neverova G.P., Revutskaya O.L. Complex dynamics of the population with a simple age structure // Ecol. Modell. 2011. V. 222. P. 1943–1950.

  69. Frisman E.Ya., Skaletskaya E.I., Kuzyn A.E. A mathematical model of the population dynamics of a local northern fur seal with seal herd // Ecol. Modell. 1982. V. 16. P. 151–172.

  70. Fryxell J.M., Packer P., McCann K., Solberg E.J., Sæther B.E. Resource management cycles and the sustainability of harvested wildlife populations // Science. 2010. V. 328. Iss. 5980. P. 903–906.

  71. Gerber L.R., White E.R. Two-sex matrix models in assessing population viability: when do male dynamics matter? // J. Appl. Ecol. 2014. V. 51. P. 270–278.

  72. Ginzburg L., Colyvan M. Ecological Orbits: How Planets Move And Populations Grow. N.Y.: Oxford Univ. Press, 2004. 184 p.

  73. Gonchenko A.S., Gonchenko S.V. Variety of strange pseudohyperbolic attractors in three-dimensional generalized Hénon maps // Physica D. 2016. V. 337. P. 43–57.

  74. Graham M. Modern theory of exploiting a fishery and applications to North Sea trawling // J. Cons. Int. Explor. Mer. 1935. V. 10. P. 264–274.

  75. Gurney W., Nisbet R. Ecological dynamics. N.Y.: Oxford Univ. Press, 1998. 352 p.

  76. Haldane J.B.S. A mathematical theory of natural and artificial selection. P. 1 // Trans. Cambr. Philos. Soc. 1924. V. 23. P. 19–41.

  77. Hassell M.P. Density-dependence in single-species population // J. Animal. Ecol. 1975. V. 45. № 1. P. 283–294.

  78. Henson S.M., Cushing J.M, Costantino R.F., Dennis B., Desharnais R.A. Phase switching in population cycles // Proc. R. Soc. Lond. B. 1998. V. 265. P. 2229–2234.

  79. Henttonen H., Wallgren H. Small rodent dynamics and communities in the birch forest zone of northern Fennoscandia // Nordic Mountain Birch Ecosystems / Ed. Wielgolaski F.E. N.Y.: Parthenon, 2001. P. 262–278.

  80. Inchausti P., Ginzburg L.R. Small mammals cycles in northern Europe: patterns and evidence for the maternal effect hypothesis // J. Anim. Ecol. 1998. V. 67. P. 180–194.

  81. Isomaa M., Kaitala V., Laakso J. Determining the impact of initial age structure on the recovery of a healthy over-harvested population // Ecol. Modell. 2014. V. 286. P. 45–52.

  82. Jensen A.L. Density-dependent matrix yield equation for optimal harvest of age-structured wildlife populations // Ecol. Modell. 1996. № 88. P. 125–132.

  83. Jensen A.L. Analysis of harvest and effort data for wild populations in fluctuating environments // Ecol. Modell. 2002. V. 157. P. 43–49.

  84. Jiang H., Liu Y., Wei Z., Zhang L. A new class of three-dimensional maps with hidden chaotic dynamics // Inter. J. Bifurc. Chaos. 2016. V. 26. № 12. 1650206 (13 p.).

  85. Kausrud K.L., Mysterud A., Steen H., Vik J.O., Østbye E., Cazelles B., Framstad E., Eikeset A.M., Mysterud I., Solhøy T., Stenseth N.C. Linking climate change to lemming cycles // Nature. 2008. V. 456. P. 93–97.

  86. Kendall B.E., Briggs C.J., Murdoch W.W., Turchin P., Ellner S.P., McCauley E., Nisbet R.M., Wood S.N. Why do population cycle? A synthesis of statistical and mechanistic modeling approaches // Ecology. 1999. V. 80. P. 1789–1805.

  87. Kostitzin V.A. La biologie mathematique. Paris: A. Colin, 1937. 236 p.

  88. Krebs P.J. Population Fluctuations in Rodents. Chicago: Univ. Chicago Press, 2013. 320 p.

  89. Lack D. The natural regulation of animal numbers. N.Y.: Oxford Univ. Press, 1954. 343 p.

  90. Lande R., Engen S., Saether B.E. Optimal harvesting of fluctuating populations with a risk of extinction // Amer. Natur. 1995. V. 145. № 5. P. 728–745.

  91. Lande R., Saether B.-E., Engen S. Threshold harvesting for sustainability of fluctuating resources // Ecology. 1997. V. 78. P. 1341–1350.

  92. Langvatn R., Loison A. Consequences of harvesting on age structure, sex ratio and population dynamics of red deer Cervus elaphus in central Norway // Wildlife Biol. 1999. V. 5. № 4. P. 213–223.

  93. Larkin P.A. An epitaph for the concept of maximum sustained yield // Transact. Amer. Fisher. Soc. 1977. V. 106. № 1. P. 1–11.

  94. Lefkovitch L.P. The study of population growth in organisms grouped by stages // Biometrics. 1965. V. 21. P. 1–18.

  95. Leslie P.H. On the use of matrices in certain population mathematics // Biometrika. 1945. V. 33. P. 183–212.

  96. indstrom J., Kokko H. Sexual reproduction and population dynamics: the role of polygyny and demographic sex differences // Proc. R. Soc. Lond. B. 1998. V. 265. P. 483–488

  97. Logofet D.O. Convexity in projection matrices: projection to a calibration problem // Ecol. Modell. 2008. V. 216. № 2. P. 217–228.

  98. Logofet D.O. Does averaging overestimate or underestimate population growth? It depends // Ecol. Modell. 2019. V. 411. P. 108744.

  99. Logofet D.O., Kazantseva E.S., Belova I.N., Onipchenko V.G. Local population of Eritrichium caucasicum as an object of mathematical modelling. II. How short does the short-lived perennial live? // Biol. Bull. Rev. 2018. V. 8(3). P. 193–202.

  100. Logofet D.O., Ulanova N.G., Klochkova I.N., Demidova A.N. Structure and dynamics of a clonal plant population: Classical model results in a non-classic formulation // Ecol. Modell. 2006. V. 192. № 1–2. P. 95–106.

  101. Lotka A.J. Elements of physical bioloqy. Baltimor: Williams and Wilkins, 1925. 495 p.

  102. Ludwig D., Hilborn R., Walters P. Uncertainty, resource exploitation, and conservation: lessons from history // Ecol. Appl. 1993. V. 3. № 4. P. 547–549.

  103. May R.M. Biological population obeying difference equations: stable points, stable cycles, and chaos // J. Theor. Biol. 1975. V. 51. № 2. P. 511–524.

  104. Miller T.E.X., Inouye B.D. Confronting two-sex demographic models with data // Ecology. 2011. V. 92. P. 2141–2151.

  105. Molnar P.K., Derocher A.E., Lewis M.A., Taylor M.K. Modelling the mating system of polar bears: a mechanistic approach to the Allee effect // Proc. R. Soc. B. 2008. V. 275. P. 217–226.

  106. Moran P.A.P. Some remarks on animal population dynamics // Biometrics. 1950. V. 6(3). P. 250–258.

  107. Myers R.A., Bowen K.G., Barrowman N.J. Maximum reproductive Aquatic Sciences rate of fish at low population sizes // Can. J. Fish. 1999. V. 56(12). P. 2404–2419.

  108. Nedorezov L.V. Chaos and order in population dynamics: modeling, analysis, forecast. Saarbrucken: LAP Lambert Acad. Publ., 2012. 352 p.

  109. Nedorezov L.V., Sadykova D.L. Green oak leaf roller moth dynamics: An application of discrete time mathematical models // Ecol. Modell. 2008. V. 212(1). P.162–170.

  110. Nedorezov L.V., Sadykova D.L. Dynamics of larch bud moth populations: application of Moran-Ricker models with time lag // Ecol. Modell. 2015. V. 297. P. 26–32.

  111. Neverova G.P., Kulakov M.P, Frisman E.Ya. Changes in population dynamics regimes as result of both multistability and climatic fluctuation // Nonlinear dynamics. 2019. V. 97. № 1. P. 107–122.

  112. Neverova G.P., Yarovenko I.P., Frisman E.Y. Dynamics of populations with delayed density dependent birth rate regulation // Ecol. Modell. 2016. V. 340. P. 64–73.

  113. Neverova G.P., Abakumov A.I., Yarovenko I.P., Frisman E.Ya. Mode change in the dynamics of exploited limited population with age structure // Nonlinear Dynam. 2018. V. 94. P. 827–844.

  114. Pisarchik A.N., Feudel U. Control of multistability // Phys. Repts. 2014. V. 540. P. 167–218.

  115. Prout T., McChesney F. Competition among immatures affects their adult fertility: population dynamics // Amer. Natur. 1985. V. 126. № 4. P. 521–558.

  116. Revutskaya O., Neverova G., Frisman E. Complex dynamic modes in a two-sex age-structured population model // Models of the ecological hierarchy: from molecules to the ecosphere / Eds Jordán F., Jørgensen S.E. Elsevier, 2012. P. 149–162.

  117. Ricker W.E. Stock and recruitment // J. Fish. Res. Board Can. 1954. V. 11(5). P. 559–623.

  118. Rolland V., Hostetler J.A., Hines T.C., Johnson F.A. Percival H.F., Oli M.K. Effects of harvest and climate on population dynamics of northern bobwhites in south Florida // Wildlife Res. 2011. V. 38. P. 396–407.

  119. Romera M., Banuls V., Pastor G., Alvarez G., Montoya F. Snail-like pattern generation with the Hénon family of maps // Computers Graphics. 2001. V. 25. P. 529–537.

  120. Runge M.C., Johnson F.A. The importance of functional form in optimal control solutions of problems in population dynamics // Ecology. 2002. V. 83. № 5. P. 1357–1371.

  121. Sadykova D.L., Nedorezov L.V. Larch bud moth dynamics: can we explain periodicity of population fluctuations by the time lag dependence in birth rate? // Popul. Dynam.: Analysis, Modell., Forecast. 2013. V. 2(4). P. 154–181.

  122. Saucedo-Solorio J.M, Pisarchik A.N., Aboites V. Shift of critical points in the parametrically modulated Hénon map with coexisting attractors // Phys. Lett. 2002. V. A 304. P. 21–29.

  123. Schaefer M.B. Some aspects of dynamics of populations important to the management of commercial marine fisheries // Inter. Amer. Trop. Tuna Comm. Bull. 1954. V. 1. P. 27–56.

  124. Segura J., Hilker F.M., Franco D. Adaptive threshold harvesting and the suppression of transients // J. Theoret. Biol. 2016. V. 395. P. 103–114.

  125. Shrimali M.D., Prasad A., Ramaswamy R., Feudel U. The nature of attractors basins in multistable systems // Inter. J. Bif. Chaos. 2008. V. 18. № 6. P. 1675–1688.

  126. Shyu E., Caswell H. Frequency-dependent two-sex models: a new approach to sex ratio evolution with multiple maternal conditions // Ecol. Evol. 2016. V. 6(19). P. 6855–6879.

  127. Swan G.W. Some strategies for harvesting a single species // Bull. Math. Biol. 1975. V. 37. P. 659–673.

  128. Turchin P. Rarity of density dependence or population regulation with lags? // Nature. 1990. V. 344. P. 660–663.

  129. Turchin P. Complex population dynamics: a theoretical / empirical synthesis. Princeton: Princeton Univ. Press, 2003. 472 p.

  130. Turchin P., Wood S.N., Ellner S.P., Kendall B.E., Murdoch W.W., Fischlin A., Casas J., McCauley E., Briggs C.J. Dynamical effects of plant quality and parasitism on population cycles of larch budmoth // Ecology. 2003. V. 84(5). P. 1207–1214.

  131. Volterra V. Lecons sur la theorie mathematique de la lutte pour la vie. Paris: Gauthier-Villars, 1931. 220 p.

  132. White T.C.R. What has stopped the cycles of sub-Arctic animal populations? Predators or food? // Basic Appl. Ecol. 2011. V. 12. P. 481–487.

  133. Wikstrom A., Ripa J., Jonzen N. The role of harvesting in age-structured populations: Disentangling dynamic and age truncation effects // Theor. Populat. Biol. 2012. V. 82. P. 348–354.

  134. Williams D.W., Liebhold A. Detection of delayed density dependence: effects of autocorrelation in an exogenous factor // Ecology. 1995. V. 76. № 3. P. 1005–1008.

  135. Wright S. Evolution in Mendelian populations // Genetics. 1931. V. 16. P. 97–159.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Серия биологическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал