Известия РАН. Серия биологическая, 2023, № 7-suppl, стр. 93-108

ВВЕДЕНИЕ

Проблема реальности границ является предметом дискуссии на протяжении двухсот лет с начала формирования географии как науки. В конце 18 в. было уже общепринятым рассматривать все явления природы (неорганические, органические, социальные), как функциональные отношения частей единого целого. Идея целостности могла выражаться и в особенностях каждой конкретной области. Так Бьютт (Butte), в 1811 утверждал: “никакой ученый не сомневается относительно существования земного организма” (цит. по Hartshorne, 1939). Для Бьютта индивидуальные страны и районы были “организмы”, которые подобно любому организму, включали физическую и психическую сущности, основой последней был человек. Однако, как всегда в науке существовало и прямо противоположное видение реальности. Противники гиперцелостности обращали внимание на тот факт, что трудно найти регионы, которые обособлялись бы границами одновременно всех явлений. Наиболее полная критика этой “целостной” концепции была дана А.Л. Бучером (Bucher) в 1827 г. В конечном итоге, он пришел к выводу, что нет необходимости изучать границы, регионы могут быть выделены любым произвольным способом. Он доказывал, что география должна изучать отношения конкретных явлений на любом участке земной поверхности (цит. по Hartshorne, 1939).

Наиболее остро вопрос о целостности стоял для биотической составляющей ландшафта – растительного покрова. В начале XX в. Морозов (1913, 1928) и Клементс (Clements, 1905, 1936) независимо друг от друга воспринимали растительные сообщества как отдельные организмы. Глизон (1917, 1939) и Раменский (1924) сформулировали гипотезу непрерывности растительного покрова. Особенно полно она была доказана в работах Раменского (1910, 1924) с обширным статистическим материалом. Раменский писал, что, хотя выделение границ и возможно, но они априори условны. В фитоценологии и геоботанике организменная концепция господствовала вплоть до 1960 г. Результаты исследований Уитеккера (Whittaker, 1956, 1960) в Центральных Аппалачах убедительно подтвердили представления Раменского и Глизона, практически все мировое научное сообщество геоботаников очень быстро признало индивидуалистическую концепцию и, соответственно, непрерывность растительного покрова, практически полностью отрицая реализуемость организменной концепции. Истинность при определенных условиях реализации индивидуалистической концепции была строго доказана в рамках математической теории устойчивости и подтверждена в прямых полевых исследованиях с применением различных статистических методов ординации (Пузаченко, 2004). Однако в конце XX–начале XXI века абсолютная общность индивидуалистической концепции была поставлена под сомнение (Пузаченко, 2017). Это, в частности, привело к новому всплеску интереса к границам, целостности и исследованию их природы.

Аналогичные проблемы соотношения целостности и непрерывности существуют в почвоведении и ландшафтоведении, но они менее разработаны. Так в почвоведении педон мыслится как материальное тело с линейными размерами от одного до десяти метров, но большинство почвоведов рассматривают почвенный покров в целом или в отдельных его свойствах как непрерывный. В ландшафтоведении Д.Л. Арманд (1975) доказывал непрерывность ландшафта и условность выделяемых границ. С другой стороны, школа ландшафтоведения, наследующая идеи Солнцева, не высказывает никаких сомнений в объективности их существования. Следует отметить, что практика планирования использования природных ресурсов требует обязательного введения территориальных единиц с их границами.

Обратим внимание на тот факт, что индивидуалистические и организменные отношения вполне совместимы в реальной системе. Индивидуалистическая концепция по условию отражает равновесные (стационарные) отношения между элементами системы. Статистические методы, используемые для многомерного анализа отношений, сами по себе выделяют только равновесные отношения. Вклад этих отношений можно оценить по коэффициенту детерминации варьирования в пространстве значения каждого элемента от осей или факторов, выделенных в многомерном анализе. Однако, если коэффициент детерминации очень велик, то это совершенно не значит, что отношения равновесны и нет нарушающих его организменно-подобных образований. Для доказательства равновесия необходимо, чтобы остатки от статистической модели каждого элемента имели бы строго нормальное распределение и нулевую автокорреляцию ряда. Обычно этого не бывает и существуют интервалы в пространстве, имеющие не менее четырех соседствующих точек с одним знаком отклонения от равновесной модели (Пузаченко, 2017). Необходимо обратить внимание на то, что проблема выделения границ и их реальности рассматриваются также при анализе пространственной структуры популяций (Ranke et al., 2021), в экономической географии (Gallaway, 2005; Колосов и др., 2014) и других областях, так или иначе касающихся явлений, имеющих пространственную дифференциацию.

В настоящем сообщении на основе теории информации и фундаментальной теоремы отсчета Котельникова в частности предлагается методология выделения и описания границ природных объектов, как функции частоты опробования в пространственном ряду с регулярным шагом опробования. Предлагается ввести для пространства единицу измерения “берг” – одно полное колебание на один километр, по сути тождественную единице “герц” для временного ряда. Кратко рассматриваются четыре основные модели возникновения границ и, в частном случае целостности, вытекающие из теории нелинейных динамических систем. Основные положения методологии иллюстрируются на реальных измерениях свойств биогеоценозов и измерениях отраженной солнечной радиации в каналах спутника SPOT 6. В предложенной постановке проблемы общие теоретические представления о неравновесных, нелинейных, динамических системах тесно взаимодействуют с представлениями классического натуралиста, объединяя их для ответа на фундаментальные вопросы: почему существуют конкретные пространственно-временные структуры и каковы пути их эволюции. Отвечая на эти вопросы, мы ищем порождающие их физические механизмы, последовательно совершенствуя соответствующие модели.

ТЕОРИЯ ИНФОРМАЦИИ В ИССЛЕДОВАНИИ ПЕРЕХОДНЫХ ЗОН

Рассматривая постановку проблемы границ в ландшафтной экологии нельзя не отметить практически полное игнорирование для ее решения хорошо развитой и в своих основаниях строго доказанной теории передачи информации во времени по каналам связи любой физической природы (Shannon, 1949). Частоты флюктуации переменных любой физической природы измеряются в непрерывной шкале с единицей измерения одно полное колебание в секунду (герц), что обеспечивает их полную непрерывность и соизмеримость. Надо полагать, что тоже самое справедливо и для пространственных флюктуаций. Соответственно, наша задача показать связь неопределенности при выделении резких и постепенных границ с полосой частот, реализованных в конкретных измерениях, и предложить метод ее снижения для реальных исследований структуры переходных зон и выделения возможно целостных систем с резкими границами. Однако, теоретическая основа для исследования пространственной структуры на основе трансектов с регулярным шагом опробования и дистанционной информации с заданным максимальным разрешением является общей.

В теории информации сформулированы общие законы передачи информации, справедливые для систем любой физической реализации (Шеннон, 1963). В общем случае, допускается, что существует передатчик (в широком смысле среда) который генерирует во времени колебания всех своих свойств или иначе ведет себя как динамическая система. Приемник в данном случае – исследователь, который с помощью некоторой измерительной системы пытается воспроизвести варьирование отдельно взятых свойств. Естественно, что для каждого свойства есть специфический приемник, который воспроизводит сигнал, поступающий из среды через равные промежутки времени. Возникает вопрос: каковы должны быть эти равные промежутки и каково должно быть время приема информации, чтобы полностью, без искажения, воспроизвести функцию, отражающую поведение рассматриваемого свойства во времени? Эта задача была решена В.А. Котельниковым (1933), в настоящее время называемой теоремой отсчета и лежащей в основе закона о пропускной способности канала связи K. Шеннона (Shannon, 1949).

Теорема отсчета доказывает, что 1) Если функция не содержит частот выше W герц, она полностью определяется своими мгновенными значениями в моменты, отстоящие друг от друга на 1/(2W) с. 2) Функция полностью определяется своими мгновенными значениями, если не содержит частот ниже W₁ герц и выше W₂ герц. 3) Функция полностью определяется своими мгновенными значения, если требует передачи длиной меньше Т условных единиц c частотой f_min < 2/T и шаг (расстояние) между отсчетами nΔt (f_max = = 1/2nΔt), при n = 1 (каждый последовательный отсчет) f_max = 0.5 (частота Найквиста). Для любых колебаний любых переменных во времени введена единая единица измерения частоты – герц, или одно колебание в с. При этом отсчеты могут браться через секунду, через 0.1 с и вообще с любым временным шагом. Теорема утверждает, что функция полностью воспроизводима по наблюдениям, если она не содержит частот выше некоторой величины, и, соответственно, не воспроизводима, если содержит их при отсчетах, отстоящих друг от друга на минимально возможный в данной системе измерения временной интервал. Вторая запись теоремы определяет воспроизводилось функции в полосе частот W₂–W₁. Третья запись представляет время в безразмерных единицах, и минимальная частота определяется временем измерения, а максимальная удвоенным регулярным интервалом. Когда интервал равен в условных единицах одному шагу, то частота максимальна и равна 0.5. Это безразмерная форма обычно используется во всех статистических пакетах анализа временных рядов. Обратим внимание, что введение общей единицы частоты “герц” позволяет сопоставлять и сравнивать любые измерения, осуществленные во времени.

При переходе к пространственным рядам все положения о воспроизводимой в измерениях внешней переменной остаются те же и к анализу пространственных рядов полностью применима вся мощная теория анализа временных рядов. В системах измерения отраженной солнечной радиации со спутников минимальная пространственная частота задается размером пикселя, а максимальная – половиной длины ряда по соответствующей координате. Как и для времени, для пространства можно ввести частоту в условных единицах. Но это неудобно, так как затрудняет сравнение независимых измерений, выполненных при разном шаге опробования или при разном разрешении космических снимков. В целом, возможность применения теоремы отсчета к пространственным рядам была показана (Пузаченко, 1976, 1983). Им было предложено осуществлять измерение разнообразия всех свойств ландшафта на трансектах с регулярным шагом опробования, и предложена единица пространственной частоты “берг”, равная одному полному колебанию на один километр. Таким образом, если, например, мы говорим – частота колебания 100 берг, то это означает, что в среднем, на один км воспроизводимо сто колебаний, если конечно таковые существуют. Выбор в названии единицы фамилии Л.С. Берга для русскоязычных географов очевиден, а выбор в качестве единицы 1 км, соответствует представлениям о том, что ландшафт в понимании школы Н.А. Солнцева, не должен иметь меньшие линейные размеры. Идея строго линейного трансекта с регулярным шагом опробования была в полной мере реализована при исследовании разнообразия ландшафта малых островов в юго-западной части Тихого океана (Puzachenko, 1994).

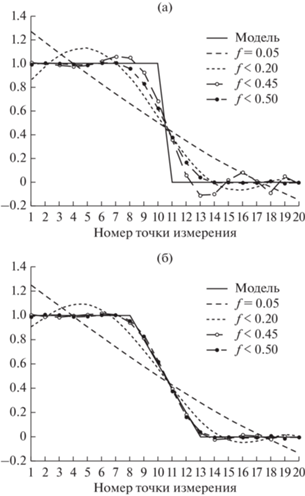
Рассмотрим возможность идентификации типа границ с использованием теоремы отсчета на двух простых модельных примерах (рис. 1). Зададим интервал измерения по регулярной схеме длиной в двадцать точек. Расстояние или время в данном случае задано в условных единицах. На рис. 1а задана резкая граница (грань), а на рис. 1б постепенная. Покажем, как аппроксимируется модельный ряд при различных полосах частот, т.е. шаге опробования. Первая частота по данному ряду составляет f₁ = 0.05, и шаг (расстояние) между отсчетами составляет n = 1/2f, т.е. 10 точек заданного ряда. Как следует из рис. 1, при этой частоте вся заданная область отражается как континуальная граница. Зададим следующую частоту ${{f}_{2}} \leqslant 0.2,$ что соответствует расстоянию 2.5 точек. Заданная модель границы описывается практически синусоидой. При f < 0.45 шаг между отсчетами составляет 1.111 и при f < 0.5 – измерения осуществляются в каждой точке и заданная резкая граница описывается практически полностью (рис. 1a) На рис. 1б, аналогичные расчеты приведены для постепенной границы. Как следует из рисунка, при максимальной частоте опробования получаем точное описание переходной зоны. Таким образом, если мы исследуем некоторую граничную область какого-либо свойства в природе, то постоянное увеличение “крутизны” аппроксимирующей линии с ростом частоты опробования индицирует существование резкой границы. В противном случае при максимальной частоте опробования однозначно выделяется переходная зона.

Рис. 1.

Отображение структуры границы для двух моделей через непрерывную функцию Фурье: а – резкая, б – постепенная.

Можно предложить другой, безусловно, более удобный метод идентификации типа границы. Рассмотрим квадрат расстояния значений переменной между соседними токами через две, три, четыре и т.д. точки, имитируя изменение шага измерения переменной ${{D}_{{i = 1,2,3,...n - {\text{step}}}}} = {{\left( {y_{i}^{2} - y_{{i + k}}^{2}} \right)}^{2}}.$ Как следует из рис. 2, если граница при максимальной частоте измерения дискретная, то при разном шаге измерения она будет давать одно и то же значение дистанции, лишь смещаясь по оси Х на один шаг (рис. 2а). Если граница постепенная (рис. 2б), то при расчете для соседних точек измерения получаем постепенное изменение дистанции. При изменении шага дистанции становятся более контрастными, и при измерении через четыре точки граница становится резкой с единственной достоверной дистанцией. Таким образом, получаем, что резкая граница при одной частоте измерений может быть переходной при увеличении частоты, формально доказать, что граница резкая на всех возможных интервалах измерения во времени или пространстве невозможно. Таким образом, при измерении реальных объектов, всегда необходимо указывать для какой частоты мы получаем резкую границу.

Рис. 2.

Отображение структуры границы для двух моделей через изменение шага взятия отсчета. а – резкая, б – постепенная.

Очевидно, что те же результаты получим, если будем рассматривать значения переменной при разном шаге опробования не в отдельных точках, а по осредненным по двум, трем, четырем и т.д. точкам, что в частности, более удобно при работе с дистанционной информацией. Для обеспечения сравнимости различных независимых измерений, осуществленных в разных масштабах, перейдем к пространственным частотам (берг). Если наши наблюдения осуществляются с шагом в один метр, то максимальная частота будет 500 берг или пятьсот полных колебаний на один км. Исходя из этого соотношения, легко перевести расчеты, выполненные в условных единицах в единицу пространственной частоты.

КЛАССИЧЕСКИЕ МОДЕЛИ, ПОРОЖДАЮЩИЕ РАЗЛИЧНЫЕ ТИПЫ ГРАНИЦ И ФОРМИРОВАНИЕ ЦЕЛОСТНЫХ ПРИРОДНЫХ СИСТЕМ

Выделение разных типов границ представляет мало интереса, если не осуществляет поиска ответа на вопрос о порождающих их механизмах. В общем случае, очевидно, что в большинстве случаев границы выделяют области неравновесных преобразований геосистем в пространстве. Особый интерес представляют природные системы, ограниченные резкими границами. Возможно, они выделяют целостные организменно-подобные образования, по условию обладающие повышенной устойчивостью в широком диапазоне изменения условий среды. На первый взгляд может показаться, что идентификация генезиса границ представляется трудно разрешимой, но теория нелинейной динамики предлагает строго ограниченный перечень и для каждой модели можно предложить критерии их идентификации в природе.

Модель бифуркации. Многие отношения в природе описываются моделями второй или третьей степени:

где X – внешняя переменная, a_max и a_min левая и правая границы области существования Y, α и β коэффициенты, описывающие ассиметричные параболы (Kuznetsov, 1998).

Такая модель обычно описывает экологические ниши видов по одному фактору (X) среды (Пузаченко, 1996). Эта модель часто хорошо объясняет переходные зоны различной структуры между растительными сообществами. Основным условием для их реализации является постепенное изменение условий среды обычно на наклонной поверхности рельефа, определяющего градиент увлажнения и минерального питания. Граница может быть более резкой при смене почвообразующих пород. При этом имеем в виду, что каждый вид зависит не от одного, а от четырех–пяти внешних факторов и по каждому фактору существуют свои потенциальные точки бифуркации. В соответствии с континуальной моделью, виды могут быть независимы друг от друга, однако, если у некоторых видов по какому-либо фактору точки бифуркации близки, то они одновременно сменяются экологически замещающими их по градиенту аналогами. Соответственно, в области близких точек бифуркаций будет существовать переходная зона. Если между видами существует некоторая конкуренция, то граница может быть резкой. Исследование этого типа границ требует многомерного анализа отношений видов к некоторым виртуальным факторам и отображения их изменения по градиенту среды (Пузаченко, 2004). Если получаемая на этой основе статистическая модель взаиморазмещения видов на трансекте генерирует наблюдаемые переходные зоны, то бифуркационный механизм можно считать доказанным. Бифуркационный механизм описывает многие процессы в природе: резкое изменение влажности почвы при изменении крутизны склона, геохимические барьеры и т.п.

Модель гистерезиса. Гистерезис описывает движение некоторой переменной по разным траекториям при увеличении и уменьшении значения определяющего ее фактора (Scheffer et al., 2001; Visintin, 2006; Beisner et al., 2008). Допустим, на некоторой территории в момент t₀ существует степь. Пусть происходит постепенное увеличение осадков и на месте степи формируется лес. Допустим, что наступил новый климатический цикл и постепенно количество осадков уменьшается. Однако лес не будет преобразовываться по той же траектории. Он может перейти скачкообразно в степь, если количество осадков будет существенно меньше, чем было в момент t₀. Приведем реальный пример гистерезиса возникшего на наших глазах на территории Центрально-лесного заповедника (наблюдения 1994–2017 гг.). На протяжении всего периода наблюдения наблюдается общий тренд потепления зимы (Шуйская, 2021). На наших глазах в еловых лесах на морене увеличилось участие клена, липы, вяза, а в кустарниковом ярусе – лещины (Пукинская, 2020). Однако, еловый лес все-таки остается еловым. В 1996 г. в результате ветровала еловый лес был уничтожен на значительной территории (Пузаченко, 2007). Летняя температура воздуха на ветровалах на 2–3 градуса выше, чем над еловым лесом. В результате возобновление леса пошло через широколиственные породы и, в первую очередь, через липу, клен и вяз. Сомкнутость полога настолько высока, что ель в возобновлении встречается единично. Вместе с тем ельники, не пострадавшие от ветровала, так и остаются ельниками и граница между ними и широколиственными лесами практически всегда резкая. Гистерезис широко распространен в природе. Для доказательства этого механизма возникновения резкой границы требуется обычно прямой или косвенный анализ изменения климата на исследуемой территории.

Уравнение реакции–диффузии с потоком Тьюринга. В основе простейшего варианта модели лежит классическая модель динамики популяции:

где x – переменная, r – коэффициент размножения (активатор), b – коэффициент самоингибирования (ингибитор).

Дополним модель пространством, в котором происходит диффузия ингибитора и активатора. Пространственные структуры, в том числе с резкими границами, возникают в зависимости от соотношения коэффициент диффузии ингибитора и активатора. В общем случае, если коэффициент диффузии ингибитора существенно больше коэффициента диффузии активатора, то возникают пространственные структуры (Turing, 1952; Ризниченко, 2003). Эта модель, например, хорошо описывает формирование дискретных пятен и полос растительности в семиаридном климате (Tian, 2015). Она, вероятно, будет описывать пространственные структуры в подзолистых почвах с частотой около 1000–500 берг. Модель порождает иерархическую организацию с правильно повторяющими полосами пространственных частот. Выявить потенциальную реализуемость этой модели можно на основе спектрального и вейвлет анализа, в рамках которого будут установлены иерархические уровни с кратными частотами. Возможность реализации этой модели в растительном покрове в умеренном климате проблематична, однако исключать ее реализуемость нельзя. Возможно, она реализуется на лугах при различных соотношениях коэффициентов расселения и действия коэффициентов диффузии ингибиторов, как отображения конкуренции видов в пространстве. Реалистичность этой модели для древесного яруса весьма сомнительна.

Модель на основе обратных положительных связей. Положительная обратная связь приводит к тому, что части системы взаимно усиливают друг друга. Если такую систему не ограничивает среда и она линейна, то система абсолютно неустойчива и эта аутокаталитическая реакция приведет к взрыву (Арманд, 1988). Однако в системе “животные–растения–почва” отношения обычно нелинейны, а среда определяет допустимую область существования. Примеров таких систем очень много. Типичным примером является верховое болото, формирующееся на основе положительной обратной связи “торф–сфагновые мхи”. Такие же отношения существуют между лесом и степью, в первую очередь. за счет положительной обратной связи между лесом и осадками и положительными обратными связями между луговой (степной) растительностью и почвами. При определенных климатических условиях и определенных условиях рельефа (обычно, южные экспозиции), вторичные луга весьма устойчивы и в лесной зоне. По-видимому, существуют аналогичные образования и в естественном лесу. Проблема выявления и исследования таких целостных систем состоит в том, что они в полной мере могут проявляться лишь в старых, никогда не подвергавшихся рубкам и пожарам, лесах. Таких лесов очень мало, и они имеют в этом плане огромную ценность. Лесные системы, построенные на основе обратных положительных связей, заведомо неравновесны и обладают собственными механизмами, повышающими их устойчивость. Исследование их имеет очень большое значение, так как дает основания для построения моделей формирования целостности в растительных сообществах и биогеоценозах. Критерием выделения таких систем является резкость и почти полная замкнутость границ. Если мы получили на основе анализа мультиспектральной дистанционной информации такие образования, то они должны стать предметом специального исследования, направленного на выявления конкретных механизмов поддержания целостности, а в идеале, и их моделирования.

Фактически рассмотренные четыре модели исчерпывают возможные механизмы возникновения переходных зон и границ. Ограниченность этого перечня делает поиск механизмов, объясняющих формирования различных вариантов переходных зон, вполне реалистичным.

ПРИМЕРЫ АНАЛИЗА СТРУКТУРЫ ПЕРЕХОДНЫХ ЗОН НА РЕАЛЬНЫХ ОБЪЕКТАХ

Оценка структуры границы по плотности почвы. На рис. 3 показан трансект с шагом 20 м, пересекающий моренную гряду в Центрально-Лесном биосферном заповеднике (максимальное положение озера Валдайского оледенения, которое, по-видимому, с юга подпиралось ледником). Песчаные озерные отложения мощностью в среднем 50–60 см с запада покрывает всю поверхность. С востока на склоне моренной гряды распространены супесчаные озерные отложения. В центральной, наиболее низкой части трансекта (точка –3), на глубине 4 м вскрываются микулинские торфяные отложения, подстилаемые сапропелем и озерными глинами. На уступе от 14 до 24 точки на глубине 4 м также вскрываются торфянистые отложения микулинского возраста. От точки 7 до точки 25 распространен разновозрастный ельник чернично-сфагновый четвертого бонитета на торфянисто-глеевых почвах со средней мощностью торфа 50 см (максимум 70) с возрастом порядка четырех тысяч лет.

Рис. 3.

Трансект через моренную гряду в Центрально-Лесном заповеднике. 1. Максимальное положение зеркала озера Валдайского оледенения. 2. Мини-трансект на границе сфагнового ельника и ветровала 1996 г. на месте широколиственно-елового леса на палево-подзолистых почвах, 3. Мини-трансект на переходе от граничной зоны верхового болота к мелколиственно-еловому лесу на палево-подзолистых почвах.

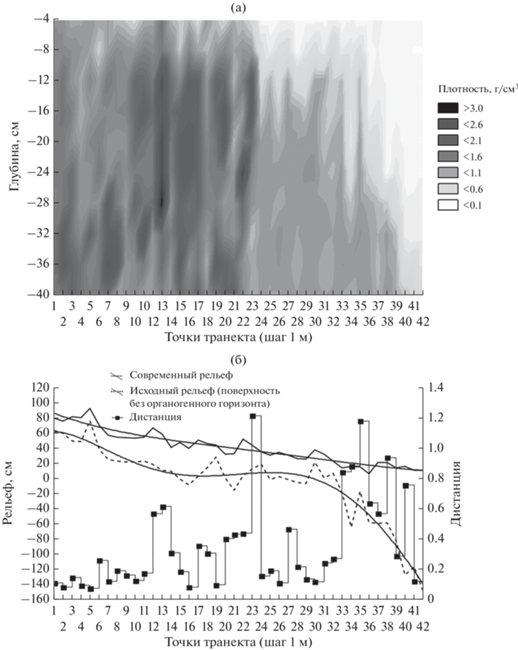
В торфе обнаруживаются захороненные стволы ели. Можно утверждать, что возраст этого уникального биогеоценоза исчисляется тысячелетиями. Эта суперустойчивость возникает в результате контура положительных обратных связей в системе “ель–сфагнум–торф”. Ель при относительно разреженном пологе (сомкнутость 0.5–0.6) обеспечивает необходимую освещенность для Sphagnum girgensohnii Russ. и Sphagnum angustifolium Russ. Формирование торфяного горизонта с низким минеральным питанием определяет развитие мощной корневой системы ели, делающую ее устойчивой к ветровалам, которые периодически уничтожают ельники на прилегающих моренных холмах. Покров сфагнума не препятствует успешному возобновлению ели в окнах, образующихся при выпадении единичных старых елей (возрастом около 250 лет). Прямые измерения баланса CO₂ показали, что в сухие годы биогеоценоз выделяет CO₂, а во влажные годы наоборот (Milyukova et al., 2002). В результате за 4000 лет накопилось только 50 см торфа. Рассматриваемый ельник является безусловным примером целостного биогеоценоза (экосистемы). От нулевой точки до шестой на трансекте распространено типично лесное сфагновое болото, резко отделенное от ельника. Ширина границы – один–два метра. Выпуклая форма поверхности определяется более интенсивным ростом сфагнума в центральной части болота. Переход от лесного болота к мелколиственно-еловому лесу постепенный. Доля сосны постепенно снижается. Болото, безусловно, наступает, так как на его границе около нулевой точки двадцать пять лет назад росли две ели, которые усохли примерно в 1993 г. (устное сообщение Е.С. Шапошникова). На рис. 4а представлено пространственное варьирование плотности почвы на мини-трансекте с шагом опробования 1 м на границе сфагнового ельника и ветровала (обозначен цифрой 2 на рис. 3), а на рис. 4б – современный и рельеф без органогенного горизонта (исходный рельеф). Плотность почвы определялась по образцам, отобранным буром (Робур, Volta, Россия) с шагом 4 см по глубине до 40 см. Почва формируется на озерных песках, перекрытых тонким слоем покровного суглинка. Морена, скорее всего, московского оледенения, вскрыта на глубине 1 м в точке № 41. На рис. 4б показана современная поверхность и поверхность без органогенного горизонта, для выделения резких границ рассчитывается квадратичная нормированная Евклидова дистанция для всего профиля до глубины 40 см с шагом 4 см:

Рис. 4.

Варьирование свойств почвы на мини-трансекте 1: а – Пространственное варьирование плотности почв, б – исходный рельеф, современный рельеф, дистанция между соседними точками по плотности почв.

где х – плотность почвы, i – номер точки, j – номер слоя почвы, которую с полным основанием можно назвать “мощностью границы”.

Из рис. 4б хорошо видно, как наступление ельника сфагнового в результате накопления торфа выравнивает исходный рельеф, однако оно происходит, по-видимому, пошагово. Выделяются четыре мощных резких интегральных границы по плотности на частоте 500 берг. Наибольшая мощность границы измерена в точке 23. На рис. 5 показано изменение плотности почвы для трех избранных характерных горизонтов: 4, 12, 32 см. Очевидно, что границы на рассматриваемой частоте для всех трех горизонтов резкие, но соответствуют разным точкам трансекта. Можно предположить, что в данном случае резкие границы могут быть объяснены моделью с положительной обратной связью между сфагнумом и образуемым им торфом, а наличие нескольких границ можно связать с циклическим изменением климата: торф активно накапливается во влажные периоды, а в сухие накопление прекращается. Это, в частности, подтверждается активным ростом сфагновых болот в последние влажные двадцать лет (Пузаченко и др., 2014). Выделенные резкие границы справедливы для частоты 500 берг. При большей частоте, например, 5000 берг (опробование через 10 см) они могут оказаться переходными. Очевидно, что это можно проверить, проведя отбор проб с соответствующей частотой. В идеале реалистичность модели будет доказана, если для верхнего горизонта резкая граница будет в среднем соответствовать радиальному продвижению сфагнума за один год.

Рис. 5.

Выделение резких границы по плотности почвы для трех характерных горизонтов.

На восточной части основного трансекта заложен второй мини-трансект с шагом опробования 1 м (обозначен цифрой 3 на рис. 3) для исследования границы в зоне перехода от торфянисто-глееватых почв с практически поверхностным положением грунтовых вод, к типичным палево-подзолистыми почвам с их более глубоким положением. Почвы сформированы на тонкозернистых озерных песках. На рис. 6 приведено пространственное варьирование относительной влажности по мини-трансекту на переходе от граничной зоны верхового болота к мелколиственно-еловому лесу. С первой по пятнадцатую точку мини-трансекта древесный ярус при сумме площадей сечений 20 м²/га образован на 85% елью и на 15% березой, далее до точки 30 древесный ярус образован елью, осиной, березой с сомкнутостью около 0.5. Травяной ярус разрежен и сформирован в основном осоками. Сфагновые мхи отсутствуют. Этот резкий переход хорошо виден на рис. 6: от первой до тринадцатой точки относительная влажность почвы у поверхности больше 90%, а затем быстро снижается до 70%. Далее, с 30 точки сумма площадей сечений возрастает до 23 м²/га, и в древостое уже господствует береза (ель – 26%, береза – 69% и осина 5%), далее до конца трансекта господствует осина (59%) с содоминатом – березой (26%) и 15% ели при сумме площадей сечений 27 м²/га. Травяной и моховой покров меняются по трансекту следующим образом: до шестой точки моховой покров состоит из сфагновых мхов с проективным покрытием до 90% и единичной черникой. В отличие от первого мини-трансекта, где сфагнум находился в оптимальных условиях и имел высоту зеленой части 10 см, на втором сфагнум угнетен с высотой зеленой части не более 3 см. Такое состояние сфагнума объясняется отрицательным влиянием достаточно мощного листового опада, исключающего его активную вегетацию поздней весной и в начале лета. С седьмой по тринадцатую точку проективное покрытие сфагнума снижается до 50% и с тринадцатой до шестнадцатой до 10–20%. Далее по мини-трансекту распространен более-менее однородный травяной покров с проективным покрытием до 20% состоящий из типичных бореальных видов: черники, звездчатки, папоротников.

Рис. 6.

Пространственное варьирование относительной влажности почвы на мини-трансекте 2.

На рис. 7а представлено пространственное варьирование плотности почвы на втором мини-трансекте, а на рис. 7б – рельеф и Евклидова дистанция по плотности почвы. Как следует из рис. 7б, современная поверхность практически ровная, а в исходном рельефе выражен небольшой подъем с запада на восток, в настоящее время полностью нивелированный накопленной торфянистой массой. То, что в рамках этого мини-трансекта формируется граничная зона, – очевидно, однако, она имеет очень сложную внутреннюю структуру: резкие границы разной мощности фиксируются во второй, шестой, восьмой, десятой, двадцатой и двадцать третей точках (рис. 7б). Граница была бы резкой и единственной, если ли бы измерения осуществлялись примерно через 20–25 м, т.е. на частоте 25–20 берг. Очевидно, что формирование торфянистого горизонта происходит по низинному типу заболачивания и маломощный сфагнум не оказывает существенного влияния, когда минерализация органического материала блокируется его высокой влажностью при очень большой влагоемкости. Сфагнум, по-видимому, заселяет поверхность, уже подготовленную этим процессом. Можно предположить, что в основе наступления низинного болота лежит, с одной стороны, механизм обратной положительной связи, а с другой, бифуркационные механизмы, переводящие систему скачкообразно из состояния хорошо “разлагаемая органика” в состояние “слабо разлагающаяся органика”. При этом движение управляющего параметра к точке бифуркации происходит за счет саморазвития на основе обратной положительной связи. В результате процесс в целом происходит скачкообразно с формированием серии резких границ. Конечно, в рассмотренных случаях механизмы объясняющие возникновение резких границ можно рассматривать не более как гипотетические.

Рис. 7.

Варьирование свойств почвы на мини-трансекте 2: а – пространственное варьирование плотности почв, б – исходный рельеф, современный рельеф, дистанция между соседними точками по плотности почв.

В идеале для каждого случая должна быть построена строгая математическая модель, воспроизводящая реальность. Однако и первый уровень качественного анализа возможных механизмов формирования резких границ представляется полезным. Приведенные два примера демонстрируют возможность исследования формирования резких границ в почве. В принципе, по аналогии такие исследования можно организовать и для почвы и растительности совместно. Однако, прежде чем перейти к исследованию деталей нужно идентифицировать положение резких границ и переходных зон для всей территории на основе мультиспектральной дистанционной информации.

Выделение границ на основе мультиспектральной дистанционной информации. На рис. 8 представлена территория, избранная для демонстрации отображения границ по мультиспектральной дистанционной информации.

Рис. 8.

Картосхема растительного покрова участка Центрально-лесного заповедника. Классификация по мультиспектральной съемке SPOT 6 (пространственное разрешение 6 × 6 м в пикселе) для частоты 83.3 берг.

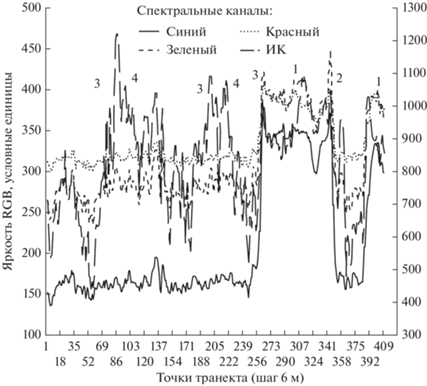
На рис. 9 изменение яркости в четырех спектральных каналах по трансекту в исходной пространственной частоте – пространственном разрешении съемки – 6 м. Трансект пересекает верховое болото, еловые леса и ветровалы.

Рис. 9.

Варьирование яркости в четырех каналах по трансекту: 1 – верховое болото, 2 – моренный холм с старым еловым лесом, 3 – еловый лес, 4 – ветровал 1964 г.

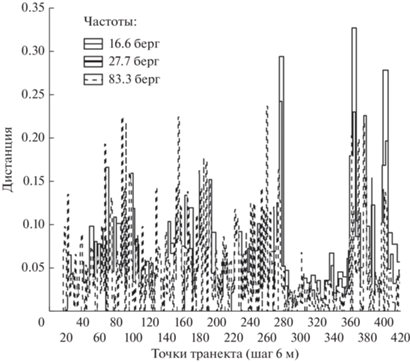
На рис. 10 приведена нормализованная дистанция Евклида, маркирующая резкие границы для трех частот: 83.3, 27.7 и 16.6 берг, рассчитанная по четырем каналам сьемки между соседними точками с заданной частотой, т.е.

Рис. 10.

Границы на трансекте – дистанции по яркостям для различных частот.

где b1x_i – первый спектральный канал i-той точки трансекта, b2x_i – второй и т.д.

Сравнение дистанций в этих трех частотах демонстрирует зависимость отображения резких границ от частоты. Так, резкая граница верхового болота выделяется на всех частотах. С другой стороны, резкая граница на самом болоте выделяется на частоте 83.3 берг, а вторая на частоте 16.6 берг и исчезает на более высоких частотах. Граница между еловым лесом и ветровалами хорошо выделяется на низких частотах и частично сохраняется на высокой частоте. На высокой частоте в пределах, как елового леса, так и ветровала появляются собственные резкие границы, исчезающие при низкочастотном отображении. Таким образом, используя мультиспектральные отображения и рассматривая их на различных частотах, получаем возможность исследовать внутреннюю структуру транзитных зон.

На рис. 11 приведены высокочастотные и низкочастотные границы для рассматриваемого участка территории (рис. 8). Граница определялась как максимум из трех направлений, по которым оценивалась метрика Евклида относительно центральной точки ядра свертки 3 × 3, идущей из левого верхнего угла изображения вправо построчно: с севера на юг, с северо-запада на юго-восток, с запада на восток. Можно записать выражение плавающего квадрата следующим образом

Рис. 11.

Границы на частоте 83.3 берг (а) и на частоте 16.6 берг (б).

где d(x_ij, x) – дистанция Евклида между центральной точкой ядра в исходном изображении и соседней точки в направлении заданном координатами ij.

Очевидно, что на низкой частоте разнообразие границ существенно меньше, чем на высокой. Фактически однозначно выделяются болота, переходная зона между болотом и камом и фрагмент на каме с двумя вариантами землепользования. Остальные границы весьма фрагментарны. На высокой частоте на верховых болотах появляются границы, выделяющие их разные варианты. На лесной территории выделяются часто замкнутые границы разной контрастности. Очевидно, что во всех случаях можно измерить полосу частот границ и, если необходимо исследовать их внутреннюю структуру, отображаемую в мультиспектральных измерениях. Возможности выделения границ по дистанционным измерениям создаются основу для их прямого исследования в поле.

Методы исследования границ и целостности в природе. Индивидуалистическая модель сообщества отображает равновесные отношения между видами, в то время как организменная – неравновесные. Обе модели одновременно реализуются в системе. Границы, выделяемые по мультиспектральным измерениям из космоса, априори демонстрируют области нарушения равновесия и их исследования позволяют подойти к пониманию порождающих их механизмов. По сути, в них сосредоточена информация об организации системы в целом. Естественно, по дистанционной информации выделяется множество границ и случайный выбор при их исследовании не продуктивен. Очевидно, достаточно рассмотреть их для следующих комбинаций внешних переменных: 1) старые леса и ветровалы, молодые и вообще вторичные леса, 2) ровные поверхности – склоны, 3) суглинки – пески. Таким образом, получаем восемь основных комбинаций, что с учетом четырех-пяти кратной повторности, составляет тридцать-сорок точек. Это, конечно, минимум, с которого можно начинать исследования. Практика показала, что границы, выделенные по дистанционной информации SPOT 6, практически всегда хорошо идентифицируются на местности, в интервале 6–12 м. Для экспресс-анализа границы закладываем ортогональный к границе трансект длиной 30–40 м с нивелировкой через 1 м. Используя панорамную цифровую камеру высокого разрешения, фотографируем растительность по обе стороны границы. Качество цифровой фотографии позволяет точно различать виды деревьев и подсчитать их число. В десяти метрах от границы слева и справа закладываем стандартные геоботанические площадки и фотографируем кроны фотоаппаратом с объективом Fish-Eye для оценки индекса листовой поверхности. На каждой точке трансекта фотографируем травяной покров на площадке 1 × 1 м и измеряем влажность почвы на глубинах 20 и 10 см с помощью влагомера TDR-300 (Field Scout, США). Качество фотографии обычно позволяет определить виды и их проективное покрытие. С шагом в пять метров бурим почву до глубины два метра, для того чтобы определить однородны ли условия почвообразования и не является ли граница следствием смены механического состава почвы. В случае подозрения на то, что граница определяется сменой механического состава, сгущаем бурение в области границы. В результате, в первом приближении, можно установить, определяется ли граница внешними факторами: перегибом рельефа, его постепенным изменением или сменой почвообразующих пород, оцениваем, является ли она сменой функционирования растительности, которая возможно определяют бифуркацию. Если внешние переменные неизменны, то граница, скорее всего, определяется положительными обратными связями между особями одного вида обычно с корневым возобновлением (например, осина), положительными связями в травяном ярусе между видами, включая возобновление деревьев и кустарников. Таким образом, уже на первом этапе можно систематизировать типы границ по их возможному генезису на основе экспресс-описания, а затем уже перейти к детальному исследованию порождающих их механизмов в избранных точках. Естественно, по мере развития исследования потребуются дополнительный анализ особо характерных, замкнутых границ.

ЗАКЛЮЧЕНИЕ

Для развития рассматриваемых здесь представлений требуется разработка соответствующих теоретико-методологических оснований, адекватных методов полевых исследований, использования дистанционной информации и новых методов анализа данных. Не менее важна смена парадигмы, которая в данном случае сводится к представлению о ландшафте как нелинейной, неравновесной динамической системы и представлении о том, что в области нарушения равновесия сосредоточена основная информация о механизмах определяющих динамику и эволюцию системы. Это предполагает развитие базовых знаний теории динамических систем и новых технологий. Вместе с тем формулировка проблемы и ее общие теоретико-методологические основания представляются нам необходимыми уже сейчас. Можно надеяться, что некоторые, продемонстрированные в настоящей работе технические приемы могут быть использованы в исследованиях и в настоящее время.