1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 83, № 11, 2019

Известия РАН. Серия физическая, 2019, T. 83, № 11, стр. 1514-1518

Биполярные потоки с зарядовой и токовой компенсацией

М. А. Завьялов 1, Т. М. Сапронова 1, *, В. А. Сыровой 1

1 Всероссийский электротехнический институт – филиал федерального государственного унитарного предприятия “Российский федеральный ядерный центр – Всероссийский научно-исследовательский институт технической физики имени академика Е.И. Забабахина”
Москва, Россия

* E-mail: sapron0109@mail.ru

Поступила в редакцию 20.05.2019
После доработки 20.06.2019
Принята к публикации 27.07.2019

Полный текст (PDF)

Аннотация

Рассмотрены одномерные потоки заряженных частиц с противоположными знаками зарядов, движущихся в одном направлении: электронный диод (или диод с отрицательными ионами), простреливаемый положительными ионами; ионный диод, пронизываемый релятивистскими электронами. Исследованы варианты с различной степенью компенсации пространственного заряда на выходе из диода, а также случай полной компенсации по заряду, току и магнитному полю.

ВВЕДЕНИЕ

Интерес к биполярным электронно-ионным потокам со встречным движением компонент после классической работы И. Лэнгмюра [1] привел к рассмотрению одномерных нерелятивистских течений в цилиндрическом и сферическом диодах [2] с экспериментальной апробацией результатов [3], исследованию режимов плоского диода в униполярном и биполярном вариантах с дополнительной инжекцией ионов с плоскости между анодом и катодом [4], изучению влияния ненулевой начальной скорости при произвольных условиях инжекции на электродах и встречном движении компонент [5]. Последние работы посвящены исследованию эффекта релятивистских скоростей электронов [6], режима “ионного фонтана” [7] и расходящегося электронного потока в цилиндрическом и сферическом биполярных диодах [8].

В режиме “ионного фонтана” для ионов имеет место двухпоточный режим: между катодом и плоскостью отражения ионы, тормозясь, движутся в положительном направлении и равный им по интенсивности ионный поток, ускоряясь, возвращается к катоду. При начальной энергии ионов, превышающей энергию электронов на аноде, отражение не реализуется и, начиная с плоскости анода, можно говорить об условиях компенсации электронно-ионного пучка. Несколько расширив обычное понятие биполярного потока как встречного движения электронов и ионов, будем определять этим термином течение, образованное двумя видами частиц с противоположным знаком заряда (например, отрицательными и положительными ионами) вне зависимости от направления их движения. Работа посвящена рассмотрению одномерных режимов, когда диод с одним видом частиц простреливается плотным потоком зарядов противоположного знака при возможных комбинациях ролей компонент: электронный диод, пронизываемый ионами; ионный диод, пронизываемый электронами; диод, в котором электроны заменены отрицательными ионами.

Рассмотрение ведется в безразмерных переменных

(1)
$\begin{gathered} \bar {r} = \frac{r}{{L{\text{*}}}},\,\,\,\,{\bar {v}} = \frac{{v}}{{V{\text{*}}}},\,\,\,\,\bar {\varphi } = \frac{\varphi }{{\left( {{{V_{*}^{2}} \mathord{\left/ {\vphantom {{V_{*}^{2}} {{{\eta }_{e}}}}} \right. \kern-0em} {{{\eta }_{e}}}}} \right)}}, \\ \bar {\rho } = \frac{\rho }{{\left( {{{{{\varepsilon }_{0}}V_{*}^{2}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}V_{*}^{2}} {{{\eta }_{e}}L_{*}^{2}}}} \right. \kern-0em} {{{\eta }_{e}}L_{*}^{2}}}} \right)}},\,\,\,\,\bar {J} = \frac{J}{{\left( {{{{{\varepsilon }_{0}}V_{*}^{3}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}V_{*}^{3}} {{{\eta }_{e}}L_{*}^{2}}}} \right. \kern-0em} {{{\eta }_{e}}L_{*}^{2}}}} \right)}}, \\ \end{gathered} $
где проведенные нормировки (черточка сверху) соответствуют расстоянию, скорости, потенциалу, плотности пространственного заряда и плотности тока; ${{\eta }_{e}} = {e \mathord{\left/ {\vphantom {e m}} \right. \kern-0em} m},$ ${{\varepsilon }_{0}}$ – удельный заряд электрона и диэлектрическая проницаемость вакуума; $L{\text{*,}}$ $V{\text{*}}$ – характерные значения длины и скорости. В качестве $L{\text{*}}$ удобно выбрать расстояние катод-анод, а $V{\text{*}}$ в нерелятивистском случае связать с потенциалом анода ${{\varphi }_{A}}.$ $V_{*}^{2} = {{\eta }_{e}}{{\varphi }_{A}},$ при релятивистских энергиях $V{\text{*}} = c.$

ИНЖЕКЦИЯ ИОНОВ ИЗ-ЗА КАТОДА

Уравнения пучка

Эмиссия электронов с плоскости $z = 0$ происходит в режиме ограничения пространственным зарядом (ρ-режим), ионы инжектируются из-за катода с энергией, соответствующей потенциалу ${{\varphi }_{i}} = {{\varphi }_{A}} + {{\varphi }_{\Delta }}.$ Уравнения пучка сводятся к соотношению для потенциала φ:

(2)
$\frac{{{{d}^{2}}\varphi }}{{d{{z}^{2}}}} = \frac{{{{J}_{e}}}}{{\sqrt {2\varphi } }} - \frac{{{{J}_{i}}}}{{\sqrt {2\mu \left( {1 + {{\varphi }_{\Delta }} - \varphi } \right)} }},\,\,\,\,\mu = \frac{{{{\eta }_{i}}}}{{{{\eta }_{e}}}}.$

Двукратное интегрирование с выполнением условий ρ-режима при $z = 0$ ($\varphi = \varphi {\kern 1pt} ' = 0$) приводит к следующему результату

(3)
$\begin{gathered} \frac{1}{2}{{\left( {\frac{{d\varphi }}{{dz}}} \right)}^{2}} = \\ = {{J}_{e}}\left\{ {\sqrt {2\varphi } + \alpha \left[ {\sqrt {2\left( {1 + {{\varphi }_{\Delta }} - \varphi } \right)} - \sqrt {2\left( {1 + {{\varphi }_{\Delta }}} \right)} } \right]} \right\}, \\ \sqrt {2{{J}_{e}}} z = \\ = \int\limits_0^\varphi {\frac{{dt}}{{\sqrt {\sqrt {2t} + \alpha \left[ {\sqrt {2\left( {1 + {{\varphi }_{\Delta }} - t} \right)} - \sqrt {2\left( {1 + {{\varphi }_{\Delta }}} \right)} } \right]} }}} \equiv \\ \equiv I\left( {\varphi ;{{\varphi }_{\Delta }}} \right),\,\,\,\,\alpha = \frac{1}{{\sqrt \mu }}\frac{{{{J}_{i}}}}{{{{J}_{e}}}}. \\ \end{gathered} $

Электронный диод, полная компенсация

Условие компенсации по пространственному заряду ${{\rho }_{e}} = {{\rho }_{i}}$ при $z = 1,$ $\varphi = 1$ имеет вид

(4)
$\frac{{{{J}_{e}}}}{{\sqrt 2 }} = \frac{{{{J}_{i}}}}{{\sqrt {2\mu {{\varphi }_{\Delta }}} }},\,\,\,\,\alpha = \sqrt {{{\varphi }_{\Delta }}} .$

Дополнительное требование равенства скоростей ${{v}_{e}} = {{v}_{i}},$ а, следовательно, и плотностей токов ${{J}_{e}} = {{J}_{i}},$ определяет значение ${{\varphi }_{\Delta }}$: ${{\varphi }_{\Delta }} = \frac{1}{\mu }.$

Это условие может быть реализовано только для низкоэнергетических электронов (энергия порядка 100 эВ при энергии ионов водорода 180 кэВ).

Из формул (4) следует величина электронного тока

(5)
${{J}_{e}} = \frac{1}{2}{{I}^{2}}\left( {1;\,{{\varphi }_{\Delta }}} \right).$

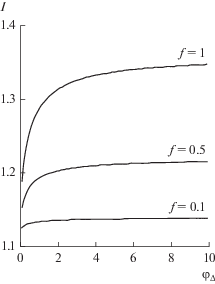
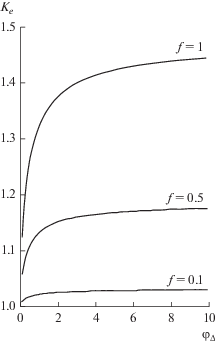
Главной целью в рассматриваемой задаче являются условия компенсации по заряду и току. На рис. 1, 2 и 3 представлены зависимости $I\left( {1;\,{{\varphi }_{\Delta }}} \right),$ ${{K}_{e}}\left( {{{\varphi }_{\Delta }}} \right)$ и ${{{{J}_{i}}\left( {{{\varphi }_{\Delta }}} \right)} \mathord{\left/ {\vphantom {{{{J}_{i}}\left( {{{\varphi }_{\Delta }}} \right)} \mu }} \right. \kern-0em} \mu }.$

Рис. 1.

Зависимость I(1; φΔ).

Рис. 2.

Зависимость Ke(φΔ).

Рис. 3.

Зависимость Ji(φΔ)/μ.

Диод с отрицательными ионами и инжекцией положительных ионов из-за катода

В случае, когда электроны заменены отрицательными ионами, имеют место приведенные выше формулы с измененным смыслом параметров:

(6)
${{J}_{e}} \to {{J}_{ - }},\,\,\,\,{{J}_{i}} \to {{J}_{ + }},\,\,\,\,\alpha \to \frac{1}{{\sqrt \mu }}\frac{{{{J}_{ + }}}}{{{{J}_{ - }}}},\,\,\,\,\mu \to \frac{{{{\eta }_{ + }}}}{{{{\eta }_{ - }}}}.$

Электронный диод, частичная компенсация

При выполнении требования ${{\rho }_{i}} = f{{\rho }_{e}}$ выражение для $\alpha $ принимает вид

(7)
$\alpha = \sqrt {{{\varphi }_{\Delta }}} f.$

Асимптотика интеграла I из (3) при ${{\varphi }_{\Delta }} \to \infty $ описывается формулой

(8)
$I = 2\sqrt[4]{2}\left\{ {\frac{1}{{{{f}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}\left[ {\frac{\pi }{2} - \arcsin \left( {1 - f} \right)} \right] - \frac{{\sqrt {2 - f} }}{f}} \right\}.$

На рис. 1–3 приведены кривые для $f = 0.5,$ 0.1, аналогичные случаю полной компенсации в плоскости анода. Формула (8) имеет смысл при $f \leqslant 2,$ причем при $f > 1$ следует говорить о режиме перекомпенсации. Коэффициент компенсации ${{f}_{\infty }} = 2$ при конечной величине ${{\varphi }_{\Delta }}$ соответствует критическим значениям параметров $\alpha = \alpha *,$ $f = f*,$ для которых электрическое поле на аноде обращается в нуль:

(9)
$\begin{gathered} \alpha * = \frac{1}{{\sqrt {1 + {{\varphi }_{\Delta }}} - \sqrt {{{\varphi }_{\Delta }}} }} = \sqrt {1 + {{\varphi }_{\Delta }}} + \sqrt {{{\varphi }_{\Delta }}} ; \\ f* = 1 + \sqrt {1 + \frac{1}{{{{\varphi }_{\Delta }}}}} . \\ \end{gathered} $

Видно, что в режиме полной компенсации $f = 1$ равенства (9) не могут быть реализованы, так как $f{\text{*}}$ всегда больше единицы. Интеграл I и коэффициент усиления ${{K}_{e}}$ при ${{\varphi }_{\Delta }} \to \infty ,$ ${{f}_{\infty }} = 2$ принимают следующие значения $I = \frac{\pi }{{\sqrt[4]{2}}},$ ${{K}_{e}}$ = = $\frac{9}{{16}}{{\pi }^{2}} \approx 5.552.$ При $\alpha > \alpha {\text{*}}$ квадрат поля на аноде становится отрицательным, а поскольку рост этого параметра обусловлен увеличением инжектируемого ионного тока, то интересно выяснить, что происходит при дальнейшем усилении перекомпенсации. Ответ состоит в том, что при $\alpha > \alpha {\text{*}}$ изменяется режим эмиссии электронов: поле на катоде становится положительным, а электронный ток в Т-режиме достигает максимального значения, определяемого свойствами эмитирующей поверхности. Выражение для электрического поля из (3) принимает вид

(10)
$\begin{gathered} \frac{1}{2}{{\left( {\frac{{d\varphi }}{{dz}}} \right)}^{2}} = \\ = \sqrt 2 {{J}_{e}}\left[ {\sqrt \varphi - 1 + \alpha \left( {\sqrt {1 + {{\varphi }_{\Delta }} - \varphi } - \sqrt {{{\varphi }_{\Delta }}} } \right)} \right] + \frac{1}{2}E_{A}^{2}, \\ \end{gathered} $
где ${{E}_{A}}$ – поле на аноде. Записывая это соотношение на катоде, получаем

(11)
$\frac{1}{2}\left( {E_{C}^{2} - E_{A}^{2}} \right) = \sqrt 2 {{J}_{e}}\left[ {\alpha \left( {\sqrt {1 + {{\varphi }_{\Delta }}} - \sqrt {{{\varphi }_{\Delta }}} } \right) - 1} \right].$

При $\alpha > \alpha {\text{*}}$ выражение в правой части больше нуля. В рассматриваемом случае для фиксированного значения ${{J}_{e}}$ мы можем распоряжаться только ионным током и энергией ионов. При этом оказывается, что заданному набору физических величин соответствует множество режимов с разными значениями ${{E}_{C}} > {{E}_{A}},$ связанными соотношением (11). Аналог интеграла I из (8) для электрического поля, удовлетворяющего соотношению (10), при ${{\varphi }_{\Delta }} \to \infty $ определяется выражением

(12)
$\begin{gathered} I = \frac{{2\sqrt 2 }}{f}\left( {\frac{1}{{\sqrt {E_{A}^{2} + {f \mathord{\left/ {\vphantom {f 2}} \right. \kern-0em} 2} - 1} }} - {{E}_{A}}} \right) + \\ + \,\,\frac{{\sqrt 2 }}{{{{f}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}\left[ {\arcsin \frac{{1 - f}}{{\sqrt {2fE_{A}^{2} + {{{\left( {f - 1} \right)}}^{2}}} }} - } \right. \\ \left. { - \,\,\arcsin \frac{1}{{\sqrt {2fE_{A}^{2} + {{{\left( {f - 1} \right)}}^{2}}} }}} \right]. \\ \end{gathered} $

Формула (12) имеет смысл при произвольной степени перекомпенсации, если выполнены условия (11).

ИНЖЕКЦИЯ ЭЛЕКТРОНОВ ИЗ-ЗА АНОДА

Диод с положительными ионами, полная компенсация

Случай, когда частицы меняются местами, причем электроны остаются нерелятивистскими, не требует независимого рассмотрения. При этом для ионов на аноде выполнены условия ${\rho }$-режима, а электроны инжектируются из-за анода в сторону катода $v_{i}^{2} = 2\mu \left( {1 - \varphi } \right),$ $v_{e}^{2} = 2\left( {\varphi + {{\varphi }_{{\Delta e}}}} \right).$ Отметим звездочкой электронный ток, определяемый формулой (6). При той же избыточной энергии электронов ${{\varphi }_{\Delta }} = {{\varphi }_{{\Delta e}}}$ ионный ток в ρ-режиме равен ${{J}_{i}} = \sqrt \mu J_{e}^{*}.$ Электронный ток определяется интегралом

(13)
$\begin{gathered} \sqrt {2{{J}_{e}}} = \\ = \int\limits_0^1 {\frac{{dt}}{{\sqrt {\left[ {\sqrt {2\left( {t + {{\varphi }_{{\Delta e}}}} \right)} - \sqrt {2\left( {1 + {{{\varphi }}_{{\Delta e}}}} \right)} + {{\sqrt {2\left( {1 - t} \right)} } \mathord{\left/ {\vphantom {{\sqrt {2\left( {1 - t} \right)} } {\sqrt {{{{\varphi }}_{{\Delta e}}}} }}} \right. \kern-0em} {\sqrt {{{{\varphi }}_{{\Delta e}}}} }}} \right]} }}} = \\ = \sqrt[4]{{{{{\varphi }}_{{\Delta e}}}}}I\left( {1;\,{{{\varphi }}_{{\Delta e}}}} \right),\,\,\,\,{{J}_{e}} = \frac{1}{2}{{I}^{2}}\left( {1;\,{{{\varphi }}_{{\Delta e}}}} \right)\sqrt {{{{\varphi }}_{{\Delta e}}}} . \\ \end{gathered} $

Условие компенсации по пространственному заряду приводит к следующему значению параметра $\alpha = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{{\varphi }}_{{\Delta e}}}} }}} \right. \kern-0em} {\sqrt {{{{\varphi }}_{{\Delta e}}}} }}.$ При дополнительном требовании равенства скоростей имеем ${{{\varphi }}_{{\Delta e}}} = \mu .$

Учет релятивистских эффектов для инжектируемых электронов

При энергии ионов, соответствующей потенциалу в несколько сотен киловольт, электроны становятся релятивистскими при этом

(14)
$\begin{gathered} v_{i}^{2} = 2\mu \left( {{{{\varphi }}_{A}} - \varphi } \right), \\ v_{e}^{2} = \frac{{\left( {\varphi + {{\varphi }_{{\Delta e}}}} \right)\left( {2 + \tilde {\varphi } + {{{{\tilde {\varphi }}}}_{{\Delta e}}}} \right)}}{{{{{\left( {1 + \tilde {\varphi } + {{{{\tilde {\varphi }}}}_{{\Delta e}}}} \right)}}^{2}}}}. \\ \end{gathered} $

Тильдой отмечены исчезающие в нерелятивистском пределе члены. Распределения поля и потенциала в этом случае отличаются от ранее рассмотренного варианта

(15)
$\begin{gathered} \frac{1}{2}{{\left( {\frac{{d\varphi }}{{dz}}} \right)}^{2}} = {{J}_{e}}\left[ {\sqrt {\left( {\varphi + {{\varphi }_{{\Delta e}}}} \right)\left( {2 + \tilde {\varphi } + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right) - } } \right. \\ \left. { - \,\,\sqrt {\left( {{{\varphi }_{A}} + {{\varphi }_{{\Delta e}}}} \right)\left( {2 + \tilde {\varphi } + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} + \alpha \sqrt {2\left( {{{\varphi }_{A}} - \varphi } \right)} } \right], \\ \sqrt {2{{J}_{e}}} z = \int\limits_0^{\varphi } {\left[ {\sqrt {\left( {t + {{\varphi }_{{\Delta e}}}} \right)\left( {2 + \tilde {t} + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} } \right.} - \\ - \,\,\sqrt {\left( {{{\varphi }_{A}} + {{\varphi }_{{\Delta e}}}} \right)\left( {2 + {{{\tilde {\varphi }}}_{A}} + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} + \\ + \,\,{{\left. {\alpha \sqrt {2\left( {{{\varphi }_{A}} - t} \right)} } \right]}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}dt. \\ \end{gathered} $

Условие компенсации по пространственному заряду в плоскости катода определяется формулой

(16)
$\alpha = \frac{{\sqrt {2{{\varphi }_{A}}} \left( {1 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)}}{{\sqrt {{{\varphi }_{{\Delta e}}}\left( {2 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} }}.$

Требование равенства скоростей обеих компонент потока имеет вид

(17)
${{\varphi }_{{\Delta e}}} = \frac{1}{{\sqrt {1 - 2\mu {{\varphi }_{A}}} }} - 1.$

Частичная компенсация с релятивистскими электронами

При частичной компенсации заряда в ионном диоде ${{\rho }_{e}} = {{f}_{e}}{{\rho }_{i}}$ выражение для α принимает вид

(18)
$\alpha = \frac{1}{{\sqrt \mu }}\frac{{{{J}_{i}}}}{{{{J}_{e}}}} = \frac{1}{{{{f}_{e}}}}\frac{{\sqrt {2{{\varphi }_{A}}} \left( {1 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)}}{{\sqrt {{{\varphi }_{{\Delta e}}}\left( {2 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} }}.$

Нарушение эмиссии ионов в ρ-режиме с анода при перекомпенсации должно иметь место и в этом случае при выполнении условия

(19)
$\begin{gathered} E_{С}^{2} = 2{{J}_{e}}\left[ {\sqrt {{{\varphi }_{{\Delta e}}}\left( {2 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} } \right. - \\ \left. { - \,\,\sqrt {\left( {{{\varphi }_{A}} + {{\varphi }_{{\Delta e}}}} \right)\left( {2 + {{{\tilde {\varphi }}}_{A}} + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} + \alpha \sqrt {2{{\varphi }_{A}}} } \right] < 0. \\ \end{gathered} $

Подстановка α из (18) в (19) приводит к квадратному трехчлену для ${{f}_{e}}{\text{:}}$

(20)
$\begin{gathered} F \equiv f_{e}^{2} - 4\frac{{1 + {{{\tilde {\varphi }}}_{{\Delta e}}}}}{{{{{\tilde {\varphi }}}_{A}} + 2\left( {1 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)}}{{f}_{e}} - \\ - \,\,4{{\varphi }_{A}}\frac{{{{{\left( {1 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)}}^{2}}}}{{{{\varphi }_{{\Delta e}}}\left( {2 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)\left[ {{{{\tilde {\varphi }}}_{A}} + 2\left( {1 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} \right]}} > 0. \\ \end{gathered} $

Уравнение $F = 0$ имеет действительные корни разного знака, причем $F\left( 0 \right) < 0.$ Таким образом, неравенство (20) выполняется при значении ${{f}_{e}}$, превышающем критическую величину $f{\text{*:}}$

(21)
$\begin{gathered} {{f}_{e}} > f{\text{*}} = 2\frac{{1 + {{{\tilde {\varphi }}}_{{\Delta e}}}}}{{{{{\tilde {\varphi }}}_{A}} + 2\left( {1 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)}} \times \\ \times \,\,\left\{ {1 + \sqrt {1 + \frac{{{{\varphi }_{A}}\left[ {{{{\tilde {\varphi }}}_{A}} + 2\left( {1 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} \right]}}{{{{\varphi }_{{\Delta e}}}\left( {2 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)}}} } \right\}. \\ \end{gathered} $

В нерелятивистском случае значение $f{\text{*}}$ совпадает с формулой (9). Соотношение для поля на катоде и аноде, аналогичное (11), имеет вид

(22)
$\begin{gathered} \frac{1}{2}\left( {E_{A}^{2} - E_{C}^{2}} \right) = \\ = {{J}_{e}}\left[ {\sqrt {\left( {{{\varphi }_{A}} + {{\varphi }_{{\Delta e}}}} \right)\left( {2 + {{{\tilde {\varphi }}}_{A}} + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} - } \right. \\ \left. { - \,\,\sqrt {{{\varphi }_{{\Delta e}}}\left( {2 + {{{\tilde {\varphi }}}_{{\Delta e}}}} \right)} - \alpha \sqrt {2{{\varphi }_{A}}} } \right] > 0. \\ \end{gathered} $

Предельное значение критического коэффициента компенсации для релятивистских электронов при ${{\varphi }_{{\Delta {\kern 1pt} e}}} \to \infty $ оказывается тем же, что и для нерелятивистских ионов в электронном диоде: ${{f}_{\infty }} = 2.$

В работе [14] приведена схема режима “ионного фонтана” с использованием ионного потока для нагрева термоэмиссионного катода пушки с “тыльной” стороны за счет ионной бомбардировки. Дана оценка основных параметров модели плоского диода с инжекцией ионов для нагрева катода с использованием данных работ [3, 15].

ЗАКЛЮЧЕНИЕ

Предложенная модель одномерного движения биполярного потока с проницаемыми электродами может быть реализована при балансе между прозрачностью катода и площадью эмиссионной поверхности, который возможно реализовать при современных технологиях. Многопучковая ионная микроструктура в электронном диоде близка к одномерной биполярной модели при поперечном размере пучка, значительно превышающем микромасштаб, и соответствующей системе формирующих электродов [9].

Электронно-ионные пучки с компенсацией по пространственному заряду и току при движении компонент в одном направлении являются интересным электрофизическим объектом для ряда прикладных задач в области материаловедения, электротехники, микро- и наноэлектроники: модификация поверхностей материалов (включая диэлектрики) с одновременным воздействием электронных и ионных потоков; нагрев, травление, распыление, осаждение, размерная обработка, литография, ионная имплантация.

Пучки с компенсацией могут по заряду и току транспортироваться в вакууме на большие расстояния, представляя по этой причине альтернативный вариант по отношению к традиционным способам передачи электроэнергии [10]. При инжекции в космическое пространство для создания тяги они не возмущают потенциал космического аппарата.

Рассмотренные выше вопросы актуальны для физики, техники и технологии применения интенсивных ионных пучков [11]. Эффект расширения таких пучков при транспортировке в высоком вакууме проявляется в гораздо большей степени, чем в случае электронных потоков. Сравнение можно провести, пользуясь универсальной зависимостью, описывающей разлет произвольного релятивистского пучка заряженных частиц в дрейфовом пространстве [12].

В [11] для пучка протонов с током 1 А, энергией 10 кэВ и начальным радиусом 1 см приведены следующие оценки: на расстоянии 1 см пучок расширяется в два раза, на длине в 50 см он увеличивает радиус в 100 раз. Для борьбы с этим эффектом, как в электронных, так и в ионных пучках является введение в поток зарядов противоположного знака. В монографии [11] приведены примеры различных способов компенсации пространственного заряда ионных пучков. Один из них – образование “синтезированного” потока при прохождении электронного пучка через ионный источник – близок к рассмотренной в этой работе схеме.

Исследованная модель одномерного частично компенсированного однонаправленного движения ионно-электронного потока напоминает ситуацию с “электронным охлаждением”, идея которого была предложена Г.И. Будкером.

Список литературы

  1. Langmuir I. // Phys. Rev. 1929. V. 33. № 6. P. 954.

  2. Белкин В.М., Завьялов М.А., Камунин А.А. // Радиотехн. и электроника. 1976. Т. 21. № 12. С. 2646.

  3. Завьялов М.А., Крейндель Ю.Е., Новиков А.А. и др. Плазменные процессы в технологических электронных пушках. М.: Энергоатомиздат, 1989.

  4. Акимов П.И., Богословская А.Б. // Прикл. физ. 2002. № 4. С. 90.

  5. Howes W.L. // J. Appl. Phys. 1965. V 36. № 6. P. 2039.

  6. Белкин В.М., Завьялов М.А., Сыровой В.А. // Радиотехн. и электроника. 2011. Т. 56. № 2. С. 212.

  7. Завьялов М.А., Стальков П.М., Сыровой В.А. // Радиотехн. и электроника. 2017. Т. 62. № 8. С. 799.

  8. Завьялов М.А., Сыровой В.А. // Радиотехн. и электроника. 2016. Т. 61. № 4. С. 380.

  9. Неганова Л.А., Плохов В.В., Сыровой В.А. // Радиотехн. и электроника. 1997. Т. 42. № 4. С. 479.

  10. Абрамян Е.А., Альтеркоп Б.А., Кулешов Г.Д. Интенсивные электронные пучки. М.: Энергоатомиздат, 1984.

  11. Коваль Н.Н., Окс Е.М., Протасов Ю.С. и др. Эмиссионная электроника. М.: МГТУ им. Н.Э. Баумана, 2009.

  12. Сыровой В.А. Введение в теорию интенсивных пучков заряженных частиц. М.: Энергоатомиздат, 2004.

  13. Молоковский С.И., Сушков А.Д. Интенсивные электронные и ионные пучки. М.: Энергия, 1972.

  14. Завьялов М.А., Сыровой В.А. // Тр. VI межд. Крейнделевского семин. “Плазменная эмиссионная электроника”. (Улан-Удэ, 2018). С. 21.

  15. Габович М.Д. Физика и техника плазменных источников ионов. М.: Атомиздат, 1972.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал