Известия РАН. Серия физическая, 2019, T. 83, № 2, стр. 233-238

ВВЕДЕНИЕ

Новосибирский лазер на свободных электронах (НЛСЭ) [1, 2] является источником монохроматического, перестраиваемого по частоте терагерцевого излучения, имеющим самую высокую среднюю мощность в мире. Пучок лазера после прохождения через транспортный канал на входе в рабочие станции с хорошей точностью является гауссовым. Для некоторых экспериментов, однако, требуется либо трансформация модового состава пучка, либо фокусировка излучения с заданным распределением интенсивности на заданные площади или в заданные объемы. В экспериментальных работах на НЛСЭ [3–9] было показано, что для трансформации мощного терагерцевого излучения удобнее всего использовать дифракционные оптические элементы, которые в рамках физической оптики можно рассматривать как амплитудно-фазовые транспаранты (АФТ). В ряде экспериментов, таких как терагерцевая голография [10] и дифракция пучков сложного модового состава на решетках [11], объекты также представляют собой АФТ.

Для планирования и сопровождения экспериментов на НЛСЭ был создан пакет программ WaveThruMasks в среде Matlab для расчетов прохождения пучка через последовательность амплитудно-фазовых транспарантов. Хотя имеется ряд коммерческих программ, позволяющих выполнять подобные расчеты (например, ZEMAX), созданный пакет имеет ряд преимуществ для обработки данных, полученных на НЛСЭ. Он достаточно “легкий”, его интерфейс удобен для пользователя, в программе заложен ряд наиболее часто используемых транспарантов. Пакет позволяет считывать и обрабатывать данные матричных микроболометрических приемников [12, 13], разработанных в Институте физики полупроводников СО РАН, записанных в нестандартных форматах *.tab и *.tvid. Ценность программы состоит также в том, что при экспериментах на НЛСЭ пучковое время для каждого пользователя ограничено, поэтому после проверки факта совпадения результатов расчетов с экспериментом, исследователь имеет возможность выполнить численно параметрические исследования явления и спланировать дальнейшие эксперименты.

Далее мы опишем алгоритм программы и численную схему расчетов, а также приведем пример использования программы для расчетов формирования бесселевых пучков с орбитальным угловым моментом с помощью бинарного фазового аксикона и дифракции этого пучка на двумерных периодических решетках.

АЛГОРИТМ РАСЧЕТОВ

Дифракция электромагнитной волны на некотором объекте в скалярной теории дифракции может быть описана математически с помощью интегралов Френеля–Кирхгофа или Релея–Зоммерфельда. Первый является более общим решением, а второй, выражение которого несколько проще, справедлив для случая плоских транспарантов. Наша задача относится к последнему случаю (рис. 1), поэтому используем интеграл Релея–Зоммерфельда [14].

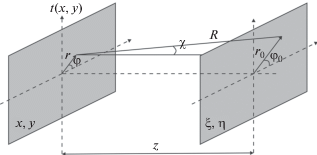
Пусть пучок излучения $E(0,x,y),$ распространяющийся от некоторого источника, падает слева на транспарант $t(x,y),$ тогда распределение амплитуды поля в плоскости наблюдения $E(z,\xi ,\eta )$ может быть представлено в виде:

где $\lambda $ – длина волны, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число, $R$ – расстояние до точки наблюдения.

Используя параксиальное приближение z $ \gg $ x, y, ξ, η разложим $R$ в ряд Тейлора

В фазовом множителе экспоненты, однако, малыми членами пренебречь нельзя, так как малые поправки умножаются на большую величину – волновое число, что привело бы к значительным ошибкам. Перепишем интеграл Релея–Зоммерфельда в приближении Френеля в виде свертки двух функций

где $u\left( {x,y} \right) = E\left( {0,x,y} \right) \cdot t\left( {x,y} \right)$ и $h\left( {z,x - \xi ,y - \eta } \right)$ = = ${{e}^{{ik\frac{{{{{\left( {x - \xi } \right)}}^{2}} + {{{\left( {y - \eta } \right)}}^{2}}}}{{2z}}}}}{{{{e}^{{ikz}}}} \mathord{\left/ {\vphantom {{{{e}^{{ikz}}}} z}} \right. \kern-0em} z}$ – функция импульсного отклика. Теорема о связи свертки и фурье-преобразования $F$ позволяет переписать это выражение в двух эквивалентных представлениях где $H\left( {{{\nu }_{x}},{{\nu }_{y}}} \right) = i\lambda \exp \left( {ikz} \right)$exp$\left[ {i\pi \lambda z\left( {\nu _{x}^{2} + \nu _{y}^{2}} \right)} \right]$ – фурье-образ $h\left( {z,x - \xi ,y - \eta } \right),$ а ${{\nu }_{x}}$ и ${{\nu }_{y}}$ – пространственные частоты.

Алгоритм расчета при помощи первого уравнения выражения (4) называется “методом импульсного отклика”, второго – “методом передаточной функции”. На первый взгляд может показаться, что лучше подставлять точное значение известной аналитической функции $H$, чем вычислять ее численно. Оказывается, из-за того что потом в любом случае необходимо выполнять обратное преобразование фурье, критическим моментом при выборе схемы расчета является способ осуществления дискретизации.

КРИТЕРИЙ ИСПОЛЬЗОВАНИЯ МЕТОДОВ

Единственной функцией, которая явно задана в выражении (4), является функция импульсного отклика, которая после исключения смещения на постоянное значение имеет вид $h\left( {z,x,y} \right)$ = = $\exp \left[ {ik{{\left( {{{x}^{2}} + {{y}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{x}^{2}} + {{y}^{2}}} \right)} {2z}}} \right. \kern-0em} {2z}}} \right]\exp {{\left( {ikz} \right)} \mathord{\left/ {\vphantom {{\left( {ikz} \right)} z}} \right. \kern-0em} z}.$ Из-за того, что значения функции с фазами $\delta \phi $ и $\delta \phi + 2\pi $ неотличимы, возникает явление, называемое фазовым элайзингом или “наложением порядков”. Для его исключения максимальное изменение фазы должно быть ограниченно

Для центрированной сетки значение ${{\left| x \right|}_{{max}}}$ равно половине расчетной сетки: ${{\left| x \right|}_{{max}}} = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}$ и, следовательно, получаем условие, при котором не возникают копии решения

С другой стороны, при использовании метода передаточной функции получается прямо противоположное условие. Проведем точно такие же рассуждения.

Воспользуемся одним из свойств быстрого преобразования Фурье: размер пространственной сетки связан с шагом частотной следующим образом $\Delta {{\nu }_{x}} = {1 \mathord{\left/ {\vphantom {1 L}} \right. \kern-0em} L},$ а максимальная частота равна частоте Найквиста ${{\nu }_{{Nyquist}}}$ = ${{\left| {{{\nu }_{x}}} \right|}_{{max}}}$ = ${1 \mathord{\left/ {\vphantom {1 {\left( {2\Delta x} \right)}}} \right. \kern-0em} {\left( {2\Delta x} \right)}}.$ Тогда подставляя эти величины в (7), получим

В случае равенства (6) и (8) оба метода работают одинаково [15].

Таким образом, попеременно меняя метод расчета, можно избежать явление фазового элайзинга, а полная численная схема, используемая в программе, выглядит следующим образом

РЕАЛИЗАЦИЯ ПРОГРАММЫ

Управление программой осуществляется с помощью одного из двух пользовательских интерфейсов. Первый является последовательно открывающейся системой окон, каждое из которых отвечает за определенный набор параметров. Например, интерфейс ввода параметров расчетной сетки и способа отображения конечных результатов работы программы представлен на рис. 2. После выбора всех параметров начинаются вычисления. Второй способ упрощает многократный ввод однотипных данных и позволяет задавать расчетные параметры, используя txt-файлы – “сценарии”. “Сценарий” – параметры моделирования, выстроенные в определенном порядке и записанные в txt-файл. Кроме указанных возможностей, опытный пользователь может создавать свои собственные оптические схемы, используя заложенный в программе набор функций. На данный момент программа способна смоделировать 25 типов элементов и 4 вида пучков. Результатом расчета является набор файлов, который может представлять собой распределение интенсивности или электрического поля, видеофайлы, графики, 3D-изображения.

В течение года программа широко использовалась при моделировании распространения пучков для многих оптических систем, использованных в экспериментах на НЛСЭ [3, 4, 6–10]: формировании с помощью дифракционных оптических элементов пучков различного модового состава (эрмит-гауссовы, лаггер-гауссовы пучки, бесселевы пучки с орбитальным угловым моментом), дифракции пучков на амплитудных и фазовых решетках, и т.п. Во всех случаях результаты экспериментов моделирования хорошо соответствовали друг другу. Среди этих исследований впервые выполненные эксперименты по дифракции бесселевых пучков с орбитальным угловым моментом (“закрученных пучков” [16]) на периодических решетках (аналог эффекта Тальбота) оказались наиболее интересными.

МОДЕЛИРОВАНИЕ ДИФРАКЦИИ БЕССЕЛЕВА ПУЧКА НА РЕШЕТКЕ КРУГЛЫХ ОТВЕРСТИЙ

Напомним основные свойства эффекта Тальбота – самовоспроизведение изображений периодической решетки, освещаемой монохроматической плоской волной [17]. Положения плоскостей самовоспроизведения для решетки с периодом $p$ определяются уравнением (10)

где $N$ и $n < m$ – натуральные числа, $p$ – период. При ограниченном размере решетки предельное значение $N$ ограничено областью взаимного пересечения дифрагирующих на решетке волн. В классическом случае в плоскостях, кратных ${{L}_{T}},$ возникает изображение отверстий исходной периодической структуры, а в дробных – их изображения с более высокой пространственной частотой, при этом диаметр изображений отверстий сохраняется.

Для n/m = 1/4 и 3/4 возникает изображение решетки с вдвое меньшим периодом, а для n/m = = 1/6, 1/3, 2/3, 5/6 и 3/4 – с втрое меньшим. Если n/m = ½, то в этих плоскостях, которые называются “половинными” плоскостями Тальбота (или “плоскостями 1/2”), мы будем наблюдать смещенное на половину пространственного периода изображение исходной структуры. В терагерцевом диапазоне классический эффект Тальбота был впервые продемонстрирован в [18].

Мы задались вопросом, что будет, если осветить решетку пучком с орбитальным угловым моментом? Хотя закрученные пучки активно используются уже четверть века, до настоящего времени их дифракция на двумерных периодических решетках не исследовалась. Очевидно, что при освещении периодической решетки закрученным пучком классический эффект Тальбота не может наблюдаться, и заранее было не ясно, какую картину мы будем наблюдать. Наши эксперименты [11] показали, что при освещении решетки бесселевыми пучками

где $\kappa $ – радиальное волновое число, а $\ell = 0, \pm 1, \pm 2{ \ldots }$ называют топологическим зарядом пучка, в плоскостях, соответствующих плоскостям Тальбота, вместо изображений отверстий наблюдаются кольца, т.е. исходный пучок преобразуется в “решетку” кольцевых микропучков. Из экспериментов стали понятны примерные зависимости свойств наблюдаемых колец от параметров эксперимента, но число экспериментов было ограничено, и для детального исследования эффекта он был смоделирован с помощью пакета WaveThruMasks.

Были проведены расчеты прохождения гауссова пучка через оптическую систему, состоящую из бинарного спирального аксикона, телескопа и амплитудной двумерной решетки круглых отверстий. Такая постановка задачи полностью имитирует эксперимент, схема которого представлена на рис. 3а. Падающий гауссов пучок вычисляется по формуле

где ${{w}_{0}}$ – модовый радиус, $z$ – расстояние от плоскости перетяжки, ${{k}_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число, ${{z}_{R}} = {{\pi w_{0}^{2}} \mathord{\left/ {\vphantom {{\pi w_{0}^{2}} \lambda }} \right. \kern-0em} \lambda }$ – длина Рэлея, ${{w}_{z}} = {{w}_{0}}\sqrt {{{\left( {{{z}^{2}} + z_{R}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {{{z}^{2}} + z_{R}^{2}} \right)} {z_{R}^{2}}}} \right. \kern-0em} {z_{R}^{2}}}} $ – полуширина пучка, $\zeta = \arctan \left( {{z \mathord{\left/ {\vphantom {z {{{z}_{R}}}}} \right. \kern-0em} {{{z}_{R}}}}} \right)$ – фаза Гуи, $r = \sqrt {{{x}^{2}} + {{y}^{2}}} $ – связь с декартовыми координатами.

В расчетах использовались сетка размером 4096 × 4096 элементов с размером пикселя 0.05 мм и гауссов пучок с плоским волновым фронтом (w₀ = 11 мм, z = 0 мм, $\lambda $ = 0.141 мм), что соответствовало условиям эксперимента. Транспарантом бинарного спирального аксикона является амплитудно-фазовый шаблон (рис. 3б), на котором черный цвет соответствует скачку фазы $\exp \left( {i\pi } \right),$ а белый – нулю. После применения алгоритма (9) на расстоянии $z$ = 200 мм от шаблона спирального аксикона в месте, где находится линза, формируется бесселев пучок с радиальным волновым числом $\kappa $ = 2 мм^–1. Детальное описание формирования бесселевых пучков бинарным аксиконом приведено в [19].

Поскольку получаемый пучок слишком мал для освещения достаточно числа отверстий периодической решетки, мы расширяем его с помощью телескопической системы с фокусными расстояниями элементов ${{f}_{1}} < {{f}_{2}}.$ Каждая “линза” моделируется обычным фазовым множителем $t\left( {x,y} \right)$ = $\exp \left( {ik{{\sqrt {{{x}^{2}} + {{y}^{2}}} } \mathord{\left/ {\vphantom {{\sqrt {{{x}^{2}} + {{y}^{2}}} } {2f}}} \right. \kern-0em} {2f}}} \right).$ В результате после прохождения телескопа бесселев пучок расширяется в $M = {{{{f}_{2}}} \mathord{\left/ {\vphantom {{{{f}_{2}}} {{{f}_{1}}}}} \right. \kern-0em} {{{f}_{1}}}}$ раз, а его радиальное волновое число уменьшается в $M$ раз. Расширенный бесселев пучок дифрагирует на амплитудной решетке круглых отверстий (рис. 3в), представляющей собой шаблон из нулей (черный – полное поглощение) и единиц (белый – пропускание).

В данной работе рассчитывались распределения электрического поля волны в плоскостях, соответствующих плоскостям самовоспроизведения периодической решетки в случае падения плоской волны (плоскостях Тальбота).

РЕЗУЛЬТАТ МОДЕЛИРОВАНИЯ

Некоторые результаты численного моделирования представлены на рис. 4 и 5. Во всех случаях, когда расчеты проводились при параметрах, для которых имелись экспериментальные результаты, они хорошо соответствовали друг другу (см. рис. 4б). Параметрические исследования (рис. 4 и 5) позволили сделать вывод, что кольцевые распределения, наблюдаемые в плоскостях Тальбота, зависят от периода, диаметра освещающего решетку пучка, номера плоскости Тальбота, а также от величины и знака топологического заряда.

Период решетки. Увеличение периода решетки $p$ (при фиксированных остальных параметрах) приводит к увеличению радиуса $R$ микропучков (рис. 4а и 5а), что символически можно записать как$p{\kern 1pt} \uparrow \, \to R{\kern 1pt} \uparrow {\text{.}}$

Диаметр бесселева пучка. При уменьшении диаметра освещающего пучка радиус колец увеличивается ${{\kappa {{f}_{1}}} \mathord{\left/ {\vphantom {{\kappa {{f}_{1}}} {{{f}_{2}}}}} \right. \kern-0em} {{{f}_{2}}}}{\kern 1pt} \uparrow \; \to \;R{\kern 1pt} \uparrow {\text{.}}$ При этом увеличение диаметра колец происходит до тех пор, пока соседние кольца не начнут накладываться друг на друга (см. рис. 4).

Топологический заряд. Радиус колец не зависит от величины топологического заряда$R = const(\ell ),$ а распределение фазы по азимуту соответствует топологическому заряду падающей волны (см. рис. 4а).

Плоскость Тальбота. Пространственная частота колец, получаемых при дифракции бесселева пучка на решетках круглых отверстий, совпадает с пространственной частотой изображений отверстий, наблюдаемых в случае освещения структур плоской волной (эффект Тальбота), однако радиус колец растет от плоскости к плоскости Тальбота $N{\kern 1pt} \uparrow \; \to \;R{\kern 1pt} \uparrow {\text{.}}$

Используя полученные зависимости и учитывая размерности величин, можно сконструировать ожидаемую зависимость радиуса микропучков от параметров задачи

Степени при $p$ и $\kappa $ соответствуют аппроксимации с помощью степенных функций (рис. 5). Экспериментальные ограничения не позволили нам исследовать картину дифракции в плоскостях $N > 1,$ поэтому мы оставляем обсуждение вида функции $F\left( {N,m,n} \right)$ на будущее.

ЗАКЛЮЧЕНИЕ

Описанный в данной работе пакет программ показал себя удобным инструментом для расчетов электромагнитного поля излучения, проходящего через систему амплитудно-фазовых транспарантов. Тестирование программы, выполненное путем сравнения результатов моделирования с результатами многочисленных экспериментов, выполненных на Новосибирском лазере на свободных электронах, продемонстрировало корректность вычислений в пределах применимости скалярной теории дифракции и их совпадение с экспериментальными результатами

Работа выполнена при поддержке гранта РНФ 14-50-00080. Авторы благодарны В.С. Черкасскому, написавшему первые варианты программы, моделирующей дифракцию пучков, многие идеи и советы которого были использованы при создании пакета, Н.А. Винокурову, И.А. Котельникову и Г.Н. Кулипанову за постоянные обсуждения данной задачи, а также Ю.Ю. Чопоровой и Н.Д. Осинцевой за участие в экспериментах и полезные дискуссии. Эксперименты выполнены с использованием оборудования Центра коллективного пользования, поддержанного Министерством образования и науки РФ (уникальный идентификатор проекта RFMEFI62117X0012).