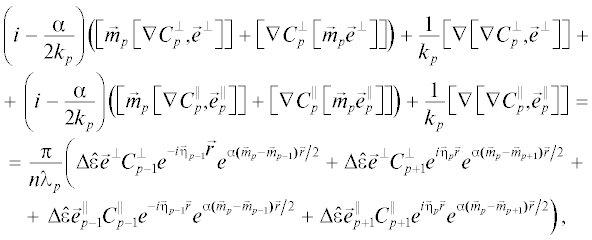Известия РАН. Серия физическая, 2019, T. 83, № 2, стр. 264-268
Уравнения связанных мод для акустооптической дифракции расходящегося светового пучка в поглощающей среде
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
Московский государственный университет имени М.В. Ломоносова
Москва, Россия
2 Федеральное государственное бюджетное учреждение науки
Научно-технологический центр уникального приборостроения РАН
Москва, Россия
* E-mail: nikitin.pavel.a@gmail.com
Аннотация
Исследовано акустооптическое взаимодействие в оптически изотропных средах. Получены векторные дифференциальные уравнения, описывающие дифракцию света на ультразвуке в поглощающей среде в режиме Рамана–Ната. Особое внимание уделено учету расходимости пучка излучения вследствие его поперечной ограниченности.
ВВЕДЕНИЕ
Для описания акустооптического (АО) взаимодействия необходимо решить уравнения Максвелла с диэлектрической проницаемостью, зависящей от координаты. В зависимости от используемых приближений можно выделить следующие известные модели АО-взаимодействия в прозрачной среде: 1) одномерная, справедливая для небольших углов отклонения дифрагированного излучения и имеющая простое аналитическое решение [1]; 2) двумерная, описывающая АО-дифракцию в режимах Брэгга и Рамана–Ната и учитывающая поляризационные эффекты [2]; 3) трехмерная, справедливая для брэгговского АО-взаимодействия пучков, имеющих в поперечном сечении гауссовый профиль по интенсивности [3].
Эффект поглощения излучения в среде был учтен в двумерной модели АО-взаимодействия в работе [4]. Принципиальным ограничением этой модели является пренебрежение эффектом угловой расходимости излучения, который проявляется, например, в терагерцевом (ТГц) диапазоне, где длина волны составляет около 0.1 мм. Многие двулучепреломляющие АО-материалы, хорошо зарекомендовавшие себя в видимом диапазоне, например, ниобат лития (LiNbO3) и парателлурит (TeO2) непрозрачны в ТГц-диапазоне [5, 6]. Поэтому работа посвящена исследованию АО-дифракции в оптически изотропных средах, а целью является обобщение математического аппарата [4] на случай расходящегося излучения.
МЕТОДЫ РЕШЕНИЯ
В рамках модели предполагалось, что собственные волны поглощающей среды являются линейно поляризованными и характеризуются напряженностью электрического поля в виде $\vec {E} = \vec {e}{{e}^{{ - \vec {\alpha }\vec {r}{\text{/}}2}}}{{e}^{{i(\vec {k}\vec {r} - \omega t)}}},$ где $\vec {e}$ – единичный вектор поляризации, $\vec {k}$ – волновой вектор, $\omega $ – круговая частота, $\vec {r}$ – трехмерный радиус-вектор, t – время, $\vec {\alpha }$ – векторный коэффициент поглощения электромагнитной волны, зависящий от ее направления распространения и поляризации в двулучепреломлящей среде и сонаправленный с волновым вектором в оптически изотропной среде.
С использованием волновых уравнений для напряженности электрического поля $\vec {E}$ [7]:
(1)
$ - [\nabla [\nabla \vec {E}]] = {{c}^{{ - 2}}}{{\partial }^{2}}({{\hat {\varepsilon }\vec {E})} \mathord{\left/ {\vphantom {{\hat {\varepsilon }\vec {E})} {\partial {{t}^{2}}}}} \right. \kern-0em} {\partial {{t}^{2}}}},$были получены дисперсионные уравнения, связывающие параметры электромагнитной волны
с действительной $\hat {\varepsilon }{\text{'}}$ и мнимой  частями тензора диэлектрической проницаемости
частями тензора диэлектрической проницаемости 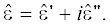
При выводе уравнений связанных мод была исследована дифракция Рамана–Ната и рассмотрены два основных режима, когда решение уравнения (1) можно представить в виде волн среды с амплитудами $C_{p}^{{||}}(\vec {r},t)$ и $C_{p}^{ \bot }(\vec {r},t)$ и ортогональными поляризациями $\vec {e}_{p}^{{||}}$ и ${{\vec {e}}^{ \bot }}{\text{:}}$
(2)
$\begin{gathered} \vec {E} = \sum\limits_{p = - \infty }^{ + \infty } {\left( {{{{\vec {e}}}^{ \bot }}\frac{{C_{p}^{ \bot }}}{{\sqrt n }}{{e}^{{ - {{{\vec {\alpha }}}_{p}}\vec {r}{\text{/}}2}}}{{e}^{{i({{{\vec {k}}}_{p}}\vec {r} - {{\omega }_{p}}t)}}}} \right.} + \\ + \,\,\left. {\vec {e}_{p}^{{||}}\frac{{C_{p}^{{||}}}}{{\sqrt n }}{{e}^{{ - {{{\vec {\alpha }}}_{p}}\vec {r}{\text{/}}2}}}{{e}^{{i({{{\vec {k}}}_{p}}\vec {r} - {{\omega }_{p}}t)}}}} \right) \\ \end{gathered} $и
(3)
$\vec {E} = \sum\limits_{p = - \infty }^{ + \infty } {\left( {{{{\vec {e}}}^{ \bot }}\frac{{C_{p}^{ \bot }}}{{\sqrt n }}{{e}^{{i({{{\vec {k}}}_{p}}\vec {r} - {{\omega }_{p}}t)}}} + \vec {e}_{p}^{{||}}\frac{{C_{p}^{{||}}}}{{\sqrt n }}{{e}^{{i({{{\vec {k}}}_{p}}\vec {r} - {{\omega }_{p}}t)}}}} \right)} ,$УРАВНЕНИЯ СВЯЗАННЫХ МОД
Подставив выражение $\vec {E} = \vec {e}{{e}^{{ - \vec {\alpha }\vec {r}/2}}}{{e}^{{i({\vec {k}}\vec {r} - \omega t)}}}$ для напряженности эклектического поля в волновое уравнение (1) и разделив мнимую и действительную части, можно получить соотношения, связывающие направления векторов $\vec {k}$, $\vec {e}$ и $\vec {\alpha }{\text{:}}$
Режим АО-дифракции Рамана–Ната характеризуется множеством дифракционных порядков, каждому из которых соответствует свой номер p. Следуя работе [2], введем: 1) единичные волновые векторы ${{\vec {m}}_{p}}$ и волновое число kp = = nωp/c, такие что ${{\vec {k}}_{p}} = {{k}_{p}}{{\vec {m}}_{p}};$ 2) векторы расстройки ${{\vec {\eta }}_{p}} = {{\vec {k}}_{{p + 1}}} - {{\vec {k}}_{p}} - \vec {K}$ и коэффициенты АО-связи:
(5)
$\begin{gathered} {{q}^{ \bot }} = \frac{\pi }{{n{{\lambda }_{p}}}}{\text{(}}{{{\vec {e}}}^{ \bot }}\Delta \hat {\varepsilon }{{{\vec {e}}}^{ \bot }}); \\ q_{p}^{{||}} = \frac{\pi }{{n{{\lambda }_{p}}}}{\text{(}}\vec {e}_{p}^{{||}}\Delta \hat {\varepsilon }\vec {e}_{{p + 1}}^{{||}});\,\,\,\,q_{p}^{{ \bot ||}} = \frac{\pi }{{n{{\lambda }_{p}}}}{\text{(}}{{{\vec {e}}}^{ \bot }}\Delta \hat {\varepsilon }\vec {e}_{p}^{{||}}). \\ \end{gathered} $Если среда оптически изотропная, то в каждом дифракционном порядке, соответствующем волновому вектору ${{\vec {k}}_{p}}{\text{:}}$ 1) справедливо соотношение ${{\vec {\alpha }}_{p}} = {{\vec {m}}_{p}}{\alpha ;}$ 2) электромагнитное поле можно разложить на две компоненты с ортогональными поляризациями, одна из которых $\vec {e}_{p}^{{||}}$ лежит в плоскости АО взаимодействия (в которой лежат волновые вектора ${{\vec {k}}_{p}}$), а ${{\vec {e}}^{ \bot }}$ – ортогональна этой плоскости, причем $\left| {\vec {e}_{p}^{{||}}} \right| = \left| {{{{\vec {e}}}^{ \bot }}} \right| = 1.$
Пусть в среде задано произвольное акустическое поле, вызывающее возмущение диэлектрической проницаемости $\Delta \hat {\varepsilon }(\vec {r})\cos (\vec {K}\vec {r} - \Omega t),$ где $\vec {K}$ и Ω – волновой вектор и круговая частота ультразвука, $\Delta \hat {\varepsilon }$ – симметричный тензор с вещественными компонентами. Для выполнения условия стационарности необходимо, чтобы разность частот электромагнитных волн в соседних порядках была постоянной и выполнялось условие ${{\omega }_{p}} = {{\omega }_{0}} + p\Omega $ для частоты электромагнитной волны в p-порядке.
Подставим (2) в волновое уравнение (1) с диэлектрической проницаемостью  + + $\Delta \hat {\varepsilon }(\vec {r})\cos (\vec {K}\vec {r} - \Omega t)$ и используем соотношения (4). Составляющая уравнения (1), осциллирующая с частотой ${{\omega }_{p}},$ имеет вид:
+ + $\Delta \hat {\varepsilon }(\vec {r})\cos (\vec {K}\vec {r} - \Omega t)$ и используем соотношения (4). Составляющая уравнения (1), осциллирующая с частотой ${{\omega }_{p}},$ имеет вид:
Таким образом, АО-дифракция на произвольном акустическом поле в поглощающей среде описывается системой векторных дифференциальных уравнений (уравнений связанных мод), пронумерованных по p от $ - \infty $ до $ + \infty ,$ причем p‑уравнение имеет вид (6). Как известно из дифракционной оптики, искривление волнового фронта вследствие расходимости пучка излучения описывается слагаемыми, содержащими вторую производную поля по координате [7]. В уравнении (6) эти слагаемые имеют вид $[\nabla {\text{[}}\nabla C\vec {e}{\text{]}}].$
По аналогии с работами [2, 4] найдем проекцию отдельных составляющих уравнения (6) на векторы поляризации ${{\vec {e}}^{ \bot }}$ и $\vec {e}_{p}^{{||}},$ учитывая, что $[\nabla {\text{[}}\nabla C,\vec {e}{\text{]}}] = (\vec {e}\nabla )\nabla C - \vec {e}\Delta C,$ используя известное выражение для двойного векторного произведения $[\vec {a}{\text{[}}\vec {b}\vec {c}{\text{]}}] = \vec {b}(\vec {a}\vec {c}) - \vec {c}(\vec {a}\vec {b})$ и принимая во внимание взаимную ортогональность векторов ${{\vec {e}}^{ \bot }}$, $\vec {e}_{p}^{{||}}$ и ${{\vec {m}}_{p}}{\text{:}}$
(7)
${{\vec {e}}^{ \bot }}\left( {[{{{\vec {m}}}_{p}}{\text{[}}\nabla C_{p}^{ \bot }{\text{,}}{{{\vec {e}}}^{ \bot }}{\text{]}}] + [\nabla C_{p}^{ \bot }{\text{[}}{{{\vec {m}}}_{p}}{{{\vec {e}}}^{ \bot }}{\text{]}}]} \right) = - 2({{\vec {m}}_{p}}\nabla )C_{p}^{ \bot },$(8)
$\vec {e}_{p}^{{||}}\left( {[{{{\vec {m}}}_{p}}{\text{[}}\nabla C_{p}^{{||}}{\text{,}}\vec {e}_{p}^{{||}}{\text{]}}] + [\nabla C_{p}^{{||}}{\text{[}}{{{\vec {m}}}_{p}}\vec {e}_{p}^{{||}}{\text{]}}]} \right) = - 2({{\vec {m}}_{p}}\nabla )C_{p}^{{||}},$(9)
$\begin{gathered} {{{\vec {e}}}^{ \bot }}\left( {[{{{\vec {m}}}_{p}}{\text{[}}\nabla C_{p}^{{||}}{\text{,}}\vec {e}_{p}^{{||}}{\text{]}}] + [\nabla C_{p}^{{||}}{\text{[}}{{{\vec {m}}}_{p}}\vec {e}_{p}^{{||}}{\text{]}}]} \right) = \\ = \vec {e}_{p}^{{||}}\left( {[{{{\vec {m}}}_{p}}{\text{[}}\nabla C_{p}^{ \bot }{\text{,}}{{{\vec {e}}}^{ \bot }}{\text{]}}] + [\nabla C_{p}^{ \bot }{\text{[}}{{{\vec {m}}}_{p}}{{{\vec {e}}}^{ \bot }}{\text{]}}]} \right) = 0, \\ \end{gathered} $(10)
$\begin{gathered} {{{\vec {e}}}^{ \bot }}\left( {[\nabla {\text{[}}\nabla C_{p}^{ \bot }{\text{,}}{{{\vec {e}}}^{ \bot }}{\text{]}}] + [\nabla {\text{[}}\nabla C_{p}^{ \bot }{\text{,}}\vec {e}_{p}^{{||}}{\text{]}}]} \right) = \\ = {{({{{\vec {e}}}^{ \bot }}\nabla )}^{2}}C_{p}^{ \bot } - \Delta C_{p}^{ \bot } + ({{{\vec {e}}}^{ \bot }}\nabla )(\vec {e}_{p}^{{||}}\nabla )C_{p}^{{||}}, \\ \end{gathered} $(11)
$\begin{gathered} \vec {e}_{p}^{{||}}\left( {[\nabla {\text{[}}\nabla C_{p}^{ \bot }{\text{,}}{{{\vec {e}}}^{ \bot }}{\text{]}}] + [\nabla {\text{[}}\nabla C_{p}^{ \bot }{\text{,}}\vec {e}_{p}^{{||}}{\text{]}}]} \right) = \\ = {{(\vec {e}_{p}^{{||}}\nabla )}^{2}}C_{p}^{{||}} - \Delta C_{p}^{{||}} + ({{{\vec {e}}}^{ \bot }}\nabla )(\vec {e}_{p}^{{||}}\nabla )C_{p}^{ \bot }, \\ \end{gathered} $(12)
${{\vec {m}}_{p}}\left( {[{{{\vec {m}}}_{p}}{\text{[}}\nabla C_{p}^{ \bot }{\text{,}}{{{\vec {e}}}^{ \bot }}{\text{]}}] + [\nabla C_{p}^{ \bot }{\text{[}}{{{\vec {m}}}_{p}}{{{\vec {e}}}^{ \bot }}{\text{]}}]} \right) = ({{\vec {e}}^{ \bot }}\nabla )C_{p}^{ \bot },$(13)
${{\vec {m}}_{p}}\left( {[{{{\vec {m}}}_{p}}{\text{[}}\nabla C_{p}^{{||}}{\text{,}}\vec {e}_{p}^{{||}}{\text{]}}] + [\nabla C_{p}^{{||}}{\text{[}}{{{\vec {m}}}_{p}}\vec {e}_{p}^{{||}}{\text{]}}]} \right) = (\vec {e}_{p}^{{||}}\nabla )C_{p}^{{||}},$(14)
$\begin{gathered} {{{\vec {m}}}_{p}}\left( {[\nabla {\text{[}}\nabla C_{p}^{ \bot }{\text{,}}{{{\vec {e}}}^{ \bot }}{\text{]}}] + [\nabla {\text{[}}\nabla C_{p}^{ \bot }{\text{,}}\vec {e}_{p}^{{||}}{\text{]}}]} \right) = \\ = ({{{\vec {m}}}_{p}}\nabla )\left( {({{{\vec {e}}}^{ \bot }}\nabla )C_{p}^{ \bot } + (\vec {e}_{p}^{{||}}\nabla )C_{p}^{{||}}} \right). \\ \end{gathered} $Таким образом, мы приходим к системе уравнений (6), спроецированных на векторы ${{\vec {e}}^{ \bot }}$ и $\vec {e}_{p}^{{||}}{\text{:}}$
(15)
$\begin{gathered} \left( {1 + i\frac{{\alpha }}{{2{{k}_{p}}}}} \right)({{{\vec {m}}}_{p}}\nabla )C_{p}^{ \bot } + \frac{i}{{2{{k}_{p}}}}[{{({{{\vec {e}}}^{ \bot }}\nabla )}^{2}}C_{p}^{ \bot } - \Delta C_{p}^{ \bot } + ({{{\vec {e}}}^{ \bot }}\nabla )(\vec {e}_{p}^{{||}}\nabla )C_{p}^{{||}}] = \\ = \,\,i\frac{{{{q}^{ \bot }}}}{2}\left( {C_{{p - 1}}^{ \bot }{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p - 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}} + C_{{p + 1}}^{ \bot }{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p + 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}} \right) + \\ + \,\,i\frac{{q_{{p - 1}}^{{ \bot ||}}}}{2}C_{{p - 1}}^{{||}}{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p - 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}} + i\frac{{q_{{p + 1}}^{{ \bot ||}}}}{2}C_{{p + 1}}^{{||}}{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p + 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $(16)
$\begin{gathered} \left( {1 + i\frac{{\alpha }}{{2{{k}_{p}}}}} \right)({{{\vec {m}}}_{p}}\nabla )C_{p}^{{||}} + \frac{i}{{2{{k}_{p}}}}[{{(\vec {e}_{p}^{{||}}\nabla )}^{2}}C_{p}^{{||}} - \Delta C_{p}^{{||}} + ({{{\vec {e}}}^{ \bot }}\nabla )(\vec {e}_{p}^{{||}}\nabla )C_{p}^{ \bot }] = \\ = \,\,i\frac{{q_{p}^{{ \bot ||}}}}{2}\left( {C_{{p - 1}}^{ \bot }{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p - 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}} + C_{{p + 1}}^{ \bot }{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p + 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}} \right) + \\ + \,\,i\frac{{q_{{p - 1}}^{{||}}}}{2}C_{{p - 1}}^{{||}}{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p - 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}} + i\frac{{q_{p}^{{||}}}}{2}C_{{p + 1}}^{{||}}{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p + 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $а также на вектор ортогональный ${{\vec {e}}^{ \bot }}$ и $\vec {e}_{p}^{{||}},$ т.е. на ${{\vec {m}}_{p}}{\text{:}}$
(17)
$\begin{gathered} \left( {i - \frac{{\alpha }}{{2{{k}_{p}}}} + \frac{1}{{{{k}_{p}}}}({{{\vec {m}}}_{p}}\nabla )} \right)[({{{\vec {e}}}^{ \bot }}\nabla )C_{p}^{ \bot } + (\vec {e}_{p}^{{||}}\nabla )C_{p}^{{||}}] = \\ = \,\,\delta _{p}^{ \bot }C_{{p - 1}}^{ \bot }{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p - 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}} + \delta _{p}^{ \bot }C_{{p + 1}}^{ \bot }{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p + 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}} + \\ + \,\,\delta _{{p,p - 1}}^{{||}}C_{{p - 1}}^{{||}}{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p - 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}} + \delta _{{p,p + 1}}^{{||}}C_{{p + 1}}^{{||}}{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}{{e}^{{{\alpha }({{{\vec {m}}}_{p}} - {{{\vec {m}}}_{{p + 1}}}){{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $(18)
$\delta _{p}^{ \bot } = \frac{\pi }{{n{{\lambda }_{p}}}}\left( {{{{\vec {m}}}_{p}}\Delta \hat {\varepsilon }{{{\vec {e}}}^{ \bot }}} \right);\,\,\,\delta _{{p,d}}^{{||}} = \frac{\pi }{{n{{\lambda }_{p}}}}\left( {{{{\vec {m}}}_{p}}\Delta \hat {\varepsilon }\vec {e}_{d}^{{||}}} \right).$Следует отметить, что в некоторых случаях, например, при обратной коллинеарной дифракции, множитель $\exp ( - \vec {\alpha }\vec {r})$ отсутствует в аналитическом решении уравнений связанных мод [8]. Поэтому, чтобы перейти от соотношения (2) к (3), необходимо сделать замену переменных $C_{p}^{ \bot } = C_{p}^{{ \bot \left( * \right)}}\exp ({\alpha }{{\vec {m}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2})$ и $C_{p}^{{||}}$ = $C_{p}^{{||\left( * \right)}}\exp ({\alpha }{{\vec {m}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2})$ и для удобства опустить индексы звездочки $C_{p}^{{ \bot (*)}}$ = $C_{p}^{ \bot }$ и $C_{p}^{{||(*)}} = C_{p}^{{||}}.$
После указанной замены переменных в уравнениях (15)–(17) были вычислены следующие градиенты:
(19)
$\left( {{{{\vec {m}}}_{p}}\nabla } \right)\left( {{{C}_{p}}{{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}} \right) = {{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}\left[ {\left( {{{{\vec {m}}}_{p}}\nabla } \right){{C}_{p}} + \frac{{\alpha }}{2}{{C}_{p}}} \right],$(20)
$\left( {\vec {e}\nabla } \right)\left( {{{C}_{p}}{{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}} \right) = {{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}\left( {\vec {e}\nabla } \right){{C}_{p}},$(21)
$\begin{gathered} ({{{\vec {m}}}_{p}}\nabla )\left( {\vec {e}\nabla } \right)\left( {{{C}_{p}}{{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}} \right) = \\ = {{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}\left( {\frac{{\alpha }}{2} + ({{{\vec {m}}}_{p}}\nabla )} \right)(\vec {e}\nabla ){{C}_{p}}, \\ \end{gathered} $(22)
$\left( {{{{\vec {e}}}^{ \bot }}\nabla } \right)\left( {\vec {e}_{p}^{{||}}\nabla } \right)\left( {{{C}_{p}}{{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}} \right) = {{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}\left( {{{{\vec {e}}}^{ \bot }}\nabla } \right)\left( {\vec {e}_{p}^{{||}}\nabla } \right){{C}_{p}},$(23)
$\begin{gathered} \Delta \left( {{{C}_{p}}{{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}} \right) = \\ = \,\,{{e}^{{{\alpha }{{{\vec {m}}}_{p}}{{\vec {r}} \mathord{\left/ {\vphantom {{\vec {r}} 2}} \right. \kern-0em} 2}}}}\left[ {\Delta {{C}_{p}} + {\alpha }({{{\vec {m}}}_{p}}\nabla ){{C}_{p}} + \frac{{{{{\alpha }}^{2}}}}{4}{{C}_{p}}} \right]. \\ \end{gathered} $После подстановки соотношений (19)–(23) в уравнения (15) и (16) были получены проекции уравнений связанных мод на векторы ${{\vec {e}}^{ \bot }},$ $\vec {e}_{p}^{{||}}$ и ${{\vec {m}}_{p}}{\text{:}}$
(24)
$\begin{gathered} ({{{\vec {m}}}_{p}}\nabla )C_{p}^{ \bot } + \frac{{\alpha }}{2}C_{p}^{ \bot } + \frac{i}{{2{{k}_{p}}}}\left( {\frac{{{{{\alpha }}^{2}}}}{4}C_{p}^{ \bot } + {{{\left( {{{{\vec {e}}}^{ \bot }}\nabla } \right)}}^{2}}C_{p}^{ \bot } - \Delta C_{p}^{ \bot } + \left( {{{{\vec {e}}}^{ \bot }}\nabla } \right)\left( {\vec {e}_{p}^{{||}}\nabla } \right)C_{p}^{{||}}} \right) = \hfill \\ = i\frac{{{{q}^{ \bot }}}}{2}\left( {C_{{p - 1}}^{ \bot }{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}} + C_{{p + 1}}^{ \bot }{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}} \right) + i\frac{{q_{{p - 1}}^{{ \bot ||}}}}{2}C_{{p - 1}}^{{||}}{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}} + i\frac{{q_{{p + 1}}^{{ \bot ||}}}}{2}C_{{p + 1}}^{{||}}{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}, \hfill \\ \end{gathered} $(25)
$\begin{gathered} ({{{\vec {m}}}_{p}}\nabla )C_{p}^{{||}} + \frac{{\alpha }}{2}C_{p}^{{||}} + \frac{i}{{2{{k}_{p}}}}\left( {\frac{{{{{\alpha }}^{2}}}}{4}C_{p}^{{||}} + {{{(\vec {e}_{p}^{{||}}\nabla )}}^{2}}C_{p}^{{||}} - \Delta C_{p}^{{||}} + ({{{\vec {e}}}^{ \bot }}\nabla )(\vec {e}_{p}^{{||}}\nabla )C_{p}^{ \bot }} \right) = \\ = i\frac{{q_{p}^{{ \bot ||}}}}{2}\left( {C_{{p - 1}}^{ \bot }{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}} + C_{{p + 1}}^{ \bot }{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}} \right) + i\frac{{q_{{p - 1}}^{{||}}}}{2}C_{{p - 1}}^{{||}}{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}} + i\frac{{q_{p}^{{||}}}}{2}C_{{p + 1}}^{{||}}{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}, \\ \end{gathered} $(26)
$\begin{gathered} \left( {i + \frac{1}{{{{k}_{p}}}}({{{\vec {m}}}_{p}}\nabla )} \right)\left[ {\left( {{{{\vec {e}}}^{ \bot }}\nabla } \right)C_{p}^{ \bot } + \left( {\vec {e}_{p}^{{||}}\nabla } \right)C_{p}^{{||}}} \right] = \\ = \delta _{p}^{ \bot }\left( {C_{{p - 1}}^{ \bot }{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}} + C_{{p + 1}}^{ \bot }{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}} \right) + \delta _{{p,p - 1}}^{{||}}C_{{p - 1}}^{{||}}{{e}^{{ - i{{{\vec {\eta }}}_{{p - 1}}}\vec {r}}}} + \delta _{{p,p + 1}}^{{||}}C_{{p + 1}}^{{||}}{{e}^{{i{{{\vec {\eta }}}_{p}}\vec {r}}}}. \\ \end{gathered} $Поскольку волновой вектор звука и волновые векторы электромагнитных волн лежат в одной плоскости, называемой плоскостью АО-взаимодействия, уравнения связанных мод удается записать и в координатном представлении. Введем прямоугольную систему координат Oxyz таким образом, чтобы:
1) единичные волновые векторы электромагнитных волн ${{\vec {m}}_{p}} = \{ \cos {{\theta }_{p}},\sin {{\theta }_{p}},0\} $ лежали в плоскости Oxy, где θp – угол, задающий направление распространения излучения в p-порядке дифракции;
2) волновой вектор звука $\vec {K} = K\{ 0,1,0\} $ был сонаправлен с осью Oy;
3) один из векторов поляризации ${{\vec {e}}^{ \bot }} = \{ 0,0,1\} $ был параллелен оси Oz, а второй $\vec {e}_{p}^{{||}} = \{ - \sin {{\theta }_{p}},\cos {{\theta }_{p}},0\} $ лежал в плоскости Oxy.
Пусть размер области АО-взаимодействия характеризуется длиной L. Тогда можно использовать следующие безразмерные координаты:
(27)
${{\xi }_{1}} = {x \mathord{\left/ {\vphantom {x L}} \right. \kern-0em} L},\,\,\,\,{{\xi }_{2}} = {y \mathord{\left/ {\vphantom {y L}} \right. \kern-0em} L},\,\,\,\,{{\xi }_{3}} = {z \mathord{\left/ {\vphantom {z L}} \right. \kern-0em} L},$а также безразмерные параметры:
(28)
$\begin{gathered} X = {\alpha }L,\,\,\,\,{{Y}^{{(*)}}} = {{q}^{{(*)}}}L,\,\,\,\,{{A}_{p}} = {{\alpha } \mathord{\left/ {\vphantom {{\alpha } {{{k}_{p}}}}} \right. \kern-0em} {{{k}_{p}}}}, \\ {{D}^{{(*)}}} = {{\delta }^{{(*)}}}L,\,\,\,\,{{G}_{p}} = {{k}_{p}}L, \\ \end{gathered} $(29)
$\begin{gathered} {{Z}_{p}} = ({{k}_{{p + 1}}}\cos {{\theta }_{{p + 1}}} - {{k}_{p}}\cos {{\theta }_{p}})L{{\xi }_{1}} + \\ + \,\,({{k}_{{p + 1}}}\sin {{\theta }_{{p + 1}}} - {{k}_{p}}\sin {{\theta }_{p}} - K)L{{\xi }_{2}}, \\ \end{gathered} $Подставив соотношения (27)–(29) и выражения для волновых векторов и векторов поляризации в уравнения (24)–(26), получим:
(30)
$\begin{gathered} \left( {\cos {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{1}}}} + \sin {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{2}}}}} \right)C_{p}^{ \bot } + \frac{X}{2}\left( {1 + i\frac{{{{A}_{p}}}}{4}} \right)C_{p}^{ \bot } - \frac{i}{{2{{G}_{p}}}}\left[ {\frac{{{{\partial }^{2}}}}{{\partial \xi _{1}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial \xi _{2}^{2}}}} \right]C_{p}^{ \bot } + \\ + \,\,\frac{i}{{2{{G}_{p}}}}\frac{\partial }{{\partial {{\xi }_{3}}}}\left( {\cos {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{2}}}} - \sin {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{1}}}}} \right)C_{p}^{{||}} = \\ = \,\,i\frac{{{{Y}^{ \bot }}}}{2}\left( {C_{{p - 1}}^{ \bot }{{e}^{{ - i{{Z}_{{p - 1}}}}}} + C_{{p + 1}}^{ \bot }{{e}^{{i{{Z}_{p}}}}}} \right) + i\frac{{Y_{{p - 1}}^{{ \bot ||}}}}{2}C_{{p - 1}}^{{||}}{{e}^{{ - i{{Z}_{{p - 1}}}}}} + i\frac{{Y_{{p + 1}}^{{ \bot ||}}}}{2}C_{{p + 1}}^{{||}}{{e}^{{i{{Z}_{p}}}}}, \\ \end{gathered} $(31)
$\begin{gathered} \left( {\cos {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{1}}}} + \sin {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{2}}}}} \right)C_{p}^{{||}} + \frac{X}{2}\left( {1 + i\frac{{{{A}_{p}}}}{4}} \right)C_{p}^{{||}} - \\ - \,\,\frac{i}{{2{{G}_{p}}}}\left[ {{{{\left( {\cos {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{1}}}} + \sin {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{2}}}}} \right)}}^{2}} + \frac{{{{\partial }^{2}}}}{{\partial \xi _{3}^{2}}}} \right]C_{p}^{{||}} + \\ + \,\,\frac{i}{{2{{G}_{p}}}}\frac{\partial }{{\partial {{\xi }_{3}}}}\left( {\cos {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{2}}}} - \sin {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{1}}}}} \right)C_{p}^{ \bot } = \\ = \,\,i\frac{{Y_{p}^{{ \bot ||}}}}{2}\left( {C_{{p - 1}}^{ \bot }{{e}^{{ - i{{Z}_{{p - 1}}}}}} + C_{{p + 1}}^{ \bot }{{e}^{{i{{Z}_{p}}}}}} \right) + i\frac{{Y_{{p - 1}}^{{||}}}}{2}C_{{p - 1}}^{{||}}{{e}^{{ - i{{Z}_{{p - 1}}}}}} + i\frac{{Y_{{p + 1}}^{{||}}}}{2}C_{{p + 1}}^{{||}}{{e}^{{i{{Z}_{p}}}}}, \\ \end{gathered} $(32)
$\begin{gathered} \left[ {i + \frac{1}{{{{G}_{p}}}}\left( {\cos {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{1}}}} + \sin {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{2}}}}} \right)} \right]\left[ {\frac{\partial }{{\partial {{\xi }_{3}}}}C_{p}^{ \bot } + \left( {\cos {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{2}}}} - \sin {{\theta }_{p}}\frac{\partial }{{\partial {{\xi }_{1}}}}} \right)C_{p}^{{||}}} \right] = \\ = \,\,D_{p}^{ \bot }\left( {C_{{p - 1}}^{ \bot }{{e}^{{ - i{{Z}_{{p - 1}}}}}} + C_{{p + 1}}^{ \bot }{{e}^{{i{{Z}_{p}}}}}} \right) + D_{{p,p - 1}}^{{||}}C_{{p - 1}}^{{||}}{{e}^{{ - i{{Z}_{{p - 1}}}}}} + D_{{p,p + 1}}^{{||}}C_{{p + 1}}^{{||}}{{e}^{{i{{Z}_{p}}}}}. \\ \end{gathered} $Система уравнений (30)–(32) является координатным представлением уравнений связанных мод, позволяя рассчитывать значения комплексных амплитуд $C_{p}^{ \bot }$ и $C_{p}^{{||}}$ на координатной сетке.
ОБСУЖДЕНИЕ
Отметим, что в практически важных случаях поглощение излучения достаточно слабое и ${{A}_{p}} \ll 1.$ Это допущение оправдано, так как в противном случае (${\alpha } \cong k$) эффективность дифракции чрезвычайно низка из-за малой длины эффективного АО-взаимодействия $L \propto {1 \mathord{\left/ {\vphantom {1 {\alpha }}} \right. \kern-0em} {\alpha }} \cong \lambda $ [8]. Если кроме этого пренебречь расходимостью электромагнитного излучения, то в левой части уравнений (24) и (25) останутся только два первых слагаемых, а левой части уравнений (31) и (32) – первые три. Таким образом, в предельном переходе, соответствующем одномерной модели АО дифракции плоской монохроматической волны в слабо поглощающей среде, уравнения (24) и (25) переходят в уравнения, полученные в работах [4, 8].
Полученные уравнения связанных мод имеют ограничение на отсутствие двулучепреломления. Кроме того, использованные выражения для напряженности электрического поля описывают электромагнитную волну как линейно поляризованную, что возможно только при слабой расходимости излучения.
ЗАКЛЮЧЕНИЕ
Получена система уравнений связанных мод, как в наиболее общем безкоординатном виде, так и в координатном представлении, наиболее удобном для расчетов, так как направления осей используемой системы координат связаны с плоскостью АО-взаимодействия.
Работа выполнена при поддержке гранта РНФ 18-12-00430.
Список литературы
Royer D., Dieulesaint E. Elastic waves in solids II: generation, acousto-optic interaction, applications. Berlin: Springer, 2000. 446 p.
Dyakonov E.A., Voloshinov V.B. // J. Commun. Technol. and Electron. 2014. V. 59. № 5. P. 456.
Parygin V.N. et al. // Proc. SPIE. 1998. V. 3581. P. 48.
Nikitin P.A., Voloshinov V.B. // Memoirs of the Faculty of Phys. 2016. V. 6. P. 166601.
Unferdorben M. et al. // J. Infrared, Millimeter, and Terahertz Waves. 2015. V. 36. № 12. P. 1203.
Unferdorben M. et al. // J. Infrared, Millimeter, and Terahertz Waves. 2016. V. 37. № 7. P. 703.
Trager F. Handbook of Lasers and Optics. Berlin: Springer, 2012. 1694 p.
Nikitin P.A., Voloshinov V.B. // Phys. proc. 2015. V. 70. P. 712.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая