Известия РАН. Серия физическая, 2019, T. 83, № 8, стр. 1143-1145
Плазменные неустойчивости, генерируемые космическими лучами в предфронте бесстолкновительной ударной волны
А. М. Быков 1, 2, *, С. М. Осипов 1
1 Федеральное государственное бюджетное учреждение науки Физико-технический институт
имени А.Ф. Иоффе Российской академии наук
Санкт-Петербург, Россия
2 Федеральное государственное автономное образовательное учреждение высшего образования
“Санкт-Петербургский политехнический университет Петра Великого”
Санкт-Петербург, Россия
* E-mail: byk@astro.ioffe.ru
Поступила в редакцию 10.10.2018
После доработки 20.02.2019
Принята к публикации 26.04.2019
Аннотация
Неравновесные распределения космических лучей (КЛ), ускоренных по механизму Ферми в предфронте ударной волны, формируются за счет рассеяния на флуктуациях магнитного поля. Кинетическая энергия ударной волны передается КЛ, которые в свою очередь усиливают магнитную турбулентность. Рассмотрена коротковолновая плазменная неустойчивость в предфронте бесстолкновительной ударной волны, вызванная взаимодействием плазмы с космическими лучами.
ВВЕДЕНИЕ
Ускорение космических лучей (КЛ) сильными ударными волнами (УВ) сопровождается существенным усилением магнитной турбулентности. Наиболее эффективные механизмы усиления магнитного поля связаны с потоковой неустойчивостью КЛ, акустической неустойчивостью Друри и Фалле и нерезонансной токовой неустойчивостью Белла (см. обзоры [1–3]). Предполагается, что акустическая неустойчивость связана с наличием градиента давления ускоренных частиц в предфронте УВ и возмущением давления КЛ, а коротковолновая неустойчивость Белла связана с током ускоренных частиц относительно фоновой плазмы в предфронте [4, 5]. Распределение КЛ формируется в предфронте УВ при их ускорении, описываемом механизмом Ферми, за счет рассеяния на движущихся флуктуациях магнитного поля. В процессе ускорения в предфронте УВ формируется неравновесное распределение ускоренных частиц, обладающее током относительно фоновой плазмы и градиентом давления, которые связанны друг с другом.
В данной работе мы на основе уравнений, описывающих поведение КЛ и фоновой плазмы в предфронте бесстолкновительной УВ (полученных в работе [6]), исследуем рост коротковолновых возмущений на фоне крупномасштабного состояния системы, состоящей из ускоренных частиц и фоновой плазмы, формирующегося в процессе рассеяния частиц и их ускорения в предфронте УВ. Особенность данного рассмотрения заключается в согласованном учете и градиента давления КЛ, и их тока. Найдены показатели роста новых растущих мод.
ДИССПЕРСИОНОЕ СООТНОШЕНИЕ КОРОТКОВОЛНОВОЙ НЕУСТОЙЧИВОСТИ
Рассмотрим систему уравнений, описывающую плазму в предфронте бесстолкновительной ударной волны, состоящую из холодных фоновых протонов и электронов, а также частиц, ускоренных до высоких энергий. Плазма в целом предполагается квазинейтральной. Для описания динамики плазмы в предфронте используем уравнения, полученные в работе [6]
(1)
$\begin{gathered} \rho \left( {\frac{{\partial{ \vec {u}}}}{{\partial t}} + \left( {\vec {u}\nabla } \right)\vec {u}} \right) = - \nabla {{p}_{g}} + \frac{1}{{4\pi }}\left( {\nabla \times \vec {B}} \right) \times \\ \times \,\,\vec {B} - \frac{1}{c}\left( {{{{\vec {j}}}^{{cr}}} - e{{n}_{{cr}}}\vec {u}} \right) \times \vec {B} - \int {\vec {p}I\left[ f \right]{{d}^{3}}p,} \\ \end{gathered} $(2)
$\begin{gathered} \frac{{\partial {{P}_{{\alpha }}}}}{{\partial t}} + {{\nabla }_{{\alpha }}}{{p}_{{cr}}} + {{\nabla }_{{\beta }}}{{\prod }_{{{\alpha \beta }}}} = \\ = {{\left[ {\frac{1}{c}\left( {{{{\vec {j}}}_{{cr}}} - e{{n}_{{cr}}}\vec {u}} \right) \times \vec {B} + \int {\vec {p}I\left[ f \right]{{d}^{3}}p} } \right]}_{{\alpha }}}. \\ \end{gathered} $Здесь ρ, $\vec {u},$ pg – плотность, скорость и давление фоновой плазмы соответственно, $\vec {B}$ – индукция магнитного поля, с – скорость света, $\vec {p},$ f, e, ncr, ${{\vec {j}}_{{cr}}},$ pcr, $\vec {P},$ ${{\prod }_{{{\alpha \beta }}}}$ – импульс, усредненная функция распределения, электрический заряд, плотность, электрический ток, давление, плотность потока импульса и тензор натяжений ускоренных частиц соответственно, I[f] – стохастический интеграл столкновений. При этом концентрация КЛ много меньше, чем фоновой плазмы.
Следуя работе [6], для описания рассеяния КЛ используем модельный интеграл столкновений в системе покоя фоновой плазмы, имеющий вид
где fiso – изотропная часть функции распределения ускоренных частиц, χ – частота столкновений. Рассматриваем возмущение индукции магнитного поля $\delta \vec {b}$ на фоне постоянного магнитного поля ${{\vec {B}}_{0}}.$ Также мы предполагаем, что $\chi = a\Omega ,$ где $\Omega $ = $\frac{{ec{{B}_{0}}}}{\varepsilon },$ a – постоянный параметр, ε – энергия ускоренной частицы. Используя выражение (3), получимв правых частях выражений (1) и (2).
Далее анализ роста возмущений проводим в коротковолновом пределе, по аналогии с работой [5]. В рассматриваемом пределе, когда длина волны возмущения много меньше длины свободного пробега ускоренной частицы $\frac{{k{v}}}{\chi } \gg 1,$ и ее гирорадиуса $\frac{{k{v}}}{\Omega } \gg 1,$ отклик функции распределения на возмущение магнитного поля мал (см. [5, 7]) и им можно пренебречь. Здесь v – модуль скорости ускоренной частицы, k – модуль волнового вектора возмущения. Поэтому можно пренебречь возмущением тока ускоренных частиц и интегралом столкновений для возмущений в уравнении (1), при этом невозмущенные вклады от ускоренных частиц учтены.
Запишем соотношение для невозмущенного состояния на основе уравнения (2) в системе покоя фоновой плазмы в виде
(5)
$\nabla {{p}_{{cr0}}} = \frac{1}{c}\vec {j}_{0}^{{cr}} \times {{\vec {B}}_{0}} + \int {\vec {p}I\left[ {{{f}_{0}}} \right]{{d}^{3}}p} ,$На основе выражений (1) и (5) получаем уравнение движения фоновой плазмы для малых возмущений в коротковолновой области в системе покоя невозмущенной фоновой плазмы
(6)
$\begin{gathered} \frac{{\partial \delta \vec {u}}}{{\partial t}} = - \frac{1}{{{{\rho }_{0}}}}\nabla \delta {{p}_{g}} + \frac{1}{{4\pi {{\rho }_{0}}}}\left( {\nabla \times \delta \vec {b}} \right) \times \\ \times \,\,{{{\vec {B}}}_{0}} - \frac{1}{{c{{\rho }_{0}}}}\vec {j}_{0}^{{cr}} \times \delta \vec {b} + \frac{{\delta \rho }}{{\rho _{0}^{2}}}\nabla {{p}_{{cr0}}}. \\ \end{gathered} $Здесь величины, содержащиеся в обозначении δ, соответствуют малым возмущениям на фоне невозмущенного состояния системы. Пренебрегаем градиентами невозмущенных величин, кроме слагаемого $\frac{{\delta \rho }}{{\rho _{0}^{2}}}\nabla {{p}_{{cr0}}}$ в уравнении (6). Заметим, что в работе [5] вместо слагаемого $\frac{{\delta \rho }}{{\rho _{0}^{2}}}\nabla {{p}_{{cr0}}}$ в уравнение (6) входила плотность силы $\frac{{\delta \rho }}{{\rho _{0}^{2}}}\vec {j}_{0}^{{cr}} \times {{\vec {B}}_{0}}.$
Далее из уравнения (6), уравнений неразрывности для фоновой плазмы и вмороженности магнитного поля в фоновую плазму, рассматривая возмущения в виде плоских волн, находим дисперсионное соотношение для усиливающихся мод в предфронте ударной волны. Соотношения между невозмущенными электрическим током и градиентом давления ускоренных частиц получим из уравнения (5).
Приведем частные случаи геометрии системы и направлений волнового вектора мод:
а) В продольной ударной волне орт ${{\vec {e}}_{x}}$ совпадает с направлением нормали к фронту ударной волны и направлением невозмущенного магнитного поля ${{\vec {B}}_{0}}.$ В данной геометрии в соответствии с (5) имеем $\nabla {{p}_{{cr0}}}$ = $ - \frac{{a{{B}_{0}}}}{c}j_{0}^{{cr}}{{\vec {e}}_{x}},$ $\vec {j}_{0}^{{cr}}$ = $j_{0}^{{cr}}{{\vec {e}}_{x}}.$ В случае продольного распространения, когда волновой вектор $\vec {k}$ параллелен вектору ${{\vec {B}}_{0}},$ имеем дисперсионные соотношения
где ${{v}_{a}}$ = $\frac{{{{B}_{0}}}}{{\sqrt {4\pi {{\rho }_{0}}} }},$ ${{v}_{s}}$ – скорость звука в фоновой плазме, ${{k}_{0}}$ = $\frac{{4\pi j_{{0x}}^{{cr}}}}{{c{{B}_{0}}}}.$ В предфронте ударной волны ток ускоренных частиц относительно фоновой плазмы, направленный вдоль нормали к фронту $j_{{0x}}^{{cr}}$ ≈ $e{{n}_{{cr}}}{{u}_{{sh}}},$ где ush – скорость ударной волны относительно фоновой плазмы. Дисперсионное соотношение (7) совпадает с результатом работ [4, 5], а моды из дисперсионного соотношения (8) связанны с градиентом давления ускоренных частиц.
б) В поперечной ударной волне орт ${{\vec {e}}_{x}}$ совпадает с направлением нормали к фронту ударной волны. Вектор ${{\vec {B}}_{0}}$ направлен вдоль орта ${{\vec {e}}_{z}}.$ В соответствии с (5) имеем $\nabla {{p}_{{cr0}}}$ = $ - \frac{{{{B}_{0}}j_{{0x}}^{{cr}}}}{c}\left( {a + \frac{1}{a}} \right){{\vec {e}}_{x}},$ $\vec {j}_{0}^{{cr}}$ = = $j_{{0x}}^{{cr}}\left( {{{{\vec {e}}}_{x}} - \frac{1}{a}{{{\vec {e}}}_{y}}} \right).$ Для различных возможных направлений волнового вектора получим
(9)
${{\omega }^{2}} = \left( {v_{a}^{2} + v_{s}^{2}} \right){{k}^{2}} - iav_{a}^{2}{{k}_{0}}k,\,\,\,{\text{при}}\,\,\,\vec {k} = k{{\vec {e}}_{x}},$(10)
${{\omega }^{2}} = \left( {v_{a}^{2} + v_{s}^{2}} \right){{k}^{2}} + iv_{a}^{2}{{k}_{0}}k,\,\,\,{\text{при}}\,\,\,\vec {k} = k{{\vec {e}}_{y}},$(11)
$\begin{gathered} {{\omega }^{2}} = \frac{1}{2}\left\{ {\left( {v_{a}^{2} + v_{s}^{2}} \right){{k}^{2}} \pm } \right. \\ \left. { \pm \,\,\sqrt {{{{\left( {v_{a}^{2} - v_{s}^{2}} \right)}}^{2}}{{k}^{4}} + 4v_{a}^{4}k_{0}^{2}{{k}^{2}}\left( {1 + \frac{1}{{{{a}^{2}}}}} \right)} } \right\}, \\ {\text{при}}\,\,\,\vec {k} = k{{{\vec {e}}}_{z}}. \\ \end{gathered} $Заметим, что для невозмущенного состояния системы, рассмотренного в [5], существуют усиливающиеся моды из (11), однако растущие моды из (9) и (10) отсутствуют. Они возникают при учете связи градиента давления КЛ и электрического тока КЛ в условии (5).
в) Для наклонной ударной волны в пределе ${{k}_{0}} \gg k$ существует новая растущая мода. На рис. 1 и 2 приведены показатели роста двух растущих мод. Мода на рис. 1 соответствует моде Белла [5], а новая растущая мода показана на рис. 2. Орт ${{\vec {e}}_{x}}$ здесь направлен по нормали к фронту ударной волны ${{\vec {B}}_{0}}$ = ${{B}_{0}}\left( {{{{\vec {e}}}_{x}}\cos \psi } \right.$ + $\left. {{{{\vec {e}}}_{z}}\sin \psi } \right).$
Рис. 1.
Зависимость показателя роста моды от направления волнового вектора в единицах ${{{v}}_{a}}\sqrt {{{k}_{0}}k} .$ При параметрах: a = 1, $\psi = \frac{\pi }{4}.$ Данная мода эквивалентна моде, полученной в работе [5]. Здесь ${{k}_{x}}$ = = $k\sqrt {1 - {{\mu }^{2}}} \cos \varphi ,$ ${{k}_{y}}$ = $k\sqrt {1 - {{\mu }^{2}}} \sin \varphi ,$ ${{k}_{z}} = k\mu .$

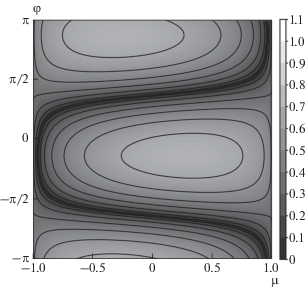
Рис. 2.
Зависимость показателя роста моды от направления волнового вектора в единицах ${{{v}}_{a}}\sqrt {{{k}_{0}}k} .$ При параметрах: a = 1, $\psi = \frac{\pi }{4}.$ Данная мода отсутствует в случае задания невозмущенного состояния системы, как в работе [5], где не учитывался градиент давления ускоренных частиц, согласованный с их электрическим током. Здесь ${{k}_{x}}$ = $k\sqrt {1 - {{\mu }^{2}}} \cos \varphi ,$ ${{k}_{y}}$ = = $k\sqrt {1 - {{\mu }^{2}}} \sin \varphi ,$ ${{k}_{z}} = k\mu .$
Работа поддержана программой Президиума РАН № 12 (проект Минобрнауки КП19-270). Результаты работы получены с использованием вычислительных ресурсов суперкомпьютерного центра СПбПУ им. Петра Великого (www.scc.spbstu.ru).
Список литературы
Blandfod R., Eichler D. // Phys. Rep. 1987. V. 154. P. 1.
Schure K., Bell A.R., Drury L.O., Bykov A.M. // Space Sci. Rev. 2012. V. 173. P. 491.
Markowith A., Bret A., Bykov A. et al. // Rep. Prog. Phys. 2016. V. 79. № 4. Art. № 046901.
Bell A.R. // MNRAS. 2004. V. 353. P. 550.
Bell A.R. // MNRAS. 2005. V. 358. P. 181.
Bykov A.M, Brandenburg A., Malkov M.A. et al. // Space Sci. Rev. 2013. V. 178. № 2–4. P. 201.
Bykov A.M., Osipov S.M., Ellison D.C. // MNRAS. 2011. V. 410. P. 39.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


