Известия РАН. Серия физическая, 2019, T. 83, № 9, стр. 1158-1168
Построение и классификация феноменологических моделей фазовых переходов методами теории катастроф
С. В. Павлов *
Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”
Москва, Россия
* E-mail: swcusp@mail.ru
Поступила в редакцию 12.11.2018
После доработки 29.03.2019
Принята к публикации 27.05.2019
Аннотация
Методами теории катастроф с использованием эквивариантных векторных полей, учитывающих симметрию термодинамической системы, построены феноменологические модели фазовых переходов для двух- и трехкомпонентных параметров порядка. Проведена классификация моделей по числу управляющих параметров, зависящих от внешних термодинамических условий. Построены фазовые диаграммы некоторых моделей и рассчитаны теоретические температурные зависимости тепловых свойств. Сопоставление теоретических и экспериментальных данных показало удовлетворительное качественное соответствие.
ВВЕДЕНИЕ
Феноменологическая теория фазовых переходов должна быть полностью основана на строгих математических методах. Теория групп позволяет на основе знания группы высокосимметричной фазы кристалла G0 перечислить все низкосимметричные фазы, в которые возможен фазовый переход, и для каждой фазы определить размерность параметров порядка. С помощью теории инвариантов вычисляются инвариантные комбинации компонент параметра порядка (базисные инварианты), от которых зависит термодинамический потенциал. Но для определения фазовых диаграмм и нахождения зависимостей физических свойств от внешних воздействий – температуры, давления и т.п. вблизи точек фазового перехода – нужно переходить к модельным представлениям. Любая физическая модель есть упрощенная версия физической системы, сохраняющая ее основные и главные черты. А основные черты термодинамической системы, испытывающей фазовый переход, – глобальная минимальность и структурная устойчивость. Для обеспечения термодинамической устойчивости системы потенциал не должен допускать бесконечно больших флуктуаций параметра порядка, приводящих к бесконечному выигрышу в энергии. Для этого требуется, чтобы термодинамический потенциал имел глобальный минимум при конечных значениях параметра порядка. Понятие структурной устойчивости для феноменологии фазовых переходов является одним из важнейших, поскольку в разряд физических явлений можно отнести лишь те, которые обладают достаточной повторяемостью в эксперименте. Значит, феноменологическая модель, описывающая свойства такой системы, должна быть структурно устойчива.
Явный вид термодинамического потенциала согласно теории Ландау [1] задается в виде конечного отрезка разложения в степенной ряд по инвариантным комбинациям параметров порядка. Глобальная минимальность обеспечивается тем, что члены высших степеней в разложении имеют четные степени и положительные коэффициенты. Условие структурной устойчивости всегда выполняется только в случае одного однокомпонентного параметра порядка. Для многокомпонентных параметров порядка структурную устойчивость моделей обеспечить удается далеко не всегда.
Применение методов теории катастроф делает возможным построение структурно устойчивых феноменологических моделей. При этом исходными данными служат только знание целого рационального базиса инвариантов (ЦРБИ) и число управляющих параметров, зависящих от внешних термодинамических величин (температуры, давления, химпотенциалов примесей и т.д.). И самое главное, такая постановка задачи позволяет проводить классификацию феноменологических моделей по числу управляющих параметров для данного набора базисных инвариантов. Целью данной работы является начало проведения такой классификации на основе построения структурно устойчивых моделей методами эквивариантной теории катастроф.
ОПИСАНИЕ МЕТОДА
Алгоритм построения феноменологических моделей методами теории катастроф с использованием эквивариантных векторных полей подробно изложен в работах [2, 3], поэтому затронем только ключевые моменты.
Представим термодинамический потенциал в окрестности точки фазового перехода, которая является вырожденной критической точкой [4, 5], в формальный ряд по степеням параметра порядка
(1)
$\Phi (\vec {\eta }) = \sum\limits_{q = 1}^\infty {{{a}_{q}}({{\alpha }_{1}},...{{\alpha }_{m}}){{{\vec {\eta }}}^{q}}} ,$Подходящей гладкой заменой переменных
можно удалить члены ряда, не влияющие на топологию фазовой диаграммы. При этом ряд
(2) должен обеспечивать взаимно однозначную замену переменных, что выполняется при
условии ${\text{det}}\left( {\frac{{\partial{ \vec {\eta }}}}{{\partial{ \vec {\xi }}}}} \right) \ne 0.$ Это можно сделать, считая, что ${{\left. {\frac{{\partial V}}{{\partial{ \vec {\xi }}}}} \right|}_{{\vec {\xi } = 0}}} = 0$ для малых $\vec {\xi },$ причем функция 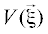 также представима в виде формального ряда с неопределенными пока коэффициентами.
Подставляя (2) в (1), разложим Ф в ряд по
также представима в виде формального ряда с неопределенными пока коэффициентами.
Подставляя (2) в (1), разложим Ф в ряд по  и учтем только линейный член:
и учтем только линейный член:
(3)
$\Phi \left( {\vec {\xi } + V{\text{(}}\vec {\xi }{\text{)}}} \right) = {\Phi (}\vec {\xi }{\text{)}} + \frac{{\partial {\Phi }}}{{\partial{ \vec {\xi }}}}V{\text{(}}\vec {\xi }{\text{)}}{\text{.}}$Если рассмотреть в (3) слагаемые степени k, то можно подобрать такие коэффициенты ряда $V{\text{(}}\vec {\xi }{\text{),}}$ которые обратят в нуль все слагаемые этой степени. При этом появятся новые слагаемые, которые перенормируют оставшиеся коэффициенты ряда Ф. Повторяя процедуру для степени k + 1 и выше, получаем итерационный процесс устранения всех степеней выше k.
Однако такой процесс, при всей его прозрачности, трудоемок и не учитывает симметрии параметра порядка. В конструктивном методе первые члены разложения (1) подбором параметров αi на основании теоремы о неявной функции [6] обращаются в нуль. Оставшиеся члены ряда (1) разбиваются на однородные или квазиоднородные части F = f0+ f1+ f2+ … степеней N, N + 1, N + + 2, … и на однородную или квазиоднородную часть наименьшей степени действуют эквивариантные векторные поля
(4)
${{V}_{k}} = \sum\limits_i {{{\nabla }_{i}}{{J}_{k}}\frac{\partial }{{\partial {{\eta }_{i}}}}} ,\,\,\,\,{\text{где }}{{\nabla }_{i}}{{J}_{k}} = \frac{{\partial {{J}_{k}}}}{{\partial {{\eta }_{i}}}}.$В результате находим члены ряда, принадлежащие градиентному идеалу ${{V}_{k}}{{f}_{0}} \in {{I}_{{\nabla {{f}_{0}}}}}.$ Если при этом не получаем конечной локальной алгебры, то процедуру повторяем для полей ${{V}_{{k1}}},$ которые определяются как линейные комбинации операторов ${{V}_{k}},$ причем ${{V}_{{k1}}}{{f}_{0}} = 0$ и ${{V}_{{k1}}}{{f}_{1}} \in {{I}_{{\nabla {{f}_{1}}}}}.$ Такой итерационный процесс дает в результате конечную локальную алгебру, которая вместе с мономами низших степеней и определяют топологию фазовой диаграммы для данного ЦРБИ и числа управляющих параметров.
Можно рассматривать эквивариантные векторные поля, зависящие только от базисных инвариантов [2, 3]:
(5)
${{U}_{k}} = \sum\limits_{m,i} {\left( {{{\nabla }_{i}}{{J}_{k}}{{\nabla }_{i}}{{J}_{m}}} \right)\frac{\partial }{{\partial {{J}_{m}}}}} ,$ФЕНОМЕНОЛОГИЧЕСКИЕ МОДЕЛИ С ДВУХКОМПОНЕНТНЫМ ПАРАМЕТРОМ ПОРЯДКА
Базисные инварианты, от которых зависит термодинамический потенциал, однозначно определяются с помощью так называемой L‑группы – группы, содержащей все различные матрицы неприводимого представления, по которому происходит фазовый переход [7]. Для двухкомпонентного параметра порядка L-группы изоморфны точечным (не обязательно кристаллографическим) группам симметрии Cnv и Cn (n = 3, 4, 6,…).
Базисные инварианты для групп L = Cnv представимы в общем виде:
а в пространстве базисных инвариантов – по формулам (5):
(6)
$\begin{gathered} {{U}_{1}} = 4{{J}_{1}}\frac{\partial }{{\partial {{J}_{1}}}} + 2n{{J}_{2}}\frac{\partial }{{\partial {{J}_{2}}}}, \\ {{U}_{2}} = 2n{{J}_{2}}\frac{\partial }{{\partial {{J}_{1}}}} + {{n}^{2}}J_{1}^{{n - 1}}\frac{\partial }{{\partial {{J}_{2}}}}. \\ \end{gathered} $Для дальнейших расчетов удобно произвести замену переменных (η1 η2) → (r, φ): $\eta = r{{e}^{{i\varphi }}}.$ Тогда ${{J}_{1}} = {{r}^{2}},$ ${{J}_{2}} = {{r}^{n}}\cos n\varphi .$
Рассмотрим в качестве примера построение феноменологической модели с группой симметрии параметра порядка L = C6v с тремя управляющими параметрами. В этом случае ЦРБИ для двухкомпонентного параметра порядка имеет вид
и эквивариантные векторные поля в пространстве базисных инвариантов определяются по формуле (6) с n = 6:
(7)
$\begin{gathered} {{U}_{1}} = 4{{J}_{1}}\frac{\partial }{{\partial {{J}_{1}}}} + 12{{J}_{2}}\frac{\partial }{{\partial {{J}_{2}}}}, \\ {{U}_{2}} = 12{{J}_{2}}\frac{\partial }{{\partial {{J}_{1}}}} + 36J_{1}^{5}\frac{\partial }{{\partial {{J}_{2}}}}. \\ \end{gathered} $Разложим термодинамический потенциал в ряд по степеням базисных инвариантов и выделим слагаемые, однородные по степеням параметра порядка. Тогда
(8)
$\begin{gathered} F = \underbrace {{{a}_{1}}{{J}_{1}}}_2 + \underbrace {{{a}_{2}}J_{1}^{2}}_4 + \underbrace {{{a}_{3}}J_{1}^{3} + {{a}_{4}}{{J}_{a}}}_6 + \\ + \,\,\underbrace {{{a}_{5}}J_{1}^{4} + {{a}_{6}}{{J}_{1}}{{J}_{2}}}_8 + .... \\ \end{gathered} $Под фигурными скобками указаны степени слагаемых по компонентам параметра порядка. Подходящим подбором параметров, варьируемых в эксперименте, можно положить a1 = a2 = a3 = 0 (такой подбор гарантируется теоремой о неявной функции [6]). Тогда из (8) следует, что однородная часть наименьшей степени шесть f0= J2. Подействуем на нее эквивариантными векторными полями (7):
(9)
${{U}_{1}}{{f}_{0}} = 12{{J}_{2}} \in {{I}_{{\nabla {{f}_{0}}}}},\,\,\,\,{{U}_{2}}{{f}_{0}} = 36J_{1}^{5} \in {{I}_{{\nabla {{f}_{0}}}}}.$Из (9) следует, что все мономы $J_{1}^{{{{k}_{1}}}}J_{2}^{{{{k}_{2}}}}$ с ${{k}_{1}} \geqslant 0,$ ${{k}_{2}} > 1,$ а также с ${{k}_{1}} \geqslant 5,$ ${{k}_{2}} \geqslant 0$ принадлежат идеалу, и безразмерный математический термодинамический потенциал с тремя управляющими параметрами имеет вид:
(10)
$F = {{a}_{1}}{{J}_{1}} + {{a}_{2}}J_{1}^{2} + {{a}_{3}}J_{1}^{3} + {{J}_{2}} + {{b}_{1}}J_{1}^{4}.$Последнее слагаемое в модели (10) не попало в градиентный идеал ${{I}_{{\nabla F}}}$ и коэффициент b1 в этом слагаемом не является управляющим параметром. В теории катастроф и теории особенностей дифференцируемых отображений такие коэффициенты называются модулями [2, 3, 6]. Модули отличаются от управляющих параметров тем, что не зависят от внешних термодинамических параметров и определяют только бифуркационный тип фазовой диаграммы. Этот результат не может быть получен без применения методов теории катастроф. В данном случае b1 > 0, что необходимо для обеспечения глобальной минимальности феноменологической модели (10).
Аналогичным образом строятся и другие феноменологические модели. Как видно из данного примера, для построения потребовалось только знание группы симметрии параметра порядка, определяющее ЦРБИ системы, и число управляющих параметров, варьируемых в эксперименте.
Построение феноменологических моделей фазовых переходов методами теории катастроф позволяет провести классификацию термодинамических потенциалов по числу управляющих параметров. В табл. 1–3 представлены феноменологические модели с двухкомпонентными параметрами порядка. Базисные инварианты имеют вид ${{J}_{1}} = {{r}^{2}},$ ${{J}_{2}} = {{r}^{n}}\cos n\varphi $ (n = 3, 4, 6), при этом η1 = r cos φ, η2 = r sin φ. Коэффициенты ai в таблицах – управляющие параметры, bi – модули.
Таблица 1.
Феноменологические модели с L = C3v
| c | F | μ |
|---|---|---|
| 1 | Нет модели | |
| 2 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + J_{1}^{2} + {{b}_{1}}J_{2}^{2}$ | 4 |
| 3 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2} + {{J}_{1}}{{J}_{2}} + {{b}_{1}}J_{2}^{2} + J_{1}^{3}$ | 5 |
| 4 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2} + {{a}_{4}}{{J}_{1}}{{J}_{2}} + \\ + \,\,{{b}_{1}}J_{1}^{2} + {{b}_{2}}J_{1}^{3}{{J}_{2}} + J_{2}^{2} + J_{1}^{4} \\ \end{gathered} $ | 7 |
| 5 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2} + {{a}_{4}}{{J}_{1}}{{J}_{2}} + \\ + \,\,{{a}_{5}}J_{1}^{3} + J_{2}^{2} + {{b}_{1}}J_{1}^{4} + {{b}_{2}}J_{1}^{5} \\ \end{gathered} $ | 8 |
Таблица 2.
Феноменологические модели с L = C4v
| c | F | μ |
|---|---|---|
| 1 | ${{a}_{1}}{{J}_{1}} + J_{1}^{2} + {{b}_{1}}{{J}_{2}}$ | 3 |
| 2 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + J_{1}^{2} + {{b}_{1}}J_{2}^{2}$ | 4 |
| 3 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2} + {{b}_{1}}{{J}_{1}}{{J}_{2}} + J_{1}^{3} + {{b}_{2}}J_{2}^{2} + J_{1}^{4}$ | 6 |
| 4 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2} + {{a}_{4}}{{J}_{1}}{{J}_{2}} + \\ + \,\,J_{1}^{3} + {{b}_{1}}J_{2}^{2} + {{b}_{2}}{{J}_{1}}J_{2}^{2} \\ \end{gathered} $ | 7 |
| 5 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2} + {{a}_{4}}{{J}_{1}}{{J}_{2}} + {{a}_{5}}J_{1}^{3} + \\ + \,\,J_{2}^{2} + J_{1}^{4} + {{b}_{1}}J_{1}^{2}{{J}_{2}} + {{b}_{2}}J_{1}^{5} + {{b}_{3}}J_{1}^{6} + {{b}_{4}}J_{2}^{3} \\ \end{gathered} $ | 10 |
Таблица 3.
Феноменологические модели с L = C6v
| c | F | μ |
|---|---|---|
| 1 | ${{a}_{1}}{{J}_{1}} + J_{1}^{2} + {{b}_{1}}{{J}_{2}}$ | 3 |
| 2 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}J_{1}^{2} + J_{1}^{3} + {{J}_{2}} + {{b}_{1}}{{J}_{1}}{{J}_{2}}$ | 4 |
| 3 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}J_{1}^{2} + {{a}_{3}}J_{1}^{3} + {{J}_{2}} + {{b}_{1}}J_{1}^{4}$ | 5 |
| 4 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}J_{1}^{2} + {{a}_{3}}J_{1}^{3} + {{a}_{4}}{{J}_{2}} + \\ + \,\,J_{1}^{4} + {{J}_{1}}{{J}_{2}} + {{b}_{1}}J_{1}^{5} + {{b}_{2}}J_{1}^{6} \\ \end{gathered} $ | 7 |
| 5 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}J_{1}^{2} + {{a}_{3}}J_{1}^{3} + {{a}_{4}}{{J}_{2}} + \\ + \,\,{{a}_{5}}J_{1}^{4} + {{J}_{1}}{{J}_{2}} + {{b}_{1}}J_{1}^{5} + {{b}_{2}}J_{2}^{2} \\ \end{gathered} $ | 8 |
В табл. 1–3 в первом столбце указано число управляющих параметров моделей, во втором – феноменологические модели F, соотвествующие данному числу управляющих параметров, записанные в безразмерной математической форме, в третьем указана кратность μ вырожденной критической точки, которой является точка фазового перехода. Кратность указывает максимальное число особых точек [8] на фазовых диаграммах моделей, на которые распадается вырожденная критическая точка при изменении управляющих параметров.
Некоторые модели, представленные в таблицах, внешне совпадают с моделями, построенными традиционным методом простого разложения в ряд Тейлора [9, 10]. Однако есть два существенных отличия. Во-первых, в теории катастроф разложение проводится в формальный, то есть, не обязательно сходящийся ряд Тейлора и не требующий малости параметра порядка. Во-вторых, не все феноменологические коэффициенты в термодинамическом потенциале зависят от параметров, варьируемых в эксперименте. В ряде работ последних лет [11–13] методы эквивариантной теории катастроф успешно применяются для построения феноменологических моделей фазовых переходов.
Фазовые диаграммы моделей с одним управляющим параметром одномерны и содержат одну вырожденную критическую точку фазового перехода из высокосимметричной фазы (00) в низкосимметричную (η0) или (ηη). Перенормировкой параметра порядка и феноменологических коэффициентов можно показать [14], что феноменологические модели в этом случае сводятся к потенциалу Ландау для одного однокомпонентного параметра порядка. У моделей с двумя управляющими параметрами двумерные фазовые диаграммы. Примечательно, что эти модели для L = C3v и L = C4v не только имеют одинаковый вид в пространстве базисных инвариантов
(различие только в инвариантах J2), но и сходную топологию фазовых диаграмм. Потенциалы (11) описывают все возможные фазы, присущие моделям с данной симметрией параметра порядка. Для L = C3v это фазы I. (00), II. (η0), III. (–η0), IV. (η1η2) (рис. 1а), модель с L = C4v описывает фазы I. (00), II. (η0), III. (ηη), IV. (η1η2) (рис. 1б). Отрезки парабол в верхней полуплоскости являются границами фазовых переходов 1-го рода, полукубические параболы в полуплоскости a1 < 0 – границы фазовых переходов 2-го рода в низкосимметричную фазу (η1η2). Точка 0 (начало координат) на фазовой диаграмме – тетракритическая точка, в которой сходятся границы всех четырех фаз, то есть кратность этой точки равна μ = 4 (см. табл. 1 и 2).
Рис. 1.
Фазовые диаграммы моделей с L = C3v (а) и L = C4v (б). Сплошные линии – границы фазовых переходов первого рода, штриховые – границы фазовых переходов второго рода, штрихпунктирные линии – границы равновесия фаз.

Целый рациональный базис инвариантов (ЦРБИ) для групп L = Cn (n = 3, 4, 6, …) двухкомпонентного параметра порядка содержит три инварианта
Результат классификации термодинамических потенциалов с симметрией параметра порядка, описываемой группами L = C3 и L = C4 приведен в табл. 4 и 5. Обозначения те же, что и в табл. 1–3, причем ${{J}_{1}} = {{r}^{2}},$ ${{J}_{2}} = {{r}^{n}}\cos n\varphi ,$ ${{J}_{3}} = {{r}^{n}}\sin n\varphi ,$ η1 = = r cos φ, η2 = r sin φ (n = 3, 4).
Таблица 4.
Феноменологические модели с L = C3
| c | F | μ |
|---|---|---|
| 1 | Нет модели | |
| 2 | Нет модели | |
| 3 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}{{J}_{3}} + J_{1}^{2} + {{b}_{1}}J_{2}^{2}$ | 5 |
| 4 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}{{J}_{3}} + \\ + \,\,{{a}_{4}}J_{1}^{2} + {{J}_{1}}{{J}_{2}} + {{b}_{1}}{{J}_{1}}{{J}_{3}} + {{b}_{2}}J_{1}^{3} \\ \end{gathered} $ | 6 |
| 5 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}{{J}_{3}} + {{a}_{4}}J_{1}^{2} + \\ + \,\,{{a}_{5}}{{J}_{1}}{{J}_{2}} + {{J}_{1}}{{J}_{3}} + {{b}_{1}}J_{2}^{2} + {{b}_{2}}J_{1}^{3} \\ \end{gathered} $ | 8 |
| 6 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}{{J}_{3}} + {{a}_{4}}J_{1}^{2} + {{a}_{5}}{{J}_{1}}{{J}_{2}} + \\ + \,\,{{a}_{6}}{{J}_{1}}{{J}_{3}} + J_{1}^{3} + {{b}_{1}}J_{2}^{2} + {{b}_{2}}{{J}_{2}}{{J}_{3}} + {{b}_{3}}J_{1}^{4} \\ \end{gathered} $ | 10 |
Таблица 5.
Феноменологические модели с L = C4
| c | F | μ |
|---|---|---|
| 1 | ${{a}_{1}}{{J}_{1}} + J_{1}^{2} + {{b}_{1}}{{J}_{3}}$ | 3 |
| 2 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + J_{1}^{2} + {{b}_{1}}{{J}_{3}}$ | 4 |
| 3 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}{{J}_{3}} + J_{1}^{2} + {{b}_{1}}J_{2}^{2}$ | 5 |
| 4 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}{{J}_{3}} + {{a}_{4}}J_{1}^{2} + J_{1}^{3} + {{b}_{1}}{{J}_{1}}{{J}_{2}} + \\ + \,\,{{b}_{2}}{{J}_{1}}{{J}_{3}} + J_{1}^{4} + {{b}_{3}}J_{2}^{2} + {{b}_{4}}J_{3}^{2} + {{b}_{5}}{{J}_{1}}J_{2}^{2} \\ \end{gathered} $ | 10 |
Анализ моделей, приведенных в таблицах, показывает, что термодинамический потенциал с одним управляющим параметром заменой переменных и перенормировкой феноменологических коэффициентов сводится к потенциалу Ландау 4-й степени [1] и описывает только один фазовый переход второго рода в точке а1 = 0. На фазовой диаграмме модели с двумя управляющими параметрами присутствует только трикритическая точка, разделяющая линии фазовых переходов первого и второго рода. Для описания последовательнсти структурных фазовых переходов нужно использовать, по крайней мере, модель с тремя управляющими параметрами. Такая модель с L = C4 применена в работе [15] для описания фазовых переходов в вольфрамате рубидия–диспрозия RbDy(WO4)2.
В размерной физической форме термодинамический потенциал имеет вид
(12)
$\begin{gathered} \Phi = {{\Phi }_{0}} + \frac{1}{2}{{a}_{1}}{{r}^{2}} + \frac{1}{4}{{a}_{2}}{{r}^{4}}\cos 4\varphi + \\ + \,\,\frac{1}{4}{{a}_{3}}{{r}^{4}}\sin 4\varphi + \frac{1}{4}{{b}_{1}}{{r}^{4}} + \frac{1}{8}{{b}_{2}}{{r}^{8}}{{\cos }^{2}}4\varphi . \\ \end{gathered} $Здесь Ф0 – часть термодинамического потенциала, не зависящая от параметра порядка, a1 – a3 – феноменологические коэффициенты, являющиеся управляющими параметрами, причем ${{a}_{1}} = a_{1}^{'}(T - {{T}_{c}}),$ Тс = 9 К, коэффициенты b1 > 0 и b2 > 0.
Учет в модели только членов четвертой степени приводит к структурно неустойчивым результатам, в частности, к появлению на фазовой диаграмме безгистерезисного фазового перехода первого рода [16]. Добавление в (12) членов шестой степени не меняет топологию фазовой диаграммы.
Модель (12) описывает две устойчивые фазы: высокосимметричную с r = 0, φ = 0 (η1 = η2 = 0) и низкосимметричную с r ≠ 0, φ ≠ 0 (η1 ≠ η2 ≠ 0).
Фазовая диаграмма модели приведена на рис. 2. Область высокосимметричной фазы (00) при a1 > 0 отделена от области низкосимметричной фазы (r φ) границами фазовых переходов первого и второго рода. На плоскости a1 = 0 окружность $a_{2}^{2} + a_{3}^{2} = b_{1}^{2}$ представляет собой геометрическое место трикритических точек, разделяющих области фазового перехода второго рода при $a_{2}^{2} + a_{3}^{2} < b_{1}^{2}$ и фазового перехода первого рода при $a_{2}^{2} + a_{3}^{2} > b_{1}^{2}.$ Низкосимметричная фаза реализуется в нижнем полупространстве (a1 < 0), при этом в конусе, имеющем в основании астроиду, сосуществуют две изоморфные фазы. Изоморфный фазовый переход первого рода происходит на поверхности, соединяющей противоположные ребра конуса, которые являются линиями критических точек типа жидкость–пар. Уравнение, определяющее бифуркационную поверхность изоморфных фазовых переходов, можно записать в параметрическом виде:
Двумерное сечение фазовой диаграммы в координатах a1–a2 (a3 = const) изображено на рис. 3. Штрих-пунктирная линия a1 = 0 при $a_{2}^{2} < b_{1}^{2} - a_{3}^{2}$ определяет границу фазового перехода второго рода, отрезки парабол – границы фазового перехода первого рода. Прямая а1 = 0 при $a_{2}^{2} > b_{1}^{2} - a_{3}^{2}$ и отрезки полукубической параболы $4{{\left( {{{a}_{2}} + 1} \right)}^{3}} + 27{{b}_{2}}a_{1}^{2} = 0$ – границы равновесия фаз. Полукубическая парабола с концевой точкой А типа жидкость–пар является линией изоморфных фазовых переходов. Поскольку в модели (12) от температуры зависит только один коэффициент ${{a}_{1}} = a_{1}^{'}(T - {{T}_{c}}),$ термодинамический путь αα' на фазовой диаграмме является прямой, параллельной оси a1 (рис. 3). Если при этом он проходит на расстоянии от оси, удовлетворяющем условию $a_{2}^{2} < b_{1}^{2} - a_{3}^{2},$ то пересекает линию фазовых переходов второго рода и линию изоморфных фазовых переходов. Таким образом, на температурных зависимостях физических свойств существуют две аномалии, соответствующие фазовым переходам второго и первого рода при понижении температуры. Причем фазовый переход первого рода в данной модели является изоморфным, то есть при этом переходе не меняется пространственная симметрия кристалла.
Рис. 3.
Двумерное сечение фазовой диаграммы модели (12). Обозначения те же, что и на рис. 1, А – концевая критическая точка типа жидкость–пар.

На основе модели (12) рассчитана теоретическая кривая теплоемкости и сопоставлена с экспериментальными результатами в RbDy(WO4)2 (рис. 4).
Рис. 4.
Температурные зависимости теплоемкости в ${\text{RbDy}}{{\left( {{\text{W}}{{{\text{O}}}_{{\text{4}}}}} \right)}_{{\text{2}}}}.$ Крестики – экспериментальные данные работы [17], кружки – теоретические значения, рассчитанные по модели (12).

Теоретические значения, обозначены на рис. 4 кружками, крестики – экспериментальные результаты работы [17]. Как видно, сопоставление теоретических и экспериментальных данных показывает удовлетворительное качественное соответствие.
ФЕНОМЕНОЛОГИЧЕСКИЕ МОДЕЛИ С ТРЕХКОМПОНЕНТНЫМ ПАРАМЕТРОМ ПОРЯДКА
Базисные инварианты трехкомпонентных параметров порядка определяются по симметрии L‑групп, изоморфных точечным группам тетраэдра и куба. Здесь приведены результаты классификации моделей с параметрами порядка для двух групп: L = Td и L = Oh.
В случае L = Td ЦРБИ представим в виде:
(13)
$\begin{gathered} {{J}_{1}} = {\eta }_{1}^{2} + {\eta }_{2}^{2} + {\eta }_{3}^{2},\,\,\,\,{{J}_{2}} = {{{\eta }}_{1}}{{{\eta }}_{2}}{{{\eta }}_{3}}, \\ {{J}_{3}} = {\eta }_{1}^{2}{\eta }_{2}^{2} + {\eta }_{2}^{2}{\eta }_{3}^{2} + {\eta }_{1}^{2}{\eta }_{3}^{2}. \\ \end{gathered} $Здесь J1, J2, J3, – базисные инварианты, η1, η2, η3 – компоненты параметра порядка.
Разложим термодинамический потенциал в ряд по степеням базисных инвариантов и выделим слагаемые, однородные по степеням параметра порядка:
(14)
$\begin{gathered} F = \underbrace {{{a}_{1}}{{J}_{1}}}_2 + \underbrace {{{a}_{2}}{{J}_{2}}}_3 + \underbrace {{{a}_{3}}{{J}_{3}} + {{a}_{4}}J_{1}^{2}}_4 + \\ + \,\,\underbrace {{{a}_{5}}{{J}_{1}}{{J}_{2}}}_5 + \underbrace {{{a}_{6}}J_{1}^{3} + {{a}_{7}}J_{2}^{2} + {{a}_{8}}{{J}_{1}}{{J}_{3}}}_6 + .... \\ \end{gathered} $Под фигурными скобками указаны степени слагаемых по компонентам параметра порядка.
Пусть число управляющих параметров с = 2. Тогда подбором параметров, варьируемых в эксперименте, можно положить a1 = a2 = 0. Из (14) следует, что однородная часть наименьшей четвертой степени ${{f}_{0}} = {{a}_{4}}J_{1}^{2} + {{J}_{3}}.$ Так как потенциал задается в безразмерной математической форме, можно положить a3 = 1.
Эквивариантные векторные поля в пространстве базисных инвариантов определяются подстановкой инвариантов (13) в формулу (5):
(15)
$\begin{gathered} {{U}_{1}} = 2{{J}_{1}}\frac{\partial }{{\partial {{J}_{1}}}} + 3{{J}_{2}}\frac{\partial }{{\partial {{J}_{2}}}} + 4{{J}_{3}}\frac{\partial }{{\partial {{J}_{3}}}}, \\ {{U}_{2}} = 3{{J}_{2}}\frac{\partial }{{\partial {{J}_{1}}}} + 2{{J}_{3}}\frac{\partial }{{\partial {{J}_{2}}}} + 2{{J}_{1}}{{J}_{2}}\frac{\partial }{{\partial {{J}_{3}}}}, \\ {{U}_{3}} = 4{{J}_{3}}\frac{\partial }{{\partial {{J}_{1}}}} + 2{{J}_{1}}{{J}_{2}}\frac{\partial }{{\partial {{J}_{2}}}} + \left( {3J_{2}^{2} + 4{{J}_{1}}{{J}_{3}}} \right)\frac{\partial }{{\partial {{J}_{3}}}}. \\ \end{gathered} $Подействуем на f0 эквивариантными векторными полями (15):
(16)
$\begin{gathered} {{U}_{1}}{{f}_{0}} = 4{{a}_{4}}J_{1}^{2} + 4{{J}_{3}} \in {{I}_{{\nabla {{f}_{0}}}}}, \\ {{U}_{2}}{{f}_{0}} = 2\left( {3{{a}_{4}} + 1} \right){{J}_{1}}{{J}_{2}} \in {{I}_{{\nabla {{f}_{0}}}}}, \\ {{U}_{3}}{{f}_{0}} = 4{{J}_{1}}{{J}_{3}}\left( {2{{a}_{4}} + 1} \right) + 3J_{2}^{2} \in {{I}_{{\nabla {{f}_{0}}}}}. \\ \end{gathered} $Из (16) следует, что моном J1J2 лежит в идеале ${{I}_{{\nabla {{f}_{0}}}}},$ а мономы $J_{1}^{2}$ и J3, а также J1J3 и $J_{2}^{2}$ сравнимы по идеалу. Используя то обстоятельство, что если Ukf0 лежит в идеале, то и $J_{p}^{n}$Ukf0 также принадлежит идеалу, умножим U3f0 на J2 и убедимся, что $J_{2}^{3}$ также лежит в идеале, поскольку моном J1J2 – один из образующих идеала:
Аналогично находятся остальные мономы, являющиеся образующими идеала. В итоге получаем конечную факторалгебру из мономов, составляющих слагаемые модели с двумя управляющими параметрами:
(17)
$F = {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{J}_{3}} + {{b}_{1}}J_{1}^{2} + {{b}_{2}}J_{1}^{3} + {{b}_{3}}J_{2}^{2}.$В модели (17) появились слагаемые степени выше четвертой. Коэффициенты при этих слагаемых bi являются модулями и определяют бифуркационный тип фазовой диаграммы, а вместе с управляющими параметрами и кратность вырожденной критической точки.
Подобным образом строятся модели с другим числом управляющих параметров. Эти модели для L = Td ($\bar {4}$3m) представлены в классификационной табл. 6. Обозначения те же, что и в предыдущих таблицах. Коэффициенты ai в табл. 6 – управляющие параметры, bi – модули.
Таблица 6.
Феноменологические модели с L = Td ($\bar {4}$3m)
| c | F | μ |
|---|---|---|
| 1 | ${{a}_{1}}{{J}_{1}} + {{J}_{2}} + {{b}_{1}}J_{1}^{2}$ | 3 |
| 2 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{J}_{3}} + {{b}_{1}}J_{1}^{2} + {{b}_{2}}J_{1}^{3} + {{b}_{3}}J_{2}^{2}$ | 6 |
| 3 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}{{J}_{3}} + J_{1}^{2} + {{b}_{1}}J_{2}^{2} + {{b}_{2}}J_{3}^{2} + {{b}_{3}}{{J}_{2}}{{J}_{3}}$ | 7 |
| 4 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2} + {{a}_{4}}{{J}_{3}} + {{J}_{1}}{{J}_{2}} + \\ + \,\,{{b}_{1}}J_{1}^{3} + {{b}_{2}}J_{1}^{4} + {{b}_{3}}J_{1}^{5} + {{b}_{4}}J_{2}^{2} + {{b}_{5}}J_{3}^{2} \\ \end{gathered} $ | 10 |
Все возможные симметрийно неэквивалентные фазы, описываемые термодинамическими потенциалами с группой симметрии параметра порядка L = Td ($\bar {4}$3m), следующие [18]: фаза 1 высокосимметричная, η1 = η2 = η3 = 0; фаза 2, η1 = = η2 = η3 ≠ 0 (в ней сосуществуют две антиизоструктурные фазы: 2A (η, η, η); η > 0 и 2B (−η, η, η); η > 0); фаза 3, η1 ≠ 0, η2 = η3 = 0; фаза 4, η1 = η2 ≠ η3, в которой сосуществуют также две антиизоструктурные фазы: 4A (η1, η1, η3); η1 > 0, η3 > 0 и 4B (−η1, η1, η3); η1 > 0, η3 > 0; фаза 5, η1 ≠ η2 ≠ η3 ≠ 0 – наиболее низкосимметричная (трехпараметрическая) фаза.
Анализ фазовых диаграмм моделей, приведенных в классификационной табл. 6, показал, что модель с одним управляющим параметром описывает один фазовый переход из фазы 1 в фазу 2. Заменой параметра порядка и перенормировкой феноменологических коэффициентов эта модель сводится к катастрофе типа сборка [4]. В модели с двумя управляющими параметрами (c = 2) реализуются кроме высокосимметричной фазы 1 также фазы 2, 3 и 4. Модель с тремя управляющими параметрами в размерной физической форме
(18)
$\begin{gathered} \Phi = {{{\alpha }}_{1}}{{J}_{1}} + {{{\alpha }}_{2}}J_{1}^{2} + {{{\beta }}_{1}}{{J}_{2}} + {{{\beta }}_{2}}J_{2}^{2} + \\ + \,\,{{{\gamma }}_{1}}{{J}_{3}} + {{{\gamma }}_{2}}J_{3}^{2} + {{{\delta }}_{{23}}}{{J}_{2}}{{J}_{3}}, \\ \end{gathered} $Типичные двумерные сечения фазовой диаграммы модели (18) в координатах β1–α1 для различных значений этих коэффициентов представлены на рис. 5.
Рис. 5.
Типичные сечения фазовой диаграммы модели (18) в координатах β1–α1 при различных значениях феноменологических коэффициентов: а – α2 = β2 = γ1 = γ2 = δ23= 1; б – α2 = β2 = γ2 = 1 γ1 = δ23= –1.

В рамках модели (18) рассчитана теоретическая зависимость аномальной части теплоемкости и сопоставлена с экспериментальными данными теплоемкости в GaV4S8 [19, 20]. Это соединение имеет кубическую структуру с пространственной группой симметрии F$\bar {4}$3m и при низких температурах испытывает два последовательных фазовых перехода – в ромбоэдрическую фазу с симметрией R3m (фаза 2) при ТС1 = 44 К, затем в орторомбическую фазу 3 с симметрией Imm2 (ТС2 = 13 К). Между группами R3m и Imm2 нет соотношения группа–подгруппа, однако они обе являются подгруппами исходной высокотемпературной фазы и именно в таком порядке располагаются на двумерном сечении фазовой диаграммы модели (18) для термодинамического пути аа' (см. рис. 5а).
Температурная зависимость аномальной части теплоемкости приведена на рис. 6. Крестиками на рисунке обозначены экспериментальные результаты аномальной части теплоемкости в GaV4S8, вычисленные по данным работы [19]. Как видно на рис. 6, теоретическая кривая теплоемкости качественно удовлетворительно описывает данные эксперимента. Заметим, что аналогичные аномалии физических свойств наблюдаются также в твердых растворах GaxGe1 –xV4S8 [20].
Рис. 6.
Температурные зависимости аномальной части теплоемкости в GaV4S8. Крестики – экспериментальные данные работы [19], кривая – теоретическая зависимость, рассчитанная по модели (18).

Рассмотрим феноменологическую модель с трехкомпонентным параметром порядка (η1,η2,η3), симметрией параметра порядка L = Oh и с числом управляющих параметров с = 2. В этом случае ЦРБИ состоит из трех инвариантов:
(19)
$\begin{gathered} {{J}_{1}} = {\eta }_{1}^{2} + {\eta }_{2}^{2} + {\eta }_{3}^{2},\,\,\,\,{{J}_{2}} = {\eta }_{1}^{4} + {\eta }_{2}^{4} + {\eta }_{1}^{4}, \\ {{J}_{3}} = {\eta }_{1}^{2}{\eta }_{2}^{2}{\eta }_{3}^{2}. \\ \end{gathered} $Разложим термодинамический потенциал в ряд по степеням базисных инвариантов и выделим слагаемые, однородные по степеням параметра порядка. Тогда:
(20)
$F = \underbrace {{{a}_{1}}{{J}_{1}}}_2 + \underbrace {{{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2}}_4 + \underbrace {{{a}_{4}}{{J}_{3}} + {{a}_{5}}J_{1}^{3} + {{a}_{6}}{{J}_{1}}{{J}_{2}}}_6 + ....$Под фигурными скобками указаны степени слагаемых по компонентам параметра порядка.
Поскольку с = 2, то подбором параметров, варьируемых в эксперименте, можно положить a1 = = a2 = 0. Тогда из (20) следует, что однородная часть наименьшей четвертой степени ${{f}_{0}} = {{a}_{3}}J_{1}^{2}.$ Так как потенциал задается в безразмерной математической форме, можно положить a3 = 1.
Эквивариантные векторные поля в пространстве базисных инвариантов определяются подстановкой инвариантов (19) в формулу (5)
(21)
$\begin{gathered} {{U}_{1}} = {{J}_{1}}\frac{\partial }{{\partial {{J}_{1}}}} + 2{{J}_{2}}\frac{\partial }{{\partial {{J}_{2}}}} + 3{{J}_{3}}\frac{\partial }{{\partial {{J}_{3}}}}, \\ {{U}_{2}} = 2{{J}_{2}}\frac{\partial }{{\partial {{J}_{1}}}} + \left( {{{J}_{1}}{{J}_{2}} + 3{{J}_{3}}} \right)\frac{\partial }{{\partial {{J}_{2}}}} + 2{{J}_{1}}{{J}_{3}}\frac{\partial }{{\partial {{J}_{3}}}}, \\ {{U}_{3}} = 3{{J}_{3}}\frac{\partial }{{\partial {{J}_{1}}}} + 2{{J}_{1}}{{J}_{3}}\frac{\partial }{{\partial {{J}_{2}}}} + {{J}_{2}}{{J}_{3}}\frac{\partial }{{\partial {{J}_{3}}}}. \\ \end{gathered} $Действуя на f0 эквивариантными векторными полями (21), можно найти мономы, являющиеся образующими идеала по схеме, описанной ранее. Конечная факторалгебра из мономов, составляющих слагаемые модели с двумя управляющими параметрами, имеет вид:
(22)
$\begin{gathered} F = {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + J_{1}^{2} + {{b}_{1}}J_{2}^{2} + \\ + \,\,{{b}_{2}}{{J}_{3}} + {{b}_{3}}J_{1}^{3} + {{b}_{4}}{{J}_{2}}{{J}_{3}}. \\ \end{gathered} $Коэффициенты bi, как и раньше, являются модулями. Подобным образом строятся модели с другим числом управляющих параметров. Эти модели для L = Oh (m$\bar {3}$m) представлены в классификационной табл. 7.
Таблица 7.
Феноменологические модели с L = Oh (m$\bar {3}$m)
| c | F | μ |
|---|---|---|
| 1 | ${{a}_{1}}{{J}_{1}} + J_{1}^{2} + {{b}_{1}}{{J}_{2}} + {{b}_{2}}{{J}_{3}} + {{b}_{3}}J_{1}^{3}$ | 5 |
| 2 | ${{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + J_{1}^{2} + {{b}_{1}}J_{2}^{2} + {{b}_{2}}{{J}_{3}} + {{b}_{3}}J_{1}^{3} + {{b}_{4}}{{J}_{2}}{{J}_{3}}$ | 7 |
| 3 | $\begin{gathered} {{a}_{1}}{{J}_{1}} + {{a}_{2}}{{J}_{2}} + {{a}_{3}}J_{1}^{2} + J_{1}^{3} + {{b}_{1}}{{J}_{3}} + {{b}_{2}}{{J}_{1}}{{J}_{2}} + \\ + \,\,{{b}_{3}}J_{1}^{4} + {{b}_{4}}{{J}_{1}}{{J}_{3}} + {{b}_{5}}J_{1}^{5} + {{b}_{6}}{{J}_{2}}{{J}_{3}} + {{b}_{7}}J_{1}^{6} + \\ + \,\,{{b}_{8}}J_{1}^{4}{{J}_{2}} + {{b}_{9}}J_{2}^{3} + {{b}_{{10}}}J_{3}^{2} \\ \end{gathered} $ | 14 |
Анализ фазовых диаграмм показывает, что модель с двумя управляющими параметрами описывает все возможные фазы, реализуемые в монокристаллах и пьезокерамике со структурой типа перовскита.
Как показывает теоретико-групповой анализ, существует 7 возможных фаз, описываемых термодинамическими потенциалами с группой симметрии параметра порядка L = Oh (m$\bar {3}$m), которые имеют следующий вид [21]: кубическая Pm$\bar {3}$m (С) η1 = η2 = η3 = 0; тетрагональная P4mm (Т) η1 ≠ 0, η2 = η3 = 0; орторомбическая Amm2 (O) η1 = η2 ≠ 0, η3 = 0; ромбоэдрическая R3m (R) η1 = η2 = η3 ≠ 0; моноклинная Cm (M1) η1 = η2 ≠ η3; моноклинная Pm (M2) η1 ≠ η2 ≠ 0, η3 = 0; триклинная P1 (Tr) η1 ≠ ≠ η2 ≠ η3 ≠ 0.
Исследование фазовых диаграмм термодинамических потенциалов из классификационной табл. 7, проведенное методом компьютерного моделирования, показало, что модель с одним управляющим параметром описывает один фазовый переход из высокосимметричной кубической фазы в одну из низкосимметричных, в зависимости от соотношения феноменологических коэффициентов. В модели с двумя управляющими параметрами (c = 2) реализуются все низкосимметричные фазы.
Сечение фазовой диаграммы модели (22) в координатах β1–α1 представлено на рис. 7. Из рисунка видно, что фазовая диаграмма модели с двумя управляющими параметрами, построенная методами теории катастроф, содержит все возможные фазы перовскитоподобных кристаллов.
Фазовые диаграммы модели, построенные методами теории катастроф, при различных значениях феноменологических коэффициентов и экспериментальные фазовые диаграммы х–Т твердых растворов цинкониобата, легированных титанатом свинца, (1 − x)Pb(Zn1/3Nb2/3)O3−xPbTiO3 (PZN-PT) и магнониобата свинца–титаната свинца Pb(Mg1/3Nb2/3)O3–PbTiO3 (PMN-PT) приведены на рис. 8 и 9. Как видно из рисунков, экспериментальные и теоретические фазовые диаграммы топологически эквивалентны.
Рис. 8.
Экспериментальная х–Т фазовая диаграмма твердого раствора цинкониобата свинца, легированного титанатом свинца [22], (а) и теоретическая фазовая диаграмма (б), построенная по модели (22).

Рис. 9.
Экспериментальная х–Т фазовая диаграмма магнониобата свинца–титаната свинца [23] (а) и теоретическая фазовая диаграмма (б), построенная по модели (22).

ЗАКЛЮЧЕНИЕ
Теория катастроф с применением эквивариантных векторных полей позволяет строить феноменологические модели фазовых переходов для многокомпонентных и взаимодействующих параметров порядка, причем эти модели структурно устойчивы и имеют более компактный вид по сравнению с моделями, построенными традиционным методом. Классификация моделей по числу управляющих параметров выявляет все возможные виды термодинамических потенциалов для данной симметрии параметров порядка. Исследование фазовых диаграмм моделей позволяет проследить эволюцию появления и топологию низкосимметричных фаз в зависимости от числа управляющих параметров, варьируемых в эксперименте, а также провести сопоставление с имеющимися экспериментальными данными.
Список литературы
Ландау Л.Д. К теории фазовых переходов. Собр. трудов. Т. 1. М.: Наука, 1967. 510 с.
Кутьин Е.И., Лорман В.Л., Павлов С.В. // УФН. 1991. Т. 161. № 6. С. 109; Kut’in E.I., Lorman V.L., Pavlov S.V. // Sov. Phys. – Uspekhi. 1991. V. 34. № 10. P. 497.
Павлов С.В. // Методы теории катастроф в исследованиях фазовых переходов. М.: Изд-во Моск. ун-та, 1993. 104 с.
Постон Т., Стюарт И. // Теория катастроф и ее применения. М.: Мир, 1980. 607 с.
Широков В.Б. // Вестник Южного науч. центра. 2012. Т. 8. № 2. С. 3.
Арнольд В.И., Варченко А.Н., Гусейн-Заде С.М. // Особенности дифференцируемых отображений. Т. 1. Классификация критических точек, каустик и волновых фронтов. М.: Наука, 1982. 304 с.
Гуфан Ю.М. // Структурные фазовые переходы. М.: Наука, 1982. 304 с.
Гуфан Ю.М., Ларин Е.С. // Изв. АН СССР. Сер. физ. 1979. Т. 43. № 8. С. 1567.
Гуфан Ю.М., Сахненко В.П. // ЖЭТФ. 1972. Т. 63. № 5. С. 1909; Gufan Yu.M., Sakhnenko V.P. // Sov. Phys. JETF. V. 36. № 5. 1973. P. 1009.
Муковнин А.А., Таланов В.М. // Журн. физ. химии. 2012. Т. 86. № 12. С. 1920; Mukovnin A.A., Talanov V.M. // Rus. J. Phys. Chem. A. 2012. V. 86. № 12. P. 1785.
Шамшин А.П., Изотова Т.М., Матюшкин Э.В. и др. // Изв. РАН. Сер. физ. 2004. Т. 68. № 7. С. 945; Shamshin A.P., Izotova T.M., Matyushkin E.V. et al. // Bull. Russ. Acad. Sci. Phys. 2004. V. 68. № 7. P. 1061.
Таланов В.М., Широков В.Б., Торгашев В.И. и др. // Физ. и хим. стекла. 2007. Т. 34. С. 822.
Kim I., Jang K., Li L. // Phase Transitions. 2018. V. 91. № 3. P. 239.
Павлов С.В. // Вестн. Моск. ун-та. Сер. 3. Физ. Астрон. 2016. № 2 С. 62; Pavlov S.V. // Moscow Univer. Phys. Bull. 2016. № 2. P. 202.
Павлов С.В. // Вестн. Моск. ун-та. Сер. 3. Физ. Астрон. 2017. № 6. С. 74; Pavlov S.V. // Moscow Univer. Phys. Bull. 2017. V. 72. № 6. P. 569.
Galam S., Hatch D.M. // Phys. Rev. B. 1986. V. 34. № 11. P. 7813.
Дьяконов В.П., Маркович В.И., Коварский А.В. и др. // ФТТ. 1998. Т. 40. № 12. С. 2221; D’yakonov V.P., Markovich V.I., Kovarskii V.L. et al. // Phys. Sol. St. 1998. V. 40. № 12. P. 2017.
Mukovnin A.A., Talanov V.M. // Sol. St. Comm. 2014. V. 182. № 1. P. 1.
Ruff E., Widmann S., Lunkenheimer P. et al. // Sci. Adv. 2015. V. 1. № 10. Art. № e1500916
Bichler D., Slavik H., Johrendt D. // Zeitschrift fur Naturforschung B. 2009. V. 64. № 8. P. 915.
Sergienko I.A., Gufan Yu.M., Urazhdin S. // Phys. Rev. B. 2002. V. 65. № 14. Art. № 144104.
La-Orauttapong D., Noheda B., Ye Z.-G. et al. // Phys. Rev. B. 2002. V. 65. № 14. Art. № 144101.
Ye Z.-G., Noheda B., Dong M. et al. // Phys. Rev. B. 2001. V. 64. № 18. Art. № 184114.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая




