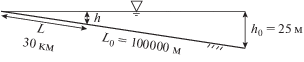Известия РАН. Серия физическая, 2020, T. 84, № 1, стр. 101-105

ВВЕДЕНИЕ

На поверхности потоков воды возникают стационарные волны с неподвижными гребнями, если скорость течения меняется в направлении движения $\left( {{{u}_{x}} = \frac{{\partial u}}{{\partial x}} \ne 0} \right)$ и превышает значение u > > 23.1 см ∙ с^–1 [1]. Длина стационарной волны $\lambda $ определяется числом Фруда, если оно удовлетворяет условию $Fr = {u \mathord{\left/ {\vphantom {u {\sqrt {gh} < 1}}} \right. \kern-0em} {\sqrt {gh} < 1}},$ (g – ускорение силы тяжести, h – глубина слоя воды). Крутизна волны $ak = a\frac{{2\pi }}{\lambda },$ где a – амплитуда волны, растет при увеличении продольного градиента скорости течения ${{u}_{x}}.$ Нелинейные стационарные волны большой крутизны $ak > 0.2$ на поверхности потока в канале конечной ширины впервые исследованы нами экспериментально в [2]. В работе установлено, что в зоне торможения течения ${{u}_{x}} < 0$ под передним склоном волны в вязком слое потока у дна канала происходит интенсивный отрыв цилиндрических вихрей. Вихри захватывают и уносят частицы грунта, формируя промоину под передним склоном волны. Под задним склоном волны, где ${{u}_{x}} > 0,$ вихри не образуются, там происходит накопление грунта и в результате формируется гребень гряды. Расстоянием между грядами равно длине стационарной волны. При увеличении значений ${{u}_{x}}$ потока крутизна стационарной волны растет, а при достижении критического значения $0.31 < {{\left( {ak} \right)}_{{cr}}} < 0.37$ происходит распад плоской волны на две трехмерные волны большей длины, имеющие поперечную модуляцию фронта [3]. Новые волны имеют ту же фазовую скорость, что и исходная волна по условию фазового синхронизма взаимодействия нелинейных волн. В результате новые стационарные трехмерные волны формируют на дне трехмерные гряды. Гребни гряд, как и гребни волн, расположены в шахматном порядке. Длины трехмерных волн, возникших после распада плоской волны, близки при числах Фруда Fr < 0.66. При увеличении чисел Фруда отношение длин трехмерных волн быстро растет, в диапазоне $0.68 < Fr < 0.73$ длины волн отличаются друг от друга на 1–2 порядка, причем амплитуда самой длинной волны максимальна. Эта волна формирует гряду максимальной высоты при пиковых расходах воды. После спада паводка вершины гряды возвышаются над поверхностью воды и не деформируется. По форме гряды максимальной длины и высоты можно оценить параметры пикового расхода воды [4]. Особую ценность эти оценки имеют для неконтролируемых потоков воды, возникающих, например, при прорыве искусственных или естественных плотин. Другим примером является резкие колебания уровня моря при тектонических сдвигах. Известно, что уровень воды в Каспийском море испытывал значительные колебания, достигавшие почти 100 м по вертикали на протяжении тысячелетий [5]. До сих пор нет ответа на вопрос, как эти колебания возникали – медленно, в течение тысячелетий, или же были и резкие скачки, обусловленные внезапными подвижками в коре в районе бассейнов Каспийского и Аральского морей. Существует гипотеза, что при тектонической подвижке могла понизиться высота Апшеронской гряды в сужении Каспийского моря, что привело к стоку воды в южную котловину, ранее бывшею сухой. При этом уровень воды в море резко упал. Академик Бэр, исследовавший в XIX в. берега северной части Каспия, обнаружил регулярные гряды высотой в несколько метров, гребни которых удалены примерно на 1 км друг от друга, а ось гребней вытянута с востока на запад [6]. Гребни расставлены в шахматном порядке (рис. 1). Бэр выдвинул гипотезу, что при резком понижении уровня воды в Каспии, возникший поток воды сформировал эти гряды. Однако причина формирования гряд потоком воды до сих пор не выяснена [7]. Такие гряды могла сформировать трехмерная стационарная волна, гребни которой также имеют шахматный порядок. В этом случае длина волны должна быть равна расстоянию между гребнями существующих гряд. Проверка этой гипотезы является целью настоящей работы. Для этого в эксперименте установлены основные особенности формирования волн на потоке воды, получена оценка параметров потока воды, рассчитана длина трехмерной волны на поверхности потока, возникшего при понижении уровня Каспийского моря. Расчеты показали, что длина волны близка расстоянию между вершинами гряд Бэра, а скорость размыва соответствует возникшим деформациям дна. Это подтверждает предположенную гипотезу.

АППАРАТУРА И МЕТОДИКА ЭКСПЕРИМЕНТА

Эксперименты проводились в прямом канале с прозрачными стенками. Длина канала – 3.5 м, ширина – 20 см. Наклон дна канала менялся с помощью системы домкратов от 0° до 0.001°. На дне канала лежал слой песка со средним диаметром песчинки 0.2 мм. Канал заполнялся водой до вертикальной отметки $y = $ 7 см ($y = 0$ на дне канала), после чего заслонка на выходе канала резко опускалась. В результате создавался нестационарный поток с увеличивающимся во времени числом Фруда. Форма свободной поверхности и песчаного дна фиксировалась на видеозаписи (скорость записи 25 кадров в секунду). Поле скоростей определялось по перемещению сферических шариков из полистирола диаметром 0.1 см и плотностью 1.05 г ∙ см^–3. Доверительный интервал определения скорости течения не превышал 10% от измеряемой величины для доверительной вероятности 0.67.

ПАРАМЕТРЫ ПОТОКА И СТАЦИОНАРНЫХ ВОЛН ПРИ СЛИВЕ ВОДЫ

Качественная картина процесса слива воды из водохранилища была получена в серии экспериментов. Вода набиралась до уровня 7 см над дном канала. При удалении заслонки возникал поток воды, скорость которого быстро нарастала во времени и менялась вдоль канала. При u > 23.1 см ∙ с^–1, на поверхности потока появлялись стационарные волны [1]. При дальнейшем увеличении скорости течения росли число Фруда, угол наклона свободной поверхности и крутизна стационарных волн. Когда число Фруда превысило значение 0.47, крутизна плоских волн достигла критического значения, при котором плоские волны теряют устойчивость: вместо коротких плоских волн возникли длинные трехмерные волны [3]. На рис. 2 приведен кадр видеозаписи, на котором видна длинная стационарная трехмерная волна. Число Фруда потока составляет примерно 0.7. Трехмерная нелинейная волна имеет резко ассиметричную форму: очень пологий задний склон (на кадре слева, волна бежит навстречу потоку) и очень крутой передний склон (наклон поверхности воды $\frac{{2a}}{{\Delta x}} \approx 0.9$). Такая форма волны хорошо соответствует форме бугров Бэра, имеющих очень крутой северный склон и очень пологий южный склон (волна бежит навстречу потоку с юга на север).

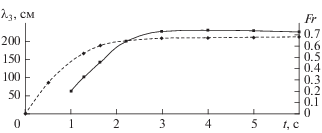
Зависимости числа Фруда потока и длины трехмерной волны от времени, прошедшего от начала процесса слива воды, приведены на рис. 3. Из приведенных данных следует, что число Фруда и длина трехмерной волны быстро растут и достигают максимальных значений $Fr \approx 0.7$ и ${{\lambda }_{3}} \approx 220$ м за интервал времени $0 < t < 2$ с. Затем скорость потока начинает медленно уменьшаться при уменьшении глубины слоя воды. В результате число Фруда и длина волны не меняются и сохраняют максимальные значения в последующие 4 секунды почти до полного слива воды. В период разгона потока длина волны быстро меняется и не успевает сформировать гряды на дне. В основной интервал времени $2 < t < 6$ с длительное воздействие на дно волны постоянной длины позволяет сформироваться песчаной гряде, причем расстояние между гребнями гряды равно длине волны. Полученные результаты проверены для углов наклона дна канала менее 0.001°. Угол берегового склона в зоне расположения бугров Бэра не превышает 10^–4, что позволяет предположить применимость полученных результатов к натурным условиям при тех же числах Фруда.

На основе лабораторных и натурных данных в [2] было показано, что длина трехмерной волны определяется только числом Фруда. Полученная в данном эксперименте зависимость длины трехмерной волны от числа Фруда в интервале значений 0.5 < Fr < 0.71 приведена ниже:

Используя эту зависимость можно определить длину трехмерной волны, которая могла сформировать бугры Бэра. Для этого необходимо оценить глубину и скорость потока, возникающего при падении уровня моря для расчета максимальных значений числа Фруда.

ГЛУБИНА СЛОЯ ВОДЫ НА БЕРЕГОВОМ СКЛОНЕ

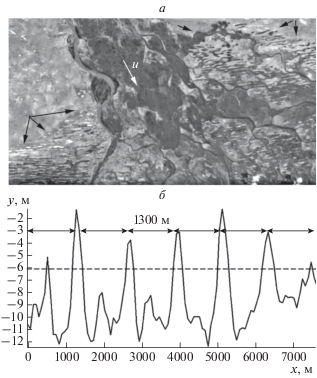
На рис. 1а приведен космический снимок северного берега моря, покрытого буграми Бэра вблизи русла Волги. На снимке гряды имеют вид параллельных полосок, вытянутых с востока на запад. Стрелками показана северная граница этой области, которая почти совпадает с нулевой отметкой абсолютной шкалы высот. Существование четкой границы зоны гряд позволяет заключить, что урез воды располагался вблизи этой границы, т.е. почти совпадал с нулевой отметкой. Так как формирование гряды заключается в появлении размыва под передним крутым склоном волны (в зоне замедления течения), то максимальная высота гребней гряд не может превышать начальную отметку поверхности воды, т.е. нулевую отметку шкалы высот. На рис. 1б приведен профиль гряды на участке длиной 7 км, расположенном в 30 км южнее границы. Профиль получен вдоль вертикального разреза, направленного по нормали к оси гребней и вытянут с юга на север. Из приведенных данных следует, что на участке длиной 7 км существуют регулярные гряды, вершины которых расположены на расстоянии 1300 м друг от друга. Средние отметки вершин гряд расположены на метр ниже уровня моря. Штриховой линией показан уровень, на котором появляется дополнительная нерегулярная деформация берега малой амплитуды. Эта деформация могла возникнуть при обтекании высоких гряд поверхностными потоками при малых расходах воды. Можно принять штриховую линию как нижнюю границу деформации при формировании регулярной гряды. Тогда максимальная глубина слоя воды на деформированной поверхности берега в конце разгона потока не превышала h = 7 м.

ОЦЕНКА СРЕДНЕЙ СКОРОСТИ ТЕЧЕНИЯ

На рис. 4 приведена схема вертикального сечения слоя воды на береговом склоне перед изменением уровня моря. Рассмотрим участок длиной L = 30 км, покрытый водой. Пусть слой воды единичной толщины, имеющий площадь сечения ${{V}_{1}} = \frac{{Lh}}{2},$ опускается на половину глубины h/2. Потенциальная энергия слоя переходит в кинетическую энергию возникающего потока, расходуется на подъем слоя песка единичной толщины, имеющего площадь сечения ${{V}_{s}} = L\Delta y,$ на половину средней высоты гряды $\Delta y$ = 2 м (отсчитывается от штриховой линии на рис. 1б). Потери на вязкое трение обусловлены энергией, затраченной на формирование цилиндрических вихрей в вязком слое потока в зоне замедления течения под передним склоном стационарной волны. Запишем баланс энергии:

где g – ускорение силы тяжести, u – средняя скорость воды на участке при максимальных числах Фруда, $\frac{{{{\rho }_{s}}}}{\rho } = 1.5$ – отношение плотности мокрого песка к плотности воды, $\nu = {{10}^{{ - 6}}}\,\,{{{\text{м}}}^{2}} \cdot {{{\text{с}}}^{{ - 1}}}$ – кинематическая вязкость воды, ${{t}_{с}}$ – время сползания слоя воды на участке, ${{\Omega }_{z}}$ – компонента ротора скорости по поперечной оси в вязком слое потока воды. Скорость в вязком слое потока будем считать линейной функцией вертикальной координаты $u = {{u}_{0}} + \chi y.$ В соответствии с [8] ${{\Omega }_{z}} = \chi = \frac{{4{{u}_{0}}}}{\delta },$ где δ – толщина вязкого слоя. С учетом ${{u}_{0}} \approx \frac{u}{{10}}$ для скорости потока $u > 25\,\,{\text{см}} \cdot {{{\text{с}}}^{{ - 1}}}$ получаем ${{\Omega }_{z}} = \frac{{2{{u}_{0}}}}{{5\delta }}.$ Для приблизительной оценки скорости потока будем считать, что параметры потока не меняются вдоль оси x на участке длиной L, тогда (2) можно записать в следующем виде:

Решение уравнения (3) определяет среднюю скорость потока на участке L при максимальных числах Фруда. Для значений h = 7 м, δ = 0.6 см, $\Delta y$ = 2 м получаем оценку скорости $u = 5.8$ м ∙ с^–1.

Полученные оценки глубины слоя воды и средней скорости течения позволяют рассчитать максимальное число Фруда $Fr = \frac{u}{{\sqrt {gh} }},$ при котором трехмерная волна формирует гряду на дне. Для h = 7 м и $u = 5.8$ м ∙ с^–1 получаем Fr = 0.7. Экспериментальная зависимость длины трехмерной волны от числа Фруда, заданная выражением (1), позволяет определить длину волны для числа Фруда 0.7 и глубины h = 7 м: ${{\lambda }_{3}} = $ 1300 м. Полученное значение совпадает с расстоянием между гребнями гряды Бэра (рис. 1), что свидетельствует в пользу предложенной гипотезы. Однако, чтобы утверждать, что именно эта волна сформировала гряду, надо рассчитать скорость размыва дна и выяснить, могла ли сформироваться гряда на песчаном дне за время существования трехмерной волны.

СКОРОСТЬ РАЗМЫВА ДНА СТАЦИОНАРНОЙ ВОЛНОЙ

Будем считать, что время существования длинной трехмерной волны приблизительно равно времени слива слоя воды на исследуемом участке ${{t}_{c}} = \frac{L}{u} \approx 5000$ с. Размыв идет только в зоне торможения течения под крутым передним склоном гребня стационарной волны. Следуя [8], размыв осуществляется цилиндрическими вихрями, формирующимися в вязком слое потока толщиной δ с периодом T и шагом s между вихрями вдоль оси x [8]. Ось вихрей параллельна поперечной оси z. Будем считать, что параметры течения и вихрей однородны вдоль оси вихрей. Диаметр вихрей составляет $d \approx \frac{2}{3}\delta .$ Вертикальный профиль усредненной по времени скорости в вязком слое (исключая очень тонкий слой у поверхности раздела) можно аппроксимировать функцией $u(y) = {{u}_{s}} + \chi y$ ($y = 0$ у подстилающей поверхности), где $\chi = \frac{{\partial u}}{{\partial y}} = {\text{const,}}$ а ${{u}_{s}} \approx 0.1u.$ В [8] получены полуэмпирические зависимости T и s от u, ${{u}_{x}} = {{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. \kern-0em} {\partial x}},$ безразмерного коэффициента трения C_f и δ:

В соответствии с (4) с увеличением значения $\left| {{{u}_{x}}} \right|$ расстояние между вихрями и период их вылета уменьшается. Для крутого переднего склона трехмерной волны можно записать оценку:

где $\beta $ – тангенс угла наклона поверхности воды. В соответствии с экспериментальными данными верхняя оценка этого параметра для потока при Fr = 0.7 составляет $\left| {{{u}_{x}}} \right| \approx 0.9$ с^–1. Расчет по (4) дает T = 0.16 с и s = 6.7 см для следующих значений параметров: C_f = 0.25 (песок) и $\delta = 0.6$ см.

В соответствии с натурными данными протяженность промоин у крутого склона гряды составляет примерно ${{L}_{{\text{я}}}} = 100$ м. Для средней высоты гряд на исследуемом участке $\Delta y \approx 2{\text{ м}}$ площадь сечения образованной ямы составляет ${{S}_{{\text{я}}}} = 200$ м². Если песок вынесли из промоины цилиндрические вихри, образованные за время ${{t}_{c}},$ то всего вихрей вылетело $N = \frac{{{{L}_{{\text{я}}}}}}{s}\frac{{{{t}_{c}}}}{T}$ штук, а с учетом полученных данных $N = 4.6 \cdot {{10}^{7}}$ штук. В [8] экспериментально установлено, что каждый вихрь может переносить в своем сечении 0.3–0.4 мм² песка. Тогда для формирования ямы указанного выше размера требуется $5 \cdot {{10}^{7}}$ вихрей. Количество вылетевших вихрей оказывается близким количеству вихрей, требуемых для размыва ямы данного размера. Это значит, что трехмерная волна могла сформировать гряду за время своего существования, что доказывает сделанное предположение о формировании бугров Бэра стационарной трехмерной волной.

ЗАКЛЮЧЕНИЕ

Экспериментально исследованы параметры возникающего потока и деформация поверхности воды в водоеме при резком открытии заслонки (плотины). За короткий промежуток времени происходит быстрый рост скорости течения, числа Фруда и угла наклона свободной поверхности воды. Когда скорость течения превышает значение 23.1 см ∙ с^–1, на поверхности потока появляются стационарные волны. При дальнейшем увеличении скорости течения и угла наклона свободной поверхности воды растет крутизна стационарных волн. При достижении критической крутизны нелинейные волны распадаются на длинные трехмерные волны. Число Фруда, скорость потока и длина трехмерной волны быстро достигает максимальных значений. Затем число Фруда и длина трехмерной волны не меняются почти до конца слива воды. Постоянство числа Фруда обусловлено тем, что скорость течения и глубина слоя воды убывают одновременно. За время жизни длинной волны на дне канала формируется гряда, расстояние между гребнями которой равно длине трехмерной волны. При увеличении угла берегового склона характер картины сохраняется, но максимальное число Фруда растет.

Полученные результаты проверены для углов наклона дна канала менее 0.001°. Угол берегового склона в зоне расположения бугров Бэра на северном берегу Каспийского моря не превышает 10^–4, что позволяет предположить применимость полученных результатов к натурным условиям при тех же числах Фруда. На основе натурных данных получена оценка средней скорости потока воды, глубина слоя воды в начальный момент времени, рассчитаны число Фруда и длина трехмерной волны. Проверка показала, что рассчитанная длина трехмерной волны точно соответствует расстоянию между грядами, что подтверждает предложенную гипотезу. Оценка скорости размыва песчаного дна показала, что за время существования трехмерной волны она успевает сформировать существующую систему гряд. Это позволяет утверждать, что существующий грядовый рельеф действительно создан потоком, возникшим при внезапном понижении уровня воды в Каспийском море.