Известия РАН. Серия физическая, 2020, T. 84, № 10, стр. 1416-1421
Энергия связи ядерной материи на языке КХД конденсатов
Е. Г. Друкарев 1, М. Г. Рыскин 1, В. А. Садовникова 1, *
1 Федеральное государственное бюджетное учреждение
“Петербургский институт ядерной физики имени Б.П. Константинова”
Национального исследовательского центра “Курчатовский институт”
Гатчина, Россия
* E-mail: sadovnik@thd.pnpi.spb.ru
Поступила в редакцию 11.05.2020
После доработки 02.06.2020
Принята к публикации 26.06.2020
Аннотация
Мы выражаем параметры нуклонов в симметричной ядерной материи – эффективную массу $m{\text{*}}$, векторную собственную энергию ${{\Sigma }_{V}}$ и энергию связи на нуклон $\mathfrak{P}$ через КХД конденсаты. При включении конденсатов вплоть до размерности d = 6 найдено равновесное состояние ядерной материи для значений нуклонного сигма члена ${{{\sigma }}_{N}} > 41$ МэВ. Равновесие возникает благодаря влиянию релятивистского движения нуклонов на скалярный кварковый конденсат.
ВВЕДЕНИЕ
В этой работе мы продолжаем изучение нуклонных параметров методом правил сумм КХД при конечной плотности, применяя их к ядерной материи. Напомним, что нуклонные правила сумм КХД основываются на дисперсионных соотношениях для функции $\Pi (q)$, описывающей распространение системы с четырехмерным импульсом q и имеющей квантовые числа нуклона (пробного протона). Как в вакууме, так и в среде отправной точкой являются дисперсионные соотношения по ${{q}^{2}}$. Левые части дисперсионных соотношений содержат КХД конденсаты, а правые выражены через параметры наблюдаемых адронов. Обмены сильно коррелированными кварк-антикварковыми парами (мезонами) между пробным протоном и нуклонами материи выражены, таким образом, через обмены слабо коррелированными парами. Дираковская эффективная масса нуклона $m{\text{*}}$ входит в правилах сумм в скалярную структуру функции $\Pi (q)$ и определяется, главным образом, скалярным конденсатом ${\kappa }({\rho })$.
В наших предыдущих работах [1, 2] мы проанализировали ядерную скалярную собственную энергию ${{\Sigma }_{S}}$ и векторную собственную энергию ${{\Sigma }_{V}}$. Мы нашли разумные величины для нуклонных собственных энергий при феноменологической равновесной плотности ${{{\rho }}_{0}}$ и приемлемую ${\rho }$-зависимость этих характеристик. Детали вычислений даны в [3], [4], обзор предыдущих работ представлен в [5].
В нашем подходе нуклонные параметры m* = = m + ΣS (m ‒ масса покоящегося свободного нуклона в вакууме) и ${{\Sigma }_{V}}$ выражены в терминах КХД конденсатов в ядерной материи. Наиболее важны конденсаты низшей размерности d = 3. Это векторный и скалярный кварковые конденсаты ${\nu }({\rho }) = \left\langle {M\left| {\sum\nolimits_i {{{{\bar {q}}}^{i}}} {{{\gamma }}_{0}}{{q}^{i}}} \right|M} \right\rangle $ и ${\kappa }({\rho }) = \left\langle {M\left| {{{\Sigma }_{i}}{{{\bar {q}}}^{i}}{{q}^{i}}} \right|M} \right\rangle .$ Здесь $\left| M \right\rangle $ – вектор состояния ядерной материи, сумма выполняется по цветам кварков. Векторный конденсат модельно независим: ${\nu }(q) = {{n}_{{\text{v}}}}{\rho }$, где ${{n}_{{\text{v}}}}$ – число валентных кварков в нуклоне (${{n}_{{\text{v}}}}$ = 3). Вычисление скалярного конденсата требует модельных представлений для ядерной материи.
Во всех предыдущих публикациях, использующих правила сумм КХД, на первом шаге ядерная материя рассматривалась как газ свободных невзаимодействующих нуклонов. Пренебрегая фермиевским движением нуклонов, мы находим
(1)
${\kappa }({\rho }) = {\kappa }(0) + {{{\kappa }}_{N}}{\rho };\,\,\,\,{{{\kappa }}_{N}} = \left\langle {N\left| {\sum\limits_i {\bar {q}} q} \right|N} \right\rangle .$Здесь ${\kappa (0)} = \left\langle {0\left| {\bar {u}u + \bar {d}d} \right|0} \right\rangle $. Стандартно используемая величина ${\kappa (0)} = 2{{( - 240\,\,{\text{МэВ}})}^{3}}$ [6]. Нуклонный матричный элемент ${{{\kappa }}_{N}} = \frac{{{{{\sigma }}_{N}}}}{{{{m}_{q}}}}, $ где ${{m}_{q}} = {{({{m}_{u}} + {{m}_{d}})} \mathord{\left/ {\vphantom {{({{m}_{u}} + {{m}_{d}})} 2}} \right. \kern-0em} 2}$, а ${{{\sigma }}_{N}}$ $ - $ нуклонный сигма член. Тогда
Обычно используют оценку σN ≈ 45 МэВ [7]. Однако некоторые экспериментальные данные допускают величину ${{{\sigma }}_{N}} \approx 65$ МэВ [8]. Скалярный конденсат с учетом нуклонных взаимодействий можно записать как
где вклад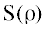 определяется нуклонными взаимодействиями. Ведущий вклад в
определяется нуклонными взаимодействиями. Ведущий вклад в 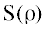 дает пионное облако [5]. Расчеты с использованием правил сумм воспроизвели величины нуклонных собственных
энергий [1], [3] и иерархию вкладов многочастичных сил. Но может ли подход правил сумм КХД описать
насыщение ядерной материи?
дает пионное облако [5]. Расчеты с использованием правил сумм воспроизвели величины нуклонных собственных
энергий [1], [3] и иерархию вкладов многочастичных сил. Но может ли подход правил сумм КХД описать
насыщение ядерной материи?
В ранних работах пионное облако рассматривалось как создаваемое однопионным обменным
взаимодействием. Вклад 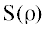 уменьшает второй член в правой части (3). Отсюда возникает некоторый добавочный нелинейный
вклад, соответствующий притяжению в скалярном канале. Оценка [5] показала, что этот вклад мог бы вызвать насыщение. Позже выполнены более строгие
расчеты
уменьшает второй член в правой части (3). Отсюда возникает некоторый добавочный нелинейный
вклад, соответствующий притяжению в скалярном канале. Оценка [5] показала, что этот вклад мог бы вызвать насыщение. Позже выполнены более строгие
расчеты 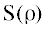 на основе киральной теории возмущений [9, 10, 11]. Расчеты в рамках правил сумм КХД, выполненные в [10], дают разумные величины $\left| {\mathfrak{P}\left( {\rho } \right)} \right| \approx $ 10–20 МэВ для энергии связи на нуклон $\mathfrak{P}({\rho )}$. Однако функция $\mathfrak{P}({\rho )}$ не имеет минимума. Таким образом, описываемый подход не дает насыщения.
на основе киральной теории возмущений [9, 10, 11]. Расчеты в рамках правил сумм КХД, выполненные в [10], дают разумные величины $\left| {\mathfrak{P}\left( {\rho } \right)} \right| \approx $ 10–20 МэВ для энергии связи на нуклон $\mathfrak{P}({\rho )}$. Однако функция $\mathfrak{P}({\rho )}$ не имеет минимума. Таким образом, описываемый подход не дает насыщения.
В предлагаемой работе мы используем другую версию правил сумм КХД при конечной плотности. Мы полагаем, что состояние $\left| M \right\rangle $ образовано взаимодействующими релятивистскими нуклонами, помещенными в КХД – вакуум. Благодаря нуклонному взаимодействию каждый нуклон получает векторную и скалярную собственную энергию ${{\Sigma }_{V}}$ и ${{\Sigma }_{S}}$. Мы вычислим энергию связи $\mathfrak{P}({\rho )}$, используя правила сумм КХД, и проверим, описывает ли данный подход насыщение.
СКАЛЯРНЫЙ КОНДЕНСАТ В СИСТЕМЕ РЕЛЯТИВИСТСКИХ ВЗАИМОДЕЙСТВУЮЩИХ НУКЛОНОВ
Для вычисления конденсата мы рассмотрим плотность энергии, отвечающую гамильтониану КХД $H(x) = {{m}_{u}}\bar {u}(x)u(x) + {{m}_{d}}\bar {d}(x)d(x) + ...$
Точки обозначают вклады, которые не зависят от масс легких кварков ${{m}_{u}}$ и ${{m}_{d}}$. Скалярный конденсат может быть записан как
(4)
${\kappa (\rho )} = \left\langle {M\left| {\frac{{\partial H}}{{\partial {{m}_{q}}}}} \right|M} \right\rangle .$Теорема Гельмана–Фейнмана позволяет связать скалярный конденсат с плотностью энергии материи $\mathcal{E}$
(производные от векторов состояния $\left| M \right\rangle $ и $\left\langle M \right|$ сокращаются). Тогда
Для свободного нуклона в покое мы приходим к (2) с ${{{\sigma }}_{N}} = {{m}_{q}}({{\partial m} \mathord{\left/ {\vphantom {{\partial m} {\partial {{m}_{q}}}}} \right. \kern-0em} {\partial {{m}_{q}}}}).$
Для ферми–газа релятивистских нуклонов
где(7)
${{F}_{0}}({\rho }) = 4\int {\frac{{{{d}^{3}}p}}{{{{{(2{\pi })}}^{3}}}}} \frac{{m {\theta }({{p}_{F}} - p)}}{{\sqrt {{{m}^{2}} + {{p}^{2}}} }} ,$а ${{p}_{F}}$ обозначает импульс Ферми.
Теперь мы должны вычислить плотность энергии $\mathcal{E}$ для ядерной материи. Волновое уравнение для нуклона с четырех-импульсом p может быть записано как
Биспинор u нормирован условием $u{{{\gamma }}_{0}}u = 1.$ Таким образом, энергия нуклона есть
(8)
${{p}_{0}} = E(\left| {\vec {p}} \right|) = \bar {u}({{p}_{i}}{{{\gamma }}^{i}} + m*)u + {{\Sigma }_{V}}\bar {u}{{{\gamma }}_{0}}u,$Если учитывать только 2N взаимодействие нуклона, то плотность энергии есть
(9)
$\begin{gathered} \mathcal{E} = 4\int {\frac{{{{d}^{3}}p}}{{{{{(2{\pi })}}^{3}}}}} {\theta }({{p}_{F}} - p) \Phi (p); \\ \Phi (p) = \bar {u}({{p}_{i}}{{{\gamma }}^{i}} + m)u + \frac{{{{\Sigma }_{V}}}}{2}\bar {u}{{{\gamma }}_{0}}u + \frac{{{{\Sigma }_{S}}}}{2}\bar {u}u; \\ {{\Sigma }_{S}} = m{\text{*}} - m . \\ \end{gathered} $Напомним, что в ядерной материи собственные энергии ${{\Sigma }_{V}}$ и ${{\Sigma }_{S}}$ не зависят от p. Учитывая только двухнуклонные (2N) взаимодействия, получим
(10)
$\mathcal{E} = 4\int {\frac{{{{d}^{3}}p}}{{{{{(2{\pi })}}^{3}}}}} {\theta }({{p}_{F}} - p) E{\text{*}}(p) - \frac{{{{\Sigma }_{S}}}}{2}{\rho }F({\rho }) + \frac{{{{\Sigma }_{V}}}}{2}{\rho }.$Здесь
(11)
$\begin{gathered} F({\rho }) = \frac{4}{{\rho }}\int {\frac{{{{d}^{3}}p}}{{{{{(2{\pi })}}^{3}}}}} {\theta }({{p}_{F}} - p)\frac{{m{\text{*}} }}{{E{\text{*}}(p)}} = \\ = \frac{2}{{{{{\pi }}^{2}}{\rho }}}\int\limits_0^{{{p}_{F}}} {dp{{p}^{2}}} \frac{{m{\text{*}} }}{{E{\text{*}}(p)}}. \\ \end{gathered} $Отметим, что $F({\rho })$ = 1 в нерелятивистском пределе ${{p}_{F}} \ll m{\text{*}}$. Плотность энергии в скалярно-векторной модели Валечки в приближении среднего поля
(12)
$\mathcal{E} = 4\int {\frac{{{{d}^{3}}p}}{{{{{(2{\pi })}}^{3}}}}} {\theta }({{p}_{F}} - p)E{\text{*}}(p) + \frac{{m_{S}^{2}\varphi _{0}^{2}}}{2} + \frac{{m_{V}^{2}V_{0}^{2}}}{2},$(см. уравнение (5.43) в [12]) принимает форму (10), если поля ${{\varphi }_{0}}$ и ${{V}_{0}}$ выражены через собственные энергии нуклонов (уравнения (5.35) и (5.36) в [12]).
Мы предполагаем, что основная зависимость энергии $\mathcal{E}$ от массы кварка ${{m}_{q}}$ заключена в массе нуклона m. Это позволяет положить ${{\partial {{\Sigma }_{S}}} \mathord{\left/ {\vphantom {{\partial {{\Sigma }_{S}}} {\partial {{m}_{q}}}}} \right. \kern-0em} {\partial {{m}_{q}}}}$ = = ${{\partial {{\Sigma }_{V}}} \mathord{\left/ {\vphantom {{\partial {{\Sigma }_{V}}} {\partial {{m}_{q}}}}} \right. \kern-0em} {\partial {{m}_{q}}}} = 0.$ Таким образом, ${{\partial m{\text{*}}} \mathord{\left/ {\vphantom {{\partial m{\text{*}}} {\partial {{m}_{q}}}}} \right. \kern-0em} {\partial {{m}_{q}}}} = {{\partial m} \mathord{\left/ {\vphantom {{\partial m} {\partial {{m}_{q}}}}} \right. \kern-0em} {\partial {{m}_{q}}}}.$ Предположение основывается на относительно малом вкладе нуклонного взаимодействия в конденсаты ${\kappa }({\rho })$, полученном в [9‒11]. Тогда, используя (5), мы получаем
(13)
${\kappa }({\rho }) = {\kappa }(0) + \frac{{{\sigma }_{N}^{{eff}}}}{{{{m}_{q}}}}{\rho },\,\,\,\,{\sigma }_{N}^{{eff}}({\rho }) = {{{\sigma }}_{N}}F({\rho }).$Функция $F({\rho })$ определена формулой (11). Сравнивая с (6), мы видим, что (13) описывает скалярный конденсат в ферми-газе нуклонов с массой $m{\text{*}}$. Функция $F({\rho })$ также связывает барионную и скалярные плотности ${\rho }$ и ${{{\rho }}_{S}}$: ${{{\rho }}_{S}} = F({\rho }) {\rho }$ в приближении среднего поля скалярно-векторной модели ядерной материи.
САМОСОГЛАСОВАННОЕ УРАВНЕНИЕ ДЛЯ ЭФФЕКТИВНОЙ МАССЫ
Напомним, что имеется три уравнения правил сумм, соответствующие трем структурам $\hat {q}$, $\hat {p}$ и I волнового уравнения для пробного протона.
После преобразования Бореля правила сумм принимают вид:
(14)
$\begin{gathered} {{\mathcal{L}}^{q}}({{M}^{2}},W_{m}^{2};{\eta }) = {{\Lambda }_{m}}({{M}^{2}}); \\ {{\mathcal{L}}^{I}}({{M}^{2}},W_{m}^{2};{\eta }) = m{\text{*}}{{\Lambda }_{m}}({{M}^{2}}); \\ {{\mathcal{L}}^{P}}({{M}^{2}},W_{m}^{2};{\eta }) = - \frac{{{{\Sigma }_{V}}}}{m}{{\Lambda }_{m}}({{M}^{2}}). \\ \end{gathered} $Здесь ${\eta }({\rho })$ ‒ набор КХД конденсатов в ядерной материи с барионной плотностью ρ. Левые части также зависят от эффективного порога континуума $W_{m}^{2}$, который аппроксимирует высшие возбужденные состояния.
Правые части уравнений (14) содержат эффективную массу пробного протона $m{\text{*}}$ (или скалярную собственную энергию ${{\Sigma }_{S}} = m{\text{*}} - m$) и его собственную энергию ${{\Sigma }_{V}}$. Они умножаются на фактор ${{\Lambda }_{m}} = {\lambda }_{m}^{2}\exp ({{ - m_{m}^{2}} \mathord{\left/ {\vphantom {{ - m_{m}^{2}} {{{M}^{2}}}}} \right. \kern-0em} {{{M}^{2}}}})$, где ${\lambda }_{m}^{2} = 32{{{\pi }}^{4}}{\lambda }_{{Nm}}^{2}$, величина ${\lambda }_{{Nm}}^{2}$ есть вычет в нуклонном полюсе. Положение полюса ${{m}_{m}}$ выражается в терминах характеристик пробного нуклона $m{\text{*}}$ и ${{\Sigma }_{V}}$. Нуклонные параметры $m{\text{*}}$ и ${{\Sigma }_{V}}$, а также вычеты ${\lambda }_{m}^{2}$ и порог континуума $W_{m}^{2}$ являются неизвестными, которые определяются путем решения системы уравнений (14).
Если включены только конденсаты низших размерностей $\nu ({\rho })$ и ${\kappa }({\rho })$, тогда ${{\mathcal{L}}^{{ q}}}$ и ${{\mathcal{L}}^{P}}$ зависят только от $\nu ({\rho })$, а ${{\mathcal{L}}^{I}}$ зависит только от ${\kappa }({\rho })$. Используя (14), можно записать
(15)
$\frac{{{{\mathcal{L}}^{I}}({{M}^{2}},W_{m}^{2};{\kappa }({\rho }))}}{{{{\mathcal{L}}^{q}}({{M}^{2}},W_{m}^{2};{\kappa }({\rho }))}} = m{\text{*}}({\rho }).$Поскольку в нашем подходе ${\kappa (\rho )}$ зависит от $m{\text{*}}({\rho })$, то (15) есть самосогласованное уравнение для эффективной массы $m{\text{*}}$. Уравнения для структур ${{\mathcal{L}}^{{ q}}}$ и ${{\mathcal{L}}^{P}}$ просто выражают нуклонные параметры в терминах КХД конденсатов. Это справедливо и для конденсатов более высоких размерностей пока мы включаем только 2N взаимодействия.
ПОСЛЕДОВАТЕЛЬНОЕ ВКЛЮЧЕНИЕ КОНДЕНСАТОВ
Мы будем последовательно включать конденсаты высших размерностей и радиационные поправки. Кроме вычисления векторной собственной энергии ${{\Sigma }_{V}}$ и эффективной массы $m{\text{*}}$ мы также найдем среднюю энергию на нуклон $\mathfrak{P}\left( {\rho } \right) = \frac{\mathcal{E}}{{\rho }} {\rho } - m.$ Включая только конденсаты размерности d = 3, т.е. векторный и скалярный конденсаты, и логарифмические радиационные поправки мы получаем для ${{{\sigma }}_{N}}$ = 65 МэВ: ${{\Sigma }_{S}}$ = –290 МэВ и ${{\Sigma }_{V}}$ = 227 МэВ при плотности ${\rho }$ равной феноменологической равновесной величине ${{{\rho }}_{0}} = $ 0.17 фм–3. Мы получаем $\mathfrak{P}({\rho }) > 0$ (см. рис. 1а), и материя не связана. Поскольку $\left| {{{\Sigma }_{S}}} \right|$ растет с величиной ${{{\sigma }}_{N}}$, этот результат тем более справедлив для меньших значений ${{{\sigma }}_{N}}$.
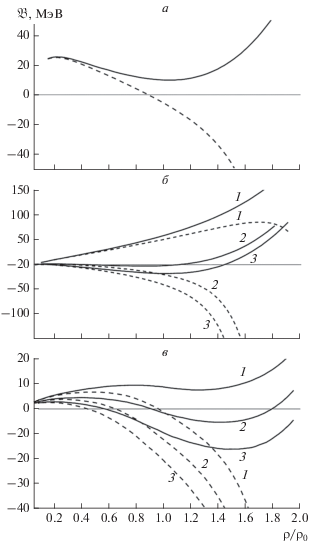
Рис. 1.
Зависимость средней энергии связи на нуклон $\mathfrak{P}(\rho )$ от плотности ${\rho }$. По вертикальной оси отложено значение $\mathfrak{P}(\rho )$ в МэВ. Результатам, полученным для $F({\rho })$ = 1 в формуле (13) соответствует штрихованная кривая. Сплошная кривая соответствует ${\kappa }({\rho })$, определенному формулой (13) с учетом функции $F({\rho })$. а – Учет лишь конденсатов размерности d = 3, ${{{\sigma }}_{N}}$ = = 65 МэВ; б – учтены ведущие нелогарифмические радиационные поправки и конденсаты размерности $d \leqslant 4$, кривые 1, 2, 3 получены, соответственно, для значений ${{{\sigma }}_{N}} = 45,61,65$ МэВ соответственно; в – включены конденсаты размерности $d \leqslant 6$, кривые 1, 2, 3 соответствуют расчетам с ${{{\sigma }}_{N}} = 40,42,43.6$ МэВ.
Дальше мы включаем радиационные поправки и конденсаты с d = 4 и ведущие нелогарифмические радиационные поправки. Имеется несколько вкладов размерности d = 4. Наиболее важны глюонный конденсат и нелокальный векторный конденсат $\left\langle {M\left| {\bar {q}(0){{{\gamma }}_{0}}q(x)} \right|M} \right\rangle $. Последний определяется, в основном, извлекаемым из эксперимента вторым моментом нуклонной структурной функции ${{M}_{2}} = 0.32$.
Прямые вычисления показывают, что $\mathfrak{P}(\rho )$ приобретает минимум, если ${{{\sigma }}_{N}} \geqslant $ 60 МэВ (см. рис. 1б). Величина плотности в минимуме ${{{\rho }}_{{eq}}}$ очень близка к феноменологической равновесной величине ${{{\rho }}_{0}}$ при ${{{\sigma }}_{N}} \approx 65$ МэВ. Мы получили ${{{\rho }}_{{eq}}} = 0.95 {{{\rho }}_{0}}$ при ${{{\sigma }}_{N}}$ = 64.5 МэВ и ${{\mathfrak{P}}_{{min}}}$ = –15.8 МэВ. Заметим, что равновесные состояния возникают благодаря влиянию релятивистского движения нуклонов на скалярный кварковый конденсат. Это приводит к опусканию кривой $\mathfrak{P}(\rho )$ при ${{{\sigma }}_{N}} \approx $ 65 МэВ (см. сплошную кривую на рис. 1б). Включение множителя $F({\rho })$ замедляет падение $m{\text{*}}({\rho })$. В точке равновесия ${{\Sigma }_{S}}$ = –418 МэВ и ${{\Sigma }_{V}}$ = 334 МэВ. Отметим, что величина нерелятивистской одночастичной потенциальной энергии $U = {{\Sigma }_{S}} + {{\Sigma }_{V}} = - 84$ МэВ близка к величине, полученной в точке равновесия в модели Валечки $U = - 90$ МэВ.
Вычисление вкладов конденсатов размерности d = 6, из которых наиболее важны четырехкварковые конденсаты, требуют модельных представлений о структуре нуклона. Мы воспользуемся релятивистской кварковой моделью, ранее применявшейся нами в [1‒5]. Нуклон рассматривается как система трех релятивистских кварков, движущихся в эффективном статическом поле. Кварки также обмениваются пионами, что обеспечивает киральную симметрию. Поскольку мы вычисляем вклады 2N взаимодействий, то должны быть включены только конфигурации, в которых все четыре кварка действуют на один и тот же нуклон материи.
Теперь в материи возникает равновесное состояние при ${{{\sigma }}_{N}}$ > 41.2 МэВ (см. рис. 1в). Как в предыдущем случае и по той же причине равновесные состояния отсутствуют, есть положить $F({\rho })$ = 1.
Мы получаем ${{\mathfrak{P}}_{{\min }}}$ = –16.0 МэВ при ${{{\sigma }}_{N}}$ = = 43.6 МэВ. Значение ${{{\sigma }}_{N}}$ = 43.6 МэВ близко к стандартному. Соответствующая равновесная плотность составляет ${{{\rho }}_{{eq}}} = 1.46 {{{\rho }}_{0}}$. В точке равновесия ${{\Sigma }_{S}}$ = –482 МэВ. Таким образом, ${{\Sigma }_{S}}$ в точке равновесия в нашем подходе и в модели Валечки различаются примерно на 70 МэВ. Величина векторной собственной энергии ${{\Sigma }_{V}}$ = 387 МэВ, превышая результат модели Валечки на 65 МэВ. В равновесии одночастичная потенциальная энергия $U = - 95$ МэВ очень близка к результату модели Валечки $U = - 90$ МэВ.
На рис. 2а показана зависимость ${{\mathfrak{P}}_{{\min }}}$ от ${{{\sigma }}_{N}}$. Зависимость ${{{\rho }}_{{eq}}}$ от ${{{\sigma }}_{N}}$ представлена на рис. 2б.
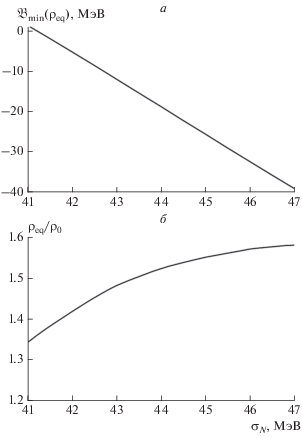
Рис. 2.
Зависимость средней энергии связи на нуклон в равновесном состоянии ${{\mathfrak{P}}_{{\min }}}({{\rho }_{{eq}}})$ (а) и равновесной плотности ${{{\rho }}_{{eq}}}$ (б) от величины ${{{\sigma }}_{N}}$. Включены ведущие радиационные поправки первого порядка и конденсаты размерности $d \leqslant 6$.
Нуклонные параметры $m{\text{*}}$ и ${{\Sigma }_{V}}$ определяются, в основном, конденсатами размерности d = 3. Включение конденсатов высших размерностей делает результаты более точными. Однако энергия связи испытывает существенные изменения. Она приобретает минимум при отрицательных значениях, т.е. включение конденсатов высших размерностей приводит к равновесному состоянию материи. Это показано на рис. 3, где представлены результаты для значения ${{{\sigma }}_{N}}$ = 45 МэВ.
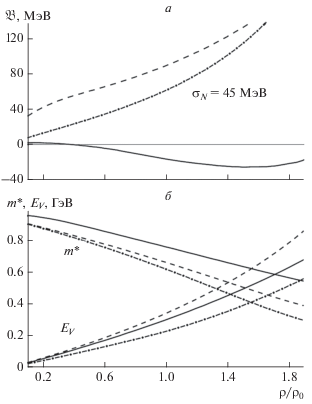
Рис. 3.
Сравнение энергии связи на нуклон $\mathfrak{P}(\rho )$ (а) и нуклонных параметров $m{\text{*}}({\rho })$ и ${{\Sigma }_{V}}({\rho })$ (б), вычисленных с конденсатами $d \leqslant 3$ (штрихованная кривая), $d \leqslant 4$ (штрихпунктирная кривая), $d \leqslant 6$ (сплошная кривая); ${{{\sigma }}_{N}} = 45$ МэВ.
ЗАКЛЮЧЕНИЕ
Мы вычислили нуклонные параметры в симметричной ядерной материи, используя метод правил сумм КХД при конечной плотности. Вычислена также средняя энергия на нуклон $\mathfrak{P}$. Эффективная масса нуклона $m{\text{*}}$, векторная собственная энергия ${{\Sigma }_{V}}$ и энергия связи на нуклон $\mathfrak{P}(\rho )$ выражены через КХД конденсаты. Учитывались только вклады, соответствующие 2N силам. Анализ поведения $\mathfrak{P}(\rho )$ позволил нам исследовать равновесные состояния материи. В настоящей работе мы учитываем лишь двухнуклонные взаимодействия.
Конденсаты низшей размерности (d = 3) – это усредненные по ядерной материи значения векторных и скалярных кварковых операторов. Вычисления скалярного конденсата требует определенных предположений о структуре материи. Мы рассматриваем материю как релятивистскую систему взаимодействующих нуклонов. Это отличается от предыдущих подходов к правилам сумм КХД, где поляризационные операторы рассматривались в системе нерелятивистских свободных нуклонов.
При вычислении скалярного конденсата мы предполагаем, что зависимость плотности энергии от масс кварков определяется массой нуклона.
Мы стартуем с конденсатов размерности d = 3, последовательно добавляя конденсаты больших размерностей. Если учесть только конденсаты размерности d = 3, то энергия связи положительна и равновесные состояния отсутствуют. При учете конденсатов размерности d = 4 и ведущих нелогарифмических радиационных поправок, равновесное состояние возникает лишь при больших значениях ${{{\sigma }}_{N}}$. Для ${{{\sigma }}_{N}}$ = 65 МэВ равновесная плотность очень близка к эмпирическому значению ${{{\rho }}_{{eq}}} = 0.99 {{{\rho }}_{0}}$. Средняя энергия на нуклон ${{\mathfrak{P}}_{{\min }}}({{{\rho }}_{{eq}}})$ = –12.7 МэВ. Величины $m{\text{*}}$ и ${{\Sigma }_{V}}$ близки к значениям, полученным в модели Валечки. Учет четырехкварковых конденсатов (d = 6) приводит к равновесному состоянию материи для ${{{\sigma }}_{N}}$ > 41 МэВ. Состояние, в котором ${{\mathfrak{P}}_{{\min }}}({{{\rho }}_{{eq}}})$ = = –16.0 МэВ, реализуется при значении ${{{\sigma }}_{N}}$, близком к общепринятому ${{{\sigma }}_{N}}$ = 43.6 МэВ, причем ${{{\rho }}_{{eq}}} = 1.46 {{{\rho }}_{0}}$.
Заметим, что пренебрегая влиянием релятивистского движения нуклонов, составляющих материю, на скалярный кварковый конденсат, мы не получаем равновесного состояния. Таким образом, в нашем подходе так же, как в модели Валечки, насыщение представляет собой релятивистский эффект.
Список литературы
Друкарев Е.Г., Рыскин М.Г., Садовникова В.А. // Изв. РАН. Cер. физ. 2017. Т. 81. С. 1334; Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // Bull. Russ. Acad. Sci. Phys. 2017. V. 81. P. 1192.
Друкарев Е.Г., Рыскин М.Г., Садовникова В.А. // Изв. РАН. Cер. физ. 2019. Т. 83. С. 1273; Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // Bull. Russ. Acad. Sci. Phys. 2019. V. 83. P. 1164.
Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // Nucl. Phys. A. 2017. V. 959. P. 129.
Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // Nucl. Phys. A. 2017. V. 968. P. 350.
Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // ЯФ. 2011. T. 74. C. 1; Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // Phys. Atom. Nucl. 2012. V. 75. P. 34.
Ioffe B.L., Lipatov L.N., Fadin V.S. Quantum chromodynamics. Cambridge: Cambridge Univ. Press, 2010.
Gasser J., Leutwyller H., Sainio M.E. // Phys. Lett. B. 1991. V. 253. P. 252.
Gubler P., Satow D. // Prog. Part. Nucl. Phys. 2019. V. 106. P. 1.
Lutz M., Friman B., Appel C. // Phys. Lett. B. 2000. V. 474. P. 7.
Kaiser N., de Homont P., Weise W. // Phys. Rev. C. 2008. V. 77. Art. № 025204.
Goda S., Jido D. // Phys. Rev. C. 2013. V. 88. Art. № 065204.
Serot B.D., Walechka J.D. // Adv. Nucl. Phys. 1986. V. 16. P. 1.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая