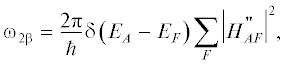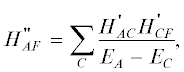Известия РАН. Серия физическая, 2020, T. 84, № 10, стр. 1406-1412

ВВЕДЕНИЕ

Теория ${\beta }$-распадов атомных ядер была построена в 1933 году Ферми [1] при введении им нового вида фундаментального взаимодействия – слабого взаимодействия, современное представление о структуре которого представлено, например, в работах [2, 3]. В настоящее время известны три вида ${\beta }$-распадов: ${{{\beta }}^{ - }}$, ${{{\beta }}^{ + }}$ и электронный захват $EC$, схемы которых имеют вид:

где $\left( {A,Z} \right)$ и $\left( {A,Z \pm 1} \right)$ – родительское и появляющиеся при β-распадах дочерние ядра, ${{e}^{ - }}\left( {{{e}^{ + }}} \right)$ – электрон (позитрон), ${{\nu }_{e}}~\left( {{{{\tilde {\nu }}}_{e}}} \right)$ – нейтрино (антинейтрино). Закон сохранения энергии для ${{{\beta }}^{ - }}$-распада представляется формулой: где теплота ${{Q}_{{{{{\beta }}^{ - }}}}}$ рассматриваемого ${{{\beta }}^{ - }}$-распада и суммарная кинетическая энергия ${{T}_{{{{{\beta }}^{ - }}}}}~$ двух вылетающих легких частиц определяются формулами:

причем $E\left( {A,Z} \right)$ и $E\left( {A,~Z + 1} \right)$ – внутренние энергии родительского $\left( {A,Z} \right)$ и дочернего $\left( {A,~Z + 1} \right)$ ядер. Закон сохранения энергии для ${{{\beta }}^{ + }}$-распада представляется формулой (2) при учете того, что ${{T}_{{{{{\beta }}^{ - }}}}} = {{T}_{{{{{\beta }}^{ + }}}}}$, а теплота ${{Q}_{{{{{\beta }}^{ + }}}}}$ имеет вид:

В случае же электронного захвата закон сохранения энергии также может быть представлен формулой (2), в которой энергия ${{T}_{{{{{\beta }}^{ - }}}}}$ заменяется на энергию ${{T}_{{EC}}}$, которая определяется формулой (4) при исключении из ее правой части энергии позитрона, а$~{\text{теплота}}~{{Q}_{{{{{\beta }}^{ - }}}}}$ определяется как:

Уже в 1935 г. М. Гепперт-Майер в работе [4] впервые указала на возможность процесса двухнейтринного $2{{{\beta }}^{ - }}$-распада, схема распада которого имеет вид:

а закон сохранения энергии представляется формулой:

В формуле (8) ${{Q}_{{2{{\beta }^{ - }}}}}$ – теплота рассматриваемого $2{{\beta }^{ - }}$-распада и ${{T}_{{2{{\beta }^{ - }}}}}$ – суммарная кинетическая энергия четырех вылетающих легких частиц, определяемая как:

причем энергии ${{T}_{1}}$ и ${{T}_{2}}$ для первой ($e_{1}^{ - }~,~{{\tilde {\nu }}_{1}}$) и второй ($e_{2}^{ - }~,~{{\tilde {\nu }}_{2}}$) пар легких частиц определяются формулами типа (4). Аналогичные схемы распада и формулы закона сохранения энергии можно построить и для двойных бета-распадов типа $2{{\beta }^{ + }}$; ${{\beta }^{ + }},EC$; $EC,EC$ при использовании формул (2)–(6).

Первое наблюдение двухнейтринного $2{{\beta }^{ - }}$-распада ядра ¹³⁰Те было проведено на основе геохимического эксперимента [5], а уже к 90-му году XX века наблюдались двухнейтринные $2{{\beta }^{ - }}$-распады в прямых (счетчиковых) экспериментах. К настоящему времени экспериментальные и теоретические исследования двойных ${\beta }$-распадов ядер проведены для заметного круга ядер.

Теория $2{\beta }$-распада родительского ядра $\left( {A,Z} \right)$ была развита в работе [6], при использовании теории квантовых переходов под влиянием возмущения, не зависящего от времени [7], и получена формула для вероятности ${{\omega }_{{2\beta }}}$ указанного распада в единицу времени, при использовании формулы второго порядка теории возмущений по гамильтониану $H{\kern 1pt} '$ слабого взаимодействия:

где

а матричные элементы $H_{{AC}}^{'}$ и $H_{{CF}}^{'}$ имеют вид:

В формуле (13) ${{{\Psi }}_{A}}$, ${{{\Psi }}_{C}}$ и ${{{\Psi }}_{F}}$ – волновые функции родительского ядра A, промежуточного ядра C, возникающего после ${{{\beta }}_{1}}$-распада родительского ядра и конечного ядра F, возникающего после ${{{\beta }}_{2}}$-распада промежуточного ядра C, а ${{{\Phi }}_{A}}$, ${{{\Phi }}_{C}}$ и ${{{\Phi }}_{F}}$ – волновые функции легких частиц, фигурирующих в процессе рассматриваемого $2\beta $-распада совместно с ядрами A, C, F. Следует подчеркнуть, что вероятность ${{\omega }_{{2\beta }}}$ указанного распада в единицу времени связана с шириной этого распада соотношением:

Полученные формулы (11)–(14) были использованы [2, 3] для расчетов ширин $2{\beta }$‑распадов при выборе различных форм гамильтониана $H{\kern 1pt} '$ слабого взаимодействия.

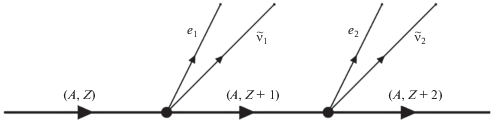
Полученным выше формулам можно поставить в соответствие диаграмму Фейнмана (см. рис. 1), описывающую амплитуду ширины (14) $2\beta $-распада родительского ядра. Вершинные части диаграммы Фейнмана (см. рис. 1) связаны с амплитудами ширин ${\beta }$-распада родительского и промежуточного ядер, определяемых матричными элементами слабого взаимодействия типа $H_{{AC}}^{{\text{'}}}$ и $H_{{CF}}^{{\text{'}}}$, а линия со стрелкой и верхним индексом $\left( {A,Z + 1} \right)$ представляет функцию Грина $G\left( {A,Z + 1} \right)$ промежуточного ядра $\left( {A,~Z + 1} \right)$, пропорциональную величине ${{\left( {{{E}_{A}} - {{E}_{C}}} \right)}^{{ - 1}}}$ формулы (12), которая в силу свойств членов второго порядка теории возмущений по потенциалу $H{\kern 1pt} '$ не имеет полюсного характера.

Целью настоящей работы является дальнейшее развитие теории двойных ${\beta }$-распадов ядер при использовании результатов, полученных при построении теории двухпротонных распадов ядер [8–10]. При этом особое внимание будет уделено выделению двух типов $2{\beta }$-распадов ядер: виртуальным распадам, реализующихся для большинства ядер, и $2{\beta }$-распадов обусловленных следующими друг за другом по времени реальными одинарными β-распадами родительского и возникающего при его ${\beta }$-распаде промежуточного ядер.

1. $2{\beta }$-РАСПАДЫ ЯДЕР КАК ПОСЛЕДОВАТЕЛЬНЫЕ ДВУХСТУПЕНЧАТЫЕ ПРОЦЕССЫ

Если исключить из рассмотрения для двухнейтринных $2{\beta }$-распадов ядер, включающих $2{{\beta }^{ - }}$; $2{{\beta }^{ + }}$; ${{{\beta }}^{ + }},EC$ и $EC,EC$ распады, как не реализуемый физически одновременный вылет из родительского ядра $\left( {A,Z} \right)$ двух, трех или четырех легких частиц, то теорию указанных $2\beta $-распадов можно построить при использовании результатов развитой в работах [8–10] теории последовательных двухступенчатых 2p-распадов ядер. Дальнейшее рассмотрение проведем на примере последовательного двухступенчатого $2{{\beta }^{ - }}$-распада ядер, амплитуда ширины которого, как и в случае, соответствующем рассмотренному во введении представлению ширины $2{{\beta }^{ - }}$-распада при использовании второго порядка теории возмущения по гамильтониану слабого взаимодействия [6], определяется диаграммой Фейнмана (см. рис. 1). На данной диаграмме черными кружочками представлены вершинные части, пропорциональные амплитудам ширин одинарных ${{{\beta }}^{ - }}$-распадов родительского и дочернего ядер, которые рассчитываются через матричные элементы гамильтониана $H{\kern 1pt} '$ слабого взаимодействия, а линия со стрелкой и индексом $\left( {A,Z + 1} \right)$ соответствует одночастичной функции Грина $G\left( {A,Z + 1} \right)$ промежуточного ядра. Эту функцию в более общем случае, чем случай рассмотренный во введении, можно представить формулой:

где ${{{\Psi }}_{i}}$ – волновая функция i-го состояния промежуточного ядра, которое для упрощения обозначается индексом ${{\left( {Z + 1} \right)}_{i}}$, ${{Q}_{{\beta _{1}^{ - }i}}}$ – теплота $~\beta _{1}^{ - }$-распада родительского ядра с образованием $i$-го состояния промежуточного ядра, определяемая формулой (3), в которой в качестве величины $E\left( {A,~Z + 1} \right)$ используется внутренняя энергия $i$‑го состояния промежуточного ядра, $\left( {\Gamma _{{tot}}^{{{{{\left( {Z + 1} \right)}}_{i}}}}} \right)$ – полная ширина распада указанного состояния $i$, а ${{T}_{1}}$ – суммарная кинетическая энергия двух вылетающих при $\beta _{1}^{ - }$-распаде родительского ядра легких частиц, определяемая формулой (4). При использовании амплитуды ширины $2{{\beta }^{ - }}$-распада родительского ядра $\left( {A,Z} \right)$, представленной диаграммой Фейнмана (см. рис. 1), указанную ширину $\Gamma _{{2\beta }}^{Z}$ на основе методов, развитых в работах [8–10] для 2p-распада ядер, можно представить как: где $\Gamma _{{\beta _{1}^{ - }{{{\left( {Z + 1} \right)}}_{i}}}}^{Z}\left( {{{T}_{1}}} \right)$ и $\Gamma _{{\beta _{2}^{ - }\left( {Z + 2} \right)}}^{{{{{\left( {Z + 1} \right)}}_{i}}}}\left( {{{Q}_{{2{{\beta }^{ - }}}}} - {{T}_{1}}} \right)$ – парциальные ширины $\beta _{1}^{ - }$ и $\beta _{2}^{ - }$-распадов родительского и промежуточного ядер. Теперь, как и в случае теории 2p-распадов [8–10], можно выделить два типа рассматриваемых последовательных двухступенчатых $2{{\beta }^{ - }}$-распадов ядер: первого связанного с последовательными, реализующимися через два последовательных реальных ${\beta }$-распада родительского и возникающего из него промежуточного ядра и второй тип виртуальными распадами, получившее свое название по аналогии с 2p-распадом, когда все $i$-е состояния промежуточного ядра функции Грина носят виртуальный характер, поскольку лежат вне массовой поверхности.

2. ВИРТУАЛЬНОСТЬ $2\beta $-РАСПАДОВ ЯДЕР

Второй тип $2{{{\beta }}^{ - }}$-распадов возникает в случае, когда теплота ${{Q}_{{{\beta }_{1}^{ - }}}}$ для $\beta _{1}^{ - }$-распада родительского ядра имеет отрицательное значение ${{Q}_{{\beta _{1}^{ - }}}} < 0$, что приводит к невозможности появления реального ${\beta }_{1}^{ - }$-распада. В этом случае при теплоте ${{Q}_{{{\beta }_{2}^{ - }}}}$ для ${\beta }_{2}^{ - }$-распада промежуточного ядра, удовлетворяющей условию ${{Q}_{{\beta _{2}^{ - }}}} > \left| {{{Q}_{{\beta _{1}^{ - }}}}} \right|$, теплота ${{Q}_{{2{{{\beta }}^{ - }}}}}$ для $2{{{\beta }}^{ - }}$-распада, равная ${{Q}_{{2{{\beta }^{ - }}}}} = {{Q}_{{\beta _{1}^{ - }}}} + {{Q}_{{\beta _{2}^{ - }}}}$, оказывается положительной ${{Q}_{{2{{{\beta }}^{ - }}}}} > 0$, что обеспечивает возможность реального $2{{\beta }^{ - }}$-распада родительского ядра.

Полученные выше энергетические условия виртуальности $2{{\beta }^{ - }}$-распадов четно-четных родительских ядер реализуются [11, 12], как и для 2p‑распадов подобных ядер, из-за куперовского спаривания нуклонов. Действительно, в этом случае из-за отрицательности энергии спаривания двух валентных нейтронов в родительском ядре, образующих куперовскую пару, уменьшается теплота ${{Q}_{{{\beta }_{1}^{ - }}}}$, связанная с первым ${\beta }_{1}^{ - }$-распадом и образованием нечетного по нейтронам промежуточного ядра, по сравнению с теплотой ${{Q}_{{{\beta }_{2}^{ - }}}}$ второго ${\beta }_{2}^{ - }$-распада нейтрона в промежуточном ядре, который не участвует в формировании куперовской пары. Исходя из этого варианта функция Грина $G\left( {A,Z + 1} \right)$ промежуточного ядра (15) не имеет полюсного характера, и тогда можно записать формулу для ширины виртуального (virtual) двойного ${{{\beta }}^{ - }}$-распада ядра $\left( {A,~Z} \right)$:

Существующие расчеты периодов полураспада $T_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{th}}$ для $2{{\beta }^{ - }}$-распадов ядер основаны на теоретических подходах [6], в которых используются формулы второго порядка теории возмущений по гамильтонианам слабого взаимодействия. Эти формулы оказываются близкими к формулам, используемым в настоящей работе для виртуального варианта теории описания $2{{\beta }^{ - }}$-распадов ядер (17), но, к сожалению, не учитывают при расчете анализируемых ширин роль однонуклонных генеалогических коэффициентов сверхтекучей модели атомного ядра [13], учет которых может дать поправку примерно на порядок.

В табл. 1–3, взятых из работ [2, 3, 14–18], представлены экспериментальные данные и результаты расчетов для $2{{\beta }^{ - }}$; $2{{\beta }^{ + }}$; ${{\beta }^{ + }},~EC$ и $EC,EC$ распадов. Как видно из табл. 1, для всех представленных в ней четно-четных родительских ядер теплоты $2{{\beta }^{ - }}$-распада ${{Q}_{{2{{\beta }^{ - }}}}}$, как и следовало ожидать для возможности их наблюдения, имеют положительные значения, лежащие в интервале $0.850 \leqslant {{Q}_{{2{{\beta }^{ - }}}}} \leqslant 4.280~\,\,\left( {{\text{МэВ}}} \right)$. При этом теплоты ${\beta }_{1}^{ - }$-распадов ${{Q}_{{{\beta }_{1}^{ - }}}}$ большинства представленных в табл. 1 родительских ядер $\left( {A,Z} \right)$ лежат в интервале $ - 1.265 \leqslant {{Q}_{{\beta _{1}^{ - }}}} \leqslant - 0.055~\,\,\left( {{\text{МэВ}}} \right)$ и оказываются отрицательными, что соответствует закрытым каналам ${\beta }_{1}^{ - }$-распадов указанных ядер. Как видно из табл. 1, большинство ядер имеют значения экспериментальных $T_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{exp}}$ и теоретических $T_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{th}}$ периодов полураспада, достаточно хорошо согласующиеся между собой, за исключением ядер ¹¹⁰Pd, ¹⁴⁸Nd и ¹⁵⁴Sm, в которых наблюдаемые расхождения составляют несколько порядков, что связано, по-видимому, с существенными неточностями в определении экспериментальных значений $T_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{exp}}$ в этих ядрах.

Как видно из табл. 2, для всех представленных в ней четно-четных родительских ядер теплоты их $2{{\beta }^{ + }}$-распада ${{Q}_{{2{{{\beta }}^{ + }}}}}$ имеют положительные значения, лежащие в интервале $0.820 \leqslant {{Q}_{{2{{\beta }^{ + }}}}} \leqslant 3.200\,\,~\left( {{\text{МэВ}}} \right)$, что делает открытыми указанные распады, а теплоты ${{Q}_{{\beta _{1}^{ + }}}}$ для $\beta _{1}^{ + }$-распадов указанных ядер оказываются отрицательными и лежащими в интервале $ - 1.300 \leqslant {{Q}_{{\beta _{1}^{ + }}}} \leqslant - 0.036~\,\,\left( {{\text{МэВ}}} \right)$, что соответствует закрытым каналам ${\beta }_{1}^{ + }$-распадов указанных ядер. К сожалению, представленные в табл. 2 экспериментальные периоды полураспада $T_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{exp}}$, представленные их нижними границами, расходятся более, чем на 7 порядка с соответствующими теоретическими периодами полураспада $T_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{{th}}$, что приводит к необходимости проведения более точных экспериментов по всем рассмотренным ядрам.

Наконец, как видно из табл. 3, где представлены теоретические и экспериментальные периоды полураспада для ${{\beta }^{ + }},EC$ и $EC,EC$ распадов, для большинства родительских ядер имеются серьезные расхождения между указанными величинами и лишь для единственного ядра ¹³⁰Ba, при $EC,EC$ распаде наблюдается хорошее согласие между ними.

В заключение следует отметить, что многочисленные попытки наблюдения безнейтринных $2\beta $-распадов различных ядер со схемами распадов, отличающимися от схем двухнейтринных $2\beta $-распадов, представленных формулами типа (7), отсутствием нейтрино и антинейтрино, не привели к убедительным результатам. Поскольку наблюдение безнейтринных $2{\beta }$-распадов ядер может дать важную информацию о качественных свойствах нейтрино, подобные эксперименты продолжаются различными группами физиков до сих пор.

3. $2{\beta }$-РАСПАДЫ ЯДЕР КАК ПОСЛЕДОВАТЕЛЬНЫЕ РЕАЛЬНЫЕ ${\beta }$-РАСПАДЫ РОДИТЕЛЬСКОГО И ПРОМЕЖУТОЧНОГО ЯДРА

Если рассмотреть случай, когда обе теплоты ${{Q}_{{{\beta }_{1}^{ - }}}}{\text{\;}}$ и ${{Q}_{{\beta _{2}^{ - }}}}$ положительны, то полную ширину $2{{\beta }^{ - }}$-распада родительского ядра можно записать в виде суммы ширин последовательного и виртуального $2{{\beta }^{ - }}$-распада:

Первый тип реализуется в случае двух последовательных реальных ${{\beta }^{ - }}$-распадов родительского и промежуточного ядер с положительными теплотами распадов ${{Q}_{{\beta _{1}^{ - }}}} > 0$ и ${{Q}_{{\beta _{2}^{ - }}}} > 0$. Тогда в подынтегральном выражении формулы (16) возникает полюс в комплексной плоскости при ${{T}_{1}} = {{Q}_{{{{\beta }_{1}}i}}} + \frac{1}{2}\left( {\Gamma _{{tot}}^{{{{{\left( {Z + 1} \right)}}_{i}}}}} \right),$ так что интегрирование по $d{{T}_{1}}$ с учетом теоремы Коши приводит к формуле:

определяющую ширину ${{(\Gamma _{{2{{\beta }^{ - }}}}^{Z})}^{0}}$ для $2{{{\beta }}^{ - }}$-распада родительского ядра, осуществляемого через два последовательных реальных ${{{\beta }}^{ - }}$-распадов. Если провести анализ формулы (19), то можно увидеть, что если после первого ${\beta }_{1}^{ - }$-распада из возможных каналов распада промежуточного ядра реализуется только ${{{\beta }}^{ - }}$-распадный, то ширина второго ${\beta }_{2}^{ - }$-распада равна полной ширине распада промежуточного ядра $\Gamma _{{\beta _{2}^{ - }\left( {Z + 2} \right)}}^{{{{{\left( {Z + 1} \right)}}_{i}}}}\left( {{{Q}_{{2{{\beta }^{ - }}}}} - {{T}_{1}}} \right) = \Gamma _{{tot}}^{{{{{\left( {Z + 1} \right)}}_{i}}}}$. Исходя из этого, формула (18) принимает вид:

Лишь только для двух родительских ядер ⁴⁸Ca₂₀ и ⁹⁶Zr₄₀, представленных в табл. 1, энергии ${{Q}_{{\beta _{1}^{ - }}}}$ оказываются положительными, что делает открытыми не только канал $2{{{\beta }}^{ - }}$-распада, но и канал ${{{\beta }}^{ - }}$-распада указанных ядер. Из формулы (20) следует, что в случае, когда у нас ${{Q}_{{\beta _{1}^{ - }}}} > 0$, ${{Q}_{{\beta _{2}^{ - }}}} > 0$, то есть возможность протекания двух следующих друг за другом по времени реальных бета-распадов, а ширина $2{{\beta }^{ - }}$-распада определяется шириной первого ${{\beta }^{ - }}$-распада. Это означает, что данный вариант последовательного двухступенчатого $2{{\beta }^{ - }}$-распада не мог быть учтен в более ранних теоретических работах [2, 3, 6], основанных на втором порядке теории возмущения по гамильтониану слабого взаимодействия. В то же время для двух родительских ядер ⁴⁸Ca и ⁹⁶Zr экспериментально зафиксирован такой распад с участием реальных $\beta _{1}^{ - }$- и $\beta _{2}^{ - }$-распадов родительского и промежуточного ядер с вероятностью ${{10}^{{ - 2}}}$ от вероятности виртуального $2{{{\beta }}^{ - }}$-распада указанных ядер. Для этих ядер в табл. 4 представлены теоретические и экспериментальные ширины ${{{\beta }}^{ - }}$-распадов, из которых видно хорошее согласие между $\Gamma _{{2\beta }}^{{exp}}$ и ${\Gamma }_{{2{\beta }}}^{{th}}$, рассчитанных в рамках данного типа теории последовательного $2{{{\beta }}^{ - }}$-распада.

Представляется интересным провести анализ случая, когда теплота первого ${{{\beta }}^{ - }}$-распада положительны ${{Q}_{{\beta _{1}^{ - }}}} > 0$, но мала по своему абсолютному значению, тогда возникает случай, когда полная ширина $2{{{\beta }}^{ - }}$-распада определяется суммой виртуального и последовательного типов, причем вклады от двух типов могут быть соизмеримы, что легко видно из формулы для полной ширины (18).

ЗАКЛЮЧЕНИЕ

Проведено дальнейшее развитие теории 2${\beta }$‑распадов ядер при использовании результатов, полученных при построении теории двухпротонных распадов ядер [8–10]. Установлено существование двух типов рассматриваемых распадов. Первый тип отвечает $2\beta $-распадам, которые реализуются через два последовательных реальных ${\beta }$-распада родительского и возникающего из него промежуточного ядра. Второй тип связан с виртуальным характером относящихся к нему $2{\beta }$‑распадов, ширины которых описываются формулами, аналогичными формулам, полученным ранее во втором порядке теории возмущений по гамильтониану слабого взаимодействия. Продемонстрирована возможность успешного описания экспериментальных характеристик $2{\beta }$-распада ядер для большинства родительских ядер в рамках виртуального типа, а также двух родительских ядер ⁴⁸Ca и ⁹⁶Zr, распад которых экспериментально зафиксирован и протекает с участием реальных ${\beta }_{1}^{ - }$- и ${\beta }_{2}^{ - }$-распадов родительского и промежуточного ядер, а ширины указанных распадов с хорошей степенью точности определяются последовательным типом.