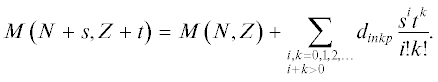Известия РАН. Серия физическая, 2020, T. 84, № 10, стр. 1395-1400
Полиномиальное описание масс нечетных деформированных ядер
А. К. Власников 1, *, А. И. Зиппа 1, В. М. Михайлов 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Санкт-Петербургский государственный университет”
Санкт-Петербург, Россия
* E-mail: a.vlasnikov@spbu.ru
Поступила в редакцию 11.05.2020
После доработки 02.06.2020
Принята к публикации 26.06.2020
Аннотация
Рассмотрено описание масс нечетных деформированных атомных ядер с помощью полиномов четвертого порядков по отклонениям от N и Z нечетного ядра. Показано, что переход от второго порядка к четвертому не сближает параметры, полученные для разных групп четно-четных ядер, при этом параметры высших порядков, вычисленные таким же образом, не удовлетворительно согласуются друг с другом. “Гладкая” составляющая массы нечетного ядра практически одинакова для четвертого и второго порядков. На этой основе делается заключение, что вполне достаточно ограничиться полиномом второго порядка.
ВВЕДЕНИЕ
Одной из актуальных проблем структуры атомного ядра является вопрос о парных корреляциях и их влиянии на свойства атомных ядер. Сжатие энергетических уровней в нечетных и нечетно-нечетных ядрах по сравнению с одночастичным спектром, появление энергетической щели в неротационных спектрах четно-четных ядер, уменьшение момента инерции в ротационных спектрах деформированных ядер – далеко не полный список проявлений парных корреляций. Количественной мерой парных корреляций являются нейтронные (n) и протонные (p) парные энергии Pτ (τ = n, p), определяемые как превышение массы нечетного ядра над соседними четно-четными. Если определить некоторую гладкую функцию $\mathcal{M}\left( {N,Z} \right)$, описывающую зависимость массы четно-четных ядер от количества нейтронов N и количества протонов Z, то массу нечетно-нейтронного ядра $M\left( {{{N}_{{\text{н}}}},Z} \right)$ или массу нечетно-протонного ядра $M\left( {N,{{Z}_{{\text{н}}}}} \right)$ можно определить через гладкую составляющую компоненту массы $\mathcal{M}\left( {N,Z} \right)$ и парные энергии Pτ (τ = n, p):
(1)
$M\left( {{{N}_{{\text{н}}}},Z} \right) = \mathcal{M}\left( {{{N}_{{\text{н}}}},Z} \right) + {{P}_{n}}\left( {{{N}_{{\text{н}}}},Z} \right),$(2)
$M\left( {N,{{Z}_{{\text{н}}}}} \right) = \mathcal{M}\left( {N,{{Z}_{{\text{н}}}}} \right) + {{P}_{p}}\left( {N,{{Z}_{{\text{н}}}}} \right),$Из формул (1) и (2) следует, что однозначность вычисления Pτ зависит от однозначности выделения “гладкой” массы $\mathcal{M}\left( {N,Z} \right)$ и ее аналитической зависимости от N и Z. Поскольку Pτ в основном определяются парными корреляциями в ядрах, то вычисленные на основе формул (1) и (2) парные энергии могут послужить для уточнения выбора эффективных взаимодействий в частично-частичном канале. Для этой цели парные энергии используются в течение долгого времени, см. например, [2–4].
Существует много способов расчета Pτ (τ = n, p) на основе ядерных масс. Ниже для краткости рассмотрены только нейтронные парные энергии Pn. Для протонных парных энергий Pp используются те же формулы с заменой N на Z (и перестановкой: нейтронные числа должны быть первыми). Обычно вычисляют нейтронные парные энергии с массами ядер при фиксированном четном Z, как, например, в определении Бора и Моттельсона [5]:
(3)
$\begin{gathered} {{P}_{n}} = \left[ {3M\left( {N - 1,Z} \right) + M\left( {N + 1,Z} \right)} \right. - \\ {{\left. { - \,\,M\left( {N - 2,Z} \right) - 3M\left( {N,Z} \right)} \right]} \mathord{\left/ {\vphantom {{\left. { - \,\,M\left( {N - 2,Z} \right) - 3M\left( {N,Z} \right)} \right]} 4}} \right. \kern-0em} 4}, \\ \end{gathered} $здесь и в (4) N и Z – четные числа. Более симметричное выражение предложено Мадландом и Никсом [6]:
(4)
$\begin{gathered} {{P}_{n}} = \left[ {4M\left( {N - 1,Z} \right) + 4M\left( {N + 1,Z} \right)} \right. - \\ {{\left. { - \,\,M\left( {N + 2,Z} \right) - M\left( {N - 2,Z} \right) - 6M\left( {N,Z} \right)} \right]} \mathord{\left/ {\vphantom {{\left. { - \,\,M\left( {N + 2,Z} \right) - M\left( {N - 2,Z} \right) - 6M\left( {N,Z} \right)} \right]} 8}} \right. \kern-0em} 8}. \\ \end{gathered} $В оба этих определения парной нейтронной энергии, как в (3), так и в (4), входят две массы нечетного ядра $M\left( {N + 1,Z} \right)$ и $M\left( {N - 1,Z} \right),$ то есть дается некоторое среднее от Pn для двух нечетных ядер. На это было обращено внимание в [7], где было предложено уравнение, содержащее одну массу нечетного ядра
(5)
$\begin{gathered} {{P}_{n}} = M({{N}_{{\text{н}}}},Z) - \{ 9[M({{N}_{{\text{н}}}} + 1,Z) + M({{N}_{{\text{н}}}} - 1,Z)] - \\ - \,\,[M({{N}_{{\text{н}}}} + 3,Z) + {{M({{N}_{{\text{н}}}} - 3,Z)]\} } \mathord{\left/ {\vphantom {{M({{N}_{{\text{н}}}} - 3,Z)]\} } {16}}} \right. \kern-0em} {16}} \\ \end{gathered} $(Nн – нечетное, Z – четное, как и в (1)), что позволяет фиксировать квантовое состояние нечетного нуклона. Уравнение (5) является обобщением довольно старого определения парной энергии, которое до сих пор используется при отсутствии достаточного числа соседних масс четно-четных ядер:
(6)
$\begin{gathered} {{P}_{n}} = M({{N}_{{\text{н}}}},Z) - \\ - \,\,[M({{N}_{{\text{н}}}} + 1,Z) + {{M({{N}_{{\text{н}}}} - 1,Z)]} \mathord{\left/ {\vphantom {{M({{N}_{{\text{н}}}} - 1,Z)]} 2}} \right. \kern-0em} 2}. \\ \end{gathered} $Как выяснилось в [7], при использовании уравнения (5) нечетные ядра, например, нечетно-нейтронные с Nн и Nн + 2 могут иметь парные энергии Pn(Nн, Z) и Pn(Nн + 2, Z), которые отличаются на ∼100 кэВ и более.
Как уже отмечалось в [1], в основе выражений (3)‒(5) лежит предположение о гладкости изменения масс четно-четных ядер, которая в нечетных ядрах нарушается из-за парных энергий Pτ. Тогда (см. [6]) для четно‑четного ядра с количеством нейтронов N + s и протонов Z + t (s, t малы: $\left| {{s \mathord{\left/ {\vphantom {s N}} \right. \kern-0em} N}} \right| < 1$ и $\left| {{t \mathord{\left/ {\vphantom {t Z}} \right. \kern-0em} Z}} \right| < 1$) можно написать:
Формально этот ряд подобен ряду Тейлора, но параметры dinkp не являются производными, хотя они так называются, например, в [5] и [6], так как s и t принимают дискретные значения. Если разлагать по s и t энергию ядра
(8)
$\left. \begin{gathered} M(N,Z) = {{m}_{n}}N + {{m}_{p}}Z + E(N,Z) \\ E(N,Z) = - B(N,Z) \\ \end{gathered} \right\}$(mn, mp – массы нуклонов, B – энергия связи), то все параметры за исключением d1n0p, d0n1p и M(N, Z) не изменяются. При разложении E(N + s, Z + t) масса M(N, Z) заменяется на E(N, Z), а d1n0p на ${{\bar {d}}_{{1n0p}}}$ и d0n1p на ${{\bar {d}}_{{0n1p}}}$
(9)
${{\bar {d}}_{{1n0p}}} = - {{m}_{n}} + {{d}_{{1n0p}}};\,\,{{\bar {d}}_{{0n1p}}} = - {{m}_{p}} + {{d}_{{0n1p}}}.$Обозначим din0p ≡ din; d0nkp ≡ dkp. Величины ${{d}_{{inkp}}}$ назовем параметрами первого порядка, если i + k = = 1, второго порядка, если i + k = 2, третьего порядка, если i + k = 3 и т.д.; четно-четными, если i = 2μ, k = 2ν, нечетно-нечетными, если i = 2μ + 1, k = 2ν + 1.
Если исходить из того, что единственный источник негладкости в поведении масс нечетных атомных ядер – парные энергии, то, следуя логике разложения (7), можно выразить массу четно-четного ядра через “гладкую” массу $\mathcal{M}$ нечетного ядра. Тогда при нечетном s:
(10)
$M\left( {{{N}_{{\text{н}}}} + s,Z} \right) = \mathcal{M}\left( {{{N}_{{\text{н}}}},Z} \right) + s{{d}_{{1n}}}\left( {{{N}_{n}},Z} \right) + \ldots .$Естественно, что параметры ${{d}_{{inkp}}}$ в выражении (7) можно рассчитать, используя разные группы ядер, соседних с N и Z. Разложение (7) можно считать применимым, если параметры мало меняются от группы к группе. Кроме того, ряд (7) в общем случае бесконечен, и возникает вопрос об оптимальном количестве членов.
Подобное исследование было проведено для четно-четных ядер в [8], где массовая поверхность аппроксимировалась на основе уравнения (7), включающего параметры вплоть до второго, затем до четвертого и, наконец, вплоть до шестого порядка. Исследовались массовые поверхности, в центре которых были два полумагических ядра с A = 118, N = 68, Z = 50 и с A = 140, N = 82, Z = 58 и одно деформированное ядро А = 170, N = = 100, Z = 70. Результаты [8] показывают, что dkn, dkp при k = 3, 4 имеют близкий порядок величины, хотя различие этих параметров, определенных по разным группам ядер, может быть сравнимо с величиной параметров. В то же время параметры dinkp, i ≠ 0, k ≠ 0, существенно различаются при определении по разным группам ядер, за исключением d1n1p. Общий вывод состоит в том, что для четно-четных ядер наилучший результат дает аппроксимация с параметрами не выше второго порядка, хотя поправки к d1n, d1p за счет третьего порядка и к d2n, d2p за счет четвертого порядка приводят к сближению этих параметров для разных групп ядер.
В работе [1] изучена массовая поверхность стабильных деформированных ядер с нечетным количеством нейтронов ${}_{{64}}^{{157}}{\text{Gd,}}{}_{{70}}^{{171}}{\text{Yb,}}{}_{{72}}^{{179}}{\text{Hf}}$ и с нечетным количеством протонов ${}_{{67}}^{{165}}{\text{Ho,}}{}_{{71}}^{{175}}{\text{Lu}}$. “Гладкая” часть $\mathcal{M}\left( {N,Z} \right)$ представлена как полином второго порядка по отклонениям от N и Z. Параметры разложения были определены на основании двух различных групп соседних ядер. В первой группе ядер к нечетному нуклону нечетного ядра добавлялись или отделялись 1 и 3 нуклона (в работе [1] обозначено как приближение А (А)). Во второй группе ядер к четному нуклону нечетного ядра добавлялись или отделялись 2 или 4 нуклона, а к нечетному – 1 или 3 нуклона (в работе [1] обозначено как приближение Б (Б)). Таким образом, в обоих случаях расчеты проводились по массам соседних четно-четных ядер. Результаты [1] показывают, что параметры ${{\bar {d}}_{{1\tau }}}$ и ${{\bar {d}}_{{2\tau }}}$, определенные для разных групп ядер, отличаются незначительно. При этом остается открытым вопрос, сближаются ли значения этих параметров при переходе к описанию массовой поверхности полиномами 4 порядка.
В настоящей статье рассмотрено описание массовой поверхность нечетных ядер полиномами вплоть до 4 порядка. Выбор двух различных групп ядер, на основе которых производился расчет параметров, аналогичен работе [1], однако, поскольку количество неизвестных параметров увеличено, увеличено и количество нуклонов в каждой из групп. В первую группу добавлены ядра, в которых количество нуклонов отличается на пять от количества нечетных нуклонов в рассматриваемом ядре. Во вторую группу по сравнению с работой [1] добавлены ядра, в которых к четному нуклону добавлены или удалены еще шесть нуклонов, а к нечетному – пять. Формулы, на основе которых проводились вычисления, приведены во втором разделе. Третий раздел посвящен результатам расчетов и их анализу.
ПАРАМЕТРЫ МАССОВОЙ ПОВЕРХНОСТИ ЧЕТВЕРТОГО ПОРЯДКА
Расчет параметров “гладкой” составляющей массовой поверхности нечетных атомных ядер в окрестностях заданных Z и N производится на основе двух совокупностей атомных ядер. При этом в настоящей работе учтены параметры вплоть до четвертого.
В первой совокупности сохраняется неизменным четное количество нуклонов, а нечетное количество нуклонов изменяется на (±1, ±3, ±5). Таким образом, расчет 5 параметров $\mathcal{M}$, d1τ, d2τ, d3τ, d4τ для нечетного ядра ведется на основе масс соседних четно-четных ядер. Найденные таким способом параметры обозначим приближением а (a).
Во второй совокупности количество четных нуклонов изменяется на ±2, ±4, ±6 единиц, а количество нечетных – на ±1, ±3, ±5 единиц. В этом приближении можно найти все 15 параметров, начиная от $\mathcal{M}$, d1n, d1p, d2n, d2p, d1n1p вплоть до параметров четвертого порядка (d4n, d4p, d3n1p, d1n3p, d2n2p). Найденные таким способом параметры обозначим приближением б (б).
Как показано в [1, 8], расчет искомых параметров удобно производить, используя суммы e(s, t) и разности o(s, t) масс ядер в окрестностях изучаемого нечетного ядра. При использовании параметров вплоть до третьего и четвертого порядка:
(11)
$\begin{gathered} e\left( {s,t} \right) = \mu \left( {N + s,Z + t} \right) + \mu \left( {N - s,Z - t} \right) = \\ = 2\mu \left( {N,Z} \right) + {{s}^{2}}{{d}_{{2n}}} + {{t}^{2}}{{d}_{{2p}}} + 2st{{d}_{{1n1p}}} + \\ + \,\,\frac{{2{{s}^{4}}}}{{4{\text{!}}}}{{d}_{{4n}}} + \frac{{2{{t}^{4}}}}{{4{\text{!}}}}{{d}_{{4p}}} + \frac{{{{s}^{3}}t}}{3}{{d}_{{3n1p}}} + \frac{{s{{t}^{3}}}}{3}{{d}_{{1n3p}}} + \frac{{{{s}^{2}}{{t}^{2}}}}{2}{{d}_{{2n2p}}}; \\ \end{gathered} $(12)
$\begin{gathered} o\left( {s,t} \right) = \mu \left( {N + s,Z + t} \right) - \mu \left( {N - s,Z - t} \right) = \\ = 2s{{d}_{{1n}}} + 2t{{d}_{{1p}}} + \frac{{{{s}^{3}}}}{3}{{d}_{{3n}}} + \frac{{{{t}^{3}}}}{3}{{d}_{{3p}}} + \\ + \,\,{{s}^{2}}t{{d}_{{2n1p}}} + s{{t}^{2}}{{d}_{{1n2p}}}, \\ \end{gathered} $Если ядра четные (нечетные), то μ = M (μ = $\mathcal{M}$), s и t принимают целочисленные значения, d0n0p = = M(N, Z) (d0n0p = $\mathcal{M}$(N,Z)).
Комбинация масс ee(s, t) содержит только четно-четные параметры.
(13)
$\begin{gathered} ee(s,t) = e(s, - t) + e(s,t) = \\ = \,\,4M(N,Z) + 2{{s}^{2}}{{d}_{{2n}}} + 2{{t}^{2}}{{d}_{{2p}}} + \\ + \,\,\frac{{{{s}^{4}}}}{6}{{d}_{{4n}}} + \frac{{{{t}^{4}}}}{6}{{d}_{{4p}}} + {{s}^{2}}{{t}^{2}}{{d}_{{2n2p}}}. \\ \end{gathered} $Разности ee(s, t) могут быть использованы для выделения параметров четных по нейтронам или по протонам:
(14)
$\begin{gathered} e{{e}_{n}}({{s}_{1}},{{s}_{2}}\left| t \right.) = ee({{s}_{1}},t) - ee({{s}_{2}},t) = \\ = \,\,2(s_{1}^{2} - s_{2}^{2}){{d}_{{2n}}} + {{(s_{1}^{4} - s_{2}^{4}){{d}_{{4n}}}} \mathord{\left/ {\vphantom {{(s_{1}^{4} - s_{2}^{4}){{d}_{{4n}}}} 6}} \right. \kern-0em} 6} + (s_{1}^{2} - s_{2}^{2}){{t}^{2}}{{d}_{{2n2p}}}, \\ \end{gathered} $(15)
$\begin{gathered} e{{e}_{p}}(\left. s \right|{{t}_{1}},{{t}_{2}}) = ee(s,{{t}_{1}}) - ee(s,{{t}_{2}}) = \\ = \,\,2(t_{1}^{2} - t_{2}^{2}){{d}_{{2p}}} + {{(t_{1}^{4} - t_{2}^{4}){{d}_{{4p}}}} \mathord{\left/ {\vphantom {{(t_{1}^{4} - t_{2}^{4}){{d}_{{4p}}}} 6}} \right. \kern-0em} 6} + (t_{1}^{2} - t_{2}^{2}){{s}^{2}}{{d}_{{2n2p}}}. \\ \end{gathered} $Комбинация масс ядер Sτ(s, t) выделяет нечетно-нейтронные (τ = n), либо нечетно-протонные (τ = p) параметры:
(16)
$\begin{gathered} {{S}_{n}}(s,t) = o(s, - t) + o(s,t) = \\ = \,\,4s{{d}_{{1n}}} + {{2{{s}^{3}}{{d}_{{3n}}}} \mathord{\left/ {\vphantom {{2{{s}^{3}}{{d}_{{3n}}}} 3}} \right. \kern-0em} 3} + 2s{{t}^{2}}{{d}_{{1n2p}}}, \\ \end{gathered} $(17)
$\begin{gathered} {{S}_{p}}(s,t) = o( - s,t) + o(s,t) = \\ = \,\,4t{{d}_{{1p}}} + {{2{{t}^{3}}{{d}_{{3p}}}} \mathord{\left/ {\vphantom {{2{{t}^{3}}{{d}_{{3p}}}} 3}} \right. \kern-0em} 3} + 2{{s}^{2}}t{{d}_{{2n1p}}}. \\ \end{gathered} $Используя выражения (11)‒(17), можно получить искомые параметры.
(а): s = ±1, ±3, ±5; t = 0; ΔA = 1; 3; 5.
(19)
${{d}_{{2n}}} = {{2}^{{ - 6}}}\left[ {13e(3,0) - \frac{{34}}{3}e(1,0) - \frac{5}{3}e(5,0)} \right],$Т.к. число использованных масс в (а) равно 6, а параметров только 5, то появляется возможность вычислить 2 варианта d1n и d3n: один вариант с ΔA = 1, 3, второй – ΔA = 3, 5:
(21)
${{d}_{{1n}}}(\Delta A = 1;3) = {{9o(1,0)} \mathord{\left/ {\vphantom {{9o(1,0)} {16 - {{o(3,0)} \mathord{\left/ {\vphantom {{o(3,0)} {48}}} \right. \kern-0em} {48}}}}} \right. \kern-0em} {16 - {{o(3,0)} \mathord{\left/ {\vphantom {{o(3,0)} {48}}} \right. \kern-0em} {48}}}};$(22)
${{d}_{{3n}}}(\Delta A = 1;3) = {{[o(3,0) - 3o(1,0)]} \mathord{\left/ {\vphantom {{[o(3,0) - 3o(1,0)]} 8}} \right. \kern-0em} 8};$(23)
${{d}_{{1n}}}(\Delta A = 3;5) = {{25o(3,0)} \mathord{\left/ {\vphantom {{25o(3,0)} {96 - {{9o(5,0)} \mathord{\left/ {\vphantom {{9o(5,0)} {160;}}} \right. \kern-0em} {160;}}}}} \right. \kern-0em} {96 - {{9o(5,0)} \mathord{\left/ {\vphantom {{9o(5,0)} {160;}}} \right. \kern-0em} {160;}}}}$(24)
${{d}_{{3n}}}(\Delta A = 3;5) = {{3o(5,0)} \mathord{\left/ {\vphantom {{3o(5,0)} {80 - {{o(3,0)} \mathord{\left/ {\vphantom {{o(3,0)} {16}}} \right. \kern-0em} {16}}}}} \right. \kern-0em} {80 - {{o(3,0)} \mathord{\left/ {\vphantom {{o(3,0)} {16}}} \right. \kern-0em} {16}}}}.$(б): ниже даны выражения для нейтронных параметров, которые можно сравнить с нейтронными параметрами (18)‒(24) для (а). s = ±1, ±3, ±5; t = ±2, ±4, ±6; ΔA = |s + t| = 1, 3, 5, 7.
Чтобы не вычислять в (б) параметры dinkp, i ≠ k, i и k ≠ 0, в частности, нечетно-нечетные используются een(s1, s2|t) и eep(s|t1, t2) (14), (15). В таком случае приходится использовать 24 массы ядер, в то время как имеется всего 15 параметров. Из этого следует, что для d1n и d3n даются 2 варианта: один, который обозначен как (I), содержит массы с ΔA = 1, 3, 5, и второй, обозначенный как (II), использует массы с ΔA = 1, 3, 5, 7.
(25)
$\begin{gathered} \mathcal{M}\left( {{{N}_{{\text{н}}}},Z} \right) = \frac{1}{4}e\left( {1,2} \right) - \frac{{91}}{3}{{2}^{{ - 9}}}e{{e}_{n}}\left( {3,1\left| 2 \right.} \right) + \\ + \,\,\frac{1}{{96}}e{{e}_{n}}\left( {3,1\left| 4 \right.} \right) + 3 \cdot {{2}^{{ - 9}}}e{{e}_{n}}\left( {5,1\left| 2 \right.} \right) - \\ - \,\,\frac{3}{{20}}e{{e}_{p}}(\left. 1 \right|4,2) + \frac{1}{{40}}e{{e}_{p}}(\left. 1 \right|6,2); \\ \end{gathered} $(26)
$\begin{gathered} {{d}_{{2n}}}({{N}_{n}},Z) = \\ = \,\,{{\left[ {\frac{{47}}{8}e{{e}_{n}}(3,\left. 1 \right|2) - e{{e}_{n}}(3,\left. 1 \right|4) - \frac{5}{8}e{{e}_{n}}(5,\left. 1 \right|2)} \right]} \mathord{\left/ {\vphantom {{\left[ {\frac{{47}}{8}e{{e}_{n}}(3,\left. 1 \right|2) - e{{e}_{n}}(3,\left. 1 \right|4) - \frac{5}{8}e{{e}_{n}}(5,\left. 1 \right|2)} \right]} {48}}} \right. \kern-0em} {48}}; \\ \end{gathered} $(27)
${{d}_{{4n}}}({{N}_{n}},Z) = {{[e{{e}_{n}}(5,\left. 1 \right|2) - 3e{{e}_{n}}(3,\left. 1 \right|2)]} \mathord{\left/ {\vphantom {{[e{{e}_{n}}(5,\left. 1 \right|2) - 3e{{e}_{n}}(3,\left. 1 \right|2)]} {64}}} \right. \kern-0em} {64}};$een(s1, s2|t) и eep(s|t1, t2) определены в (14), (15).
(28)
${{d}_{{1n}}}({\text{I}}) = {{35S(1,2)} \mathord{\left/ {\vphantom {{35S(1,2)} {96 - {{S(1,4)} \mathord{\left/ {\vphantom {{S(1,4)} {12}}} \right. \kern-0em} {12}} - {{S(3,2)} \mathord{\left/ {\vphantom {{S(3,2)} 9}} \right. \kern-0em} 9}}}} \right. \kern-0em} {96 - {{S(1,4)} \mathord{\left/ {\vphantom {{S(1,4)} {12}}} \right. \kern-0em} {12}} - {{S(3,2)} \mathord{\left/ {\vphantom {{S(3,2)} 9}} \right. \kern-0em} 9}}};$(29)
${{d}_{{3n}}}({\text{I}}) = {{S(3,2)} \mathord{\left/ {\vphantom {{S(3,2)} {16}}} \right. \kern-0em} {16}} - {{3S(1,2)} \mathord{\left/ {\vphantom {{3S(1,2)} {16}}} \right. \kern-0em} {16}}.$Функции S(s, t) определены в (16), (17).
(30)
${{d}_{{1n}}}({\text{II}}) = {{S(3,4)} \mathord{\left/ {\vphantom {{S(3,4)} 3}} \right. \kern-0em} 3} - {{11S(5,2)} \mathord{\left/ {\vphantom {{11S(5,2)} {160{{ - 13S(1,6)} \mathord{\left/ {\vphantom {{ - 13S(1,6)} {32}}} \right. \kern-0em} {32}}}}} \right. \kern-0em} {160{{ - 13S(1,6)} \mathord{\left/ {\vphantom {{ - 13S(1,6)} {32}}} \right. \kern-0em} {32}}}};$(31)
${{d}_{{3n}}}({\text{II}}) = {{ - S(3,4)} \mathord{\left/ {\vphantom {{ - S(3,4)} 4}} \right. \kern-0em} 4} + {{3S(5,2)} \mathord{\left/ {\vphantom {{3S(5,2)} {112 + {{9S(1,6)} \mathord{\left/ {\vphantom {{9S(1,6)} {812}}} \right. \kern-0em} {812}}.}}} \right. \kern-0em} {112 + {{9S(1,6)} \mathord{\left/ {\vphantom {{9S(1,6)} {812}}} \right. \kern-0em} {812}}.}}$РЕЗУЛЬТАТЫ РАСЧЕТОВ МАССОВОЙ ПОВЕРХНОСТИ ЧЕТВЕРТОГО ПОРЯДКА НЕЧЕТНЫХ ДЕФОРМИРОВАННЫХ ЯДЕР
Для расчета параметров $\mathcal{M}$ и dinkp применены формулы (18)‒(31). Так же, как в работе [1], изучены массовые поверхности стабильных нечетных деформированных ядер  ${}_{{64}}^{{157}}{\text{Gd}}$, ${}_{{67}}^{{165}}{\text{Ho,}}$ ${}_{{70}}^{{171}}{\text{Yb,}}$ ${}_{{71}}^{{175}}{\text{Lu и}}\,\,{}_{{72}}^{{179}}{\text{Hf}}$, в окрестностях которых много четно-четных ядер с измеренными массами. Экспериментальные
данные взяты из работы [9]. В табл. 1‒3 в первых трех колонках представлены массовое число A, заряд Z, τ = n для нечетно-нейтронных и τ = p для нечетно-протонных ядер. Рядом со значениями параметров в скобках – погрешности,
рассчитанные на основе эмпирических. Колонки “А [1]" и "Б [1]" приводят значения параметров, вычисленных в работе [1], где массовые поверхности тех же ядер описана полиномами второго порядка (см. введение
настоящей статьи). Два возможных набора параметров ${{\bar {d}}_{{1\tau }}}$ (ΔA = 1 и ΔA = 3) соответствуют двум различным группам ядер, на основе которых рассчитаны параметры.
Отметим, что для расчета параметров массовой поверхности четвертого порядка использовано
больше атомных ядер (ΔA ≤ 5 и 7), чем при расчете параметров поверхности второго порядка (ΔA ≤ 3). Парные энергии Pτ (табл. 3) приводятся только в A [1] для поверхности второго порядка и приближении (а) для поверхности четвертого порядка,
Pτ в оставшихся двух приближениях для поверхностей второго и четвертого порядков могут
быть получены с помощью разностей между известными массами нечетных ядер и рассчитанными
"гладкими” составляющими этих масс на основе формул (1) и (2). Например, нейтронная
парная энергия на основе массовой поверхности четвертого порядка в (а): Pn(а) = M(Nн, Z) – $\mathcal{M}$(а). Абсолютные значения M не приводятся, т.к. они имеют тот же порядок, что и массы соседних четно-четных ядер,
и могут быть легко восстановлены с использованием уравнений (1) и (2), значений Pτ и масс соответствующих нечетных ядер.
${}_{{64}}^{{157}}{\text{Gd}}$, ${}_{{67}}^{{165}}{\text{Ho,}}$ ${}_{{70}}^{{171}}{\text{Yb,}}$ ${}_{{71}}^{{175}}{\text{Lu и}}\,\,{}_{{72}}^{{179}}{\text{Hf}}$, в окрестностях которых много четно-четных ядер с измеренными массами. Экспериментальные
данные взяты из работы [9]. В табл. 1‒3 в первых трех колонках представлены массовое число A, заряд Z, τ = n для нечетно-нейтронных и τ = p для нечетно-протонных ядер. Рядом со значениями параметров в скобках – погрешности,
рассчитанные на основе эмпирических. Колонки “А [1]" и "Б [1]" приводят значения параметров, вычисленных в работе [1], где массовые поверхности тех же ядер описана полиномами второго порядка (см. введение
настоящей статьи). Два возможных набора параметров ${{\bar {d}}_{{1\tau }}}$ (ΔA = 1 и ΔA = 3) соответствуют двум различным группам ядер, на основе которых рассчитаны параметры.
Отметим, что для расчета параметров массовой поверхности четвертого порядка использовано
больше атомных ядер (ΔA ≤ 5 и 7), чем при расчете параметров поверхности второго порядка (ΔA ≤ 3). Парные энергии Pτ (табл. 3) приводятся только в A [1] для поверхности второго порядка и приближении (а) для поверхности четвертого порядка,
Pτ в оставшихся двух приближениях для поверхностей второго и четвертого порядков могут
быть получены с помощью разностей между известными массами нечетных ядер и рассчитанными
"гладкими” составляющими этих масс на основе формул (1) и (2). Например, нейтронная
парная энергия на основе массовой поверхности четвертого порядка в (а): Pn(а) = M(Nн, Z) – $\mathcal{M}$(а). Абсолютные значения M не приводятся, т.к. они имеют тот же порядок, что и массы соседних четно-четных ядер,
и могут быть легко восстановлены с использованием уравнений (1) и (2), значений Pτ и масс соответствующих нечетных ядер.
Таблица 1.
Нечетные параметры ${{\bar {d}}_{{1\tau }}},{{d}_{{3\tau }}}$ (кэВ). ${{\bar {d}}_{{1\tau }}} = {{d}_{{1\tau }}} - {{m}_{\tau }}$. В каждом приближении приведены два значения параметров, вычисленных с использованием масс четно-четных ядер с различными массовыми числами A. А [1], Б [1], (а), (б) – см. текст. Обозначения I и II объяснены в тексте перед уравнением (25)
| А [1] | Б [1] | (а) | (б) | (а) | (б) | |||
|---|---|---|---|---|---|---|---|---|
| A | Z | τ | $\begin{gathered} {{{\bar {d}}}_{{1\tau }}}\left( {\Delta A = 1} \right) \hfill \\ {{{\bar {d}}}_{{1\tau }}}\left( {\Delta A = 3} \right) \hfill \\ \end{gathered} $ | $\begin{gathered} {{{\bar {d}}}_{{1\tau }}}\left( {\Delta A = 1} \right) \hfill \\ {{{\bar {d}}}_{{1\tau }}}\left( {\Delta A = 3} \right) \hfill \\ \end{gathered} $ | $\begin{gathered} {{{\bar {d}}}_{{1\tau }}}\left( {\Delta A = 1;3} \right) \hfill \\ {{{\bar {d}}}_{{1\tau }}}\left( {\Delta A = 3;5} \right) \hfill \\ \end{gathered} $ | $\begin{gathered} {{{\bar {d}}}_{{1\tau }}}\left( {\text{I}} \right) \hfill \\ {{{\bar {d}}}_{{1\tau }}}\left( {{\text{II}}} \right) \hfill \\ \end{gathered} $ | $\begin{gathered} {{{\bar {d}}}_{{3\tau }}}\left( {\Delta A = 1;3} \right) \hfill \\ {{{\bar {d}}}_{{3\tau }}}\left( {\Delta A = 3;5} \right) \hfill \\ \end{gathered} $ | $\begin{gathered} {{{\bar {d}}}_{{3\tau }}}\left( {\text{I}} \right) \hfill \\ {{{\bar {d}}}_{{3\tau }}}\left( {{\text{II}}} \right) \hfill \\ \end{gathered} $ |
| 157 | 64 | n | –7148.58(0.90) –7110.62(0.30) |
–7013.4(2.5) –7104(10) |
–7153.4(1.4) –7156.71(9.52) |
–7136.6(6.2) –7231(96) |
28.49(0.71) 30.73(0.19) |
23.2(2.3) 45(18) |
| 165 | 67 | p | –6768.05(0.70) –6839.20(0.79) |
–6921(41) –6855(23) |
–6759.16(0.79) –6810.1(1.9) |
–6825(12) –6808(90) |
–53.37(0.74) –19.4(1.1) |
–12(10) –16(18) |
| 171 | 70 | n | –7337.13(0.09) –7298.42(0.20) |
–7202.1(9.3) –7078(24) |
–7319.47(0.02) –7319.54(0.51) |
–7223(15) –7690(110) |
14.03(0.12) 14.08(0.28) |
–12.6(4.9) –32(24) |
| 175 | 71 | p | –6104.90(0.70) –6276.2(2.6) |
–6380(85) –6133.3(3.1) |
–6083.53(0.86) –6228(10) |
–6139.3(4.5) –6420(190) |
–128.5(2.4) –32.4(6.5) |
–103(22) 9(40) |
| 179 | 72 | n | –6743.4(1.0) –6550.2(1.1) |
–6612(90) –6660(59) |
–6755.0(1.1) –6657.2(2.8) |
–6829(42) –6710(310) |
69.9(1.1) 4.7(1.5) | 9(23) 5(63) |
Таблица 2.
| A | Z | τ | d2τ | d4τ | ||||
|---|---|---|---|---|---|---|---|---|
| А [1] | Б [1] | (а) | (б) | (а) | (б) | |||
| 157 | 64 | n | 196.98(0.32) | 203.5(2.3) | 209.75(0.67) | 218.9(4.6) | –15.33(0.24) | –19.81(0.53) |
| 165 | 67 | p | 628.98(0.55) | 597(20) | 646.93(0.86) | 639(21) | –21.56(0.98) | –18.5(8.1) |
| 171 | 70 | n | 186.63(0.14) | 181.1(7.0) | 174.84(0.30) | 193.4(8.0) | 14.15(0.25) | 5.6(5.7) |
| 175 | 71 | p | 578.9(2.0) | 552(44) | 587.9(5.5) | 545(44) | –10.9(5.5) | 3(18) |
| 179 | 72 | n | 198.58(0.83) | 236(44) | 196.1(1.1) | 219(47) | 3.0(1.4) | –6(18) |
Таблица 3.
Парные энергии Pτ в А [1] и (а) и разности “гладких” масс нечетных ядер $\mathcal{M}$(А [1])–$\mathcal{M}$(Б [1]) и $\mathcal{M}$(а)–$\mathcal{M}$(б) в кэВ. А [1], Б [1], (а), (б) – см. текст
| A | Z | τ | Pτ(А [1]) | $\mathcal{M}$(А [1]) – $\mathcal{M}$(Б [1]) | Pτ(а) | $\mathcal{M}$(а)–$\mathcal{M}$(б) |
|---|---|---|---|---|---|---|
| 157 | 64 | n | 887.2(1.4) | –19(11) | 893.0(1.7) | –35(11) |
| 165 | 67 | p | 862.5(1.3) | –102(25) | 808.6(1.4) | 192(24) |
| 171 | 70 | n | 796.16(0.07) | –82(28) | 790.85(0.14) | –51(23) |
| 175 | 71 | p | 894.2(1.8) | –174(22) | 882.2(2.9) | –376(10) |
| 179 | 72 | n | 743.6(2.0) | 328(63) | 742.5(1.8) | 305(79) |
Как следует из табл. 1, переход от поверхности второго порядка к поверхности четвертого порядка не приводит к уменьшению разброса значений ${{\bar {d}}_{{1\tau }}}$ для различных приближений, а также при разных ΔA внутри приближений (∼3%). Абсолютная величина параметров d3τ почти на два порядка меньше, чем $\left| {{{{\bar {d}}}_{{1\tau }}}} \right|$. В (а) и (б) и внутри этих приближений при разных ΔA в трех случаях из пяти эти параметры довольно сильно отличаются. Для ${}_{{70}}^{{171}}{\text{Yb}}$ в (а) и (б) они отличаются даже знаком. Такие колебания d3τ в разных приближениях ставят под сомнение возможность аппроксимации массовой поверхности как поверхности четвертого порядка. Табл. 1 и табл. 2 показывают, что вывод работы [1] об увеличении эмпирических погрешностей в параметрах массовых поверхностей при увеличении количества ядер, используемых для расчета этих параметров, остается справедливым и при переходе к поверхностям четвертого порядка (ср. A [1] и Б [1], а также (а) и (б)).
В табл. 2 приведены значения четных параметров d2τ, рассчитанных для поверхностей второго и четвертого порядка в различных приближениях, а также значения параметров d4τ, появляющихся в поверхностях четвертого порядка. Как следует из таблицы, расширение массовой поверхности до четвертого порядка не оказывает существенного влияния на близость параметров, определенных по разным группам ядер (ср. A [1] и Б [1], а также (а) и (б)). Изменение группы ядер, по которой происходит расчет параметров, существенно влияет на значения параметров d4τ. Кроме того, сами параметры определяются с большой относительной погрешностью. Эти обстоятельства ставят под вопрос возможность описания масс нечетных атомных ядер полиномами четвертого порядка.
Значения парных энергий Pτ в А [1] и (а) почти совпадают (табл. 3), среднее различие ≈16 кэВ, т.е. относительное различие ∼2%. Как указывалось при обсуждении табл. 1 и 2, расширения массовой поверхности до полинома четвертого порядка по s и t не сближает параметры, определенные по разным группам ядер, в частности, $\mathcal{M}$(а)–$\mathcal{M}$(б) (массовая поверхность четвертого порядка): они остаются примерно такими же, как $\mathcal{M}$(А [1])–$\mathcal{M}$(Б [1]), т.е. вычисленными в предположении, что массовая поверхность может быть аппроксимирована полиномом второго порядка.
Как указывалось во введении (после уравнения (7)) параметры dinkp не являются производными $\left( {{{{{\partial }^{{i + k}}}M(N,Z)} \mathord{\left/ {\vphantom {{{{\partial }^{{i + k}}}M(N,Z)} {{{\partial }^{i}}N{{\partial }^{k}}Z}}} \right. \kern-0em} {{{\partial }^{i}}N{{\partial }^{k}}Z}}} \right)$. Это демонстрируется на следующем частном примере. Исследованные ядра являются стабильными, поэтому при фиксированном A они имеют максимальную энергию связи (B) или минимальную энергию (E = –B), поэтому, если считать параметры производными, то ${{dE} \mathord{\left/ {\vphantom {{dE} {dZ}}} \right. \kern-0em} {dZ}}$ = 0 = ${{dE} \mathord{\left/ {\vphantom {{dE} {dZ - {{dE} \mathord{\left/ {\vphantom {{dE} {dN}}} \right. \kern-0em} {dN}}}}} \right. \kern-0em} {dZ - {{dE} \mathord{\left/ {\vphantom {{dE} {dN}}} \right. \kern-0em} {dN}}}}$ = = ${{\bar {d}}_{{1p}}} - {{\bar {d}}_{{1n}}}$ (${{\bar {d}}_{{1\tau }}} = {{d}_{{1\tau }}} - {{m}_{\tau }}$), A фиксировано (A = Z + + N). Параметры ${{\bar {d}}_{{1\tau }}}$ можно вычислить в Б [1] и (б). Для определенности используем Б [1] и ΔA = = 1. Для нечетно-нейтронных ядер ${{\bar {d}}_{{1p}}} - {{\bar {d}}_{{1n}}}$ = = $ - {{\left[ {o(3, - 2) + o(1, - 2)} \right]} \mathord{\left/ {\vphantom {{\left[ {o(3, - 2) + o(1, - 2)} \right]} 8}} \right. \kern-0em} 8}$, обозначение o(s, t) дано уравнением (12). Для нечетно-протонных s и t должны быть переставлены. Для ${}_{{64}}^{{157}}{\text{Gd,}}$ ${}_{{67}}^{{165}}{\text{Ho,}}$ ${}_{{70}}^{{171}}{\text{Yb,}}$ ${}_{{71}}^{{175}}{\text{Lu}}$ и ${}_{{72}}^{{179}}{\text{Hf,}}$ соответствующие значения ${{\bar {d}}_{{1p}}} - {{\bar {d}}_{{1n}}}$ равны: –8.3 (1.3); –127 (164); 1274 (5); 649 (58); 67 (45), т.е. эти разности параметров явно не равны нулю. Таким образом, этот частный случай подтверждает, что параметры не являются производными. Этот вопрос обсуждался нами ранее для других ядер [10].
ЗАКЛЮЧЕНИЕ
В заключение отметим, что рассмотрено описание массовых поверхностей нечетных стабильных деформированных ядер полиномами четвертого порядка по отклонениям от N и Z нечетного ядра и проведено сравнение с описанием полиномами второго порядка. Показано, что вполне достаточной является аппроксимация второго порядка, т.к. параметры, вычисленные с учетом четвертого порядка, не дают сближения параметров, вычисленных по разным группам ядер, а параметры d3τ (τ = n, p), d4τ (τ = n, p), а также dinkp (i ≠ k; i, k ≠0 ), приведенные ранее для четно-четных ядер в [8], не согласуются между собой.
Список литературы
Власников А.К., Зиппа А.И., Михайлов В.М. // Изв. РАН. Сер. физ. 2020. Т. 84. № 8. С. 1112; Vlasnikov A.K., Zippa A.I., Mikhajlov V.M. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. № 8. P. 919.
Nilsson S.G., Tsang C.F., Sobiczewski A. et al. // Nucl. Phys. A. 1969. V. 131. P. 1.
Соловьев В.Г. Теория сложных ядер. М.: Наука, 1971. 560 с.
Bender M., Heenen P.-H., Reinhard P.-G. // Rev. Mod. Phys. 2003. V. 75. P. 121.
Бор О., Моттельсон Б.Р. Структура атомного ядра. Т. 1. М.: Мир, 1971. 456 с.
Власников А.К., Зиппа А.И., Михайлов В.М. // Изв. РАН. Сер. физ. 2016. Т. 80. С. 989; Vlasnikov A.K., Zippa A.I., Mikhajlov V.M. // Bull. Russ. Acad. Sci. Phys. 2016. V. 80. P. 905.
Madland D.G., Nix J.R. // Nucl. Phys. A. 1988. V. 476. P. 1.
Власников А.К., Зиппа А.И., Михайлов В.М. // Изв. РАН. Сер. физ. 2017. Т. 81. С. 1325; Vlasnikov A.K., Zippa A.I., Mikhajlov V.M. // Bull. Russ. Acad. Sci. Phys. 2017. V. 81. P. 1184.
Wang M., Audi G., Kondev F.G. et al. // Chin. Phys. C. 2017. V. 41. № 3. Art. № 030003.
Mikhajlov V.M., Vlasnikov A.K., Zippa A.I. // Int. Sci. Forum “Nuclear Science and Technologies” (Almaty, 2017). P. 56.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая