1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 12, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 12, стр. 1743-1745

Бездифракционные импульсы Матье в среде углеродных нанотрубок, в условиях оптического резонатора

Ю. В. Двужилова 1, А. М. Белоненко 1, И. С. Двужилов 1, *, М. Б. Белоненко 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Волгоградский государственный университет”
Волгоград, Россия

* E-mail: dvuzhilov.ilya@volsu.ru

Поступила в редакцию 15.07.2020
После доработки 10.08.2020
Принята к публикации 26.08.2020

Полный текст (PDF)

Аннотация

Теоретически исследовано распространение трехмерных предельно коротких оптических импульсов в среде полупроводниковых углеродных нанотрубок, в условиях цилиндрического оптического резонатора. Импульсы имеют поперечное сечение, задаваемое функциями Матье. С помощью численного моделирования показано, что такие импульсы распространяются устойчиво, сохраняя при этом свою энергию в ограниченной пространственной области. Импульс испытывает отражение от стенок оптического резонатора и дальнейшую интерференцию. Расчеты проводились на временах до 140 пс, что имеет важное значение для возможных практических приложений.

ВВЕДЕНИЕ

В настоящее время для нелинейной оптики существенный интерес представляют бездифракционные оптические пучки (Бесселева, Эйри и Матье сечения), которые представляют собой, импульсы, распространяющиеся без изменения формы и амплитуды. Дифракционное расплывание импульсов является фундаментальной особенностью свободно распространяющихся оптических лучей, которые легко наблюдаются в повседневной жизни. Как известно, дифракция оказывает значительное влияние на предел оптического разрешения в различных отраслях, в том числе, в микроскопии, литографии и фотографии, а также на предел точности спектрального анализа [1]. Таким образом, бездифракционные пучки имеют ряд преимуществ перед другими лучами сопоставимого поперечного размера, а именно, сдерживание уширения формы и масштаба импульса во время его распространения.

Важно, чтобы среда, в которой распространяются импульсы, обладала нелинейными свойствами, в качестве такой среды, подходят полупроводниковые углеродные нанотрубки, часто используемые в различных приложениях [2–4]. Здесь нелинейность возникает из-за того, что закон дисперсии электронов, которые находятся в зоне проводимости, не параболичен, таким образом, зависимость тока от приложенного электрического поля является нелинейной. Благодаря моделированию такой нелинейной среды становится возможным управление некоторыми параметрами предельно короткого оптического импульса Матье, например, его скоростью и формой, что в свою очередь играет большую роль в создании современной элементной базы опто- и наноэлектроники.

Отметим, что среда углеродных нанотрубок помещена в условия оптического резонатора. Рассматриваемый цилиндрический резонатор, является идеальным проводником, т.е. отсутствуют свободные заряды, электрическое поле на границе равно нулю. Эти начальные условия выбраны с целью минимизации потерь энергии импульса. В случае если наблюдается локализация энергии импульса, то такого рода пространственно локализованные структуры принято называть резонаторными солитонами [5].

Следует заметить, что импульсы Матье были получены экспериментально [6], таким образом, исследование их динамики в среде углеродных нанотрубок, помещенных в оптический резонатор, является весьма актуальным не только с теоретической точки зрения, но возможно будет иметь значение и для практических приложений.

ОСНОВНЫЕ УРАВНЕНИЯ

В данной работе не будут рассмотрены: наведенный импульсом заряд вдоль оси углеродных нанотрубок, а также электрическое поле подложки. Характерное расстояние между нанотрубками и их размер во много раз меньше, чем размер пространственной области, в которой локализован трехмерный предельно короткий импульс Матье. Это позволяет считать ток распространенным по объему, и применить приближение сплошной среды.

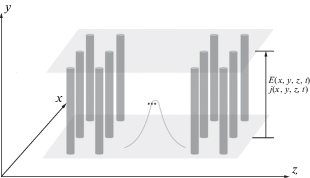
Предполагаемая система смоделирована таким образом, что: импульс распространяется в среде углеродных нанотрубок типа zig-zag, электрическое поле которого направлено вдоль оси нанотрубок (рис. 1).

Рис. 1.

Геометрия задачи. Ток и электрическое поле импульса направлены вдоль оси углеродных нанотрубок. Единица по τ и σ соответствует 2 · 10–7 м.

Одноэлектронный спектр, в отсутствии кулоновского отталкивания, для углеродных нанотрубок типа “zig-zag” (m, 0) имеет вид [7, 8]:

(1)
$\begin{gathered} {{\varepsilon }_{s}}({\mathbf{p}}) = \\ = \,\, \pm \gamma {{\left\{ {1 + 4\cos (a{\mathbf{p}})\cos \left( {\pi \frac{s}{m}} \right) + 4{{{\cos }}^{2}}\left( {\pi \frac{s}{m}} \right)} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $
где $s = 1,2...m,$ $\gamma \approx 2.7$ эВ, $a = {{3b} \mathord{\left/ {\vphantom {{3b} {2\hbar }}} \right. \kern-0em} {2\hbar }},$ $b = 0.142$ нм расстояние между соседними атомами углерода.

Уравнения Максвелла в параболической системе координат можно записать в виде:

(2)
$\begin{gathered} \frac{1}{{{{u}^{2}} + {{w}^{2}}}}\left( {\frac{1}{u}\frac{\partial }{{\partial u}}\left( {u\frac{{\partial{ \bar {A}}}}{{\partial u}}} \right) + \frac{1}{w}\frac{\partial }{{\partial w}}\left( {w\frac{{\partial{ \bar {A}}}}{{\partial w}}} \right)} \right) - \\ - \,\,\frac{\varepsilon }{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\bar {A}}}{{\partial {{t}^{2}}}} + \frac{1}{{{{u}^{2}}{{w}^{2}}}}\frac{{{{\partial }^{2}}\bar {A}}}{{\partial {{\varphi }^{2}}}} + \frac{{4\pi }}{c}\bar {j} = 0. \\ \end{gathered} $

Здесь ε – диэлектрическая проницаемость среды, c – скорость света, u, w, φ – параболические координаты, $\bar {A}$ – вектор-потенциал электрического поля импульса, $\bar {j}$ – плотность электрического тока. Граничные условия на границе резонатора, соответствуют граничным условиям для случая идеально проводящего проводника.

Здесь плотность тока можно представить в виде:

(3)
$\begin{gathered} j = - e\sum\limits_k {{{B}_{k}}\sin \left( {\frac{{ke}}{c}A(t)} \right)} , \\ {{B}_{k}} = \sum\limits_{s = 1}^m {\int\limits_{{{ - {\pi }} \mathord{\left/ {\vphantom {{ - {\pi }} a}} \right. \kern-0em} a}}^{{{\pi } \mathord{\left/ {\vphantom {{\pi } a}} \right. \kern-0em} a}} {dp} } {{A}_{{ks}}}\cos (kp)\frac{{\exp ( - \beta {{\varepsilon }_{s}}(p))}}{{1 + \exp ( - \beta {{\varepsilon }_{s}}(p))}} \\ \end{gathered} $

${{A}_{{ks}}} = \int_{{{ - {\pi }} \mathord{\left/ {\vphantom {{ - {\pi }} a}} \right. \kern-0em} a}}^{{{\pi } \mathord{\left/ {\vphantom {{\pi } a}} \right. \kern-0em} a}} {{{\upsilon }_{s}}(p)\sin (kp)dp} $ – убывающие с ростом k коэффициенты разложения, ${{\upsilon }_{s}}(p) = {{\partial {{\varepsilon }_{s}}(p)} \mathord{\left/ {\vphantom {{\partial {{\varepsilon }_{s}}(p)} {\partial p}}} \right. \kern-0em} {\partial p}}$ – групповая скорость, $\beta = {1 \mathord{\left/ {\vphantom {1 {kT}}} \right. \kern-0em} {kT}}.$

Интегрирование ведется в первой зоне Бриллюена. Количество членов разложения в суммы (3) зависит от желаемой точности решения, в нашем случае точность составляет восемь значащих знаков. Отметим, что закон дисперсии электронов (1) учтен в (3) точно.

Далее мы полагаем, что в уравнении (2) производной по углу можно пренебречь, благодаря параболической симметрии. Например, в работе [9] было показано, что из-за неоднородности электрического поля, может происходить накопление заряда в определенной области, однако для предельно коротких импульсов ей можно пренебречь, из-за малой длительности импульса (фемтосекунды).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Уравнение (2), с учетом (3), решалось численно, при помощи явной конечно-разностной схемы [10]. Шаг по времени и координате определялся из условий устойчивости численной схемы.

Начальное условие для вектор-потенциала электрического поля трехмерного предельно короткого оптического импульса Матье выбиралось в виде:

(4)
$\begin{gathered} A\left( {u,w,0} \right) = Yc{{e}_{0}}(1,q)Jce\left( {\frac{w}{{{{\gamma }_{w}}}}} \right)\exp \left( { - \frac{{{{{\left( {u - {{u}_{0}}} \right)}}^{2}}}}{{{{\gamma }_{u}}}}} \right) \times \\ \times \,\,\exp \left( { - \frac{w}{{{{\gamma }_{w}}}}} \right),\,\,\,\,\frac{{dA\left( {u,w,0} \right)}}{{dt{\kern 1pt} '}} = \\ = Y\frac{{2V\left( {u - {{u}_{0}}} \right)c{{e}_{0}}(1,q)}}{{{{\gamma }_{u}}^{2}}}Jce\left( {\frac{w}{{{{\gamma }_{w}}}}} \right) \times \\ \times \,\,\exp \left( { - \frac{{{{{\left( {u - {{u}_{0}}} \right)}}^{2}}}}{{{{\gamma }_{u}}}}} \right)\exp \left( { - \frac{w}{{{{\gamma }_{w}}}}} \right), \\ \end{gathered} $
где Y – амплитуда импульса, V – начальная скорость импульса, γu и γw – ширина импульса вдоль u и w осей, u0 – начальная координата центра импульса по оси u, Jce(w), $c{{e}_{0}}(1,q)$ – функции Матье [11].

Результаты эволюции трехмерного предельно короткого импульса, имеющего Матье профиль, распространяющего в среде углеродных нанотрубок, помещенных в оптический резонатор, представлены на рис. 2. Продемонстрировано устойчивое распространение трехмерного предельно короткого бездифракционного импульса Матье, который распространяется в среде углеродных нанотрубок, помещенных в условия оптического резонатора. Импульс сохраняет свою энергию локализованной в ограниченной пространственной области, которая сосредоточена вдоль оси цилиндрического резонатора, на временах до 100 пс.

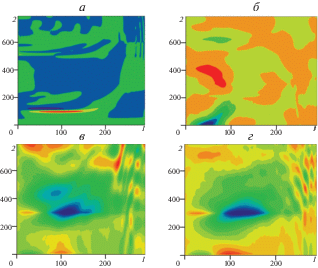
Рис. 2.

Эволюция бездифракционного трехмерного предельно короткого оптического импульса Матье в среде углеродных нанотрубок, в условиях оптического резонатора, в фиксированные моменты времени: 10 (а), 40 (б), 70 (в), 100 пс (г). По осям отложены единицы координат в микрометрах (1 – u, 2 – w). Цветом показана напряженность электрического поля импульса (увеличивается от синего к красному).

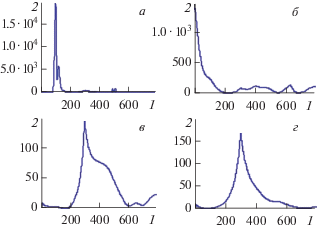
На рис. 3 показаны срезы импульса, проходящие через определенную точку оси u, в различные моменты времени. Из рисунка видно, что вся энергия импульса сосредоточена в сечении резонатора. Формирование такой устойчивой структуры происходит благодаря отражению волн от стенок резонатора и их дальнейшей интерференции.

Рис. 3.

Срезы интенсивности бездифракционного трехмерного предельно короткого импульса Матье, вдоль оси u, в различные моменты времени 10 (а), 40 (б), 70 (в), 100 пс (г). По осям отложены единицы координат (мкм) и электрического поля (В/мкм).

ЗАКЛЮЧЕНИЕ

Из проведенного исследования можно сделать следующий вывод: бездифракционные трехмерные предельно короткие импульсы Матье, распространяются устойчиво в среде углеродных нанотрубок, в условиях оптического резонатора. Энергия импульса остается локализованной в ограниченной пространственной области. Эволюционируя во времени, импульс двигается от оси резонатора к его стенкам, отражаясь от них, и затем происходит интерференция встречных волн, за счет которой импульс сохраняет свою энергию сосредоточенной, с небольшим изменением формы.

Таким образом, появляется возможность контролировать уширение импульса вдоль оси резонатора. Следует отметить, что численное моделирование динамики импульсов проводилось на больших временах, что обуславливает важность полученных результатов для практических приложений.

Двужилова Ю.В., Двужилов И.С., Белоненко М.Б. выражают благодарность Министерству науки и высшего образования РФ в рамках государственного задания за поддержку численного моделирования (проект № 0633-2020-0003).

Список литературы

  1. Bandres M.A., Gutiérrez-Vega J.C., Chávez-Cerda S. // Opt. Lett. 2004. V. 29. P. 44.

  2. Jiang J.-W., Wang J.-S. // J. Appl. Phys. 2011. V. 110. Art. № 124319.

  3. Leblond H., Mihalache D. // Phys. Rev. A. 2012. V. 86. Art. № 043832.

  4. Belonenko M., Demushkina E.V., Lebedev N.G. // J. Rus. Laser Res. 2006. V. 27. P. 457.

  5. Кившарь Ю.С., Агравал Г.П. Оптические солитоны. От световодов к фотонным кристаллам. М.: Физматлит, 2005. 649 с.

  6. Gutiérrez-Vega J.C., Iturbe-Castillo M.D., Ramı́rez G.A. // Opt. Commun. 2001. V. 195. P. 35.

  7. Елецкий А.В. // УФН. 1997. Т. 167. № 9. С. 945; Eletskii A.V. // Phys. Usp. 1997. V. 40. № 9. P. 899.

  8. Dresselhaus M.S., Dresselhaus G., Eklund P.C. Science of fullerenes and carbon nanotubes. San Diego: Academic Press, 1996. 965 p.

  9. Zhukov A.V., Bouffanais R., Fedorov E.G. et al. // J. Appl. Phys. 2013. V. 114. Art. № 143106.

  10. Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). М.: Наука, 1975. 632 с.

  11. Абрамовиц М., Стиган И. Справочник по специальным функциям, с формулами, графиками и математическими таблицами. М.: Наука, 1979. 832 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал