1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 12, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 12, стр. 1707-1711

Автомодельные оптические импульсы в средах с квадратичной нелинейностью и поглощением

А. А. Калинович 1, *, И. Г. Захарова 1, М. В. Комиссарова 1, Т. М. Лысак 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

* E-mail: kalinovich@gmail.com

Поступила в редакцию 15.07.2020
После доработки 10.08.2020
Принята к публикации 26.08.2020

Полный текст (PDF)

Аннотация

Изучены возможности формирования и сохранения двухчастотного солитоноподобного состояния с учетом влияния двухфотонного поглощения. В ходе численного эксперимента, выявлено негативное влияние дисперсии третьего порядка на сохранение автомодельного режима.

ВВЕДЕНИЕ

Изучение солитоноподобных импульсов, распространяющихся в естественных и искусственных нелинейных средах с диссипацией, является одной из наиболее интересных задач современной нелинейной фотоники [1–3]. В отличие от традиционных солитонов, которые могут распространяться на большие расстояния без изменения своей формы в консервативных системах, солитоноподобные импульсы или квазисолитоны характерны именно для диссипативных систем. Теряя энергию, такие импульсы, тем не менее, сохраняют свою форму и не испытывают аберраций.

В экспериментальных работах последних лет выявлено, что при высоких интенсивностях лазерного излучения (порядка 1 ГВт/см2) существенное влияние на солитоноподобные режимы распространения импульсов оказывает не только линейное, но и нелинейное двухфотонное поглощение. Так, в работе [4] подчеркивается, что эффекты двухфотонного поглощения (ДФП) влияют на распространение солитонов в кремнии. Авторы статьи сообщают о первой экспериментальной демонстрации сжатия импульса солитонным эффектом в кремнии, несмотря на ДФП и генерацию свободных носителей при распространении пикосекундного импульса. Влияние многофотонного поглощения (МФП) на распространение лазерного импульса в фотонно-кристаллических волноводах с медленным светом обсуждается в [5].

Подавление двухфотонного поглощения в материале GaInP имеет решающее значение для экспериментального наблюдения оптических солитонов и сжатия импульсов в фотонно-кристаллических волноводах длиной один миллиметр [6].

Достаточно традиционным методом формирования солитонов в средах c поглощением является искусственное введение усиления [1, 7]. Так, например, возможность формирования диссипативных пространственных солитонов была показана для лазеров с насыщаемым усилением и поглощением [8], в системах, в которых эволюция света регулируется комплексным уравнением Гинзбурга–Ландау [9], а также в полупроводниковых усилителях [10].

Солитоноподобные режимы можно наблюдать в диссипативных средах и без дополнительного усиления. Например, автомодельные решения нелинейного уравнения Шрёдингера, существенно отличающиеся от классических солитонов, были найдены в работах [11, 12]. Частота таких солитоноподобных импульсов изменялась во времени. Влияние как линейного, так и нелинейного поглощения на подобные структуры было исследовано в дальнейших работах. Например, в статье [13] аналитически найдена форма оптического автомодельного импульса, распространяющегося в среде конечной длины с однофотонным нестационарным поглощением. Двух- и трехфотонное поглощение нелинейного характера в случае взаимодействия лазерного излучения с исследуемым веществом рассматривалось в работах [14, 15]. Отметим, что исследования в работах [11–15] были сконцентрированы на одиночных солитонах в средах с кубической нелинейностью.

По сравнению с последними солитоны и солитоноподобные импульсы на квадратичной нелинейности имеют более низкий порог генерации, хотя их поиск и представляет достаточно сложную с математической точки зрения задачу из-за параметрической связи. Еще сильнее задача усложняется при исследовании импульсов короче 4–5 пс, когда необходимо учитывать нелинейные и дисперсионные эффекты высших порядков [1]. Квадратичным параметрически связанным солитонам с изменяющейся частотой при ненулевой дисперсии третьего порядка посвящена наша недавняя работа [16], в которой была показана возможность формирования автомодельных импульсов в квадратично-нелинейной среде при учете как линейного, так и нелинейного поглощения. Однако, влияние эффектов высших порядков, играющих роль при формировании двухчастотных солитоноподобных состояний, было изучено недостаточно подробно.

Настоящая работа является логичным продолжением исследований, начатых в [16]. Наши вычисления основываются на системе параболических уравнений, описывающей удвоение высокоинтенсивного ультракороткого оптического импульса в среде с линейным (однофотонным) и нелинейным (двухфотонным) поглощением. Учитывая влияние линейного и нелинейного поглощения, мы изучаем роль дисперсии третьего порядка при формировании и сохранении автомодельного режима распространения импульсов.

ПОСТАНОВКА ЗАДАЧИ

Cистема безразмерных параболических уравнений, описывающих удвоение высокоинтенсивного ультракороткого оптического импульса в среде с линейным (однофотонным) и нелинейным (двухфотонным) поглощением, имеет следующий вид [16]:

(1)
$\begin{gathered} i\frac{{\partial {{A}_{1}}}}{{\partial z}} + i\delta \frac{{\partial {{A}_{1}}}}{{\partial t}} = - {{D}_{{21}}}\frac{{{{\partial }^{2}}{{A}_{1}}}}{{\partial {{t}^{2}}}} + i{{D}_{{31}}}\frac{{{{\partial }^{3}}{{A}_{1}}}}{{\partial {{t}^{3}}}} - \\ - \,\,i{{\gamma }_{1}}{{A}_{1}} - i{{\alpha }_{1}}{{\left| {{{A}_{1}}} \right|}^{2}}{{A}_{1}} + A_{1}^{*}{{A}_{2}}{{e}^{{i{\Delta }kz}}}, \\ i\frac{{\partial {{A}_{2}}}}{{\partial z}} - i\delta \frac{{\partial {{A}_{2}}}}{{\partial t}} = - {{D}_{{22}}}\frac{{{{\partial }^{2}}{{A}_{2}}}}{{\partial {{t}^{2}}}} + i{{D}_{{32}}}\frac{{{{\partial }^{3}}{{A}_{2}}}}{{\partial {{t}^{3}}}} - \\ - \,\,i{{\gamma }_{2}}{{A}_{2}} - i{{\alpha }_{2}}{{\left| {{{A}_{2}}} \right|}^{2}}{{A}_{2}} + \frac{{A_{1}^{2}}}{2}{{e}^{{ - i{\Delta }kz}}}. \\ \end{gathered} $

Здесь ${{A}_{1}}(z,t)$ и ${{A}_{2}}(z,t)$ – медленно меняющиеся амплитуды на основной и удвоенной частоте, z – направление распространения импульса, t – время, δ – расстройка групповых скоростей, ${{D}_{{21}}},$ ${{D}_{{22}}},$ ${{D}_{{31}}},$ ${{D}_{{32}}}$ – коэффициенты дисперсии второго и третьего порядков соответственно, ${{\gamma }_{1}},$ ${{\gamma }_{2}}$ и ${{\alpha }_{1}},$ ${{\alpha }_{2}}$ – коэффициенты линейного и нелинейного поглощения соответственно, $\Delta k$ – расстройка фазовых скоростей. Все описанные величины безразмерны. Уравнения (1) решаются с граничными условиями:

(2)
$\begin{gathered} {{A}_{{1,2}}}(z,t = 0) = \frac{{\partial {{A}_{{1,2}}}}}{{\partial t}}(z,t = 0) = {{A}_{{1,2}}}(z,{{L}_{t}}) = 0, \\ {\text{0}} \leqslant z \leqslant {{L}_{z}} \\ \end{gathered} $

и с начальным распределением комплексной амплитуды:

(3)
$\begin{gathered} {{A}_{1}}(z = 0,t) = {{A}_{{in}}}(t),\,\,\,\,{{A}_{2}}(z = 0,t) = 0, \\ 0 \leqslant t \leqslant {{L}_{t}}, \\ \end{gathered} $
где ${{L}_{z}}$ – нормированная длина нелинейной среды, и ${{L}_{t}}$ – интервал времени, в течение которого происходит анализ взаимодействия импульса со средой.

Рассмотрим предел, отвечающий большим положительным значениям расстройки фазовых скоростей. Он известен как каскадный предел, так как в этом случае два квадратичных эффекта связываются каскадным образом и приводят к эффективной кубической нелинейности керровского типа.

Для того, чтобы рассмотреть поведение импульса при каскадном пределе, необходимо провести некоторые преобразования [17]. Сделаем замену $\overline {{{A}_{2}}} = {{A}_{2}}{{e}^{{i{\Delta }kz}}}.$ Полагаем $\Delta k \gg 1,$ что позволяет пренебречь производными $\frac{{\partial {{{\bar {A}}}_{2}}}}{{\partial z}},$ $\frac{{\partial {{{\bar {A}}}_{2}}}}{{\partial t}},$ $\frac{{{{\partial }^{2}}{{{\bar {A}}}_{2}}}}{{\partial {{t}^{2}}}},$ $\frac{{{{\partial }^{3}}{{{\bar {A}}}_{2}}}}{{\partial {{t}^{3}}}}.$ Пренебрегаем ДФП для второй гармоники и получаем:

(4)
${{\bar {A}}_{2}} = {{A_{1}^{2}} \mathord{\left/ {\vphantom {{A_{1}^{2}} {\left( {\Delta k + i{{\gamma }_{2}}} \right)}}} \right. \kern-0em} {\left( {\Delta k + i{{\gamma }_{2}}} \right)}}.$

В результате несложных математических преобразований приходим к стандартному нелинейному уравнению Шрёдингера (НУШ):

(5)
$\begin{gathered} \frac{{\partial {{A}_{1}}}}{{\partial z}} + i{{D}_{{21}}}\frac{{{{\partial }^{2}}{{A}_{1}}}}{{\partial {{t}^{2}}}} + {{D}_{{31}}}\frac{{{{\partial }^{3}}{{A}_{1}}}}{{\partial {{t}^{3}}}} + {{\gamma }_{1}}{{A}_{1}} + \left( {i\mu + {{\alpha }_{1}}} \right) \times \\ \times \,\,{{\left| {{{A}_{1}}} \right|}^{2}}{{A}_{1}} = 0,\,\,\,\,0 \leqslant z \leqslant {{L}_{z}},\,\,\,\,0 \leqslant t \leqslant {{L}_{t}}. \\ \end{gathered} $

Как известно [1], НУШ (5) имеет решения в виде светлых или темных солитонов. Это доказывает возможность существования солитонов типа НУШ в средах с квадратичной нелинейностью.

Представим чирпированное солитоноподобное решение задачи (1)–(3) в виде ${{A}_{1}}{\text{(}}z{\text{,}}t) = \rho (z,t){{e}^{{i{\varphi }(z,t)}}},$ где $\rho $ и $\varphi $ – действительные функции, описывающие амплитуду и фазу. Далее предполагаем [18]:

(6)
$\begin{gathered} \rho \left( {z,\bar {t}} \right) = \sqrt {I\left( {z,\bar {t}} \right)} ,\,\,\,\,I\left( {z,\bar {t}} \right) = {{I}_{0}}(z) \times \\ \times \,\,\left( {1 + \sum\limits_{j = 1}^4 {{{b}_{j}}t{{h}^{j}}\left( {{{\bar {t}} \mathord{\left/ {\vphantom {{\bar {t}} {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}}} \right)} } \right),\,\,\,\,\frac{{\partial \varphi (z,t)}}{{\partial t}} = a + dth\left( {{{\bar {t}} \mathord{\left/ {\vphantom {{\bar {t}} {{{\tau }_{p}}}}} \right. \kern-0em} {{{\tau }_{p}}}}} \right), \\ \bar {t} = {{t - {{L}_{t}}} \mathord{\left/ {\vphantom {{t - {{L}_{t}}} 2}} \right. \kern-0em} 2}, \\ \end{gathered} $
где параметры ${{\tau }_{p}}{\text{,}}$ $a,$ ${{b}_{j}},$ $d$ – константы. Параметр ${{\tau }_{p}}$ характеризует длительность импульса, а остальные параметры описывают форму импульса и чирпа. ${{I}_{0}}\left( z \right)$ – функция, определяющая убывание амплитуды импульса в процессе распространения.

Остановимся подробнее на связи решения (6) с традиционными автомодельными решениями. Тридцать лет назад в работах [19, 20] впервые сообщалось о том, что решения типа бегущей волны отдельных нелинейных волновых уравнений могут быть найдены в виде функций гиперболического тангенса. С тех пор этот метод достаточно часто используется в нелинейной математической физике [21]. Также известно, что независимые переменные, входящие в решение типа бегущей волны, можно записать через натуральные логарифмы соответствующих независимых переменных, входящих в автомодельное решение [22].

В [16] показано, что при специальном подборе параметров формулы (6) описывают самоподобное распространение лазерного излучения в каскадном пределе. Для этого используются квазисолитоны (6) в качестве начального распределения комплексной амплитуды на основной частоте для (1). При численном моделировании контролируется следующая мера отклонения:

$\Delta = \mathop {max}\limits_t \left( {{{\left( {{{{\left| {{{A}_{{teor}}}} \right|}}^{2}} - {{{\left| {{{A}_{{calc}}}} \right|}}^{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\left| {{{A}_{{teor}}}} \right|}}^{2}} - {{{\left| {{{A}_{{calc}}}} \right|}}^{2}}} \right)} {{{{\left| {{{A}_{{max}}}} \right|}}^{2}}}}} \right. \kern-0em} {{{{\left| {{{A}_{{max}}}} \right|}}^{2}}}}} \right),$
где ${{\left| {{{A}_{{calc}}}} \right|}^{2}}$ – интенсивность импульса основной частоты, рассчитанная численно, ${{\left| {{{A}_{{teor}}}} \right|}^{2}}$ – интенсивность, рассчитанная с использованием формулы (6) с длительностью и максимальной амплитудой, равными значениям, взятым из численного моделирования.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

При больших $\Delta k$ описание распространения двух волн сводится, фактически, к описанию распространения одной волны [16]. Так как нами исследуется режим генерации второй гармоники, отметим, что импульсы выходят на автомодельный режим распространения не сразу, а только после того, как импульс накачки пройдет расстояние, достаточное для генерации второй гармоники.

Уравнения (1) решались численно. Были рассмотрены случаи преобладания дисперсии второго или третьего порядков, а также их одновременное влияние. На рис. 1 показаны профили интенсивности, рассчитанные при влиянии только дисперсии второго порядка. В процессе генерации второй гармоники происходит образование связанного состояния, которое, однако, не является солитоном. Уже при z = 10 на второй гармонике присутствует целая серия пиков, интенсивность которых невысока. При этом амплитудный профиль основной частоты вначале, при интенсивной генерации второй гармоники достаточно сильно отклоняется от автомодельного. Но затем это отклонение несколько уменьшается, что свидетельствует о том, что чирп пучка сохраняется.

Рис. 1.

Профили амплитуды, рассчитанные численно (сплошная линия для обеих гармоник) и согласно формуле (6) (штриховая линия для основной частоты и штрих-пунктирная для второй гармоники), распределение фазы (пунктирная линия для основной частоты и штрих-пунктир-пунктирная для второй гармоники) при z = 0 (а), z = 5 (б), z = 10 (в). Отклонение теоретического и рассчитанного амплитудного профиля Δ (г). Параметры начального профиля ${{\tau }_{p}} = 1,$ $a = 1,$ ${{b}_{1}} = - {{b}_{3}} = - 1,$ ${{b}_{2}} = - 0.75,$ ${{b}_{4}} = - 0.25,$ $d = - 1.$ Коэффициенты поглощения ${{\gamma }_{1}}$ = ${{\gamma }_{2}}$ = 0.01 и ${{\alpha }_{1}}$ = ${{\alpha }_{2}}$ = = 0.1. Фазовая расстройка Δk = 3. Сильная дисперсия второго порядка ${{D}_{{21}}} = 0.1,$ ${{D}_{{22}}} = 0.2,$ нулевая дисперсия третьего порядка ${{D}_{{31}}} = 0,$ ${{D}_{{32}}} = 0.$

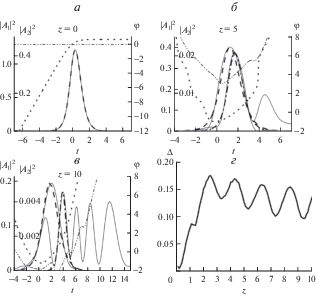
На рис. 2 приведены профили интенсивностей при одновременном влиянии дисперсий второго и третьего порядков. В данном случае состояние можно условно считать связанным, вторая гармоника быстрее разделяется на отдельные пики. Но при этом профиль основной частоты сохраняет чирп, что следует из того, что после прохождения трассы z = 3 отклонение от аналитического профиля (6) не возрастает.

Рис. 2.

Аналогично рис. 1. Сильная дисперсия второго порядка ${{D}_{{21}}} = 0.1,$ ${{D}_{{22}}} = 0.2$ при наличии дисперсии третьего порядка ${{D}_{{31}}} = 0.02,$ ${{D}_{{32}}} = 0.04.$

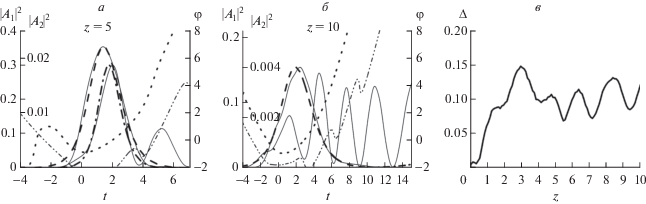
На рис. 3 изображены профили интенсивностей при преобладании дисперсии третьего порядка. Связанное состояние здесь сохраняется и при z = 10, хотя вторая гармоника демонстрирует наличие значительного хвоста. Отклонения рассчитанного профиля основной частоты от формы (6) вначале нарастают, но на расстоянии больше z = 2 постепенно уменьшаются. Это говорит о том, что в данном случае форма импульса ближе к чирпированной.

Рис. 3.

Аналогично рис. 1. Слабая дисперсия второго порядка ${{D}_{{21}}} = 0.001,$ ${{D}_{{22}}} = 0.002$ при наличии дисперсии третьего порядка ${{D}_{{31}}} = 0.02,$ ${{D}_{{32}}} = 0.04.$

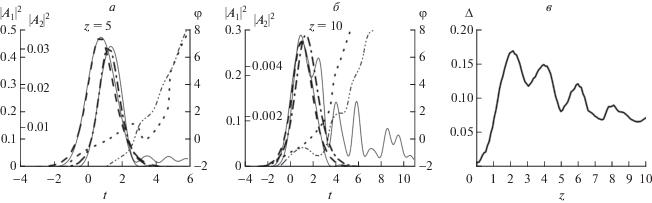
ЗАКЛЮЧЕНИЕ

В настоящей статье рассмотрена генерация второй гармоники в квадратично-нелинейной среде с двухфотонным поглощением. Основной интерес исследования представляла проверка возможности формирования и сохранения автомодельного режима распространения связанного состояния импульса основной и второй гармоники.

При высоких интенсивностях падающего лазерного излучения и ультракоротких длительностях импульсов необходимо учитывать нелинейные и дисперсионные эффекты высших порядков. В связи с этим в работе численно решалась система параболических нелинейных уравнений, в которых помимо дисперсии второго порядка была учтена еще и дисперсия третьего порядка, а помимо линейного поглощения – еще и двухфотонное поглощение.

Нами показано, что при больших волновых расстройках (в каскадном пределе), система параметрически связанных уравнений переходит в нелинейное уравнение Шредингера, имеющего в зависимости от входящих в него коэффициентов различные солитоноподобные решения. Исходя из этого, решение системы уравнения было целесообразно искать в виде чирпированных импульсов.

Совместное влияние нелинейности, дисперсии различных порядков, линейного и нелинейного поглощения приводит к многопараметрической задаче. Нами последовательно изучено влияние этих факторов на автомодельный вид распространяющихся импульсов. В отличие от одиночных солитонов на кубической нелинейности, парные солитоны на квадратичной нелинейности должны двигаться как единое целое, что являлось одним из критериев автомодельности.

При учете двухфотонного поглощения отмечается нарушение совпадения центров импульсов основной и второй гармоник, а также возникновение осциллирующих хвостов с обеих сторон импульса.

Учет дисперсии третьего порядка оказывает негативное влияние на сохранение автомодельного вида двухцветного солитоноподобного импульса: появляется модуляция хвостов, ассиметрия, смещение положения центра “тяжести” влево или вправо.

Исследование выполнено при финансовой поддержке Российского научного фонда (проект № 17-11-01157).

Список литературы

  1. Kivshar Yu.S., Agrawal G.P. Optical solitons: from fibers to photonic crystals. Amsterdam: Academic Press, 2003. 540 p.

  2. Егоров О.А., Захарова И.Г., Сухоруков А.П. // Изв. РАН. Сер. физ. 2002. Т. 66. № 12. С. 1798; Egorov O.A., Zakharova I.G., Sukhorukov A.P. // Bull. Russ. Acad. Sci. Phys. 2002. V. 66. № 12. P. 1803.

  3. Sazonov S., Kalinovich A., Zakharova I., Komissarova M. et al. // EPJ Web Conf. 2017. V. 161. Art. № 02009.

  4. Blanco-Redondo A., Husko C., Eades D. et al. // Nat. Commun. 2014. V. 5. P. 3160.

  5. Husko C.A., Colman P., Combri S. et al. // Opt. Lett. 2011. V. 36. № 12. P. 2239.

  6. Colman P., Husko C., Combrie S. et al. // Nat. Photon. 2010. V. 4. P. 862.

  7. Lobanov V.E., Borovkova O.V., Malomed B.A. // Phys. Rev. A. 2014. V. 90. Art. № 053820.

  8. Rosanov N.N. Spatial hysteresis and optical patterns. N.Y.: Springer, 2010. 308 p.

  9. Akhmediev N., Ankiewicz A. Dissipative solitons: from optics to biology and medicine. N.Y.: Springer, 2008. 479 p.

  10. Ultanir E.A., Stegeman G.I., Michaelis D. et al. // Phys. Rev. Lett. 2003. V. 90. Art. № 253903.

  11. Xu Q.Q., Yao D.Z., Liu X.N. et al. // Phys. Rev. A. 2012. V. 86. № 2. Art. № 023853.

  12. Захарова И.Г., Калинович А.А., Трофимов В.А. // Опт. и спектроск. 2018. Т. 124. № 4. С. 499; Zakharova I.G., Kalinovich A.A., Trofimov V.A. // Opt. Spectrosс. 2018. V. 124. № 4. P. 516.

  13. Colman P., Husko C., Combrie S. et al. // Nat. Photon. 2010. V. 4. P. 862.

  14. Barenblatt G.I. Scaling, self-similarity, and intermediate asymptotics. Cambridge: Cambridge Univ. Press, 1996. 386 p.

  15. Trofimov V.A., Lysak T.M., Zakharova I.G. // J. Phys. Conf. Ser. 2016. V. 691. № 1. Art. № 012013.

  16. Kalinovich A.A., Komissarova M.V., Lysak T.M. et al. // Proc. SPIE. 2020. V. 11358. Art. № 113581Z.

  17. Agrawal G.P. Nonlinear fiber optics. Boston: Academic Press, 2007. 648 p.

  18. Malfliet W. // Amer. J. Phys. 1992. V. 60. P. 650.

  19. Huibin L., Kelin W. // J. Phys. A. 1990. V. 23. P. 4097.

  20. Hereman W., Banerjee P.R., Korpel A. et al. // J. Phys A. 1986. V. 19. P. 607.

  21. Кудряшов Н.А. Методы нелинейной математической физики. М.: МИФИ, 2008. 352 с.

  22. Полянин А.Д. Нелинейные уравнения математической физики и механики. Методы решения. М.: Юрайт, 2018. 256 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал