1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 12, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 12, стр. 1719-1724

Магический изомер нанокластера золота Au20: топологическая модель и спектральные характеристики

Т. А. Худайберганов 1, П. П. Худобин 1, С. М. Аракелян 1, *

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых
Владимир, Россия

* E-mail: arak@vlsu.ru

Поступила в редакцию 15.07.2020
После доработки 10.08.2020
Принята к публикации 26.08.2020

Полный текст (PDF)

Аннотация

Методом функционала плотности на основе моделей самосогласованного поля с учетом плотностей энергетических электронных состояний исследуются спектральные характеристики магического нанокластера Au20 С использованием различных программных инструментов численного моделирования получены спектры и плотность электронных состояний нанокластеров этого типа и сделаны выводы об оптических свойствах тетраэдрального нанокластера Au20. Кратко обсуждается перспективы их использования в практических приложениях.

ВВЕДЕНИЕ

Нанокластер Au20, состоящий из 20 атомов, характеризуется большим разнообразием двумерных и трехмерных изомерных форм. Среди них – изомер основного состояния Au20 (Td), представляющий собой стабильный кластер с уникальной тетраэдрической формой, в которой все атомы находятся на поверхности структуры.

Данный кластер является так называемым магическим кластером, который стабилен для определенного “магического” числа валентных электронов, когда электронные оболочки замкнуты (closed shell) в оболочечной модели нанокластеров [1–3].

Транспортные свойства электронов, определяющие электропроводимость структуры, сильно зависят от плотности состояний электронов. Энергия электронов может становиться дискретной в ряде случаев, например, при резонансном туннелировании с интерференцией электронных волн [4–6].

В работах [7, 8] было обнаружено резкое увеличение электропроводимости тонких пленок при модификации ее топологии. Принципиальным механизмом такого увеличения является наличие квантовых корреляций элементарных зарядов – электронов и дырок – в зонной структуре вблизи уровня Ферми [9].

Спектральной особенностью золотого кластера изомера Au20 является наличие чрезвычайно большого энергетического зазора электронных состояний в запрещенной зоне HOMO-LUMO (Au20), равного 1.77 эВ [9, 10], что превышает ее значение, например, для такого стабильного объекта как фуллерен (C60) примерно на 0.2 эВ, и, вероятно, является рекордной среди трехмерных металлических кластеров среднего размера.

В настоящей статье кратко рассмотрена специфика спектральных характеристик магического изомера нанокластера золота Au20 с использованием топологических моделей, что, в принципе, позволяет управлять функциональными оптическими и электрофизическими свойствами подобных структур. Для анализа используются модели на основе подхода функционала плотности состояний электронов, рассматриваемого численными методами с учетом геометрических факторов и с применением модели самосогласованного поля.

1. МЕТОД ФУНКЦИОНАЛА ПЛОТНОСТИ

Воспользуемся одним из универсальных методов – теорией функционала плотности (DFT (см., например, [11]) на основе решения уравнения Кона–Шэма, которое сводит задачу к одночастичной (одноэлектронной) проблеме с эффективным псевдопотенциалом для кластера в целом. В основном электронном состоянии такой кластер характеризуется компактной плотно упакованной тетраэдрической формой. Геометрическая модель такой структуры показана на рис. 1. С использованием указанного подхода можно определить спектральные характеристики нанокластера как многоэлектронной системы с помощью функционалов пространственно-зависимой электронной плотности.

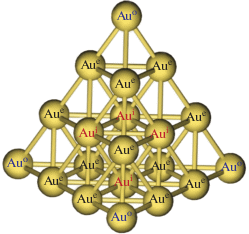
Рис. 1.

Геометрическая структура кластера тетраэдального нанокластера Au20. Представление выполнено в формате программы BURAI. Пояснения приводятся в тексте.

В основе используемой теории лежат модель Томаса–Ферми и теорема Хоэнберга–Кона [12], когда все свойства электронной структуры системы в невырожденном, основном, состоянии определяются ее электронной плотностью. Таким образом, энергию основного состояния системы можно представить в виде однозначного функционала, который зависит от плотности частиц n(r), а универсальный функционал полной системы E[n] выражается через плотность взаимодействующих частиц.

Самосогласованное одноэлектронное уравнение Шрёдингера с эффективным потенциалом Кона–Шэма, которое также известно как нестационарное уравнение Кона–Шэма для волновой функции ψ [13], имеет вид:

(1)
$i\hbar \frac{{\partial \psi }}{{\partial t}} = \left[ { - \frac{{{{\hbar }^{2}}}}{{2m}}{{\nabla }^{2}} + {{V}_{{KS}}}\left( {r,t} \right)} \right]\psi ,$
(2)
${{V}_{{KS}}}\left[ n \right]\left( {r,t} \right) = {{V}_{H}}\left[ n \right]\left( {r,t} \right) + {{V}_{{XC}}}\left[ n \right]\left( {r,t} \right) + {{V}_{{nucl}}}\left( r \right),$
где VKS – это псевдопотенциал Кона–Шэма. Он состоит из потенциала ядра ${{V}_{{nucl}}}\left( r \right),$ обменно-корреляционного (химического) потенциала ${{V}_{{XC}}}$ и потенциала Хартри–Фока ${{V}_{H}},$ описывающего его электрон-электронное кулоновское отталкивание, m – масса электрона.

Здесь мы ввели электронную плотность в виде:

(3)
$n\left( {r,t} \right) = \sum\limits_{i = 1}^{{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}} {{{{\left| {{{\psi }_{i}}\left( {r,t} \right)} \right|}}^{2}}} ,$
где произведение на 2 обозначают вырождение по спину.

В результате минимизации полной энергии системы по электронной плотности, определяемой, как сумма кинетической энергии, потенциальной энергии во внешнем поле, энергии кулоновского (хартриевского) межэлектронного взаимодействия и обменно-корреляционной энергии, получаем систему стационарных самосогласованных уравнений Кона–Шэма на основе соотношений (1)–(3):

(4)
$\left[ { - \frac{{{{\hbar }^{2}}}}{{2m}}\Delta + {{V}_{{eff}}}\left( r \right)} \right]{{\phi }_{i}}\left( r \right) = {{\varepsilon }_{i}}{{\phi }_{i}}\left( r \right),$
где εi – энергия электрона в состоянии с волновой функцией ϕi(r), и определяем стационарное состояние системы ${{\psi }_{i}}\left( {r,t} \right) = {{\phi }_{i}}\left( r \right){{e}^{{ - i{{{\varepsilon }}_{i}}t/\hbar }}}.$

В этом случае псевдопотенциал Кона–Шэма определяется следующим образом:

(5)
${{V}_{{eff}}}\left( r \right) = q_{e}^{2}\int {\frac{{n\left( {r{\kern 1pt} '} \right)dr{\kern 1pt} '}}{{\left| {r - r{\kern 1pt} '} \right|}}} + {{V}_{{XC}}}\left( r \right),$

а плотность энергетических состояний электронной системы (заряд qe) представляет сумму плотности волновых функций каждого электрона на орбитали в стационарном состоянии с учетом вырождения по спину

(6)
$n\left( r \right) = 2\sum\limits_{i = 1}^{{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0em} 2}} {{{{\left| {{{\phi }_{i}}\left( r \right)} \right|}}^{2}}} .$

Обменно-корреляционный потенциал определяется как изменение энергии на одну частицу, т.е. является химическим потенциалом:

(7)
${{V}_{{XC}}}\left( r \right) = \frac{{\delta {{E}_{{XC}}}\left[ {n\left( r \right)} \right]}}{{\delta n\left( r \right)}}.$

Энергия системы EXC в приближении локальной плотности (LDA) определяется как [14]:

(8)
${{E}_{{XC}}}\left[ n \right] = \int {{{\varepsilon }_{{XC}}}[n\left( {r{\kern 1pt} '} \right)]n\left( {r{\kern 1pt} '} \right)dr{\kern 1pt} '} ,$
где ${{\varepsilon }_{{XC}}}$ – обменно-корреляционная энергия, приходящаяся на одну частицу в однородном электронном газе с плотностью $n\left( r \right).$

Таким образом, обменно-корреляционный потенциал представляется в виде:

(9)
${{V}_{{XC}}}\left( r \right) = \frac{{d\left\{ {{{\varepsilon }_{{XC}}}\left[ {n\left( {r{\kern 1pt} '} \right)} \right]n\left( {r{\kern 1pt} '} \right)} \right\}}}{{dn\left( r \right)}} = {{\mu }_{{XC}}}\left[ {n\left( r \right)} \right],$
где ${{\mu }_{{XC}}}$ – обменно-корреляционный вклад в химический потенциал системы.

Тогда полная энергия системы E в рамках рассматриваемого формализма Кона–Шэма определяется следующим образом:

(10)
$\begin{gathered} E = \sum {{{\varepsilon }_{i}}} + \frac{{{{q}_{e}}^{2}}}{2}\int {\frac{{n\left( r \right)n\left( {r{\kern 1pt} '} \right)drdr{\kern 1pt} '}}{{\left| {r - r{\kern 1pt} '} \right|}}} + \\ + \,\,\int {n\left( {r{\kern 1pt} '} \right)} \left\{ {{{\varepsilon }_{{XC}}}\left[ {n\left( {r{\kern 1pt} '} \right)} \right] - {{\mu }_{{XC}}}\left[ {n\left( {r{\kern 1pt} '} \right)} \right]} \right\}dr{\kern 1pt} '. \\ \end{gathered} $

Результаты численного моделирования данной задачи, полученные с использованием метода самосогласованного поля с учетом плотности электронных состояний, приведены в следующем разделе.

2. ПРОЦЕДУРА МОДЕЛИРОВАНИЯ И РЕЗУЛЬТАТЫ РАСЧЕТА

Численное моделирование выполняли с помощью кодов QuantumEspresso [15]. Они представляют собой интегрированный набор компьютерных кодов в открытом доступе, используемых для расчета электронной структуры и моделирования свойств материалов на наноуровне. Данный подход основан на теории функционала плотности при разложении по плоским волнам с учетом соответствующих псевдопотенциалов (см., например, [16]). При этом псевдопотенциал или эффективный потенциал Veff используется в качестве приближения для упрощенного описания сложных систем. Для расчета был использован релятивистский PAW псевдопотенциал атома золота Au.rel-pbe-n-kjpaw_psl.1.0.0.UPF [17].

2.1. Учет геометрических параметров

Рассматриваемый наноклаcтер Au20 обладает тетраэдральной формой (Td) [10]. Такой правильный тетраэдр имеет 12 вращательных симметрий, то есть симметрий, сохраняющих ориентацию, и порядка 24 симметрий, включающих комбинацию отражений и вращений. Расчеты по релятивистскому функционалу плотности предсказывают, что Au20 обладает тетраэдрической геометрией, подобной геометрии фрагмента объемного гранецентрированного кубического (ГЦК) кристалла золота. Его четыре треугольные грани или поверхности напоминают на наноуровне ГЦК (111)-упаковку, которая присуща объемному образцу золота. Данный кластер имеет очень большую площадь поверхности, так как все атомы находятся, во-первых, на поверхности кластера, и, во-вторых, значительная доля угловых участков имеет низкое значение координационного числа. Будем различать три вида размещения атомов в структуре Td: 4 – на вершинах, 4 – в центре каждой грани и 12 – вдоль краев. Они имеют разные координационные числа и могут обеспечивать идеальные участки поверхности для связывания разных молекул, например, при катализе. Геометрическая структура данного кластера в рамках рассматриваемой модели приведена на рис. 1.

Как видно, имеющиеся 20 атомов золота Au20 (Td), подразделяются на следующие классы: четыре атома Au° с координационной вершиной, отмеченные на рисунке синим цветом; их заряд NBO, qNBO(Au°) = –0.13 и заряд Милликена qM(Au°) = –0.42; двенадцать 6-координационных краевых атомов Аue, отмеченных на рисунке черным цветом, с зарядом qNBO(Aue) = –0.02 и qM(Aue) = –0.09; четыре 9-координационных внутренних или гранецентрированных атомов Aui, отмеченных на рисунке красным цветом, с зарядом qNBO(Aui) = 0.06 и qM(Aui) = –0.15. При этом вводятся натуральные связевые орбитали (NBO), которые характеризуют распределение электронной плотности в молекуле и/или нанокластере [18]. Они представляют собой ортонормированный набор локализованных орбиталей с “максимальной занятостью”, чьи ведущие N/2 члены (или N членов в случае с открытой оболочкой) дают наиболее точное из возможных Льюис-подобных описаний полной плотности N-электронов. Расстояния между атомами в кластере – порядка 2.85 Å.

2.2. Модель самосогласованного поля

Воспользуемся моделью самосогласованного поля – SCF (self-сonsistent field), используемой для вычислений в теории функционала плотности Кона–Шэма [19]. В данном методе на основе итерационного подхода подбираются такие значения входных данных, при которых оператор Кона–Шэма имеет решение, удовлетворяющее исходному уравнению Шрёдингера. Для проведения вычислений необходимо задать начальное значение плотности ${{n}_{0}};$ далее строится Гамильтониан Кона–Шэма с эффективным потенциалом (5):

(11)
${{H}_{{KS}}}\left[ {{{n}_{0}}\left( r \right)} \right] = - \frac{1}{2}{{\nabla }^{2}} + {{V}_{{eff}}}\left[ {{{n}_{0}}\left( r \right)} \right]\left( r \right).$

Решение уравнения Кона–Шэма на собственные значения εi находится из соотношения:

(12)
${{H}_{{KS}}}\left[ {{{n}_{0}}\left( r \right)} \right]{{\phi }_{i}}\left( r \right) = {{\varepsilon }_{i}}{{\phi }_{i}}\left( r \right).$

После этого рассчитывается плотность n согласно (3), которая сравнивается с начальной плотностью. В случае отличных ее значений от исходной плотности реализуется вариация начальной электронной плотности на каждом шаге итерации по критерию, чтобы расчетная плотность сходилась к начальному значению n0. Эта процедура проводится до тех пор, пока ошибка в выборе начальной плотности не будет минимально допустимой или заданной. Таким образом, если ${{n}_{0}} = n,$ то это значит, что решение получено, верно; если ${{n}_{0}} \ne n,$ то подбирается другое значение начальной плотности.

По результатам проделанных вычислений построен график зависимости полной энергии в относительных единицах ширины одной полосы Ферми–Дирака в единицах постоянной Ридберга – Ry) от числа итераций (рис. 2).

Рис. 2.

График сходимости в модели самосогласованного поля, построенный с использованием программы QuantumEspresso (BURAI). Процедура описана в тексте.

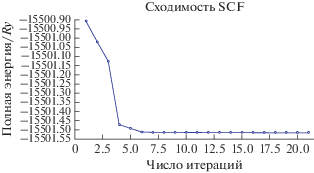
При расчете были получены следующие численные параметры системы: значение полной энергии для данного кластера равно –15501.514·Ry; число итераций соответствовало 21; отсечка кинетической энергии происходила по уровню 40.0000 · Ry; отсечка плотности заряда – по уровню 450.000 · Ry.

При этом полная энергия складывается из следующих компонент: одноэлектронный вклад равен –2374.301 · Ry; вклад Хартри равен 1362.743 · Ry; обменная энергия равна –640.386 · Ry; вклад Эвальда равен 0.645 · Ry; одноцентровой вклад равен –13850.202 · Ry.

2.3. Спектральные характеристики

Для вычисления электронного спектра нанокластера воспользуемся данными для значений энергии для каждой орбитали Au20, вычисленными в выходных файлах программой Quantum Espresso. Для визуализации энергетических уровней была использована программа, написанная на языке Python для чтения выходных данных.

Полученный спектр рассматриваемого нанокластера представлен на рис. 3. В соответствии с результатами предыдущего пункта уровень энергии Ферми Ef = –0.8049 эВ. Для наглядной визуализации этот уровень выбран условно как нулевой, а остальные линии смещены относительно его значения. Ниже уровня Ферми, самый верхний уровень валентной зоны есть HOMO-орбиталь, а выше уровня Ферми частично заполнен только самый нижний уровень зоны проводимости – LUMO-орбиталь [9]. Согласно рассчитанному спектру, значение энергии орбитали HOMO равно –0.4726 эВ, а значение энергии орбитали LUMO – 1.2831 эВ. Отсюда можно вычислить значение величины межзонной щели (запрещенной зоны) – 1.7557 эВ, что близко к известному экспериментальному значению, равному 1.77 эВ [10].

Рис. 3.

Полученный спектр нанокластера изомера Au20. Пунктирной линией отмечен уровень Ферми, рассчитанный с помощью программы Python. Условия расчета: число электронов N в данной системе равно 220; число состояний Кона–Шэма – 130.

Таким образом, используемая модель позволяет полностью описать вид спектра, распределение спектрального веса между нижней (хаббардовской) зоной и резонансным пиком на вершине валентной зоны.

2.4. Плотность состояний

Принципиальным параметром атомной (кластерной) системы является плотность состояний (density of states, DOS), т.е. число собственных состояний, определяемых уравнением Шредингера на единицу энергии и единицу объема.

Результаты моделирования показаны на рис. 4. Полученные зависимости позволяют сделать ряд выводов о зонной структуре исследуемого кластера. Как было показано в предыдущем пункте, значение энергии межзонной щели равно 1.7557 эВ. Данное значение соответствует полученному графику плотности состояний.

Рис. 4.

Распределение плотности электронных состояний для нанокластера Au20, построенное с использованием программы QuantumEspresso (BURAI). На приведенном графике состояния со спином вверх представлены верхней кривой, а состояния со спином вниз – нижней.

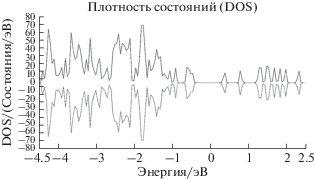
Область ниже нулевого значения, то есть находящаяся ниже уровня Ферми, является широкой “валентной” зоной с характерными пиками на уровнях значений энергии: –1.8, –2.1, –2.4, –3.17, –3.65 и –4.23 эВ. Потолок данной зоны, то есть HOMO-орбиталь, соответствует пику на графике со значением энергии –0.4726 эВ.

Область на графике выше нулевого значения является зоной “проводимости”; дно этой энергетической зоны, то есть орбиталь LUMO, соответствует пику со значением энергии, равным 1.2831 эВ. Из графика можно сделать вывод, что изомер нанокластера золота Au20, действительно, обладает широким энергетическим зазором между отмеченными зонами. Это факт имеет решающее значение не только для оптических свойств, но и для электропроводимости. Особенно это важно при анализе возможности реализации сверхпроводимости в подобной топологической гранулированной системе [5, 9, 20].

2.5. Оптические свойства

Рассмотрим особенности полученного расчетного спектра состояний, представленного на рис. 4. Причиной большого значения щели LUMO-HOMO – величины запрещенной зоны, могут служить следующие факторы. Во-первых, стабильность кластера, так как это магический кластер с полностью заполненной оболочкой. Также стоит отметить наличие релятивистских эффектов, которые существенно стабилизируют 6s атомные орбитали. Во-вторых, уникальная тетраэдральная высокосимметричная структура, каждый атом в которой находится на поверхности. В-третьих, эффект ароматичности, характеризующийся наличием аморфно-подобных структур, отсутствующих в других кластерных металлических системах.

Кроме того, нанокластер Au20 (Td) может проявлять некоторые специфические оптические свойства в видимом диапазоне, особенно нелинейного характера, вследствие его тетраэдральной симметрии. При этом перенос заряда между ребрами и вершинами вносит значительный вклад в нелинейно оптический отклик. В работе [21] продемонстрирована существенная молекулярно-оптическая нелинейность второго порядка, которая отражается в статистической гиперполяризуемости ${{{\beta }}_{{xyz}}}$ кластера первого порядка и ее величина определяется значением ${{{\beta }}_{{xyz}}}$ = 1.521. Пик самой низкой величины энергии связан с зазором, который отделяет основное синглетное состояние Au20 (Td) от первого возбужденного триплетного состояния, величина которого экспериментально оценивается как 1.77 эВ. При этом явно выраженные пики с энергиями 2.2, 2.7, 3.1 эВ и большой энергетической щелью соответствуют переходам при более высоких энергиях связи.

Основная причина образования большой величины зазора между HOMO и LUMO оболочками связана с гибридизацией валентных уровней 5d и 6s атома золота, вызывающих перекрытие 5d оболочек соседних атомов в кластере.

В наших расчетах не учтено спин-орбитальное взаимодействие, и считается, что промежуточные состояния в запрещенной зоне не заполнены. Вследствие этого на графике можно видеть 2 пика, расположенных в запрещенной зоне. Для выяснения причин их появления требуются дополнительные исследования и подробное, более детальное, изучение плотности состояний с учетом спин-орбитального взаимодействия.

Варьирование в заданном направлении всех перечисленных выше факторов (внешнее воздействие, модификация граничных условий на подложке и других параметров) позволяет управлять оптическими характеристиками таких структур, что особенно принципиально для реализации возникающих энергетических пиков. Это дает возможность контролировать функциональные свойства оптических систем на основе подобных структур. Хотя данный вопрос требует отдельного рассмотрения, но физическая концепция такого влияния вполне очевидна и может быть обоснована в конкретных условиях для реального эксперимента.

ЗАКЛЮЧЕНИЕ

В данной работе методом функционала плотности было проведено исследование изомера нанокластера Au20 с уникальной тетраэдральной структурой, и были получены электронная диаграмма и картина плотности электронных состояний, а также значения энергии для уровней HOMO-LUMO, и значение энергии межзонного зазора между ними.

Продемонстрировано, что энергетическая структура нанокластера существенным образом зависит от геометрии изомера (и определяется его симметрией в данном случае – Td). Рассмотренный изомер нанокластер золота Au20 (Td) обладает большим энергетическим зазором и двумя выраженными пиками в запрещенной зоне. Физический смысл последнего факта, вероятно, связан с расщеплением LUMO орбитали на три подуровня, однако это утверждение требует дальнейшего анализа и верификации аналогично [10], а также учета спин-орбитального взаимодействия [12].

Проведенный численный анализ спектральных характеристик изомера “магического” нанокластера золота Au20 показывает возможность управления такими важными характеристиками как ширина запрещенной зоны и плотность электронных энергетических состояний за счет изменение геометрии структуры. Спектральные электронные характеристики нанокластера в конечном итоге определяют функциональные оптические и электрофизические свойства образцов с изомерами золота. Они имеют несомненные перспективы для различных приложений, использующих как новые физические принципы для создания тонкопленочных элементов фотоники разного предназначения, так и в аспекте исключительной роли этих явлений в фундаментальных исследованиях с использованием подобных систем. Речь идет, в частности, об эффектах сверхпроводимости чувствительных к структуре электронных энергетических уровней вблизи запрещенной зоны (см., например, [9]).

Действительно, для проблемы высокотемпературной сверхпроводимости обсуждаются новые механизмы образования связанных электронов (Куперовских пар), но не за счет стандартного фононного механизма (см., например, [22]), а из-за топологических особенностей используемых структур по аналогии с топологическими изоляторами [2]. Развитие этих подходов – предмет дальнейших исследований. Принципиальным при этом является анализ возможности достижения сверхпроводящих топологических состояний благодаря оптимальному выбору соответствующего элементного состава для таких структур, хотя в настоящей работе мы кратко обсудили, как первый этап, только простые комбинации элементов из атомов золота [23].

Таким образом, применение используемых подходов к анализу оптических свойств материалов, перспективных по элементному составу, например, к достижению высокотемпературной сверхпроводимости, имеет и очевидный прикладной аспект и позволит выявить тенденции и тренды к получению реальных систем с такими уникальными электропроводящими характеристиками на практике.

Исследование выполнено при финансовой поддержке РФФИ (проект № 20-02-00515) и в рамках выполнения государственного задания ВлГУ в сфере научной деятельности № 0635-2020-0013.

Список литературы

  1. Гантмахер В.Ф. Электроны в неупорядоченных средах. М.: Физматлит, 2013. 288 с.

  2. Аракелян С.М., Кучерик А.О., Прокошев В.Г. и др. Введение в фемтонанофотонику. Фундаментальные принципы и методы лазерной диагностики и управления наноструктурированными материалами. М.: Логос, 2015. 744 с.

  3. De Heer W.A. // Rev. Mod. Phys. 1993. V. 65. № 3. P. 611.

  4. Kohn W., Sham L. // J. Phys. Rev. 1965. №140. A1133.

  5. Arakelian S.M., Chestnov I.Yu., Istratov A.V. et al. // Proc. 1st Int. Nonlin. Dynamics Conf. (NODYCON 2019). V. III. Springer Nature Switzerland AG, 2020. P. 121.

  6. Аракелян С.М., Кучерик А.О., Худайберганов Т.А., Бухаров Д.Н. // Изв. РАН. Сер. физ. 2020. Т. 84. № 3. С. 322; Arakelian S.M., Kucherik A.O., Khudaiberganov T.A., Bukharov D.N. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. № 3. P. 245.

  7. Аракелян С.М., Осипов А.В., Истратов А.В. и др. // Изв. РАН. Сер. физ. 2017. Т. 81. № 12. С. 1587; Arakelian S.M., Osipov A.V., Istratov A.V., et al. // Bull. Russ. Acad. Sci. Phys. 2017. V. 81. №. 12. P. 1401.

  8. Аракелян С.М., Осипов А.В., Скрябин И.О. и др. // Изв. РАН. Сер. физ. 2017. Т. 81. № 12. С. 1604; Arakelian S.M., Osipov A.V., Skryabin I.O. et al. // Bull. Russ. Acad. Sci. Phys. 2017. V. 81. № 12. P. 1416.

  9. Кресин В.З., Овчинников Ю.Н. // УФН. 2008. Т. 178. № 5. С. 449; Kresin V.Z., Ovchinnikov Yu.N. // Phys. Usp. 2008. V. 51. № 5. P. 427.

  10. Li J., Li X., Zhai H.-J., Wang L.-S. // Science. 2003. V. 7. P. 864.

  11. Bae G.T., Aikens C.M. // J. Phys. Chem. C. 2012. V. 116. № 18. P. 10356.

  12. Ландау Л.Д., Лифшиц Е.М. Курс теоретической физики. Квантовая механика, 2004. 224 с.

  13. Burke K., Werschnik J., Gross E.K.U. // J. Chem. Phys. 2005. V. 123. № 6. Art. № 062206.

  14. Bagayoko D. // AIP Adv. 2014. V. 4. № 12. Art. № 127104.

  15. https://www.quantum-espresso.org.

  16. Энхтор Л., Силонов В.М. // Изв. РАН. Сер. физ. 2014. Т. 78. № 11. С. 1432; Enkhtor L., Silonov V.M. // Bull. Russ. Acad. Sci. Phys. 2014. V. 78. № 11. P. 1163.

  17. https://www.quantum-espresso.org/pseudopotentials/ ps-library/in.

  18. Glendening E.D., Landis C.R., Weinhold F. // Wiley Interdiscip. Rev. Comp. Molec. Sci. 2012. V. 2. № 1. P. 1.

  19. Wu K.C., Li J., Lin C.S. // Chem. Phys. Lett. 2004. V. 388. № 4–6. P. 353.

  20. Аракелян С.М., Худайберганов Т.А., Истратов А.В. и др. // Опт. и спектроск. 2019. Т. 127. № 7. С. 125; Arakelian S.M., Khudaberganov T.A., Istratov A.V. et al. // Opt. Spectrosс. 2019. V. 127. № 7. P. 121.

  21. Szabo A., Ostlund N.S. Modern quantum chemistry. Mineola, New York: Dover Publ., 1996. 480 p.

  22. Абрикосов А.А. Основы теории металлов: уч. пособ. М.: Физматлит, 2010. 599 с.

  23. Arakelian S.M., Kucherik A.O., Khudaberganov T.A. et al. // Opt. Quant. Electron. 2020. V. 52. № 4. P. 202.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал