Известия РАН. Серия физическая, 2020, T. 84, № 2, стр. 289-294

ВВЕДЕНИЕ

На сегодняшний день одним из наиболее перспективных методов мониторинга мирового океана является акустическая томография [1]. Она позволяет получить информацию о пространственных распределениях различных характеристик акваторий с размерами, достигающими сотен и тысяч километров. В настоящей работе рассматривается решение задачи модовой томографии океана на основе функционально-аналитического алгоритма Новикова–Сантацесариа [2], изначально разработанного для задач рассеяния в квантовой механике. Данный подход не требует ни линеаризации модели и построения матриц возмущений, ни итераций и привлечения дополнительных процедур регуляризации, что выгодно отличает его от использующихся в настоящее время методов, а также делает перспективным исследование его возможностей в задачах акустической томографии океана. Для исследования возможностей этого алгоритма в акустических приложениях потребовалось решить прямую задачу – найти акустическое поле при заданных параметрах рассеивателя с учетом неадиабатического рассеяния мод.

РЕШЕНИЕ ПРЯМОЙ ЗАДАЧИ АКУСТИЧЕСКОГО РАССЕЯНИЯ С УЧЕТОМ ВЗАИМОДЕЙСТВИЯ МОД

В качестве фонового волновода рассматривается волновод с абсолютно жестким дном, свободной верхней границей и однородным в горизонтальной плоскости водным слоем. В случае присутствия неоднородности скорости звука, уравнение Гельмгольца, описывающее распространение акустических волн, имеет вид:

где $\vec {r} = \{ x,y,z\} $ – радиус-вектор в выбранной системе координат; $v(\vec {r},{{\omega }_{j}}) = \omega _{j}^{2}\left( {\frac{1}{{c_{0}^{2}(z)}} - \frac{1}{{{{c}^{2}}(\vec {r})}}} \right)$ – функция рассеивателя, описывающая отклонение фазовой скорости $c(\vec {r})$ от ее фонового значения ${{с}_{0}}(\vec {r}) \equiv {{с}_{0}}(z);$ индекс $j$ подразумевает возможность использования широкополосного режима зондирования (далее частотная зависимоть будет опущена для достижения компактности выражений); ${{k}_{0}} = \frac{{{{\omega }_{j}}}}{{{{c}_{0}}(z)}}.$ Решение уравнения (1) ищем в виде суммы мод $p(\vec {r})$ = $\sum\nolimits_{n = 0}^\infty {{{\Phi }_{n}}(x,y){{\Psi }_{n}}(z)} ,$ где ${{\Phi }_{n}}(x,y)$ описывает решение уравнения Гельмгольца в горизонтальной плоскости $(x,y),$ а $\Psi _{n}^{{}}(z)$ – вертикальный профиль моды номера $n$ в фоновом волноводе: здесь $k_{{0n}}^{2}$ – горизонтальное волновое число $n$-ой моды в невозмущенном волноводе, а $H$ – глубина волновода.

С учетом условия ортогональности профилей мод $\int_0^H {{{\Psi }_{m}}(z){{\Psi }_{n}}(z)dz} = {{\delta }_{{mn}}},$ где ${{\delta }_{{mn}}} = \left\{ {\begin{array}{*{20}{c}} {1,m = n} \\ {0,m \ne n} \end{array}} \right.$ – символ Кронекера, уравнение (1) переписывается в виде:

где оператор ${{S}_{{mn}}}(x,y)$ ≡ $\int_0^H {{{\Psi }_{m}}(z)v(x,y,z){{\Psi }_{n}}(z)dz} $ описывает модовое взаимодействие. Решение прямой задачи основывается на сведении (3) к уравнению типа Липпмана–Швигнера [3] и последующем его решении с помощью дискретизации задачи. Для этого вводится функция Грина ${{G}_{{0m}}}(x,y,{{k}_{{0m}}})$ моды номера $m$ однородной изотропной непоглощающей среды:

Использование ${{G}_{{0m}}}(x,y,{{k}_{{0m}}})$ позволяет перейти от (3) к связанной системе уравнений типа Липпмана–Швигнера:

где $\Re $ – область, в которой локализован оператор ${{S}_{{mn}}}(x,y).$ Перепишем (5) в матричном виде: где $\hat {E}$ – единичная матрица. На основе (6), зная функцию рассеивателя и невозмущенные значения поля, рассчитываем поля, рассеянные на заданной неоднородности $v(x,y,z).$ Рассматриваемый функционально-аналитический алгоритм [2], а также результаты работы [4] позволяют на основе анализа рассеянных полей ${{\Phi }_{m}}(x,y)$ оценить значения оператора ${{S}_{{mn}}}.$

ФУНКЦИОНАЛЬНОЕ РЕШЕНИЕ ЗАДАЧИ МОДОВОЙ ТОМОГРАФИИ ОКЕАНА

Исходной, при решении обратной задачи, будет являться система связанных уравнений Гельмгольца (3):

В адиабатическом приближении, когда передачи энергии между модами разных номеров не происходит, система (7) распадается на $n$ независимых двумерных уравнений:

Ставится вопрос о нахождении значений матричного оператора ${{S}_{{nn}}}$ для каждой n-ой моды, т.е. требуется решить набор двумерных обратных задач восстановления ${{S}_{{nn}}}$ по данным в виде рассеянных полей отдельных мод. В [5] был численно реализован двумерный функционально-аналитический алгоритм Новикова, позволяющий по данным в виде амплитуд рассеяния, описывающих поля квазиточечного источника в дальней зоне, восстановить двумерную функцию рассеивателя. Эти результаты были использованы в настоящей работе для восстановления двумерного оператора ${{S}_{{nn}}}(x,y),$ который, в свою очередь, содержит в себе данные о функции рассеивателя $v(\vec {r}).$ Для этого, на первом шаге требовалось перейти от ${{\Phi }_{n}}(x,y)$ к обобщенной амплитуде рассеяния.

Как было показано в работе [4], с помощью рассматриваемого функционально аналитического алгоритма можно, на основе строгих интегральных преобразований, перейти от классической функции Грина ${{G}^{{cl}}}(x,y;\omega )$ к обобщенной амплитуде рассеяния ${{h}^{ \pm }}(\vec {k},\vec {l};\omega ),$ где $\vec {k}$ и $\vec {l}$ это волновые векторы падающей и рассеянной волны соответственно. Основной идеей алгоритма является представление волнового вектора в виде комплексной величины $\vec {k} = {{\vec {k}}_{R}} + i{{\vec {k}}_{I}}$ при выполнении условия монохроматичности: ${{\vec {k}}^{2}} = {{\vec {l}}^{2}} = {{\left( {\frac{\omega }{{{{c}_{0}}}}} \right)}^{2}}.$ К волновому вектору добавляется бесконечно малая ортогональная составляющая, а верхний индекс ± обобщенной амплитуды рассеяния отвечает двум возможным ориентациям этой добавки в пространстве – правосторонней и левосторонней. В нашей задаче ${{\Phi }_{n}}(x,y)$ будет являться классической функцией Грина для моды номера $n.$

Для учета модового взаимодействия в обратной задаче вводим вспомогательный оператор ${{V}_{{mn}}}(x,y)$ = $\left[ {k_{0}^{2} - k_{{0m}}^{2}} \right]{{\delta }_{{mn}}} + {{S}_{{mn}}}(x,y),$ который приводит систему (7) к следующему виду:

Решение данной системы уравнений для ${{k}_{0}}(x,y,z) = {{k}_{0}} \equiv {\text{const}}$ реализуется с помощью алгоритма Новикова–Сантацесариа [2]. По-видимому, первые результаты численного моделирования схемы акустической томографии океана, основанной на алгоритме Новикова–Сантацесариа и учитывающей неадиабатические эффекты, были представлены в [6]. Однако в [6] не удалось перейти к восстановлению трехмерных рассеивателей $v(x,y,z)$ по данным в виде набора двумерных операторов ${{S}_{{nn}}}(x,y).$

ИСПОЛЬЗОВАНИЕ ФУНКЦИЙ КАРУНЕНА–ЛОЭВА ДЛЯ ВОССТАНОВЛЕНИЯ ТРЕХМЕРНЫХ РАССЕИВАТЕЛЕЙ

Для восстановления трехмерных рассеивателей ${v}(x,y,z)$ в адиабатическом приближении необходимо для каждого узла пространственной сетки $(x,y)$ решить интегральное уравнение вида:

Пусть число распространяющихся мод $n = 1,...N.$ Дискретизуя задачу по $z = \{ {{z}_{1}},{{z}_{2}},...,{{z}_{I}}\} ,$ $i = 1,...I,$ $h \equiv {{z}_{1}} - {{z}_{2}},$ интегральное уравнение (10) можно свести к системе линейных алгебраических уравнений:

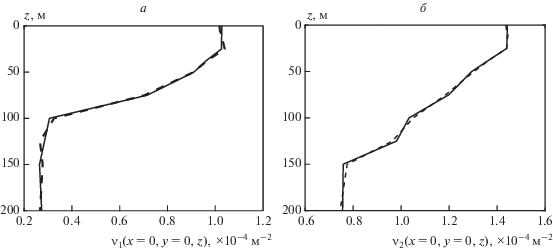
Для хорошей обусловленности матрицы $\hat {\Psi }_{{ni}}^{2}$ необходимо, чтобы число узлов пространственной сетки по оси $z$ не превышало количества распространяющихся мод: $I \leqslant N.$ Так как для характерных реальным распределениям скоростей звука в океане подынтегральная функция $\Psi _{n}^{2}(z)v(z)$ имеет характер осцилляций, частота которых растет с номером моды (рис. 1а), прямое решение системы (11) не дает удовлетворительной точности решения.

Для повышения точности восстановления на функцию рассеивателя накладывается дополнительное условие гладкости: $\frac{{v({{z}_{{i + 1}}}) - 2v({{z}_{i}}) + v({{z}_{{i - 1}}})}}{{2h}} \approx 0.$ Это позволяет, не ухудшая обусловленности матрицы $\hat {\Psi }_{{ni}}^{2},$ увеличить дискретизацию по оси $z.$ Выше на рис. 1б представлен результат восстановления амплитудного возмущения фоновой скорости звука.

Альтернативный способ решения уравнения (10), не требующий дополнительных условий гладкости, использует метод разложения функции рассеивателя по эмпирическим ортогональным функциям $v(x,y,z) = \bar {v}(z)$ + $\sum\nolimits_{j = 1}^J {{{\alpha }_{j}}(x,y){{\varphi }_{j}}(z)} ,$ где количество эмпирических ортогональных функций (функций Карунена–Лоэва) J существенно меньше количества I неизвестных $v({{z}_{i}}),$ $i = 1,..,I.$ Рассмотрим $v(x,y,z)$ как случайную величину. Если для исследуемой акватории ранее были измерены профили скоростей звука, по которым рассчитаны функции рассеивателя, то можно рассматривать набор $\{ {{v}_{b}}({{z}_{i}})\} ,$ $b = 1,...B$ как реализации данной случайной величины. Тогда, согласно теореме Карунена–Лоэва [7], собственные функции ковариационной матрицы ${{K}_{{kl}}},$ будут являться базисом, по которому единственным образом можно разложить искомую функцию рассеивателя:

где ковариационная матрица определяется следующим образом:

При этом количество базисных функций в разложении будет минимально возможным для заданной точности такого разложения.

Используя данный подход к описанию функции рассеивателя, исходное интегральное уравнение (10) можно представить в виде:

Тогда, введя новые обозначения, получим систему линейных алгебраических уравнений:

где A_nj = $\int_0^H {\Psi _{n}^{2}(z){{{\varphi }}_{j}}(z)dz} $ и ${{\tilde {S}}_{{nn}}}$ = S_nn – $\int_0^H {\Psi _{n}^{2}(z)\bar {v}(z)dz} .$

Решение системы (15) для каждой точки в плоскости $(x,y),$ позволяет оценить коэффициенты разложения ${{\hat {\alpha }}_{j}}(x,y)$ искомой функции рассеивателя по выбранному базису и, в конечном счете, оценить трехмерную функцию рассеивателя:

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

На текущем этапе проводимых исследований анализируются возможности восстановления трехмерных рассеивателей в адиабатическом приближении. Так как резкие изменения функции рассеивателя ведут к увеличению неадиабатических эффектов, то при численном моделировании встает вопрос об осуществлении плавного перехода от фонового значения ${{c}_{0}}(z)$ к возмущенному $c(z).$ Использованные при моделировании профили скоростей звука ${{c}_{0}}(z)$ и $c(z),$ представленные на рис. 3б и 3в соответственно, являются характерными для условий мелкого моря. Предполагается, что фоновый и возмущенный профили можно разложить по рассмотренным в предыдущем разделе эмпирическим ортогональным функциям ${{\psi }_{j}}(z){\text{:}}$ ${{\left. {{{c}_{0}}(x,y,z)} \right|}_{{\sqrt {{{x}^{2}} + {{y}^{2}}} > {{R}_{{inh}}}}}}$ = $\bar {c}(z)$ + + $\sum\nolimits_{j = 1}^J {{{\xi }_{j}}(x,y){{\psi }_{j}}(z)} ,$ ${{\left. {c(x,y,z)} \right|}_{{\sqrt {{{x}^{2}} + {{y}^{2}}} \leqslant {{R}_{{inh}}}}}}$ = $\bar {c}(z)$ + + $\sum\nolimits_{j = 1}^J {{{\eta }_{j}}(x,y){{\psi }_{j}}(z)} ,$ где $R_{{inh}}^{{}}$ – характерный радиус неоднородности, находящейся в центре координат, $\bar {c}(z)$ – средняя по ансамблю реализаций $\{ {{c}_{b}}(z)\} ,$ $b = 1,...B$ профилей скорость звука. В этом случае плавный переход между $c_{0}^{{}}(x,y,z)$ и $c(x,y,z)$ можно задать через переход от коэффициентов разложения $\xi _{j}^{{}}(x,y)$ к $\eta _{j}^{{}}(x,y)$ в виде цилиндра со сглаженными краями $\gamma _{j}^{{}}(x,y)$ (рис. 3а). В этом случае распределение скорости звука во всех точках акватории будет задаваться в виде $c(x,y,z)$ = = $\Gamma (x,y)\left\{ {\bar {c}(z) + \sum\nolimits_{j = 1}^J {{{\gamma }_{j}}(x,y){{\psi }_{j}}(z)} } \right\},$ где $\Gamma (x,y)$ – амплитудный коэффициент, также имеющий вид сглаженного цилиндра, но к которому добавлены экспоненциальные возмущения, с помощью которых можно оценить разрешающую способность алгоритма. Изменение модуля коэффициента $\Gamma (x,y)$ позволяет варьировать силу рассеивателя.

При численном моделировании были использованы следующие параметры модели: $f = 20$ Гц – частота излучателей, $R_{{tomo}}^{{}} = 546$ м – радиус области томографирования, $q = 60$ – количество источников-приемников, $H = 200$ м – глубина акватории, $N = 5$ – число рассматриваемых мод, ${{c}_{{00}}} = 1457$ м/с – средняя фоновая скорость звука, $\frac{{{{c}_{{00}}}}}{{5f}} = 14.57$ м – шаг пространственной дискретизации в плоскости $(x,y),$ $R_{{inh}}^{{}} = 256$ м – характерный радиус неоднородности, $\frac{{\max \Gamma (x,y)}}{{{{с}_{{00}}}}}$ = = 6.9% – относительный контраст неоднородности. Набеги фазы первой и пятой моды для исследуемого рассеивателя (рис. 4а) соответственно равны $\Delta {{\varphi }_{{n = 1}}} \approx 0.95\pi $ и $\Delta {{\varphi }_{{n = 5}}} \approx 2.85\pi .$

ЗАКЛЮЧЕНИЕ

Применение строгих функционально-аналитических методов в акустических приложениях позволяет рассматривать задачи, которые в настоящее время не имеют решения, но представляют бесспорный практический интерес. Примером такого рода задач является неадиабатическая модовая томография неоднородного движущегося океана. В настоящей работе получены результаты, позволяющие продвинуться в решении этой задачи. Предложенная в работе схема акустической томографии океана, основанная на алгоритме Новикова–Сантацесариа, позволяет восстанавливать трехмерные рассеиватели $v(x,y,z)$ из наборов значений двумерных операторов ${{S}_{{nn}}}(x,y)$ с привлечением функций Карунена–Лоэва. Такой подход обладает новизной, поскольку ранее не рассматривался. При этом, в отличие от [8], для восстановления трехмерных неоднородностей функциональными алгоритмами дополнительных итераций не требуется. Дальнейшая работа в данном направлении представляется весьма перспективной.

Работа выполнена при финансовой поддержке грантами РФФИ (проект № 17-51-150001 НЦНИ_а) и Президента РФ для государственной поддержки ведущих научных школ № НШ 5545.2018.5.