Известия РАН. Серия физическая, 2020, T. 84, № 3, стр. 451-456

ВВЕДЕНИЕ

Для исследования синхронизации релаксационных автоколебаний с решениями, содержащими фазы медленного и быстрого изменения переменных, используются нелинейные дифференциальные уравнения с малым параметром при старших производных [1, 2]

где $\bar {x} = ({{x}_{1}},...,{{x}_{k}}),$ $\bar {y} = ({{y}_{1}},...,{{y}_{l}}),$ $\bar {f} = ({{f}_{1}},...,{{f}_{k}}),$ $\bar {g} = ({{g}_{1}},...,{{g}_{l}}),$ ${{\bar {\beta }}_{1}}(t),$ ${{\bar {\beta }}_{2}}{\text{(}}t)$ – синхронизирующее воздействие. Фазовое пространство ${{R}^{n}}$ $(n = k + l)$ системы (1) естественно распадается в прямую сумму k-мерного подпространства ${{X}^{k}}$ и $l$ – мерного подпространства ${{Y}^{l}}.$ Для фазовой картины (1) характерно наличие “быстрых” и “медленных” движений. Если в результате чередования медленных и быстрых движений возникнет замкнутая траектория тогда соответствующее ей периодическое решение (1) представляет релаксационное колебание. Установлено, что управление релаксационными колебаниями может быть достигнуто за счет управления отдельными фазами колебания наиболее эффективно медленными [1–3]. При экспериментальной реализации режимов синхронизации были использованы импульсные внешние воздействия: периодическое с периодом ${{T}_{c}}$ и периодические релаксационные автоколебания.

МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СИНХРОНИЗАЦИИ, ИСПОЛЬЗУЮЩАЯ МЕТОДЫ РАВНОМЕРНЫХ ПОЧТИ-ПЕРИОДИЧЕСКИХ ФУНКЦИЙ

В 1989 г. был предложен прямой метод описания синхронизации релаксационных систем, использующий методы теории равномерных почти-периодических функций и основанный на неравенствах Кронекера [2–6]. В этом методе аксиоматически задается форма релаксационного колебания и пороговая функция, описывающая рефрактерность релаксационного осциллятора – динамический порог возбуждения. В этих работах с помощью методов теории равномерных почти-периодических функций и неравенств Кронекера было показано, что для исследования основных режимов синхронизации типа ${m \mathord{\left/ {\vphantom {m n}} \right. \kern-0em} n}$ и определения амплитудно-частотных характеристик стационарной синхронизации релаксационных осцилляторов могут быть использованы соотношения-неравенства Кронекера

где ${{T}_{1}},$ ${{T}_{2}}$ – периоды синхронизирующего сигнала и релаксационного осциллятора, ${\varepsilon } = {{f}^{{ - 1}}}(U);$ $f(T)$ – пороговая чувствительность в фазу относительной рефрактерности. Для описания переходных процессов, предшествующих стационарной синхронизации, могут быть использованы соотношения, включающие неоднородные неравенства Кронекера

В теории чисел неравенство (3) известно как неравенство Чебышева, все возможные решения его неизвестны до настоящего времени [7]. В данной работе рассматриваются аналитическая и численная компьютерная реализации предлагаемого метода.

СИНХРОНИЗАЦИЯ НЕЙРОННЫХ АНСАМБЛЕЙ ПРИ ФОРМИРОВАНИИ ВНИМАНИЯ

Рассмотрим задачу формирования процесса внимания при синхронизации нейронного ансамбля от центрального нейрона-автогенератора. Эта задача имеет большое прикладное значение для понимания механизма когнитивных процессов [8–18]. Элементами первого слоя являются периферические нейроны (ПН). Они представляют собой детекторы признаков в первичных зонах новой коры, активируемые внешними стимулами. Вообще говоря, ПН должны быть связаны возбуждающими латеральными связями, но для упрощения модели в данной работе эти связи элиминированы так, что все взаимодействие между ПН идет через центральный управляющий элемент ЦН. Центральный управляющий элемент представлен предельно упрощенно и состоит из двух групп нейронов, ЦН1 и ЦН2. ЦН1 используется для синхронизации некоторого ансамбля ПН. Зрительный объект, представленный ансамблем ПН, работающим синфазно с ЦН1, считается включенным в когнитивный процесс. ЦН2 управляет последовательной синхронизацией ЦН1 с разными ансамблями ПН, что интерпретируется как последовательный выбор разных объектов внимания.

ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ ДЛЯ ИССЛЕДОВАНИЯ СИНХРОНИЗАЦИИ РЕЛАКСАЦИОННЫХ АВТОКОЛЕБАНИЙ ПРИ ФОРМИРОВАНИИ ВНИМАНИЯ

Аксиоматическая модель релаксационной автоколебательной системы задается в виде двух различных функций на двух последовательных временных участках [2–6].

где $f(t)$ – функция, характеризующая форму релаксационного автоколебания; ${{f}_{1}}(t),$ ${{f}_{2}}(t)$ – функции, характеризующие релаксационное автоколебание в интервале “быстрого” и “медленного” изменения релаксационного автоколебания; ${{f}_{3}}(t)$ – функция, характеризующая динамический порог возбуждения в интервале “медленной” фазы. Качественная аппроксимация функций $f(t)$ и ${{f}_{\partial }}(t)$ для типового нейрона показана на рис. 1.

Вычислительный алгоритм реализует формулы (4). При численной реализации выделение ε‑почти-периодов равномерной почти-периодической функции, получаемой в результате синхронизации, осуществляется путем выделения остатка R от деления текущего времени процесса на период синхронизирующего колебания с помощью встроенной процедуры языка MathLab 7 $R = \bmod \frac{t}{{{{T}_{c}}}} = \bmod \frac{{n\Delta t}}{{{{T}_{c}}}},$ где: $t$ – текущее время, Δt – шаг вычислений по времени, n – число шагов. Остаток R равен аргументу алгебраической аппроксимации двух функций “быстрой” и “медленной” фазы релаксационного колебания и динамического порога возбуждения, соответствующего “медленной” фазе движения. Далее используется условие, описывающее внеочередное возбуждение релаксационного автоколебания при превышении динамического порога, мгновенной суммой, равной значению релаксационного автоколебания и значению амплитуды внешнего синхронизирующего сигнала, то есть условие внеочередного возбуждения имеет вид: $\bmod \frac{{n\Delta t}}{{{{T}_{c}}}} + {{U}_{c}} \geqslant {{f}_{\partial }}\left( {\bmod \frac{{n\Delta t}}{{{{T}_{c}}}}} \right).$

ИССЛЕДОВАНИЕ РЕЖИМОВ СИНХРОНИЗАЦИИ, ВОЗМОЖНЫХ ПРИ ФОРМИРОВАНИИ ВНИМАНИЯ

Математическая модель синхронизации ансамбля нейронов при формировании внимания представлена ансамблем периферических нейронов, генерирующих импульсы одновременно с ЦН1. Таким образом, исследование режимов синхронизации в терминах модели сводится к исследованию режимов, которые могут иметь место в зависимости от параметров модели. Моделирование позволило идентифицировать следующие пять типов динамики модели: 1) асинхронный режим; 2) полная синхронизация; 3) частичная синхронизация; 4) режим “неправильной” синхронизации; 5) переходный фазодинамический процесс. Нейрон ЦН2 не играет существенной роли в формировании динамики модели, он важен лишь для переключения внимания с одного объекта на другой. В связи с этим в данном разделе этот нейрон из модели исключен. Численные расчеты проводились в основном для модели, содержащей ЦН1 и 200 ПН, которые были разбиты на две группы по 100 ПН в каждой группе. Для удобства иллюстрации результатов ограничимся случаем модели с 10 ПН. Качественно поведение модели с таким уменьшенным числом ПН ничем не отличается от модели, содержащей 200 ПН.

Исследована динамика потенциалов периферических нейронов в случае, когда все связи обнулены. Такая динамика нейронной активности, при которой нейроны работают независимо друг от друга, называется асинхронным режимом. Асинхронный режим, т.е. отсутствие синхронизации, рассчитанный с помощью программы, реализованной на MathLab 7, показан на рис. 2.

Рассмотрена динамика модели, соответствующая режиму полной синхронизации, когда все периферические нейроны имеют одинаковую частоту, равную частоте ЦН1. С содержательной точки зрения это означает настройку процесса внимания на один определенный входной объект. В этом режиме все ПН генерируют импульсы одновременно с ЦН1, при этом соотношение числа импульсов ЦН1 и ПН равно 1 : 1. Генерация импульсов ЦН1 обусловлена достаточно высокими возбуждающими сигналами.

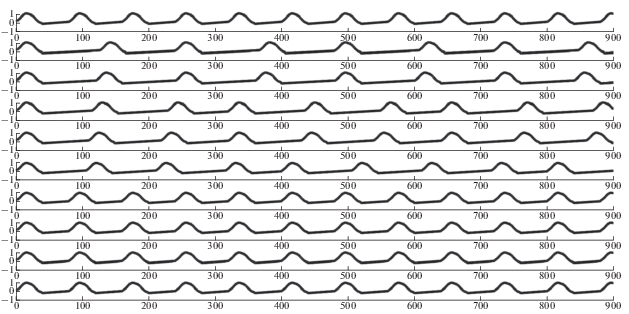
Режим частичной синхронизации занимает как бы промежуточное положение между асинхронным режимом и режимом полной синхронизации. В этом режиме нейроны одной группы срабатывают синфазно с ЦН1, в то время как нейроны другой группы импульсов имеют другие частоты генерации. Режим частичной синхронизации нейронов группы A представлен на рис. 3. Периферические нейроны с номерами от 7 по 10 (последние четыре нейрона) синхронизированы ЦН1, частота генерации которой иллюстрируется первым графиком рисунка. Периферические нейроны с 2 по 6 не синхронизированы.

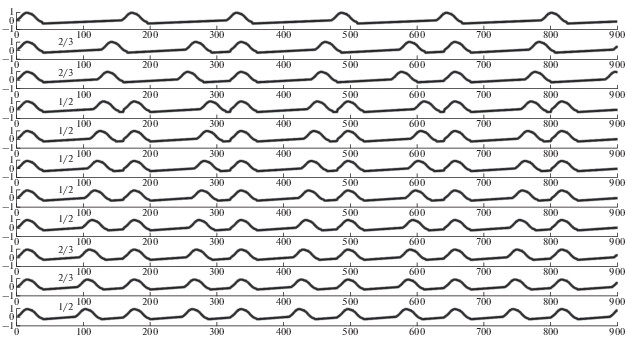
В структуре возможных типов синхронизации существенное место занимают режимы синхронизации, отличные от режима синхронизации типа 1/1, то есть режимы синхронизации типа m/n $\left( {n \ne 1} \right).$ Эти режимы называются режимами “неправильной” синхронизации. Пример таких режимов различного типа показан на рис. 4.

Рассмотрим более детально переходные процессы, происходящие от начала синхронизации до установления стационарной. Экспериментальные исследования показывают, что при вариации параметров переход от одного режима к другому не происходит мгновенно, а проходит через так называемое переходное состояние. Рассмотрим более подробно переходные процессы при синхронизации релаксационных автоколебаний.

ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ СИНХРОНИЗАЦИИ РЕЛАКСАЦИОННЫХ АВТОКОЛЕБАНИЙ – ФАЗОДИНАМИЧЕСКИЕ ПЕРЕХОДНЫЕ ПРОЦЕССЫ

Стационарной синхронизации предшествуют переходные процессы. Установлено, что эти переходные процессы можно разделить на два типа. Это, во-первых, системные переходные процессы и, во-вторых, некоторые специфические переходные процессы, которые будем называть фазодинамическими [2]. Пусть ${{T}_{0}}$ – начальный сдвиг по фазе импульса синхронизации относительно импульса релаксатора. Установлено основное свойство фазодинамических переходных процессов – их максимальная длительность равна длительности ${\varepsilon }$-почти-периода функции, являющейся суммой двух периодических функций – синхронизирующего воздействия и последовательности чувствительных зон.

В начальный момент времени фазы последовательностей импульсов пейсмекера релаксационной автоколебательной системы и синхронизирующего сигнала произвольны; без ограничения общности можно считать их равными ${{T}_{0}}.$ Условие первой синхронизации короткими импульсами можно найти как минимальное решение неравенства Чебышева (4) [7].

Было проведено экспериментальное исследование фазодинамических переходных процессов с помощью компьютерных вычислений. В качестве релаксационной автоколебательной системы использовалась аксиоматическая модель нейрона. Пример одного из таких вычислений показан на рис. 5.

ЗАКЛЮЧЕНИЕ

Исследование синхронизации периферических нейронов от центрального нейрона при формировании внимания позволило идентифицировать следующие пять типов динамики модели: 1) асинхронный режим; 2) полная синхронизация; 3) частичная синхронизация; 4) режим “неправильной” синхронизации; 5) переходный фазодинамический процесс. Переход от полной синхронизации к частичной синхронизации или от частичной синхронизации с одной группой к частичной синхронизации с другой группой проходит в течение определенного времени, что влияет на быстродействие процессов в центральной нервной системе. Ширина полосы синхронизации при реализации процесса внимания возрастает при увеличении числа связей между нейронами и амплитуды синхронизирующего воздействия. С точки зрения нейробиологии этот факт важен потому, что более высокая заметность стимула обычно приводит к более высокой активности нейронов, представляющих этот стимул в коре мозга, и к большей вероятности выбора этого стимула в ФВ [8–18].