Известия РАН. Серия физическая, 2020, T. 84, № 5, стр. 755-760

Математическое и физическое моделирование нестационарных электромагнитных процессов в элементах с самокомпенсацией реактивной мощности

П. А. Бутырин^1, *, Д. В. Михеев¹, Г. Г. Гусев¹, Ф. Н. Шакирзянов¹, М. В. Карпунина¹

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Национальный исследовательский университет “МЭИ”
Москва, Россия

^* E-mail: ButyrinPA@mpei.ru

Поступила в редакцию 02.12.2019
После доработки 23.12.2019
Принята к публикации 27.01.2020

DOI: 10.31857/S0367676520050087

Полный текст (PDF)

Аннотация

Предложена математическая модель для анализа нестационарных электромагнитных процессов в катушке-конденсаторе (катконе) – электромагнитном элементе с самокомпенсацией реактивной мощности. Проведено физическое моделирование переходных процессов в катконе. Обобщены и систематизированы качественные особенности протекания нестационарных электромагнитных процессов на входе и выходе каткона при импульсном воздействии для различных видов нагрузки.

ВВЕДЕНИЕ

Катушка-конденсатор (каткон) является гибридным индуктивно-емкостным элементом, сочетающим в единой структуре свойства индуктивной катушки и конденсатора и реализующим принцип самокомпенсации реактивной мощности [1]. Это определяет его потенциально широкую сферу применения в электронике, радиотехнике, электротехнике и электроэнергетике. Общий принцип построения данного элемента, особенности электрофизических процессов в стационарных режимах и их математическое описание подробно приведены в ряде работ [1–7].

В практическом исполнении каткон представляет собой катушку с двухзаходной намоткой в виде сложенных вместе изолированных друг от друга слоем диэлектрика проводников длиной l, расположенных на магнитном или немагнитном сердечнике [3]. Источник питания подключается к началу первого проводника и к концу второго проводника, конец первого проводника и начало второго проводника могут быть разомкнутыми, замкнутыми или к ним может быть подключена нагрузка с произвольным сопротивлением Z_н [3]. В общем случае каткон представляется линейной или нелинейной электрической цепью с распределенными параметрами (схема замещения цепи элементарной ячейки, содержащей на участке длиной dx первичные параметры, представлена на рис. 1). C учетом ряда допущений и условий, приведенных в [1], относительно входных выводов каткон описывается системой волновых уравнений с учетом (R₀ ≠ 0, G₀ ≠ 0) либо без учета (R₀ = 0, G₀ =0) потерь [1]:

(1)

$\left. \begin{gathered} - \frac{{\partial {{u}_{1}}}}{{\partial х}} = {{L}_{0}}\frac{{\partial ({{i}_{1}} + {{i}_{2}})}}{{\partial t}} + {{R}_{0}}{{i}_{1}} \hfill \\ - \frac{{\partial {{и}_{{\text{2}}}}}}{{\partial х}} = {{L}_{0}}\frac{{\partial ({{i}_{1}} + {{i}_{2}})}}{{\partial t}} + {{R}_{0}}{{i}_{2}} \hfill \\ \frac{{\partial {{i}_{1}}}}{{\partial х}} = - {{C}_{0}}\frac{{\partial ({{u}_{1}} - {{u}_{2}})}}{{\partial t}} - ({{u}_{1}} - {{u}_{2}}){{G}_{0}} \hfill \\ \frac{{\partial {{i}_{2}}}}{{\partial х}} = - {{C}_{0}}\frac{{\partial ({{u}_{2}} - {{u}_{1}})}}{{\partial t}} - ({{u}_{2}} - {{u}_{1}}){{G}_{0}} \hfill \\ \end{gathered} \right\},$

(2)

$\left. \begin{gathered} - \frac{{\partial {{u}_{1}}}}{{\partial х}} = {{L}_{0}}\frac{{\partial ({{i}_{1}} + {{i}_{2}})}}{{\partial t}} \hfill \\ - \frac{{\partial {{и}_{{\text{2}}}}}}{{\partial х}} = {{L}_{0}}\frac{{\partial ({{i}_{1}} + {{i}_{2}})}}{{\partial t}} \hfill \\ \frac{{\partial {{i}_{1}}}}{{\partial х}} = - {{C}_{0}}\frac{{\partial ({{u}_{1}} - {{u}_{2}})}}{{\partial t}} \hfill \\ \frac{{\partial {{i}_{2}}}}{{\partial х}} = - {{C}_{0}}\frac{{\partial ({{u}_{2}} - {{u}_{1}})}}{{\partial t}} \hfill \\ \end{gathered} \right\}.$

Рис. 1.

Схема замещения каткона как электрической цепи с распределенными параметрами: u_вх (В) – напряжение источника питания; i_вх, i₁(x), i₂(x) (А) – входной ток, токи в 1-ом и 2-ом проводниках (i_вх = i₁(x) + i₂(x) = const); u_н (В), i_н (А) – напряжение и ток в нагрузке; L₀₁ = L₀₂ = L₀ (Гн/м) – индуктивность проводников каткона на единицу длины; R₀₁ = R₀₂ = R₀ (Ом/м) – сопротивление проводников каткона на единицу длины; C₀ (Ф/м) – емкость между проводниками на единицу длины; G₀ (См/м) – проводимость на единицу длины, учитывающая потери в изоляции между проводниками; l (м) – длина проводников.

Вторичные параметры каткона имеют следующий вид: волновое сопротивление Z_в = 2R₀/γ, комплексный коэффициент распространения $\underline {\gamma } $ = = $\sqrt {{{R}_{0}}(2j{\omega }{{C}_{0}} + 2{{G}_{0}})} .$

Решение систем (1) и (2) позволяет в аналитическом виде получить распределения токов и напряжений вдоль проводников каткона в стационарных режимах с учетом соответствующих граничных условий (рис. 1):

• режим холостого хода (ХХ) (Z_н → ∞): i₂(0) = = i₁(l) = 0; i₁(0) = i₂(l) = i_вх(t); u₁(0) = u_вх(t); u₂(l) = 0.

• режим короткого замыкания (КЗ) (Z_н = 0) i₂(0) = i₁(l) ≠ 0; i₁(0) = i₂(l) = i_вх(t); u₁(0) = u_вх(t); u₂(0) = u₁(l); u₂(l) = 0.

• режим произвольной нагрузки (Z_н = var): i₁(0) = i₂(l) ≠ 0; i₁(l) = i₂(0) = i_вх(t); u₁(0) = u₂(l) – u_н(t); u₁(l) = 0; u₂(0) = u_вх(l) – u_н(t).

При этом анализ и моделирование нестационарных режимов работы каткона как электрической цепи с распределенными параметрами является труднорешаемой задачей [8]. С другой стороны, применение схем замещения каткона с сосредоточенными параметрами [4–7] не позволяет учесть ряд его особенностей в нестационарных режимах. В этой связи “компромиссным решением” является использование синтезированных относительно входных выводов Н₁ и К₂ (рис. 1) схем замещения каткона с эквивалентными сосредоточенными параметрами (рис. 2а–2в).

Рис. 2.

Синтезированные схемы замещения каткона с эквивалентными сосредоточенными параметрами относительно выводов Н₁ и К₂: (а) – при разомкнутых выводах К₁ и Н₂ (режим холостого хода); (б) – при замкнутых выводах К₁ и Н₂ (режим короткого замыкания).

Таким образом, в настоящей работе ставится задача разработки математической модели для анализа нестационарных (переходных) электромагнитных процессов в гибридном индуктивно-емкостном элементе – катконе. Решение этой задачи позволит изучить физические свойства и особенности поведения каткона при переходных процессах и получить выражения для входных и выходных токов и напряжений в аналитической форме при различных видах нагрузки в нестационарных режимах.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНЫХ ЭЛЕКТРОМАГНИТНЫХ ПРОЦЕССОВ

В рамках поставленной задачи примем допущение о линейности каткона и рассмотрим граничные условия, при которых он представляется электрической цепью второго порядка: режим ХХ (Z_н → ∞), режим КЗ (Z_н = 0), резистивная нагрузка (Z_н = R_н = var) и согласованная нагрузка (Z_н = R_н = 2√L₀/C₀ = 2ρ).

При рассмотрении режимов ХХ и КЗ необходимо использовать расчетные схемы, представленные на рис. 2а, 2б, в остальных случаях – рис. 2в. В зависимости от подключаемого к выходным выводам каткона резистивного сопротивления в общем случае могут наблюдаться колебательный (p_{1, 2} = α ± jω_св, в режиме ХХ и при R_н > 2ρ), предельно-апериодический (p₁ = p₂ = p, при R_н = 2ρ, фактически переходной процесс не будет наблюдаться) и апериодический (p₁ ≠ p₂, в режиме КЗ и при 0 < R_н < 2ρ) характеры переходных процессов, что вытекает из соотношения первичных параметров каткона [8]. Значения корней характеристических уравнений для рассматриваемых случаев приведены в [8].

Однако стоит отметить следующие обстоятельства и ограничения при применении выбранных синтезированных схем замещения для анализа переходных процессов на входе и выходе каткона:

• рассматриваемые схемы замещения могут быть применимы только для расчета входного тока (режим ХХ) и напряжения (режим КЗ и произвольной нагрузки) при воздействии источника на вход каткона;

• при анализе переходных процессов на выходе каткона при воздействии на вход каткона источника тока необходимо использовать синтезированную схему замещения (рис. 2в), при возможности пренебрежения потерями;

• при анализе переходных процессов на выходе каткона при включении и отключении резистивной нагрузки необходимо использовать схему эквивалентного генератора [3].

Так как в рассматриваемых случаях каткон может быть представлен линейной электрической цепью второго порядка, то к расчету такой цепи применимы хорошо известные методы расчета переходных процессов в линейных электрических цепях с сосредоточенными параметрами: классический метод, операторный метод, метод переменных состояния, метод, основанный на применении интеграла Дюамеля, метод фазовой плоскости и др.

При анализе переходных процессов с произвольной комплексной нагрузкой (Z_н = R_н + jωL_н и Z_н = R_н – 1/jωC_н), подключенной к выходным выводам каткона, также можно использовать схему замещения каткона с эквивалентными сосредоточенными параметрами без потерь, приведенную на рис. 2в. После преобразований и замены jω на оператор p для активно-индуктивной и активно-емкостной нагрузок получим:

(3)

${{Z}_{{{\text{вх}}}}}(p) = \frac{{{{p}^{3}}{{L}_{{\text{н}}}}{{C}_{0}}{{L}_{0}}{{l}^{2}} + {{p}^{2}}{{R}_{{\text{н}}}}{{C}_{0}}{{L}_{0}}{{l}^{2}} + p(4{{L}_{0}}l + {{L}_{{\text{н}}}}) + {{R}_{{\text{н}}}}}}{{({{R}_{{\text{н}}}} + p{{L}_{{\text{н}}}})p{{C}_{0}}l + {{p}^{2}}{{C}_{0}}{{L}_{0}}{{l}^{2}} + 1}} = 0.$

(4)

$\begin{gathered} {{Z}_{{{\text{вх}}}}}(p) = \\ = \frac{{{{p}^{3}}{{R}_{{\text{н}}}}{{C}_{{\text{н}}}}{{C}_{0}}{{L}_{0}}{{l}^{2}} - {{p}^{2}}{{C}_{0}}{{L}_{0}}{{l}^{2}} + p(4{{L}_{0}}l{{C}_{{\text{н}}}} + {{R}_{{\text{н}}}}{{C}_{{\text{н}}}}) - 1}}{{p{{C}_{0}}l(p{{R}_{{\text{н}}}}{{C}_{{\text{н}}}} - 1) + p{{C}_{{\text{н}}}}({{p}^{2}}{{C}_{0}}{{L}_{0}}{{l}^{2}} + 1)}} = 0. \\ \end{gathered} $

Из данных уравнений очевидно, что при подключении активно-индуктивной и активно-емкостной нагрузки относительно входных выводов каткон представляется линейной цепью третьего порядка, для которой также применимы вышеназванные методы расчета переходных процессов. В зависимости от соотношения первичных параметров каткона и подключаемой нагрузки в общем виде аналитическое решение для рассматриваемых случаев (рис. 2в, Z_н = R_н + jωL_н и Z_н = R_н – 1/jωC_н) будет иметь следующий вид:

$\begin{gathered} {{u}_{{{\text{вх}}}}} = {{u}_{{{\text{вхуст}}}}} + {{u}_{{{\text{вхпрех}}}}} = {{u}_{{{\text{вхуст}}}}} + {{A}_{0}}{{e}^{{{\alpha }t}}}{\text{sin}}({{{\omega }}_{{{\text{св}}}}}t + {{\Psi }_{{{\text{св}}}}}) + \\ + \,\,B{{{\text{e}}}^{p}}^{{_{3}t}}\,\,\,\,({\text{при}}\,\,\,\,{{p}_{{1,2}}} = {\alpha } \pm j{{{\omega }}_{{{\text{св}}}}};\,\,{{p}_{3}}), \\ \end{gathered} $

$\begin{gathered} {{u}_{{{\text{вх}}}}} = {{u}_{{{\text{вхуст}}}}} + {{u}_{{{\text{вхпрех}}}}} = {{u}_{{{\text{вхуст}}}}} + {{A}_{1}}{{{\text{e}}}^{p}}^{{_{1}t}} + {{A}_{2}}{{{\text{e}}}^{p}}^{{_{2}t}} + \\ + \,\,{{A}_{3}}{{{\text{e}}}^{p}}^{{_{3}t}}\,\,\,\,({\text{при}}\,\,\,\,{{p}_{1}} \ne {{p}_{2}} \ne {{p}_{3}}), \\ \end{gathered} $

где A₀, B, Ψ_св (°), A₁, A₂, A₃ – постоянные интегрирования, ω_св (рад/с) – циклическая частота свободных колебаний, α (с^–1) – коэффициент затухания, p₁, p₂, p₃ (с^–1) – вещественные корни характеристического уравнения.

Рассмотрим задачу включения каткона на источник постоянного (U_вх) и синусоидального (u_вх = U_вхmsin(ωt + φ_u)) напряжения при разомкнутых выходных выводах каткона (рис. 2а, режим ХХ). Результаты расчета переходных процессов классическим методом на входе каткона (определения входного тока i_вх(t)) для рассматриваемых случаев представлены далее.

1. Включение каткона на источник постоянного напряжения U_вх.

Независимые начальные условия: U_C(0_–) = = U_C(0₊) = 0 В; i_L(0_–) = i_L(0₊) = 0 А.

Установившийся режим: i_вхуст = U_вх/(2/3R₀l + + 1/G₀l) А.

Корни характеристического уравнения: p_{1, 2} = = α ± jω_св.

В общем виде: i_вх = i_вхуст + i_вхпрех = U_вх/(2/3R₀l + + 1/G₀l) + A₀e^αtsin(ω_свt + φ_св) А.

Зависимые начальные условия: i_вх(0) = 0 А; di_вх/dt|₀ = U_вх/L₀l А/с.

Решение в аналитической форме:

$\begin{gathered} {{i}_{{{\text{вх}}}}} = \frac{{{{U}_{{{\text{вх}}}}}}}{{\frac{2}{3}{{R}_{0}}l + {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {{{G}_{0}}l}}} \right. \kern-0em} {{{G}_{0}}l}}}} - \,\,\frac{{{{U}_{{{\text{вх}}}}}}}{{\left( {\frac{2}{3}{{R}_{0}}l + {1 \mathord{\left/ {\vphantom {1 {{{G}_{0}}l}}} \right. \kern-0em} {{{G}_{0}}l}}} \right)\sin \left( {{\text{arcctg}}\left[ { - \frac{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}{{R}_{0}}l + {1 \mathord{\left/ {\vphantom {1 {{{G}_{0}}l}}} \right. \kern-0em} {{{G}_{0}}l}} + {\alpha }{{L}_{0}}l}}{{{{{\omega }}_{{{\text{св}}}}}{{L}_{0}}l}}} \right]} \right)}} \times \\ \times \,\,{{{\text{e}}}^{{{\alpha }t}}}{\text{sin}}\left( {{{{\omega }}_{{{\text{св}}}}}t + {\text{arcctg}}\left[ { - \frac{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}{{R}_{0}}l + {1 \mathord{\left/ {\vphantom {1 {{{G}_{0}}l}}} \right. \kern-0em} {{{G}_{0}}l}} + {\alpha }{{L}_{0}}l}}{{{{{\omega }}_{{{\text{св}}}}}{{L}_{0}}l}}} \right]} \right) {\text{А}}{\text{.}} \\ \end{gathered} $

2. Включение на источник синусоидального напряжения u_вх = U_вхmsin(ωt + φ_u).

Обозначения: R_L = 2/3R₀l; L = L₀l; C = C₀l; X_C = = 1/ωC; X_L = ωL.

Независимые начальные условия: U_C(0_–) = = U_C(0₊) = 0 В; i_L(0_–) = i_L(0₊) = 0 А.

Установившийся режим:

$\begin{gathered} {{i}_{{{\text{вхуст}}}}} = {{I}_{{{\text{вхуст}}m}}}\sin \left( {{\omega }t + \left[ {{{{\varphi }}_{u}} - {{{\varphi }}_{Z}}} \right]} \right) = {{{{U}_{{{\text{вх}}m}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{вх}}m}}}} {{{Z}_{{{\text{вхХХ}}}}}}}} \right. \kern-0em} {{{Z}_{{{\text{вхХХ}}}}}}}\sin \left( {{\omega }t + \left[ {{{{\varphi }}_{u}} - {{{\varphi }}_{Z}}} \right]} \right) = \\ = \frac{{{{U}_{{{\text{вх}}m}}}}}{{\sqrt {{{{\left( {{{R}_{L}} + \frac{{{{G}_{0}}l}}{{G_{0}^{2}{{l}^{2}} + {{{\omega }}^{2}}C_{0}^{2}{{l}^{2}}}}} \right)}}^{2}} + {{{\left( {{{X}_{L}} - \frac{{{\omega }{{C}_{0}}l}}{{G_{0}^{2}{{l}^{2}} + {{{\omega }}^{2}}C_{0}^{2}{{l}^{2}}}}} \right)}}^{2}}} }}\,\sin \left( {{\omega }t + \left[ {{{{\varphi }}_{u}} - {\text{arctg}}\left[ {\frac{{{{X}_{L}} - \frac{{{\omega }{{C}_{0}}l}}{{G_{0}^{2}{{l}^{2}} + {{{\omega }}^{2}}C_{0}^{2}{{l}^{2}}}}}}{{{{R}_{L}} + \frac{{{{G}_{0}}l}}{{G_{0}^{2}{{l}^{2}} + {{{\omega }}^{2}}C_{0}^{2}{{l}^{2}}}}}}} \right]} \right]} \right)\,\,{\text{А}}{\text{.}} \\ \end{gathered} $

Корни характеристического уравнения: p_{1, 2} = = α ± jω_св.

Решение в общем виде: i_вх = i_вхуст + i_вхпрех = = I_вхустmsin(ωt + [φ_u – φ_Z]) + A₀e^αtsin(ω_свt + φ_св) А.

Зависимые начальные условия: i_вх(0) = 0 А; di_вх/dt|₀ = U_вхmsin(φ_u)/L А/с.

Решение в аналитической форме:

$\begin{gathered} {{i}_{{{\text{вх}}}}} = {{I}_{{{\text{вхуст}}m}}}\sin \left( {{\omega }t + \left[ {{{{\varphi }}_{u}} - {{{\varphi }}_{Z}}} \right]} \right) - \,\,\frac{{{{U}_{{{\text{вх}}m}}}\sin \left( {{{{\varphi }}_{u}} - {{{\varphi }}_{Z}}} \right)}}{{{{Z}_{{{\text{вхХХ}}}}}\sin \left( {{\text{arcctg}}\left[ { - \frac{{{{Z}_{{{\text{вхХХ}}}}}\sin \left( {{{{\varphi }}_{u}}} \right)}}{{{{{\omega }}_{{{\text{св}}}}}L\sin \left( {{{{\varphi }}_{u}} - {{{\varphi }}_{Z}}} \right)}} + \frac{{{\omega ctg}\left( {{{{\varphi }}_{u}} - {{{\varphi }}_{Z}}} \right) - {\alpha }}}{{{{{\omega }}_{{{\text{св}}}}}}}} \right]} \right)}} \times \\ \times \,\,{{{\text{e}}}^{{{\alpha }t}}}{\text{sin}}\left( {{{{\omega }}_{{{\text{св}}}}}t + {\text{arcctg}}\left[ { - \frac{{{{Z}_{{{\text{вхХХ}}}}}\sin \left( {{{{\varphi }}_{u}}} \right)}}{{{{{\omega }}_{{{\text{св}}}}}L\sin \left( {{{{\varphi }}_{u}} - {{{\varphi }}_{Z}}} \right)}} + } \right.} \right.\left. {\left. {\,\,\frac{{{\omega ctg}\left( {{{{\varphi }}_{u}} - {{{\varphi }}_{Z}}} \right) - {\alpha }}}{{{{{\omega }}_{{{\text{св}}}}}}}} \right]} \right)\,\,{\text{А}}{\text{.}} \\ \end{gathered} $

Аналогичные решения в аналитическом виде могут быть получены для других видов коммутаций при применении известных методов расчета переходных процессов в линейных электрических цепях.

На рис. 3 изображена кривая входного тока каткона (при Z_н → ∞) при подключении к входу каткона источника несинусоидального напряжения, содержащего 1-ую и 3-ю гармоники напряжения с учетом разложения в ряд Фурье [9] (1-ая гармоника: ω₍₁₎ = 578 рад/с, U_вхm(1) = 220√2 В, φ_u(1) = 0°; 3-я гармоника: ω₍₃₎ = ω_св = 1734 рад/с, U_вхm(3) = = 10$\sqrt 2 $ В, φ_u(3) = 30°). Для построения использовались следующие эквивалентные параметры каткона: R₀l = 6.73 Ом, L₀l = 44.6 · 10^–3 Гн, C₀l = = 7.46 · 10^–6 Ф, G₀l = 1 · 10^–5 См [8].

Рис. 3.

Кривая входного тока при подключении к входу каткона источника несинусоидального напряжения, содержащего 1-ю и 3-ю гармоники.

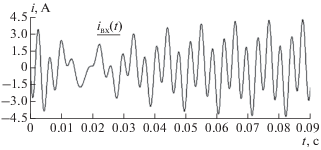
В результате применения метода наложения и вычислений в соответствии с классическим методом было получено мгновенное значение входного тока:

${{i}_{{{\text{вх}}}}}(t) = {{i}_{{{\text{вх}}(1)}}}(t) + {{i}_{{{\text{вх}}(3)}}}(t),$

где

$\begin{gathered} {{i}_{{{\text{вх}}(1)}}}{\text{(}}t{\text{)}} = 1.342\sin \left( {578t + 89.87^\circ } \right)-- \\ - \,\,4.05{{{\text{e}}}^{{--49.59t}}}\sin \left( {1734t + 19.27^\circ } \right)\,\,{\text{А}}; \\ \end{gathered} $

$\begin{gathered} {{i}_{{{\text{вх}}(3)}}}{\text{(}}t{\text{)}} = 3.113\sin \left( {1734t + 30^\circ } \right)-- \\ - \,\,3.113{{{\text{e}}}^{{--49.59t}}}\sin \left( {1734t + 30^\circ } \right)\,\,{\text{А}}. \\ \end{gathered} $

ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕСТАЦИОНАРНЫХ ЭЛЕКТРОМАГНИТНЫХ ПРОЦЕССОВ

Конфигурация и конструктивное исполнение разработанной и исследуемой физической модели каткона с магнитопроводом были подробно описаны в [3]. При экспериментальном исследовании нестационарных электромагнитных процессов к входу физической модели каткона подключался источник напряжения с импульсным сигналом (меандром) с частотой 15.5 Гц и максимальным значением напряжения U_max = 1–2 В, к выходным выводам физической модели каткона подключалась нагрузка (конденсатор, индуктивная катушка, резистор). При варьировании параметров нагрузки были получены осциллограммы входного напряжения и тока. Результаты эксперимента и анализ полученных осциллограмм позволили определить характер и качественные особенности переходных процессов на входе и выходе физической модели каткона, приведенные в табл. 1.

Таблица 1.

Характеристика протекания нестационарных электромагнитных процессов на входе и выходе каткона при импульсном воздействии. Обозначения: A, B, Ψ_св (°) – постоянные интегрирования; ω_св (рад/с) – циклическая частота свободных колебаний; T_св (с) – период свободных колебаний; α (с^–1) и p (с^–1) – коэффициент затухания и вещественный корень характеристического уравнения

Вид нагрузки	Порядок цепи	Характер нестационарного электромагнитного процесса	Особенности нестационарного электромагнитного процесса
Вид нагрузки	Порядок цепи	Характер нестационарного электромагнитного процесса	на входе каткона	на выходе каткона
Режим КЗ (R_н→ 0)	Второй	Апериодический	Кривая тока не изменяется скачком	Кривая тока не изменяется скачком
Резистивная (0 < R_н< 2ρ Ом)	Второй	Апериодический	Кривая тока не изменяется скачком	Кривые напряжения и тока изменяются скачком
Резистивная (R_н= 2ρ Ом)	Второй	Переходной процесс на входе не наблюдается, на выходе – апериодический	Форма кривой тока идентична кривой напряжения	Кривые напряжения и тока изменяются скачком
Резистивная (R_н> 2ρ Ом)	Второй	Колебательный	Кривая тока не изменяется скачком	Кривые напряжения и тока изменяются скачком
Режим ХХ (R_н→ 0)	Второй	Колебательный	Кривая тока не изменяется скачком	Кривая напряжения изменяется скачком
Емкостная (C_н = 3.3–82 мкФ)	Третий	Выражение для преходящей составляющей входного тока в общем виде: i_прех=Ae^αtsin(ω_свt + Ψ_св) + Be^pt, при этом ω_св, α и p по модулю примерно одного порядка	Кривая тока не изменяется скачком. При увеличении значения C_н наблюдается увеличение максимального значения входного тока и периода свободных колебаний T_св	Кривая напряжения не изменяется скачком, кривая тока – изменяется
Индуктивная (L_н = 43.3–130 мГн)	Третий	Выражение для преходящей составляющей входного тока в общем виде: i_прех = Ae^αtsin(ω_свt + Ψ_св) + Be^pt, при этом по модулю ω_св$ \gg $ α и ω_св$ \gg $p	Кривая тока не изменяется скачком. При увеличении значения L_н наблюдается увеличение максимального значения входного тока и периода свободных колебаний T_св	Кривая напряжения изменяется скачком, кривая тока – не изменяется

На рис. 4 представлены экспериментальная (i_exp(t)) и теоретическая (i_theory(t) = 0.04e^–40.2tsin(1714t) А) кривые входного тока при импульсном воздействии источника напряжения на вход физической модели каткона в режиме ХХ. Полученные кривые (рис. 4) позволяют судить об адекватности, точности и возможности применения предложенной математической модели для анализа нестационарных электромагнитных процессов на входе каткона.

Рис. 4.

Теоретическая (i_theory(t)) и экспериментальная (i_exp(t)) кривые входного тока при подключении к входу каткона импульсного источника напряжения.

ЗАКЛЮЧЕНИЕ

1. Предложена математическая модель для расчета нестационарных электромагнитных процессов на входе каткона, основанная на применении классического метода расчета переходных процессов в линейных электрических цепях, ее адекватность подтверждена экспериментально.

2. Установлено, что при разомкнутых и замкнутых выходных выводах, при подключении к ним резистора, катушки и конденсатора каткон можно рассматривать как линейную электрическую цепь второго и третьего порядков.

3. Проведено компьютерное моделирование нестационарных электромагнитных процессов на входе каткона при воздействии несинусоидального источника напряжения.

4. Качественно описаны и систематизированы особенности протекания переходных процессов на входе и выходе каткона при различных видах нагрузки (граничных условиях).

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-08-00730 А.

Список литературы

Демирчян К.С., Гусев Г.Г. // Изв. АН СССР. Сер. Энерг. трансп. 1987. № 2. С. 3.
Konesev S.G., Khazieva R.T., Kirillov R.V. // Proc. Dynamics-2016 (Omsk, 2016). P. 1.
Бутырин П.А., Гусев Г.Г., Михеев Д.В., Шакирзянов Ф.Н. // Изв. РАН. Сер. физ. 2018. Т. 82. № 8. С. 1017; Butyrin P.A., Gusev G.G., Mikheev D.V., Shakirzianov F.N. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. № 8. P. 918.
Konesev S.G., Khazieva R.N., Bochkareva T.A. // Proc. ICIEAM-2018 (Saint-Petersburg, 2018). P. 1.
Konesev S.G., Khazieva R.T., Kirillov R.V. // J. Phys. Conf. Ser. 2019. V. 1210. Art. № 012068.
Reeves R. // Proc. IEE. 1975. V. 122. № 11. P. 1323.
Murgatroyd P.N. // Electrocomp. Sci. Technol. 1976. V. 3. № 2. P. 97.
Бутырин П.А., Гусев Г.Г., Михеев Д.В. и др. // Изв. РАН. Энергетика. 2019. № 1. С. 109.
Gritsutenko S., Korovkin N. // MATEC Web Conf. 2018. V. 245. Art. № 10004.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал