Известия РАН. Серия физическая, 2020, T. 84, № 6, стр. 772-776

Распространение звука в суспензиях: вращательные движения частиц и управление потоками

И. Н. Диденкулов^1, 2, *, Т. С. Корчагина², Н. В. Прончатов-Рубцов², А. А. Сагачева¹

¹ Федеральное государственное бюджетное учреждение науки “Институт прикладной физики Российской академии наук”
Нижний Новгород, Россия

² Федеральное государственное автономное образовательное учреждение высшего образования “Национальный исследовательский Нижегородский государственный университет имени Н.И. Лобачевского”
Нижний Новгород, Россия

^* E-mail: diniap@mail.ru

Поступила в редакцию 16.12.2019
После доработки 20.01.2020
Принята к публикации 26.02.2020

DOI: 10.31857/S0367676520060071

Полный текст (PDF)

Аннотация

Многие реальные жидкости кроме самой жидкой фазы содержат твердые или газовые включения. Эти включения влияют на распространение звука. С другой стороны, звуком можно влиять на распределение концентрации частиц. В работе рассматриваются эти две задачи: затухание звука в суспензии частиц, совершающих вращательные колебания, и формирование неоднородного распределения пузырьков в проточных акустических волноводных системах.

ВВЕДЕНИЕ

Большинство жидкостей, которые встречаются в природе или в технологических процессах, являются суспензиями. Частицы суспензии могут отличаться по плотности и сжимаемости от материнской среды и влияют на скорость и затухание звука [1–3]. Поэтому с помощью акустических волн можно осуществлять диагностику таких сред. Кроме того, подобные среды с микроструктурой как жидкие, так и твердые представляют значительный интерес с точки зрения создания метаматериалов, обеспечивающих оптимальное поглощение звука [4].

Обычно в задачах распространения волн в суспензиях учитываются лишь монопольные и дипольные колебания [5, 6]. Считается, что суспензии частиц нейтральной плавучести, не оказывают влияния на распространение звука. Однако частицы со смещенным центром масс в акустическом поле могут совершать вращательные колебания, которые сопровождаются вязким трением и приводят к потере энергии акустической волны [7]. Центр масс частицы может быть смещен вследствие неравномерного распределения плотности тела или наличия небольшого довеска массы на его поверхности, который в общем случае может быть как положительным, так и отрицательным. Приводится анализ влияния вращательных колебаний частиц на затухание звука в суспензиях, содержащих частицы разной формы.

С другой стороны, акустическое поле само оказывает влияние на частицы в жидкости за счет радиационной силы и может приводить к их перераспределению. Действие радиационной силы хорошо проявляется в экспериментах по сонолюминесценции одиночного пузырька, в которых пузырек удерживается в левитирующем состоянии в акустическом резонаторе [8]. При течении жидкости на пузырьки дополнительно действует сила вязкого трения. Действие радиационной силы и силы вязкого трения в проточном акустическом резонаторе приводит к неравномерному распределению концентрации пузырьков [9, 10]. Приведен анализ изменения концентрации пузырьков в проточных акустических системах.

ЗАТУХАНИЕ ЗВУКА В СРЕДЕ С ЧАСТИЦАМИ СО СМЕЩЕННЫМ ЦЕНТРОМ МАСС

Вращательные движения частиц

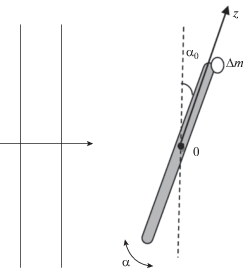
Рассмотрим колебания стержнеподобной частицы со смещенным центром масс. Схема задачи показана на рис. 1. Частица, представляющая собой круглый стержень длиной l и радиусом R, имеет на одном ее краю точечный довесок массы. При этом полагаем, что средняя плотность частицы равна плотности ρ окружающей жидкости, а величина довеска массы ∆m много меньше полной массы частицы m: |∆m| $ \ll $ m, m = πR²lρ. Довесок массы в общем случае может быть как положительным, так и отрицательным, а размеры частицы удовлетворяют соотношению R $ \ll $ l $ \ll $ λ, где λ − длина звуковой волны. Ось цилиндра образует угол α₀ с фронтом плоской звуковой волны.

Рис. 1.

Схема задачи для стержневой частицы.

В акустическом поле частицы жидкости совершают продольные колебания. Если средняя плотность рассматриваемой частицы равна плотности жидкости, она будет совершать такие же колебания. В неинерциальной системе отсчета, связанной с частицей, на нее действует переменная во времени инерциальная сила, которая приводит к возникновению вращающего момента силы M_in. Помимо момента M_in, вызывающего вращательные движения, на частицу действует также момент сил вязкого трения в жидкости M_fr.

Уравнение вращательных колебаний частицы запишется в виде:

(1)

$J\ddot {\alpha } = {{M}_{{in}}} + {{M}_{{fr}}},$

где $\ddot {\alpha }$ – угловое ускорение, J – момент инерции частицы [11].

Момент M_in можно выразить через продольное ускорение а частиц среды в звуковой волне, угол α₀, величину довеска массы ∆m и плечо силы, равное половине длины стержня l/2:

(2)

${{M}_{{in}}} = - (\Delta m)a({l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2})\cos {{\alpha }_{0}}.$

Поскольку ускорение a и скорость u продольных движений частиц среды связана с давлением p, для гармонической плоской волны p = p_aexp(iωt – ikx) имеем:

(3)

${{M}_{{in}}} = - ikp({1 \mathord{\left/ {\vphantom {1 \rho }} \right. \kern-0em} \rho })\left( {\Delta m} \right)\left( {{l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}} \right)\cos {{\alpha }_{0}},$

где k = ω/c − волновое число, ω = 2πf, f – частота, с – скорость звука, ρ − плотность жидкости.

Момент силы вязкого трения M_fr можно найти в предположении, что обтекание каждого малого участка цилиндра длиной dz происходит аналогично обтеканию бесконечного цилиндра потоком жидкости со скоростью υ(z) = $z \cdot \dot {\alpha }$, где $\dot {\alpha }$ = = (dα/dt) – угловая скорость вращательных колебаний. Поскольку скорость обтекания при вращательных движениях стержня линейно зависит от расстояния от оси вращения, основной вклад в силу сопротивления будут давать части стержня удаленные от оси. Основываясь на этом, мы будем пренебрегать различиями в характере обтекания стержня при разных z и используем выражение для силы F_fr, действующей на единицу длины цилиндра при δ $ \ll $ R, где δ(ω) = $\sqrt {{{2\vartheta } \mathord{\left/ {\vphantom {{2\vartheta } \omega }} \right. \kern-0em} \omega }} $ – толщина осциллирующего пограничного слоя, ϑ = η/ρ – кинематическая вязкость, η – динамическая вязкость [3]:

${{F}_{{fr}}} = - 2\pi Rv(z)\sqrt {2\rho \eta \omega } .$

Теперь можно найти момент силы вязкого трения:

(4)

${{M}_{{fr}}} = - 2\int\limits_0^{{l \mathord{\left/ {\vphantom {l 2}} \right. \kern-0em} 2}} {z{{F}_{{fr}}}(z)dz} = - ({\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6})\sqrt {2\omega \vartheta } \rho R{{l}^{3}}\dot {\alpha }.$

Тогда уравнение колебаний стержня (1) можно переписать в виде:

(5)

$\ddot {\alpha } + 2w({\delta \mathord{\left/ {\vphantom {\delta R}} \right. \kern-0em} R})~ = - 6i({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c})({{\Delta m} \mathord{\left/ {\vphantom {{\Delta m} m}} \right. \kern-0em} m})(\cos {{{{\alpha }_{0}}} \mathord{\left/ {\vphantom {{{{\alpha }_{0}}} {\rho l}}} \right. \kern-0em} {\rho l}}){{p}_{a}}{{e}^{i}}^{{\omega t}}.$

Уравнение (5) записано с учетом того, что m = = πR²lρ, а J ≈ ml²/12. Решая уравнение (5), найдем угловые колебания α и угловую скорость $\dot {\alpha }$ стержня:

(6)

$\dot {\alpha } = - \frac{{6\cos {{\alpha }_{0}}({{\Delta m} \mathord{\left/ {\vphantom {{\Delta m} m}} \right. \kern-0em} m})({{{{p}_{a}}} \mathord{\left/ {\vphantom {{{{p}_{a}}} {\rho cl}}} \right. \kern-0em} {\rho cl}})}}{{[1 - 2i({\delta \mathord{\left/ {\vphantom {\delta R}} \right. \kern-0em} R})]}} \cdot {{e}^{{i\omega t}}}.$

Среднюю за период колебаний мощность потерь энергии W (мощность силы трения со знаком минус) можно найти по формуле:

(7)

$W = - \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right){{M}_{{fr}}}(\dot {\alpha })*,$

где звездочка обозначает комплексное сопряжение. Подставляя (4) и (6) в (7) и используя условие (δ/R) $ \ll $ 1, получим

(8)

$W = 3\pi \omega \delta Rl \cdot {{\left( {\frac{{\Delta m}}{m}} \right)}^{2}} \cdot \frac{{p_{a}^{2}}}{{\rho {{c}^{2}}}} \cdot {{\cos }^{2}}{{\alpha }_{0}}.$

Поглощающую способность неоднородностей характеризуют сечением поглощения σ, равным отношению мощности потерь энергии W к интенсивности падающей волны I:

$\sigma = {W \mathord{\left/ {\vphantom {W I}} \right. \kern-0em} I},$

где I = |p_a|²/(2ρc) – интенсивность поля плоской волны,

(9)

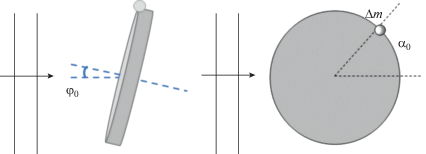
$\sigma = \frac{{6\pi \omega \delta Rl}}{с} \cdot {{\left( {\frac{{\Delta m}}{m}} \right)}^{2}} \cdot {{\cos }^{2}}{{\alpha }_{0}}.$

Можно построить аналогичную модель для дискообразной частицы со смещенным центром масс. Частица представляет собой круглый диск толщиной h, радиусом R_d, который имеет на одном краю точечный довесок массы. Ось диска образует угол φ₀ с волновым вектором акустической волны, а положение довеска массы на диске по отношению к волновому вектору характеризуется углом α₀, как показано на рис. 2. Рассматриваем угловые колебания этой частицы в плоскости диска, предполагая, что в перпендикулярной плоскости ее колебания незначительны.

Рис. 2.

Схема задачи для дискообразной частицы.

Проводя вычисления, аналогичные стрежневой частице, получим выражение для мощности вязких потерь при вращательных колебаниях дискообразной частицы в звуковом поле:

(10)

$W = \frac{{\pi \omega \delta R_{d}^{2}}}{2}{{\left( {\frac{{\Delta m}}{m}} \right)}^{2}} \cdot \frac{{p_{a}^{2}}}{{\rho {{c}^{2}}}} \cdot {\text{si}}{{{\text{n}}}^{{\text{2}}}}{{\alpha }_{0}} \cdot {\text{si}}{{{\text{n}}}^{{\text{2}}}}{{\varphi }_{0}}.$

Сечение поглощения для дискообразной частицы имеет вид:

(11)

$\sigma = \frac{{\pi \omega \delta R_{d}^{2}}}{c}{{\left( {\frac{{\Delta m}}{m}} \right)}^{2}} \cdot {\text{si}}{{{\text{n}}}^{{\text{2}}}}{{\alpha }_{0}} \cdot {\text{si}}{{{\text{n}}}^{{\text{2}}}}{{\varphi }_{0}}.$

Затухание звука в суспензии частиц

Рассмотрим дополнительное затухание звука в среде, содержащей множество частиц, совершающих вращательные колебания. Если концентрация частиц в среде n, то коэффициент затухания звука εимеет вид:

(12)

$\varepsilon = n\sigma .$

Подставляя в (12) соответствующие выражения (9) и (11) и проводя усреднение по углам, полагая, что ориентации частиц в суспензии равномерно распределены по всем направлениям, получим формулы для коэффициента затухания звука ε_r в суспензии стержнеподобных частиц:

(13)

${{\varepsilon }_{r}} = \frac{{3\pi \omega \delta Rl({{\Delta m} \mathord{\left/ {\vphantom {{\Delta m} m}} \right. \kern-0em} m}){}^{2}}}{c} \cdot n.$

Аналогичная формула для суспензии дискообразных частиц имеет вид:

(14)

${{\varepsilon }_{d}} = \frac{{\pi \omega \delta R{}_{d}^{2}}}{{4c}}{{\left( {\frac{{\Delta m}}{m}} \right)}^{2}}{\kern 1pt} \cdot n,$

где δ(ω) = $\sqrt {{{2\vartheta } \mathord{\left/ {\vphantom {{2\vartheta } \omega }} \right. \kern-0em} \omega }} $ – толщина осциллирующего пограничного слоя.

Используя формулы (13) и (14), сделаем оценку возможной величины эффекта. Прежде всего, отметим, что коэффициент затухания одинаково зависит от частоты для обеих частиц как ω^1/2. Кроме того, нетрудно видеть, что отношение коэффициентов затухания ε_r/ε_d = 12Rl/$R_{d}^{2}$ и при l ≈ R_d, R/l ≈ ≈ 0.1ε_r/ε_d ≈ 1.

Для суспензии на основе воды (ϑ = 10^–6 м² ⋅ с^–1, с =1480 м ⋅ с^–1) и при следующих параметрах l = = 0.1 мм, R = 0.01 мм, ∆m/m = 0.2; n = 10¹² м^–3 коэффициент затухания звука, обусловленного данным механизмом, составляет 4 дБ ⋅ м^–1 на частоте f =1 МГц и 7 дБ ⋅ м^–1 на частоте f = 3 МГц. Эти оценки показывают, что данный механизм затухания может быть существенным даже для водных суспензий, и особенно для более вязких жидкостей.

ДЕЙСТВИЕ АКУСТИЧЕСКОГО ПОЛЯ НА РАСПРЕДЕЛЕНИЕ ПУЗЫРЬКОВ В ПРОТОЧНЫХ СИСТЕМАХ

Рассмотрим движение пузырька в вертикально ориентированном акустическом резонаторе с жесткими стенками, в котором имеется однородное течение жидкости со скоростью V, ориентированной вдоль оси х вертикально вниз.

Предполагаем, что в резонаторе распространяется поршневая мода. При совпадении частоты акустического поля с одной из собственных частот такого резонатора поле представляет собой сумму двух встречных плоских акустических волн:

(15)

$p = \left( {{{p}_{a}}{{e}^{{ikx}}} + {{p}_{a}}{{e}^{{ - ikx}}}} \right){{e}^{{i{\omega }t}}} = 2{{p}_{a}}{{e}^{{i{\omega }t}}}\cos kx,$

где k = ω ⋅ c^–1 – волновое число, p_a – амплитуда звуковой волны, с – скорость звука в жидкости.

На движущийся пузырек действуют сила вязкого трения (сила Стокса) F_St, сила Архимеда F_a и радиационная сила F_r. Сила Стокса имеет вид [3]:

(16)

${{F}_{{St}}} = 6\pi {{R}_{0}}\eta (V - {{V}_{b}}),$

где V_b – скорость пузырька, V – скорость потока жидкости, η – коэффициент динамической вязкости, R₀ – радиус пузырька.

(17)

${{F}_{a}} = - {\rho }g\frac{4}{3}{\pi }R_{0}^{3},$

где ρ – плотность жидкости, g – ускорение свободного падения.

Усредненное за период значение радиационной силы [9, 10]:

(18)

${{F}_{r}} = \frac{{{\pi }{{R}_{0}}^{3}}}{{3{\gamma }{{P}_{0}}\left( {1 - \frac{{{{{\omega }}^{2}}}}{{{{{\omega }}_{0}}^{2}}} - i\delta } \right)}}\nabla {{\left| p \right|}^{2}},$

где δ – декремент затухания, ω₀ = (1/R₀)(3γP₀/ρ)^1/2 – собственная частота пузырька, γ – параметр адиабаты для газа в пузырьке, P₀ – внешнее статическое давление.

Движение пузырьков в жидкости является квазиравномерным. В этом случае сумма сил равна нулю. Подставив выражения для сил, после преобразований получим следующее уравнение для координаты пузырька x_b:

(19)

$\frac{{~d{{x}_{b}}}}{{dt}} = - V + \frac{A}{a}\sin 2k{{x}_{b}} + \frac{b}{A},$

где $~A = - \frac{{4{{p}_{a}}^{2}k{\pi }R_{0}^{3}}}{{3{\gamma }{{P}_{0}}\left( {1 - \frac{{{{{\omega }}^{2}}}}{{{\omega }_{0}^{2}}}} \right)}},$ a = 6πR₀η, $b = {\rho }g\frac{4}{3}{\pi }R_{0}^{3}.$

В общем случае решение уравнения (4) дает следующий результат:

(20)

$\begin{gathered} {{x}_{b}} = \frac{1}{k}{\text{arctg}}\left[ {\sqrt {1 - {{h}^{2}}} {\text{tg}}\left( {\frac{{kt\left( {b - aV} \right)}}{a}\sqrt {1 - {{h}^{2}}} } \right.} \right. + \\ \left. {\left. { + \,\,{\text{arctg}}\left( {\frac{{{\text{tg}}\left( {k{{x}_{0}}} \right) + h}}{{\sqrt {1 - {{h}^{2}}} }}} \right)} \right) - h} \right], \\ \end{gathered} $

где $~~h = \frac{A}{{b\left( {1 - qV} \right)}},$ $q = \frac{a}{b}.$

Выражение (20) описывает неравномерное движение пузырька в проточном резонаторе. Такая ситуация имеет место, если сумма сил Стокса и Архимеда превышает максимальное значение радиационной силы. В обратном случае возможна левитация пузырьков в соответствующих зонах стоячей волны. Прохождение пузырьком узлов и пучностей стоячей волны приводит к изменению радиационной силы, под действием которой меняется скорость квазиравномерного движения пузырька. Если в такой резонатор последовательно запускать пузырьки, то расстояние между ними в процессе движения через резонатор будет изменяться, и, следовательно, концентрация пузырьков также будет испытывать периодические изменения.

В акустических волноводах, в которых возбуждены определенные поперечные моды, радиационная сила (18) будет вызывать перемещение пузырьков в поперечном направлении: маленькие пузырьки, размер которых меньше резонансного для частоты волны, будут смещаться в область максимума поля, а большие – выталкиваться из нее. При этом в продольном направлении для бегущей волны радиационная сила (18) равна нулю и пузырьки будут двигаться со скоростью течения жидкости.

Создавая акустическое поле необходимой конфигурации, можно управлять распределением концентрации пузырьков разных размеров в проточных волноводах и резонаторах.

ЗАКЛЮЧЕНИЕ

В работе рассмотрены два эффекта взаимодействия акустического поля с частицами суспензии. В первом случае предложена модель затухания звука в результате вращательно-колебательных движений частиц нейтральной плавучести, на основе которой вычислены потери энергии за счет вязкого трения. Выполнены оценки дополнительного затухания, которое может быть существенным, особенно на высоких частотах. Рассмотренный механизм угловых колебаний частиц, необходимо учитывать при анализе распространения звука в различных суспензиях и при разработке методов их диагностики, а также при создании метаматериалов с заданными поглощающими свойствами. Кроме того, вблизи частиц, совершающих вращательные колебания, возникает соответствующее движение жидкости в пограничном слое, которое может оказывать воздействие на другие частицы или стенки сосуда, способствуя очистке поверхностей.

Во втором случае рассмотрено воздействие акустического поля на пространственное распределение частиц суспензии – пузырьков в проточных акустических волноводах и резонаторах. Полученное аналитическое решение для зависимости координаты пузырьков от времени позволяет анализировать распределение их концентрации. Это дает возможность решать задачи по формированию акустических полей необходимой конфигурации для управления потоками пузырьков и других малых частиц.

Работа выполнена при поддержке РФФИ (проект № 19-02-00317) и в рамках госзадания 0035-2019-0009 ИПФ РАН. Вторая часть работы выполнена при поддержке РНФ (Н.В.П-Р; проект № 19-12-00256).

Список литературы

Стрэтт Дж.В. Теория звука. Т. 2. М.: Гостехиздат, 1955. 745 с.
Исакович М.А. Теоретические основы акустики. М.: Наука, 1973. 496 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. М.: Наука, 1986. 736 с.
Бобровницкий Ю.И., Томилина Т.М. // Акуст. журн. 2018. Т. 64. № 5. С. 517; Bobrovnitskii Y.I., Tomilina T.M. // Acoust. Phys. 2018. V. 64. № 5. P. 519.
Лебедев-Степанов П.В., Рыбак С.А. // Акуст. журн. 2009. Т. 55. № 3. С. 326; Lebedev-Stepanov P.V., Rybak S.A. // Acoust. Phys. 2009. V. 55. № 3. P. 329.
Лебедев-Степанов П.В., Руденко О.В. // Акуст. журн. 2009. Т. 55. № 6. С. 706; Lebedev-Stepanov P.V., Rudenko O.V. // Acoust. Phys. 2009. V. 55. № 6. P. 729.
Диденкулов И.Н., Езерский А.Б., Селивановский Д.А. // Акуст. журн. 2003. Т. 49. № 3. С. 425; Didenkulov I.N., Ezerskiǐ A.B., Selivanovskiǐ D.A. // Acoust. Phys. 2003. V. 49. № 3. P. 361.
Brenner V.P., Hilgenfeld S., Lohse D. // Rev. Mod. Phys. 2002. V. 74. P. 425.
Токмаков П.Е., Гурбатов С.Н., Диденкулов И.Н., Прончатов-Рубцов Н.В. // Вест. ННГУ. 2006. Сер. Радиофиз. № 1(4). С. 31.
Тихонов В.А., Диденкулов И.Н., Прончатов-Рубцов Н.В. // Акуст. журн. 2013. Т. 59. С. 445; Tikhonov V.A., Pronchatov-Rubtsov N.V., Didenkulov I.N. // Acoust. Phys. 2013. V. 59. № 4. P. 393.
Тарг С.М. Краткий курс теоретической механики. М.: Высшая школа, 1995. 415 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал