Известия РАН. Серия физическая, 2020, T. 84, № 7, стр. 951-956
Расчет структурных характеристик аморфных тел методом молекулярных функций распределения
Ю. В. Аграфонов 1, *, И. С. Петрушин 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Иркутский государственный университет”
Иркутск, Россия
* E-mail: agrafonov@physdep.isu.ru
Поступила в редакцию 14.02.2020
После доработки 16.03.2020
Принята к публикации 27.03.2020
Аннотация
Проведен обзор теоретических методов исследования молекулярной структуры жидкостей и аморфных тел, включая переходы из одного состояния в другое. Обзор литературы показал, что на данный момент нет аналитического решения интегральных уравнений для частичных функций распределения для описания поверхностной аморфизации расплава. Предложено уравнение, допускающее аналитическое решение для системы твердых сфер вблизи твердой поверхности.
ВВЕДЕНИЕ
При исследовании аморфизации расплава необходимо знать его структуру на молекулярном уровне. Однако анализ локальной молекулярной структуры жидкостей является сложной задачей, поскольку жидкости локально упорядочены, но дальний порядок, характерный для кристаллов, в них отсутствует. Тем не менее, было разработано много теоретических методов, позволяющих рассчитывать локальную микроструктуру жидкостей расплавов с последующей кристаллизацией или аморфизацией. Среди них наиболее широко используются: метод численного эксперимента и метод интегральных уравнений для частичных функций распределения, релаксационные теории стеклования и вязкого течения стеклообразующих расплавов многокомпонентного состава, теория “случайного перехода первого рода” из переохлажденной жидкости в идеальное стекло (обобщение метода интегральных уравнений). Как правило, приходится прибегать к каким-либо феноменологическим представлениям о структуре исследуемой жидкости или расплава, либо численно решать сложные интегральные уравнения для частичных функций распределения. Аналитические решения возможны лишь для некоторых частных случаев. Отметим, что на данный момент нет аналитического решения интегральных уравнений для практически важной задачи о поверхностной аморфизации расплава. Поэтому формулировка интегрального уравнения, допускающего аналитическое решение, остается актуальной задачей.
ОБЗОР ИССЛЕДОВАНИЙ В ОБЛАСТИ
Мы рассматриваем современное состояние физики жидкостей и аморфных тел. Проведен обзор теоретических методов исследования молекулярной структуры жидкостей и аморфных тел, включая переходы из одного состояния в другое.
Растворы, расплавы, жидкости
При исследовании аморфизации расплава необходимо знать его структуру на молекулярном уровне. Однако анализ локальной молекулярной структуры жидкостей является сложной задачей, поскольку жидкости локально упорядочены, но дальний порядок, характерный для кристаллов, в них отсутствует. Как следствие, дифракционная картина жидкостей содержит ограниченное количество информации о структуре. Тем не менее, было разработано много методов, среди которых наиболее широко используются рассеяние нейтронов и дифракцию рентгеновских лучей. Измеряя сферически усредненную рассеянную интенсивность I(θ), рассчитывают структурный фактор S(q). Последующее Фурье преобразование S(q) определяет парную корреляционную функцию g(r), т.е. распределение межатомных расстояний. Кроме того, компьютерное моделирование структуры жидкостей внесло значительный вклад в наше понимание жидких фаз (например, моделирование по методу Монте-Карло, молекулярная динамика ab initio, обратный анализ по методу Монте-Карло). Например, в [1] описаны различные подходы к исследованию жидкостей для различных систем и масштабов от простейших металлических структур до более сложных полупроводниковых сплавных структур, которые представляют наибольший интерес в силу их практической значимости для микроэлектроники. В работе [2] рассмотрены основные структурные величины, используемые для характеристики аморфных полупроводников. Проведено сравнение этих величин соответственно для кристаллов и неупорядоченной аморфной системы. Определение структуры аморфных полупроводников до сих пор остается нерешенной задачей, несмотря на десятилетия целенаправленных усилий и отчасти объясняется неполнотой наших знаний о природе аморфного состояния вещества.
Аморфизация жидкостей и расплавов
В настоящее время существует два представления о структуре аморфного состояния. Согласно традиционному взгляду, основанному на методе молекулярных функций распределения [3], “переход в стеклообразное состояние происходит при соответствующем повышении плотности или понижении температуры системы, уже находящейся в метастабильном плотном состоянии. Важно подчеркнуть, что переход в аморфное состояние не является фазовым переходом какого-либо рода. Это явление в значительной мере кинетическое, возникающее на пересечении скорости проведения эксперимента и времени структурной перестройки”. Использование различных замыканий для парных корреляционных функций позволило построить фазовую диаграмму (рис. 1) Леннард-Джонсовской жидкости, на которой выделены две ветви стеклования – стекло G1 и стекло G2.
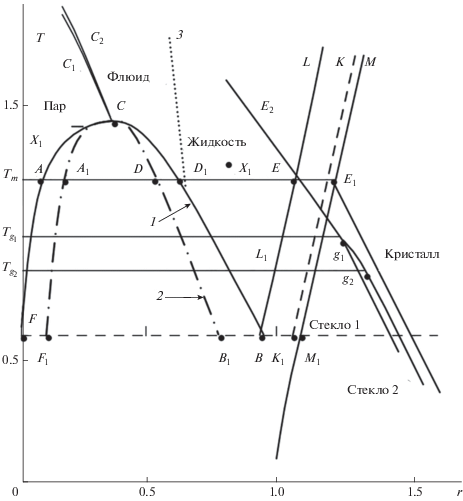
Рис. 1.
Полная фазовая диаграмма системы Леннард-Джонса. Линия FCB является линией фазовых равновесий пар–жидкость (бинодаль, 1); LL1 –линия кристаллизации; MM1 – линия плавления; F1СB1 – граница абсолютной устойчивости однородных фаз (спинодаль, 2) газо-жидкостной области; KK1 – спинодаль плавления. Спинодали кристаллизации не существует, метастабильные состояния переохлаждения и пережатия жидкостей продолжаются и в область кристаллических значений температуры и плотности. C – критическая точка ρ = nσ3 ≈ 0.31, T* = kT/ε ≈ 1.31; B – тройная точка ρ ≈ 0.85, T* ≈ 0.67; Tm – температура равновесного фазового перехода кристаллизация–плавление; ${{T}_{{{{g}_{1}}}}},$ ${{T}_{{{{g}_{2}}}}}$ – температуры аморфных переходов; СС1 и СС2 – линии нулевых значений первого минимума парной корреляционной функции $h\left( {\vec {r}} \right)$ и линия максимальных значений приведенной изотермической сжимаемости χ. Эти линии, а также линия Фишера–Уидома (3) делят всю газо-жидкостную область фазовой диаграммы на три домена: “пар”, “флюид” и “жидкость”. Линия EE2 объединяет точки стабильных жидких состояний; ${{E}_{{{{g}_{1}}}}}$ и ${{E}_{{{{g}_{2}}}}}$ – линии метастабильных состояний в области критических значений параметров. Стекло 1 и Стекло 2 обозначают аморфные состояния.
С другой стороны, после публикации Мезара и Паризи [4], начала интенсивно развиваться теория реплик “случайного перехода первого порядка” (RFOT) из переохлажденной жидкости в “идеальное” стекло. В работе [5] рассчитаны параметры порядка и свободная энергия жидкой и стеклообразной фазы системы “мягких сфер” с использованием гиперцепной аппроксимации (HNC) для парных корреляционных функций. Расчеты подтверждают существование двух ветвей – стекло G1 и стекло G2. Проанализирована зависимость свободной энергии от параметров порядка и устойчивость к спинодальному распаду. Критическая температура оказывается зависимой от параметра порядка m, что может быть следствием погрешности, присущей замыканию HNC. Проанализировано поведение свободной энергии идеальной G2 фазы ниже критической температуры в зависимости от параметра m.
Отметим, также работу [6]. Авторы исследовали структурное и термодинамическое поведение глубоко переохлажденной жидкости Леннард-Джонса при случайном переходе первого порядка (RFOT) к идеальному стеклу с использованием системы двух слабо связанных реплик и интегрального гиперцепного уравнения для парной корреляционной функции. На фазовой диаграмме плотность–температура выявлено существование двух ветвей “стекло G1” и “стекло G2” ниже пороговой температуры, зависящей от плотности. Ветвь более низкой свободной энергии демонстрирует быстрый рост параметра порядка структурного перекрытия при охлаждении и может быть отождествлена с идеальной фазой стекла, как для спиновых, так и для структурных стекол. Полученный в работе характерный резкий разрыв параметра порядка, интерпретируется как слабый переход первого рода с термодинамической точки зрения. Критическая температура перехода быстро возрастает с плотностью и приблизительно подчиняется соотношению, справедливому для системы частиц, взаимодействующих через чисто отталкивающий потенциал r–12.
Доказательство равновесного стеклования жидкость – идеальное стекло приведено в [7]. Авторы решают интегральные уравнения в гиперцепном приближении (HNC) и уравнения Роджерса–Янга (RY) для парной корреляционной функции двухкомпонентной жидкости с межмолекулярными потенциалами мягкой сферы, с целью обнаружить признаки равновесного перехода к “идеальному стеклу”. Оба интегральных уравнения предсказывают, помимо ветви переохлажденной жидкости, появление нового неупорядоченного состояния, характеризующегося различными парными корреляциями в заданном диапазоне температур.
Анализ применимости использованного в [5‒7] гиперцепного приближения приведен в [8]. В данной работе парная корреляционная функция, свободная энергия и конфигурационный параметр порядка переохлажденной жидкости “мягких сфер” определяются путем решения гиперцепного уравнения (HNC) и самосогласованных интегральных уравнений Роджерса–Янга (RY) в широком диапазоне термодинамических условий на фазовой диаграмме ρ–T (плотность–температура) и параметров порядка. С другой стороны, опубликована работа [9], в которой численным моделированием показано, что двухкомпонентная система бинарной смеси твердых сфер претерпевает фазовый переход в состояние равновесия с плотностью немного меньше плотности стеклования для однокомпонентной системы. Этот результат согласуется с теориями [5–8], предсказывающими, что такой переход является предвестником стандартного идеального стеклования.
Выделим две работы [10, 11], посвященные традиционному анализу термодинамической согласованности приближенных интегральных уравнений для парных корреляционных функций. В работе [10] отмечается, что теория интегральных уравнений Орнштейна–Цернике является мощным подходом к простым жидкостям из-за ее низкой вычислительной стоимости и того факта, что в сочетании с соответствующим уравнением замыкания теория является термодинамически полной. Однако, предложенные на сегодняшний день приблизительные замыкания демонстрируют несоответствия давления или свободной энергии, которые приводят к неточным или неоднозначным результатам, ограничивая полезность подхода Орнштейна–Цернике. Для решения этой проблемы авторы объединяют методы обеспечения согласованности давления и свободной энергии, чтобы создать новое приближенное замыкание и проверить его для однокомпонентной жидкости Леннард-Джонса. Замыкание представляет собой простой степенной ряд в прямых и парных корреляционных функциях, для которых получены аналитические формулы для избыточной свободной энергии Гельмгольца и химического потенциала. Рассчитаны давление, свободная энергия Гельмгольца и химический потенциал для жидкости Леннард-Джонса. Эти результаты сравниваются с результатами из гиперцепного уравнения и модифицированного замыкания Верле по сравнению с данными Монте-Карло и уравнений состояния для приведенных плотностей ρ* < 1 и температур T * = 1.5, 2.74 и 5. Предложенное авторами замыкание показывает согласованность между всеми термодинамическими параметрами, за исключением одного выражения в соотношении Гиббса–Дюгема, тогда как гиперцепное уравнение и модифицированное замыкание Верле демонстрируют согласованность только между несколькими параметрами. Точность данного замыкания сопоставима с модифицированным замыканием Верле и дает значительно лучшие результаты по сравнению с гиперцепным уравнением.
В работе [11] анализируется причина, по которой жидкостное приближение в построении функционала плотности не получила такого же развития, как квантовая теория функционала электронной плотности. Отмечается, что в основе теории Орнштейна–Цернике лежит минимальное гильбертово пространство по сравнению с полным пространственным, вращательным и внутренним конформационным пространством квантового функционала электронной плотности. Для устранения отмеченного недостатка предложено два новых базисных разложения: многополярное распределение (наиболее полезное для гибких молекул) и вращательное распределение (наиболее полезное для твердых тел).
Молекулярная система вблизи твердой поверхности
Для вычисления термодинамических характеристик граничных слоев жидкостей недостаточно знать только парную корреляционную функцию. Кроме нее необходимо знать еще и одночастичную функцию распределения, через которую вычисляются поверхностная адсорбция и поверхностное натяжение. Подробный анализ методов вычисления одночастичной функции распределения приведен в работах [12–14].
Однако можно использовать и другие представления. В частности, в [15] рассматривается жидкость твердых сфер в контакте с плоской твердой стенкой. Комбинируя вириальные ряды и результаты численного моделирования, авторы предложили новый критерий точности для расчета поверхностных термодинамических свойств, таких как поверхностная адсорбция Γ и поверхностная свободная энергия (или поверхностное натяжение) γ. Обсуждена проблема выбора системы отсчета для граничной поверхности. Предложено использовать альтернативные функции для Γ и γ, которые не зависят от принятой системы отсчета. Наконец, приведены аналитические выражения для зависимости термодинамических свойств поверхностной системы от плотности жидкости.
Отдельно отметим работу [16], в которой исследовалась поверхностная аморфизация Изинг-нанопровода. С использованием теории эффективного поля получены фазовые диаграммы и тепловые вариации полной намагниченности. Обнаружены некоторые новые явления. Кроме того, сравниваются и обсуждаются фазовые диаграммы в двух поперечных нанопроводах Изинга с поверхностной аморфизацией.
ПОСТАНОВКА ЗАДАЧИ
Микроскопический подход в физике жидкостей основан на уравнениях БГК (Борна–Грина–Кирквуда) для l-частичных функций распределения ${{G}_{{1,...,l}}} = \left( {{{{\vec {r}}}_{1}},...,{{{\vec {r}}}_{l}}} \right).$ Рассматривается ансамбль тождественных частиц, взаимодействующих друг с другом посредством потенциала Φij(rij), где ${{r}_{{ij}}} = \left| {{{{\vec {r}}}_{i}} - {{{\vec {r}}}_{j}}} \right|$ – расстояние между центрами частиц i, j. Уравнения БГК преобразуются к уравнениям для одно- и двух-частичных функций распределения, которые можно записать в форме Орнштейна–Цернике [17]
(1)
$\begin{gathered} {{\omega }_{1}} = n\int {{{G}_{2}}C_{{12}}^{{(1)}}d\left( 2 \right) + \mu ,} \\ {{h}_{{12}}} = C_{{12}}^{{(2)}} + n\int {{{G}_{3}}C_{{13}}^{{(2)}}{{h}_{{23}}}d\left( 3 \right).} \\ \end{gathered} $Интегрирование ведется по координатам i‑й частицы d(i) ≡ dri; n – плотность; Gi = = exp(‒Фi/kT + ωi) – одночастичная функция распределения, описывающая положение частицы в лабораторной системе координат; Фi –потенциальная энергия частицы во внешнем поле; ωi – одночастичный термический потенциал; μ – химический потенциал, определяемый из условия перехода к пространственно-однородной системе; hij = = [exp(–Фij/kT + + ωij) – 1] – парная корреляционная функция, связанная с двухчастичной функцией распределения соотношением Gij = GiGj, (1 + hij); ωij – двухчастичный термический потенциал учитывающий опосредованное взаимодействие двух частиц через их окружение; $C_{{ij}}^{{(k)}}$ – прямые корреляционные функции:
(2)
$\begin{gathered} C_{{ij}}^{{(1)}} = {{h}_{{ij}}} - {{\omega }_{{ij}}} - \frac{1}{2}{{h}_{{ij}}}\left( {{{\omega }_{{ij}}} + M_{{ij}}^{{(1)}}} \right), \\ C_{{ij}}^{{(2)}} = {{h}_{{ij}}} - {{\omega }_{{ij}}} + M_{{ij}}^{{(2)}}. \\ \end{gathered} $Здесь $M_{{ij}}^{{(1)}},$ $M_{{ij}}^{{(2)}}$ – бесконечные функциональные ряды от искомых функций распределения. При решении конкретных задач эти ряды функционалы $M_{{ij}}^{{(1)}},$ $M_{{ij}}^{{(2)}}$ аппроксимируют простыми аналитическими выражениями, что приводит к нелинейным интегральным уравнениям. Наиболее известными из них являются гиперцепное, Перкуса–Йевика, Мартынова–Саркисова.
Особенно большое значение имеет случай пространственно-однородных изотропных сред (объeмные жидкости в отсутствии внешних полей и вдали от ограничивающих поверхностей), в которых: ${{G}_{1}}\left( {\vec {r}} \right) \equiv 1,$ ${{\omega }_{1}}\left( {\vec {r}} \right) = 0,$ $C_{{12}}^{{(1)}}\left( {{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}}} \right)$ = = $C_{{12}}^{{(1)}}\left( {{{r}_{{12}}}} \right).$ В результате первое уравнение системы (1), (2) вырождается в определение избыточного химического потенциала μ = ln a =const. Второе уравнение определяет прямую корреляционную функцию $C_{{12}}^{{(2)}}\left( {{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}}} \right)$ = $C_{{12}}^{{(2)}}\left( {{{r}_{{12}}}} \right),$ для вычисления которой существуют хорошо разработанные методы. Отметим, что в уравнении Перкуса–Йевика прямая корреляционная функция есть $C_{{12}}^{{(2)}}\left( {{{r}_{{12}}}} \right)$ = ${{h}_{{12}}} - \left( {\exp \left( {{{\omega }_{{12}}}} \right) - 1} \right).$ В результате для системы твердых сфер экспоненциальная нелинейность сменяется квадратичной нелинейностью, т.е. становится значительно слабее. Тем самым оказывается возможным получить аналитическое решение [18].
Для пространственно-неоднородных систем (молекулярная система вблизи твердой поверхности) функции ${{G}_{1}} = \left( {{{{\vec {r}}}_{1}}} \right),$ ${{G}_{{12}}} = \left( {{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}}} \right)$ описывают микроструктуру вещества и позволяют рассчитать все термодинамические параметры. Непосредственное решение уравнений (1), (2) для этих функций многих переменных, требует больших численных расчетов. Упростить задачу можно, если вместо прямой корреляционной функции $C_{{12}}^{{(1)}}\left( {{{{\vec {r}}}_{1}},{{{\vec {r}}}_{2}}} \right)$ использовать еe граничное значение $C_{{12}}^{{(1)}}\left( {{{r}_{{12}}}} \right).$ Тогда, в зависимости от замыкания, применяемого для вычисления, $M_{{ij}}^{{\left( {\text{1}} \right)}},$ получается то или иное синглетное уравнение, описывающее профиль локальной плотности $n\left( {{{{\vec {r}}}_{1}}} \right)$ = $n{{G}_{1}}\left( {{{{\vec {r}}}_{1}}} \right)$ вблизи твердой поверхности. Все они являются нелинейными интегральными уравнениями и решаются численно. Обзор их решений приведен в упоминавшейся выше работе [17].
Для молекулярной системы, граничащей с твердой поверхностью, численное решение системы уравнений (1), (2) требует огромных вычислительных ресурсов. Поэтому стараются решать только уравнение для одночастичной функции распределения, аппроксимировав парную функцию распределения ее значением вдали от поверхности, так называемое синглетное приближение. В результате получается нелинейное интегральное уравнение для одночастичной функции распределения, зависящей только от одной переменной – расстояния от частицы до поверхности. Данное уравнение также решается численно, однако уже не требует больших вычислительных ресурсов. Обзор синглетных приближений приведен в уже ставшей классической работе [12]. Отметим, что аналитическое решение для одночастичной функции распределения возможно лишь для частных случаев, например для одномерной и двумерной задачи [19].
Мы предлагаем модификацию синглетного приближения, допускающего аналитическое решение для системы твердых сфер вблизи твердой поверхности.
УРАВНЕНИЕ ДЛЯ ОДНОЧАСТИЧНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ В ПРИБЛИЖЕНИИ ПЕРКУСА–ЙЕВИКА. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
Модифицируем теперь синглетное уравнение в приближении Перкуса–Йевика для молекулярной системы твердых сфер вблизи твердой поверхности. Начало отсчета совмещаем с поверхностью; ось z направляем по нормали к поверхности. В результате жидкость заполняет верхнее полупространство z ≥ 0. Выполняя интегрирование в цилиндрических координатах, получим уравнение для одночастичного термического потенциала:
(3)
$\begin{gathered} {{\omega }_{1}}\left( {{{z}_{1}}} \right) = \\ = 2\pi n\int\limits_0^\infty {d{{z}_{2}}{{G}_{1}}\left( {{{z}_{2}}} \right)} \int\limits_{\left| {{{z}_{{12}}}} \right|}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( 1 \right)}}\left( {{{r}_{{12}}},{{z}_{1}},{{z}_{2}}} \right) + \mu } , \\ \end{gathered} $(4)
$\begin{gathered} {{\omega }_{1}}\left( {{{z}_{1}}} \right) = 2\pi n\int\limits_{ - {{z}_{1}}}^\infty {d{{z}_{{12}}}{{G}_{1}}\left( {{{z}_{1}} + {{z}_{{12}}}} \right)} \times \\ \times \,\,\int\limits_{\left| {{{z}_{{12}}}} \right|}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( 1 \right)}}\left( {{{r}_{{12}}},{{z}_{1}},{{z}_{2}}} \right)} - \\ - \,\,2\pi n\int\limits_{ - \infty }^\infty {d{{z}_{{12}}}} \int\limits_{\left| {{{z}_{{12}}}} \right|}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( 1 \right)}}\left( {{{r}_{{12}}}} \right)} . \\ \end{gathered} $Выделим во втором слагаемом две области интегрирования: (–∞, –z1) и (–z1, +∞). Используем упоминавшееся выше синглетное приближение и выберем химический потенциал таким образом, что ω1(z1) → 0 при z1 → ∞. После несложных преобразований уравнение примет следующий вид:
(5)
$\begin{gathered} {{\omega }_{1}}\left( {{{z}_{1}}} \right) = 2\pi n\int\limits_0^\infty {d{{z}_{2}}\left( {{{G}_{1}}\left( {{{z}_{2}}} \right) - 1} \right)} \times \\ \times \,\,\int\limits_{\left| {{{z}_{{12}}}} \right|}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( 1 \right)}}\left( {{{r}_{{12}}}} \right)} - \\ - \,\,2\pi n\int\limits_{{{z}_{1}}}^\infty {d{{z}_{{12}}}} \int\limits_{\left| {{{z}_{{12}}}} \right|}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( 1 \right)}}\left( {{{r}_{{12}}}} \right)} . \\ \end{gathered} $Наконец, делая допущение, что для всех значений z1 справедлива аппроксимация ω1(z1) → → ω1(z1) – 1, получаем модифицированное синглетное уравнение:
(6)
$\begin{gathered} {{e}^{{{{{\omega }}_{1}}\left( {{{z}_{1}}} \right)}}} - 1 = 2\pi n\int\limits_0^\infty {d{{z}_{2}}\left( {{{e}^{{{{{\omega }}_{1}}\left( {{{z}_{2}}} \right)}}} - 1} \right)} \times \\ \times \,\,\int\limits_{\left| {{{z}_{{12}}}} \right|}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( 1 \right)}}\left( {{{r}_{{12}}}} \right)} - 2\pi n\int\limits_{{{z}_{1}}}^\infty {d{{z}_{{12}}}} \int\limits_{\left| {{{z}_{{12}}}} \right|}^\infty {{{r}_{{12}}}d{{r}_{{12}}}C_{{12}}^{{\left( 1 \right)}}\left( {{{r}_{{12}}}} \right)} . \\ \end{gathered} $Данное уравнение является линейным интегральным уравнением Фредгольма второго рода и может быть решено аналитически.
ЗАКЛЮЧЕНИЕ
Предложено обобщение синглетного уравнения для молекулярной системы вблизи твердой поверхности в приближении Перкуса–Йевика. Уравнение имеет вид линейного интегрального уравнения Фредгольма второго рода. Для системы твердых сфер уравнение допускает аналитическое решение.
Возможно обобщение данного уравнения на молекулярные системы с реалистичными потенциалами межчастичного взаимодействия, что важно для практических задач материаловедения.
Исследования проведены при частичной поддержке Минобрнауки РФ в рамках выполнения государственного задания РФ (проект № 3.1941.2017/ПЧ).
Список литературы
Nishinaga T. Handbook of crystal growth: fundamentals. Tokyo: Elsevier, 2014. P. 1157.
Termentzidis K. Nanostructured semiconductors: amorphization and thermal properties. Singapore: Jenny Stanford Publ., 2017. 574 p.
Саркисов Г.Н. // УФН. 2002. Т. 172. № 6. С. 647; Sarkisov G.N. // Phys. Usp. 2002. V. 45. № 6. P. 597.
Mézard M., Parisi G. // J. Phys. Cond. Matter. 1999. V. 11. № 10A. P. A157.
Bomont J.-M., Hansen J.-P., Pastore G. // J. Chem. Phys. 2019. V. 150. № 15. Art. № 154504.
Bomont J.-M., Hansen J.-P., Pastore G. // Phys. Rev. E. 2015. V. 92. № 4. Art. № 042316.
Bomont J.-M., Hansen J.-P., Pastore G. // J. Chem. Phys. 2014. V. 141. № 17. Art. № 174505.
Bomont J.-M., Pastore G., Hansen J.-P. // J. Chem. Phys. 2017. V. 146. № 11. Art. № 114504.
Parisi G., Seoane B. // Phys. Rev. E. 2014. V. 89. № 2. Art. № 022309.
Tsednee T., Luchko T. // Phys. Rev. E. 2019. V. 99. № 3. Art. № 032130.
Rogers D.M. // arXiv:1807.05963. 2018.
Tikhonov D.A., Kiselyov O.E., Martynov G.A., Sar-kisov G.N. // J. Mol. Liq. 1999. V. 82. № 1–2. P. 3.
Agrafonov Y., Petrushin I. // Phys. Proc. 2015. V. 71. P. 364.
Agrafonov Y., Petrushin I. // J. Phys. Conf. Ser. 2016. V. 747. № 1. Art. № 012024.
Paganini I.E., Davidchack R.L., Laird B.B., Urrutia I. // J. Chem. Phys. 2018. V. 149. № 1. Art. № 014704.
Kaneyoshi T. // Phys. B. 2017. V. 513. P. 87.
Martynov G.A. Fundamental theory of liquids; method of distribution functions. Bristol, Philadelphia, New York: Adam Hilger, 1992. P. 470.
Wertheim M.S. // Phys. Rev. Lett. 1963. V. 10. № 8. P. 321.
He Y., Rice S.A., Xu X. // J. Chem. Phys. 2016. V. 145. № 23. Art. № 234508.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


