1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 9, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 9, стр. 1265-1268

Моделирование переключения в тонких сегнетоэлектрических пленках

О. С. Баруздина 1, 2, О. Г. Максимова 1, *, А. В. Максимов 1, В. И. Егоров 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования Череповецкий государственный университет
Череповец, Россия

2 Федеральное государственное бюджетное образовательное учреждение высшего образования Воронежский государственный университет
Воронеж, Россия

* E-mail: og62@mail.ru

Поступила в редакцию 10.04.2020
После доработки 29.04.2020
Принята к публикации 27.05.2020

Полный текст (PDF)

Аннотация

Для исследования процессов переключения в тонких сегнетоэлектрических пленках использована модифицированная трехмерная модель Изинга, в которой учтена роль деполяризующего поля. Исследовано влияние толщины пленки и деполяризующего поля на величину коэрцитивного поля и форму кривой диэлектрического гистерезиса.

В ряде тонкопленочных сегнетоэлектрических устройств используется переключение поляризации в направлении, перпендикулярном плоскости пленки, что позволяет при малых ее толщинах управлять поляризацией весьма малыми напряжениями [1]. Особое внимание уделяется пленкам, в которых наблюдается размерный эффект [2]. При этом основные направления теоретических и экспериментальных исследований зависимости поляризации от напряженности внешнего электрического поля P(E) в сегнетоэлектрических тонких пленках сосредоточены на изучении: нарушения динамической симметрии [3, 4], изменения площади петли гистерезиса при изменении толщины пленки [5], наличия внутреннего поля смещения [6]. Экспериментальные исследования показывают, что точка фазового перехода при уменьшении толщины пленки может смещаться как в сторону высоких [7], так и низких температур [8]. В [8] показано, что в некоторых достаточно тонких пленках спонтанная поляризация не наблюдается, т.е. существует критическое значение толщины.

Использование при моделировании “закрепленных” или “свободных” граничных условий в модели Изинга позволяет подтвердить смещение точки Кири к высоким, или низким температурам соответственно. Однако, при моделировании поляризации сегнетоэлектрических тонких пленок без учета деполяризующего поля критической толщины обнаружить не удается. Эту проблему решает учет в модели деполяризующего поля, которое оказывает значительное влияние только для тонких пленок. Показано, что в этом случае при свободных граничных условиях с уменьшением толщины пленки величина поляризации уменьшается, а при определенном критическом значении резко падает до нуля [9]. Включение деполяризующего поля приводит к понижению температуры Кюри.

Целью работы является теоретическое исследование влияния толщины пленки на переключение тонких сегнетоэлектрических пленок.

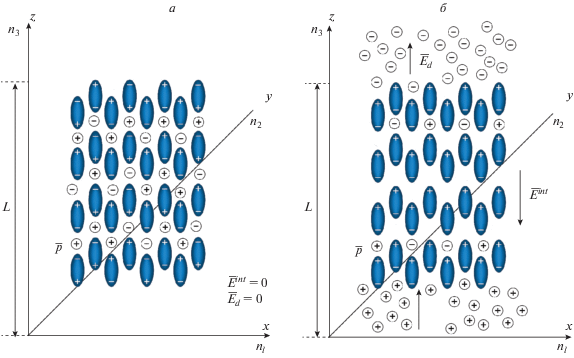
Для изучения переключательных характеристик тонких сегнетоэлектрических пленок и описания их свойств мы используем трехмерную модель Изинга [10, 11], состоящую из N1, N2 и N3 узлов вдоль соответствующих осей декартовой системы координат. Предполагалось, что в поперечном сечении толщиной пленки L содержится N3 элементарных ячеек. Положение узла решетки характеризуются набором трех чисел $\vec {n} = ({{n}_{1}},{{n}_{2}},{{n}_{3}})$ (рис. 1а, 1б).

Рис. 1.

Схематическое изображение электрических диполей (а) и заряженных частиц (б) в пленке.

В данной работе потенциальная энергия одного диполя, расположенного в узле $\vec {n},$ описывается следующей формулой [9]:

(1)
${{U}_{{\vec {n}}}} = - J\sum\limits_{\vec {m}} {{{S}_{{\vec {n}}}}{{S}_{m}} - pE{{S}_{{\vec {n}}}} - p{{S}_{{\vec {n}}}}{{E}_{d}}} ,$
где величина ${{S}_{{\vec {т}}}}$ может принимать два значения +1 и –1, J – энергетическая константа, p – дипольный момент, ${{E}_{d}}$ – напряженность деполяризующего поля. Суммирование производится по ближайшим соседям.

Параметр дальнего ориентационного порядка, который пропорционален поляризации, определяется по следующей формуле [10]:

(2)
$\mu = \frac{1}{{{{N}_{1}}{{N}_{2}}{{N}_{3}}}}\sum\limits_{\vec {n}} {{{S}_{{\vec {n}}}}} .$

Учитывалось, что существуют свободные носители заряда, которые распределены внутри сегнетоэлектрической пленки с определенной плотностью. Введена переменная M, величина которой равна координате z точки (рис. 1а, 1б), в которой плотность положительного заряда максимальна. В отсутствии поля и поляризации распределение плотности заряженных частиц равномерное (рис. 1а), деполяризующее поле отсутствует и поэтому принимается что, $M = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}.$ В поляризованной пленке в отсутствии внешнего поля распределение плотности свободных зарядов неравномерное (рис. 1б). Наибольшая плотность положительного заряда находится на одной из поверхностей пленки, поэтому $M = 0$ или L в зависимости от направления поляризации. Для характеристики наличия деполяризующего поля введена величина β (если $\beta = 1,$ то деполяризующее поле есть, при $\beta = 0$ – деполяризующего поля нет).

При большом значении толщины основная часть частиц не достигает поверхности пленки, поэтому деполяризующее поле отсутствует $\left( {\beta = 0} \right).$ При уменьшении толщины сегнетоэлектрической пленки на ее границах возникает деполяризующее поле $\left( {\beta = 1} \right)$ в определенные интервалы времени. При этом направление деполяризующего поля изменяется в зависимости от того, на какой поверхности располагается максимальное значение плотности положительного заряда. Время, в течение которого существует деполяризующее поле, зависит от подвижности носителей заряда и от толщины пленки.

Для изучения переключательных характеристик тонких сегнетоэлектрических пленок было проведено моделирование по следующему алгоритму:

1) Задаются начальные условия. Проводится расчет диэлектрического состояния пленки только после достаточно большого количества шагов компьютерного моделирования. Поэтому выбор начальных условий является произвольным. Принималась разупорядоченная ориентация диполей. Значение параметра дальнего ориентационного порядка и величины β принимались равными нулю (${{\mu }_{0}} = 0,$ ${{\beta }_{0}} = 0$). Значение величины ${{M}_{0}} = {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2}.$

2) Задается цикл по времени с шагом $\Delta t,$ на k‑ом шаге моделирования:

а) Определение величины M. Заряды перемещались под действием электрического поля:

(3)
$\vec {E} = {{\vec {E}}^{{ext}}} + {{\vec {E}}^{{{\text{int}}}}},$
где ${{\vec {E}}^{{{\text{int}}}}}$ – внутреннее электрическое поле, вызванное спонтанной поляризацией, определяется формулой (4):
(4)
$\vec {Е}_{k}^{{int}} = {{\mu }_{{k - 1}}}\alpha ,$
где α – коэффициент пропорциональности.

${{\vec {E}}^{{ext}}}$ – внешнее поле с частотой ω, которое определяется следующим образом:

(5)
${{\vec {E}}^{{ext}}}_{k} = {{\vec {E}}_{0}}\cos (\omega (k\Delta t)).$

Средняя скорость движения потока заряженных частиц определяется по формуле:

(6)
$\left\langle \upsilon \right\rangle = \lambda E(t),$
где λ – подвижность носителей заряда.

Для определения распределения зарядов внутри пленки решалось уравнение Смолуховского:

(7)
$\frac{{\partial \rho }}{{\partial t}} = - \frac{{\partial \left\langle \upsilon \right\rangle \rho }}{{\partial z}},$
где ρ – плотность заряда.

При решении уравнения (7) использовались граничные условия Неймана:

(8)
${{\left. {\frac{{\partial \rho }}{{\partial z}}} \right|}_{{z = 0}}} = {{\left. {\frac{{\partial \rho }}{{\partial z}}} \right|}_{{z = L}}} = 0.$

Затем определялась величина М как максимум функции ρ(z).

б) Вычисление деполяризующего поля. Напряженность деполяризующего поля выражается формулой (9):

(9)
${{Е}_{{d,k}}} = {{Е}_{{d0}}}{{\beta }_{k}}\left( {{{e}^{{ - {\delta }({{N}_{3}} - {{n}_{3}})}}} + {{e}^{{ - {\delta }({{n}_{3}} - 1)}}}} \right),$
где ${{E}_{{d0}}}$ и δ – постоянные, определяемые числом свободных носителей.

в) с помощью метода Монте-Карло (алгоритм Метрополиса) вычислялась поляризация. Потенциальная энергия определялась по формуле (1). Вычислялось значение параметра порядка ${{\mu }_{k}}.$ Алгоритм этой процедуры рассмотрен в [12].

3) Построение зависимости параметра порядка от напряженности электрического поля. Для ограничения влияния начальных условий кривые гистерезиса вычислялись после пятого цикла по поляризации.

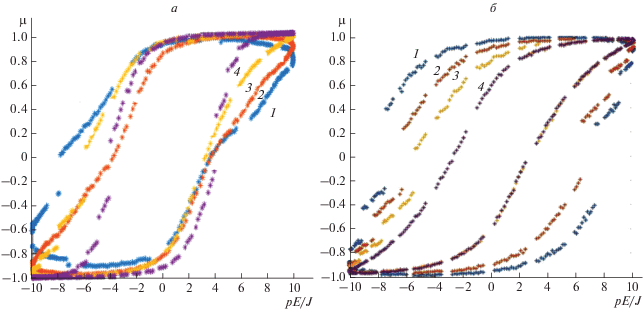
Для данной модели были вычислены зависимости параметра дальнего ориентационного порядка от напряженности общего электрического поля µ(E). Внутреннее поле вычислялось с учетом деполяризующего поля с помощью модели Изинга. Приведены зависимости µ(E) при различных значениях частоты (рис. 2а) и толщины сегнетоэлектрической пленки (рис. 2б). Учет частоты ω внешнего электрического поля производился следующим образом: величина ω должна быть обратно пропорциональной числу шагов Монте-Карло ${{N}_{{{\text{MK}}}}}$ [13]. В качестве эталонной частоты в работе было принято значение ${{\omega }_{r}},$ соответствующее числу шагов Монте-Карло ${{N}_{{{\text{MK}}}}} = 10$ на одну частицу. Влияние частоты на вид петель гистерезиса для объемного сегнетоэлектрика было рассмотрено, например, в работе [14]. Результаты моделирования показали, что для тонких сегнетоэлектрических пленок (в отличии от объемного) при увеличении значения частоты наблюдается нарушение симметрии. На рис. 2а, 2б видно, что петля смещена относительно центра по горизонтальной оси при увеличении частоты и уменьшении толщины пленки, что является свидетельством наличия внутреннего поля смещения, которое увеличивается с уменьшением толщины.

Рис. 2.

Зависимость параметра дальнего ориентационного порядка $\mu $ от величины внешнего электрического поля ${{pE} \mathord{\left/ {\vphantom {{pE} J}} \right. \kern-0em} J}$ при различных значениях частоты ${\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{r}}}}} \right. \kern-0em} {{{\omega }_{r}}}}$ = 7 (1), 5 (2), 3 (3), 1 (4) с толщиной $L = 15a$ (а) и толщины сегнетоэлектрической пленки $L$ = 7а (1), 10а (2), 15а (3), 20а (4) с частотой ${\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{r}}}}} \right. \kern-0em} {{{\omega }_{r}}}} = 3$ (б) при различных значениях приведенной температуры ${{{{k}_{B}}T} \mathord{\left/ {\vphantom {{{{k}_{B}}T} J}} \right. \kern-0em} J}$ = 5 (а), 7 (б), p – дипольный момент, a – размер элементарной ячейки.

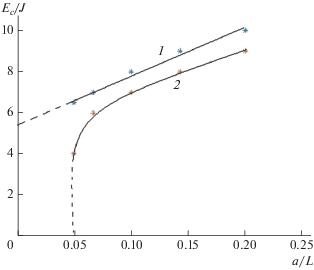
На рис. 3 приведена зависимость коэрцитивного поля от обратной толщины сегнетоэлектрической пленки. Ниже точки фазового перехода в объемном сегнетоэлектрике график имеет линейную зависимость (кривая 1 на рис. 3), что согласуется с экспериментальными данными [15]. При увеличении толщины пленки при определенном значении происходит резкое падение значения коэрцитивного поля (кривая 2 на рис. 3).

Рис. 3.

Зависимость коэрцитивного поля ${{{{E}_{c}}} \mathord{\left/ {\vphantom {{{{E}_{c}}} J}} \right. \kern-0em} J}$ от обратной толщины тонкой сегнетоэлектрической пленки ${a \mathord{\left/ {\vphantom {a L}} \right. \kern-0em} L}$ при различных значениях приведенной температуры ${{{{k}_{B}}T} \mathord{\left/ {\vphantom {{{{k}_{B}}T} J}} \right. \kern-0em} J}$ = $2(1),5(2).$

Предложенная модель позволяет получить зависимость коэрцитивного поля от толщины пленки. Коэрцитивное поле определяется величиной деполяризующего поля, которое возникает в тонких сегнетоэлектрических пленках за счет миграции заряженных частиц в переменных электрических полях.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 19-32-50032).

Список литературы

  1. Сигов А.С., Мишина Е.Д., Мухортов В.М. // ФТТ. 2010. Т. 52. № 4. С. 709; Sigov A.S., Mishina E.D., Mukhortov V.M. // Phys. Sol. St. 2010. V. 52. № 4. P. 762.

  2. Блинов Л.М., Фридкин В.М., Палто СП. и др. // УФН. 2000. Т. 170. № 3. С. 247; Blinov L.M., Fridkin V.M., Palto S.P. et al. // Phys. Usp. 2000. V. 43. № 3. P. 243.

  3. Acharyya M. // Phys. Rev. E. 2004. V. 69. № 2. Art. № 027105.

  4. Jang H., Grimson M.J., Hall C.K. // Phys. Rev. B. 2003. V. 67. Art. № 094411.

  5. Zhu H., Dong S., Liu J.-M. // Phys. Rev. B. 2004. V. 70. Art. № 132403.

  6. Даринский Б.М., Сидоркин А.С., Нестеренко Л.П. и др. // ФТТ. 2015. Т. 57. № 3. С. 536; Darinskiy B.M., Sidorkin A.S., Nesterenko L.P. et al. // Phys. Sol. St. 2015. V. 57. № 3. P. 3549.

  7. Сидоркин А.С., Нестеренко Л.П., Сидоркин А.А. // Матер. “INTERMATIC–2016”. Ч. 2. (Москва, 2016). С. 86.

  8. Paul J., Nishimatsu T., Kawazoe Y. et al. // Phys. Rev. Lett. 2007. V. 99. Art. № 077601.

  9. Maksimova O.G., Baruzdina O.S., Maksimova E.A. // J. Phys. Conf. Ser. 2017. V. 936. Art. № 012042.

  10. Baxter R.J. Exactly solved models in statistical mechanics. London: Academic Press, 1982. 498 p.

  11. Lundow P.H., Markstrom K., Rosengren A. // Phil. Mag. 2009. V. 89. P. 2009.

  12. Gould H., Tobochnik J., Harrison D. // An introduction to computer simulation methods: applications to physical systems. Part 2. N.Y.: Addison-Wesley, 1988.

  13. Биндер К., Хеерман Д.В. Моделирование методом Монте-Карло в статистической физике. М.: Наука, 1995. 142 с.

  14. Максимова О.Г., Петрова Т.О., Максимов А.В. // Изв. РАН. Сер. физ. 2013. Т. 77. № 8. С. 1177; Maksimova O.G., Petrova T.O., Maksimov A.V. // Bull. Russ. Acad. Sci. Phys. 2013. V. 77. № 8. P. 1068.

  15. Сидоркин А.С., Сигов А.С., Хохлов А.М. и др. // ФТТ. 2000. Т. 42. № 4. С. 727; Sidorkin A.S., Sigov A.S., Khokhlov A.M. et al. // Phys. Sol. St. 2000. V. 42. № 4. P. 745.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал