Известия РАН. Серия физическая, 2020, T. 84, № 9, стр. 1261-1264
Временная эволюция электрической энергии кристалла Rb2ZnCl4 как функция поляризации в сегнетоэлектрической фазе вблизи точки Кюри
В. В. Горбатенко 1, *, Б. Н. Прасолов 2, С. А. Горбатенко 3, Н. В. Даценко 4
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Воронежский государственный технический университет”
Воронеж, Россия
2 Общество с ограниченной ответственностью “Инвестиции и технологии”
Воронеж, Россия
3 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Воронежский государственный институт физической культуры”
Воронеж, Россия
4 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Воронежский государственный университет инженерных технологий”
Воронеж, Россия
* E-mail: vlgorbatenko@mail.ru
Поступила в редакцию 10.04.2020
После доработки 29.04.2020
Принята к публикации 27.05.2020
Аннотация
Методом гармонического анализа изучен процесс переполяризации кристалла Rb2ZnCl4 под действием гармонического электрического поля в сегнетоэлектрической фазе вблизи температуры Кюри. Исследование гармоник плотности тока позволило построить зависимость плотности электрической энергии ${{W}_{C}}$ от измеренной в динамике поляризации ${{P}_{C}},$ и изучить временную эволюцию этой зависимости после выведения доменной структуры из положения равновесия переменным электрическим полем. Установлено, что во время релаксации происходит значительное изменение характера указанной зависимости.
Известен ряд работ, которые посвящены исследованию нелинейного диэлектрического отклика, обусловленного отрывом доменных границ (ДГ) от дефектов кристаллической решетки [1–4] в сегнетоэлектрических материалах. В результате проведенных экспериментов установлено, что исследование спектральных составляющих поляризации $\left( {{{P}_{x}}} \right),$ диэлектрической проницаемости $\left( {{{{\varepsilon }}_{x}}} \right)$ и тангенса угла диэлектрических потерь (tg) позволяет проследить основные закономерности доменной динамики в переменном электрическом поле, что свидетельствует о перспективности гармонического анализа как метода изучения механизмов процесса переполяризации.
На основании диэлектрических и поляризационных исследований на образцах кристаллов Rb2ZnCl4 было показано [5, 6], что релаксация неравновесных ${{{\varepsilon }}_{x}}$ и tg выше температуры сегнетоэлектрического фазового перехода (${{T}_{C}}$ ≈ 199.4 К) связана с откреплением сегнетоэлектрических доменных границ от стопоров и последующим исчезновением доменной структуры в несоразмерной фазе (НФ). Обращает на себя внимание, что в равновесных условиях в окрестности TC в сегнетоэлектрической фазе (СФ) имеет место температуронезависимое поведение поля насыщения $\left( {{{E}_{k}}} \right)$ [6], обнаруженное путем анализа петель диэлектрического гистерезиса, измеренных на частоте 0.3 Гц. В [7] методом гармонического анализа процесса переполяризации кристаллов Rb2ZnCl4 из величины напряженности ${{E}_{k}}$ выделены две составляющие: ${{E}_{c}}$ и ${{E}_{0}}.$ Составляющая ${{E}_{c}},$ называемая коэрцитивным полем, обусловлена потерями, возникающими в образце, т.е., когда напряженность электрического поля, приложенного к образцу, становится равной величине ${{E}_{c}},$ поляризация ${{P}_{x}}(t)$ достигает нулевого значения. Величина напряженности поля переключения ${{E}_{0}} = {{E}_{k}} - {{E}_{с}}$ соответствует величине напряженности поля, которую нужно добавить к ${{E}_{c}},$ чтобы обеспечить практически полную монодоменизацию исследуемого образца. При напряженностях измерительного электрического поля ${{E}_{m}} > {{E}_{k}}$ величины напряженности ${{E}_{0}}$ и ${{E}_{c}}$ остаются практически неизменными.
В работах [5–8] было показано, что, если при изотермической выдержке образцов кристаллов Rb2ZnCl4 в СФ подключить переменное электрическое поле $\left( {{{E}_{ \sim }}} \right)$ с частотой порядка 20 кГц и амплитудой выше ${{E}_{k}},$ то после отключения ${{E}_{ \sim }}$ наблюдаются релаксации ${{{\varepsilon }}_{x}}$ и ${{E}_{k}}.$ “Электрополевой отжиг” приводит к уменьшению ${{E}_{k}},$ что подтверждает процесс освобождения ДГ от дефектов. После выключения ${{E}_{ \sim }}$ происходит увеличение ${{E}_{k}},$ т.е. обратный процесс – процесс закрепления ДГ дефектами. В работе [8] была изучена временная эволюция петель диэлектрического гистерезиса методом гармонического анализа после воздействия на образец ${{E}_{ \sim }}.$ Анализ временной эволюции петель диэлектрического гистерезиса показал, что имеет место релаксация величины напряженности поля ${{E}_{c}},$ а значение напряженности поля переключения ${{E}_{0}}$ остается практически неизменным. Временная зависимость ${{E}_{c}}$ достаточно хорошо аппроксимируется выражением:
(1)
${{E}_{c}}(t) = {{E}_{\infty }} - {{E}_{{cо}}}\exp ( - \sqrt {{t \mathord{\left/ {\vphantom {t {{{{\tau }}_{1}}}}} \right. \kern-0em} {{{{\tau }}_{1}}}}} ),$На основе изучения динамики процессов переполяризации в кристаллах группы A2BX4 в СФ в окрестности температуры фазового перехода ${{T}_{C}}$ в работе [9], согласно теории Ландау–Гинзбурга–Девоншира, была построена статическая зависимость плотности электрической энергии $\left( {{{W}_{c}}} \right)$ от поляризации $\left( {{{P}_{c}}} \right),$ обусловленной емкостной плотностью тока.
Цель настоящей работы – исследование временной эволюции формы рельефа зависимости ${{W}_{c}}({{P}_{c}})$ в процессе релаксации доменной структуры после выведения ее из состояния равновесия переменным электрическим полем ${{E}_{ \sim }}$ при изотермической выдержке образцов кристаллов Rb2ZnCl4 в СФ вблизи ${{T}_{C}}.$
Для построения на экране монитора компьютера петли диэлектрического гистерезиса использовалась схема, состоящая из двух последовательно включенных относительно источника гармонического напряжения элементов: измерительного образца Х, импеданс которого Zx, и эталонного токового резистора Rэт, сопротивление которого удовлетворяет условию R $ \ll $ |Zx|. Напряжение, возникающее на Rэт, которое пропорционально протекающему через исследуемый образец периодическому току сложной формы, и напряжение, приложенное к исследуемому образцу, оцифровывались в реальном масштабе времени. При помощи пакета прикладных программ Mathcad оцифрованные временные зависимости напряжения, пропорциональные току, протекающему через исследуемый образец, были представлены рядом Фурье.
Эквивалентная электрическая схема замещения исследуемого образца имеет вид параллельного включенных емкости ${{C}_{x}}$ и проводимости ${{G}_{x}},$ обусловленной диэлектрическими потерями. В образцах при приложения к ним переменного электрического поля $E(t) = {{E}_{m}}\sin {{\omega }_{{\text{0}}}}t$ частотой ${{{\omega }}_{{\text{0}}}}$ и амплитудой ${{E}_{m}},$ достаточной для полной монодоменизации образца, возникает ток сложной периодической формы, плотность которого описывается рядом Фурье:
(2)
${{J}_{x}}(t) = \sum\limits_{k = 1}^\infty {{{J}_{k}}\cos (k{{\omega }_{{\text{0}}}}t - \left| {{{\varphi }_{k}}} \right|)} ,$Зависимость ${{J}_{x}}(t)$ включает в себя две составляющие: ${{J}_{c}}(t)$ и ${{J}_{g}}(t).$ Первая составляющая ${{J}_{c}}(t)$ = = $\sum\nolimits_{k = 1}^\infty {{{J}_{k}}\cos {{\varphi }_{k}}\cos k{{\omega }_{0}}t} $ обусловлена емкостной плотностью тока, вторая составляющая ${{J}_{g}}(t)$ = = $\sum\nolimits_{k = 1}^\infty {{{J}_{k}}\sin {{\varphi }_{k}}\sin k{{\omega }_{{\text{0}}}}t} $ обусловлена током проводимости. Временная зависимость общей плотности тока ${{J}_{x}}(t)$ = ${{J}_{c}}(t) + {{J}_{g}}(t)$ приводит к временной зависимости поляризации ${{P}_{x}}(t),$ возникающей в исследуемом образце. Зависимость ${{P}_{x}}(t),$ имеющая две составляющие ${{P}_{c}}(t)$ и ${{P}_{g}}(t),$ описывается выражением:
(3)
${{P}_{x}}(t) = \sum\limits_{k = 1}^\infty {{{P}_{k}}\sin (k{{\omega }_{{\text{0}}}}t - {{\varphi }_{k}})} ,$Составляющая ${{P}_{c}}(t)$ = $\sum\nolimits_{k = 1}^\infty {{{P}_{k}}\cos {{\varphi }_{k}}\sin k{{\omega }_{{\text{0}}}}t} ,$ обусловленная емкостной плотностью тока ${{J}_{c}}(t),$ соответствует временной зависимости поляризации исследуемого образца. Вторая составляющая ${{P}_{g}}(t)$ = $\sum\nolimits_{k = 1}^\infty {{{P}_{k}}\sin {{\varphi }_{k}}\cos k{{\omega }_{{\text{0}}}}t} $ обусловлена плотностью тока ${{J}_{g}}(t),$ т.е. вкладом в поляризацию диэлектрических потерь, преимущественно вызванных затратами энергии на переключение поляризации.
Достоверность результатов эксперимента контролировалась одновременной регистрацией 32 гармоник напряжения, возникающего на эталонном конденсаторе, схема Сойера–Тауэра [10], методом параллельного гармонического анализа [11] действительных и мнимых составляющих плотности тока или поляризации при воздействии на образец гармонического напряжения. Схема установки, реализующей указанную методику, подробно описана в [12].
Таким образом, после измерения амплитуд гармоник ${{J}_{k}}$ и соответствующих им углов ${{\varphi }_{k}},$ обработка результатов измерений программным путем обеспечивает построение временных зависимостей ${{J}_{x}}(t),$ ${{J}_{c}}(t),$ ${{J}_{g}}(t),$ ${{P}_{x}}(t),$ ${{P}_{c}}(t)$ и ${{P}_{g}}(t).$ Возможность ввода или удаления при синтезе отдельных спектральных составляющих поляризаций или плотностей тока позволяет оценивать их влияние на формы получаемых зависимостей, что расширяет возможности интерпретации результатов измерений, полученных ранее другими способами.
В [9] было показано, что плотность электрической энергии ${{W}_{o}}(t),$ забираемой из источника внешнего электрического поля $E(t)$ = ${{E}_{m}}\sin {{\omega }_{0}}t$ определяется выражением:
(4)
${{W}_{o}}(t) = {{P}_{c}}(t){{E}_{m}}\sin {{\omega }_{0}}t - {{P}_{g}}(t)tg({{\varphi }_{1}}){{E}_{m}}\cos {{\omega }_{0}}t.$Плотность энергии ${{W}_{E}}{\text{(}}t{\text{),}}$ затрачиваемая на создание гармонического поля $E(t)$ = ${{E}_{m}}\sin {{\omega }_{0}}t,$ приложенного к образцу, определяется выражением:
(5)
$\begin{gathered} {{W}_{E}}{\text{(}}t{\text{)}} = \int\limits_0^t {{{P}_{c}}{\text{(}}t{\text{)}}{{\omega }_{0}}{{E}_{m}}{\text{cos(}}{{{\omega }}_{0}}t{\text{)}}dt} + \\ + \,\,\int\limits_0^t {{{P}_{g}}{\text{(}}t{\text{)tg(}}{{\varphi }_{1}}{\text{)}}{{\omega }_{0}}{{E}_{m}}{\text{sin(}}{{\omega }_{0}}t{\text{)}}dt} = \frac{{{{P}_{1}}}}{{2{{\omega }_{0}}}} \times \\ \times \,\,\left( {{\text{cos(}}{{{\varphi }}_{{\text{1}}}}{\text{)}}\,{\text{ + }}\,{\text{tg(}}{{{\varphi }}_{{\text{1}}}}{\text{)sin(}}{{{\varphi }}_{{\text{1}}}}{\text{)}}} \right)\left[ {1 - {\text{cos}}2{{\omega }_{0}}t} \right] + \tfrac{{{{\omega }_{0}}{{E}_{m}}}}{2} \times \\ \times \,\,\sum\limits_{k = 3}^\infty {\left[ {\frac{{{{P}_{k}}}}{{{\text{(}}k - 1{\text{)}}{{\omega }_{0}}}}{\text{(cos(}}{{\varphi }_{k}}{\text{)}} - {\text{tg(}}{{\varphi }_{1}}{\text{)sin(}}{{\varphi }_{k}}{\text{))}} \times } \right.} \\ \times \,\,\left[ {1 - {\text{cos((}}k - 1{\text{)}}{{\omega }_{0}}t} \right] + \frac{{{{P}_{k}}}}{{{\text{(}}k + 1{\text{)}}{{\omega }_{0}}}}{\text{(cos(}}{{\varphi }_{k}}{\text{)}} + \\ + \,\,\left. {_{{_{{_{{_{{_{{}}}}}}}}}}^{{^{{^{{}}}}}}{\text{tg(}}{{\varphi }_{1}}{\text{)sin(}}{{\varphi }_{k}}{\text{))[}}1 - {\text{cos((}}k + 1{\text{)}}{{\omega }_{0}}t)]} \right]{\text{.}} \\ \end{gathered} $Таким образом, плотность электрической энергии ${{W}_{c}}(t)$ образца равна:
Построение зависимости ${{W}_{c}}({{P}_{c}})$ осуществлялось путем синтеза зависимости ${{W}_{c}}(t)$ от ${{P}_{c}}(t)$ при помощи пакета прикладных программ Mathcad.
Построение полевых зависимостей ${{P}_{x}}(E),$ ${{P}_{c}}(E)$ и ${{P}_{g}}(E)$ осуществлялось путем синтеза зависимостей ${{P}_{x}}(t),$ ${{P}_{c}}(t)$ и ${{P}_{g}}(t)$ от $E(t).$
Кристаллы Rb2ZnCl4 были выращены методом Чохральского. Измерения проводились на образцах Х-среза в форме прямоугольных пластин размером 7 × 5 × 0.5 мм3 с напыленными серебряными электродами.
Известно, что особенности поведения диэлектрических и поляризационных свойств кристалла Rb2ZnCl4 в сегнетоэлектрической фазе в интервале температур от точки Кюри ${{T}_{C}}$ до T* ≈ 150 К определяются динамикой как сегнетоэлектрических доменных границ, так и солитонов, а величины их вкладов существенно зависят от предыстории кристалла и, в частности, от температуры и времени выдержки образцов в параэлектрической и несоразмерной фазах [9, 10].
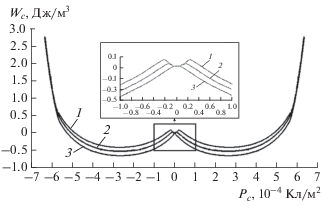
Рис. 1.
Временная эволюция формы потенциального рельефа зависимости ${{W}_{c}}({{P}_{c}}),$ снятых в установившемся режиме (кривая 1), через 10 с после отключения ${{E}_{ \sim }}$ (кривая 2) и сразу же после отключения ${{E}_{ \sim }}$ (кривая 3).
Для того, чтобы избавиться от вклада в диэлектрические и поляризационные свойства кристалла динамики солитонной структуры, эксперимент проводился следующим образом. Сначала образец охлаждался ниже T* на 20 К, где, как было установлено в [10], солитонная структура исчезает практически полностью, затем нагревался до T = TC – 2.5 K и, при изотермической выдержке исследуемого образца, проводились измерения амплитуд гармоник тока ${{J}_{k}}$ и соответствующих им углов ${{\varphi }_{k}}.$ При этом к обкладкам исследуемого образца приложено гармоническое электрическое поле $E(t)$ частотой f0 = 0.3 Гц и амплитудой Em = 1.6 ⋅ 105 В/м, выше поля насыщения ${{E}_{k}}.$ Измерения ${{J}_{k}}$ и ${{\varphi }_{k}}$ проводились после выведения доменной структуры из положения равновесия полем ${{E}_{ \sim }}$ с частотой 20 кГц и амплитудой выше ${{E}_{k}}.$
Экспериментально установлено, что в процессе релаксации доменной структуры амплитуды гармоник ${{P}_{k}}$ остаются постоянными, а соответствующие им углы ${{\varphi }_{k}}$ увеличиваются после отключения ${{E}_{ \sim }}.$ Временные зависимости ${{\varphi }_{k}}$ достаточно хорошо аппроксимируются выражением:
(7)
${{{\varphi }}_{k}}(t) = {{{\varphi }}_{{k\infty }}} - {{{\varphi }}_{{ko}}}\exp ( - \sqrt {{t \mathord{\left/ {\vphantom {t {{{{\tau }}_{2}}}}} \right. \kern-0em} {{{{\tau }}_{2}}}}} ),$Время релаксации ${{{\tau }}_{1}}$ напряженности поля ${{E}_{c}}$ по величине равно ${{{\tau }}_{2}}$ – времени релаксации ${{{\varphi }}_{k}}.$ Данный факт подтверждает справедливость определения ${{E}_{c}}$ [7], действительно:
(8)
$\begin{gathered} {{E}_{c}}(t) = {{U}_{m}}\sin ({{{\varphi }}_{1}}(t)) = \\ = {{U}_{m}}\sin ({{{\varphi }}_{{1\infty }}} - {{{\varphi }}_{{1o}}}\exp ( - \sqrt {{t \mathord{\left/ {\vphantom {t {{{{\tau }}_{2}}}}} \right. \kern-0em} {{{{\tau }}_{2}}}}} )). \\ \end{gathered} $При малых значениях ${{\varphi }_{{1o}}}$ будет иметь место выражение (3), при условии, что:
Результаты эксперимента подтверждают справедливость выражений (9) и (10).
На рис. 1 показана временная эволюция формы потенциального рельефа ${{W}_{c}}({{P}_{c}}).$ Зависимости ${{W}_{c}}({{P}_{c}})$ сняты в установившемся режиме (кривая 1), через 10 с после отключения ${{E}_{ \sim }}$ (кривая 2) и сразу же после отключения ${{E}_{ \sim }}$ (кривая 3).
Из анализа временной зависимости ${{W}_{c}}({{P}_{c}})$ следует, что форма потенциального рельефа зависимости ${{W}_{c}}({{P}_{c}})$ соответствует теории Ландау-Гинзбурга–Девоншира, то есть имеют место два минимума ${{W}_{c}}({{P}_{c}})$ сразу же после отключения ${{E}_{ \sim }}$ (кривая 3). В процессе релаксации доменной структуры, после выведения ее из положения равновесия полем ${{E}_{ \sim }},$ на зависимости ${{W}_{c}}({{P}_{c}})$ появляется третий минимум при ${{P}_{c}}{\text{(}}t{\text{)}} = 0.$ Чем больше диэлектрические потери, связанные с увеличением ${{E}_{c}}$ и ${{\varphi }_{k}},$ тем более явно он проявляется.
На основании результатов экспериментов, проведенных при исследовании релаксации доменной структуры образца кристалла Rb2ZnCl4, после выведения ее из положения равновесия полем ${{E}_{ \sim }},$ можно сделать следующие выводы:
1. Амплитуды гармоник поляризации ${{P}_{k}}$ остаются постоянными;
2. Имеет место релаксация только ${{\varphi }_{k}},$ которая приводит к релаксации ${{E}_{c}};$
3. Появление третьего минимума на зависимости ${{W}_{c}}({{P}_{c}})$ при ${{P}_{c}}{\text{(}}E{\text{)}} = 0$ связано с увеличением диэлектрических потерь, обусловленных закреплением доменных границ дефектами.
Список литературы
Федосов В.Н., Сидоркин А.С. // ФТТ. 1977. Т. 19. № 6. С. 1632.
Kamysheva L.N., Drozhdin S.N. // Ferroelectrics. 1989. V. 96. P. 301.
Shil’nikov A.V., Nesterov V.N., Burkhanov A.I. // Ferroelectrics. 1996. V. 175. P. 145.
Карпов А.И., Поплавко Ю.М. // Изв. АН СССР. Сер. физ. 1984. Т. 48. № 6. С. 1193.
Gridnev S.A., Gorbatenko V.V., Prasolov B.N. // Ferroelectrics. 1993. V. 143. № 1–4. P. 85.
Гриднев С.А., Горбатенко В.В., Прасолов Б.Н. // Изв. РАН. Сер. физ. 1993. Т. 57. № 3. С. 97.
Горбатенко В.В., Кудряш В.И., Прасолов Б.Н., Горбатенко С.А. // Изв. РАН. Сер. физ. 2011. Т. 75. № 10. С. 1394; Gorbatenko V.V., Kudryash V.I., Prasolov B.N., Gorbatenko S.A. // Bull. Russ. Acad. Sci. Phys. 2011. V. 75. № 10. P. 1313.
Prasolov B.N., Gorbatenko V.V., Safonova I.A. // Ferroelectrics. 1996. V. 186. P. 231.
Горбатенко В.В., Прасолов Б.Н., Горбатенко С.А. // Изв. РАН. Сер. физ. 2019. Т. 83. № 9. С. 1184; Gorbatenko V.V., Prasolov B.N., Gorbatenko S.A. // Bull. Russ. Acad. Sci. Phys. 2019. V. 83. № 9. P. 1077.
Kretschmer R., Binder K. // Phys. Rev. 1979. B. 20. P. 1065.
Харкевич А.А. Спектры и анализ. М.: ГИФМЛ, 1962. 288 с.
Горбатенко В.В., Прасолов Б.Н., Кудряш В.И., Горбатенко С.А. // Изв. РАН. Сер. физ. 2010. Т. 74. № 9. С. 1294; Gorbatenko V.V., Prasolov B.N., Kud-ryash V.I., Gorbatenko S.A. // Bull. Russ. Acad. Sci. Phys. 2010. V. 74. № 9. P. 1240.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


