Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 14-21

ВВЕДЕНИЕ

В настоящее время голографический метод создания наноразмерных периодических дифракционных структур ДС вызывает особый интерес у исследователей, в связи с возможностью их применения в области оптической связи и обработки информации [1–4]. Свойства объемных пропускающих и отражательных фазовых голографических решеток уже изучены различными коллективами исследователей, и показали, что такие решетки имеют большую дифракционную эффективность, а также высокую угловую и спектральную селективность. В связи с этим поиск новых материалов, перспективных с точки зрения формирования в них подобных структур и управления их оптическими свойствами, представляется весьма актуальным. Все более широкое применение находят фотополимеризующиеся материалы (ФПМ).

Многослойные структуры представляют собой несколько объемных решеток, разделенных оптически однородными промежуточными слоями [5, 6]. Такие структуры характеризуются особыми свойствами, обусловленными интерференцией волн, восстановленных из каждой решетки, и предоставляют возможность управления видом селективного отклика. Многослойные голографические структуры имеют перспективу найти широкое применение в качестве элементов спектральных фильтров, сенсоров, межсоединений, мультиплексоров/демультиплексоров в оптических линиях связи [7, 8].

В работах [5, 8–11] представлены модели дифракции плоских волн на многослойных дифракционных структурах, которые учитывают лишь определенный вид неоднородности профиля показателя преломления или не учитывают его совсем. Однако при решении задачи записи голографических дифракционных структур (ГДС), в том числе и многослойных, в фотополимерных материалах, было установлено, что амплитуда пространственных профилей показателя преломления в процессе записи может быть существенно неоднородной, как показано в [3].

В данной работе исследуется взаимодействие квазимонохроматических световых пучков с многослойной неоднородной голографической фотополимерной дифракционной структурой (МНГДС).

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Рассмотрим процесс считывания МНГДС произвольно поляризованным квазимонохроматическим световым пучком ${{E}^{0}}(\vec {r},t)$ в пренебрежении остаточным поглощением ФПМ.

Для данной модели принято, что дифракция световых пучков происходит на структурах, для которых закончились все процессы записи (весь мономер израсходован), т.е. падающий пучок не может изменить пространственный профиль показателя преломления структуры. Также, что апертура считывающего пучка w $ \gg $ d, где d – толщина одного слоя МНГДС. Состояние поляризации считывающего излучения однородно по апертуре.

Таким образом, процессы дифракции будут описываться в геометрооптическом приближении. Эффекты рассеяния оптического излучения в материале также приняты пренебрежимо малыми, для выполнения данного приближения рассматриваются образцы малой толщины (30–100 мкм). Рассмотрена дифракция только на основной пространственной гармонике показателя преломления ГДС, т.к. амплитуды высших гармоник экспоненциально убывают с увеличением их номера. При этом приведенный подход к описанию дифракции аналогичен для высших пространственных гармоник с заменой соответствующих амплитуд и углов дифракции.

Пусть произвольно поляризованный квазимонохроматический световой пучок, с амплитудным профилем ${{E}^{0}}(\omega ,\vec {r}),$ волновым вектором ${{\vec {k}}^{0}}$ и единичным комплексным вектором поляризации ${{\vec {e}}^{0}},$ падает на возмущенную наклонную дифракционную структуру в области ФПМ образца под произвольным углом к оси y (рис. 1). Тогда, падающую квазиплоскую световую волну на границе раздела сред (у = 0) можно представить в виде суммы линейно-поляризованных пучков c взаимно ортогональными s и p поляризациями:

где ${{\omega }_{0}}$ – центральная частота; $\vec {e}_{0}^{m}$ – единичный вектор поляризации; (m = s, p, индекс s соответствует волне поляризованой перпедикулярно плоскости дифракции YZ, индекс p соответствует волне поляризованой в плоскости плоскости дифракции YZ); $E_{0}^{m}(\omega ,\vec {r})$ = $\left( {{{{\vec {e}}}^{0}} \cdot \vec {e}_{0}^{m}} \right){{E}^{0}}(\omega ,\vec {r})$ – пространственное распределение комплексной амплитуды частотной Фурье-компоненты.

Геометрия дифракции на МНГДС представлена на рис. 1. ${{E}^{0}}$ – падающий (считывающий пучок). $E_{0}^{n},$ $E_{1}^{n}$ прошедший и дифрагировавший в первый порядок пучки.

Рассмотрим дифракцию на n-ом слое МНГДС, распределение дифрагирующих пучков на выходе которой, зависит от распределения дифрагирующих пучков на выходе предыдущего слоя.

Световое поле $\vec {E}$ в каждом слое ГДС в силу дифракции считывающего пучка ${{\vec {E}}^{0}}$ (1) на пространственных гармониках решетки можно записать в виде суммы волн нулевого и первого порядков дифракции:

каждый из которых представлен двумя составляющими вектора напряженности ${{\vec {E}}_{j}}$ в соответствующем ортогональном поляризационном базисе, заданном двумя ортами $\vec {e}_{j}^{p}$ и $\vec {e}_{j}^{s},$ лежащими в плоскости, перпендикулярной оси пучка ${{\vec {E}}_{j}}$. Здесь $E_{j}^{m}(\omega ,\vec {r})$ – медленно меняющиеся функции координат и находятся из уравнений первого приближения медленно меняющихся амплитуд (ММА). j = 0 соответствует проходящему пучку, j = 1 – дифрагированному пучку на решетке с ${{\vec {K}}_{j}}$ = j ⋅ ${{\vec {K}}_{1}}$.

Напряженность электрического поля $E(\vec {r},t)$ в области взаимодействия описывается векторным волновым уравнением, следующим из уравнений Максвелла [12, 13]:

где возмущение диэлектрической проницаемости ε представляется в виде: где ${{\varepsilon }_{0}} = n_{{{\text{st}}}}^{2} \cdot {\mathbf{\hat {{\rm I}}}}$ – невозмущенный тензор диэлектрической проницаемости, $n_{1}^{'}(\vec {r})$ – определяются полученными решениями для процесса записи ГДС [14], ${\mathbf{\hat {{\rm I}}}}$ – единичный тензор, $n_{0}^{'}(\vec {r})$ – амплитуда нулевой гармоники показателя преломления, $\Delta \varepsilon $ – амплитуда основной гармоники возмущения тензора диэлектрической проницаемости, обусловленного записью. ${{n}_{{{\text{st}}}}}$ – показатель преломления ФПМ до формирования.

Следуя методу ММА, в рассматриваемом случае брэгговской дифракции световых пучков на ГДС в оптически неоднородном слое ФПМ, амплитуды $E_{j}^{m}(\vec {r})$ взаимодействующих волн определяются двумя системами уравнений связанных волн (УСВ) в частных производных, аналагично [12, 15]:

где $E_{j}^{m}(\vec {r})$ – амплитудные профили пучков; $\vec {N}_{{r0,1}}^{m}$ – групповые нормали; ${{\vec {E}}_{j}}(\vec {r})$ = $\vec {N}_{{r0,1}}^{m} \cdot E_{j}^{m}(\vec {r});$ $C_{j}^{m}$ – амплитудные коэффициенты связи; ${{n}_{1}}(\vec {r})$ – нормированный амплитудный профиль первой гармоники показателя преломления структуры, ${{n}_{1}}(\vec {r}) = $ $\frac{{n_{1}^{'}(\vec {r})}}{{\max \left[ {n_{1}^{'}(\vec {r})} \right]}};$ $\Delta \vec {K}$ – вектор фазовой расстройки.

Для произвольного времени записи результирующий нормированный пространственный профиль амплитуды первой гармоники ${{n}_{1}}(\vec {r}) = {{n}_{1}}(y)$ может быть неоднородным в силу условий записи [3, 14]. Таким образом, неоднородность должна быть учтена при решении дифракционной задачи. Зависимость профиля показателя преломления вдоль оси y возможно аппроксимировать функцией специального вида, аналогично [16]:

где параметры c, s, t определяют, соответственно, степень неоднородности, асимметрии, смещения и задаются путем минимизации функционала среднеквадратического отклонения аппроксимирующей функции (6) от сформированного профиля, промоделированного и представленного в [14].

В соответствии с [15, 16] амплитудные профили дифрагирующих пучков на выходе образца в ближней зоне удобно представить в апертурных координатах ${{\xi }_{0}},$ ${{\xi }_{1}}$ (рис. 1).

Уравнения преобразования координат имеют вид [13] (индекс m опущен):

где ${{\nu }_{j}} = {{N}_{{rj}}}{{y}_{0}},$ ${{\eta }_{j}} = {{N}_{{rj}}}{{z}_{0}}.$

Решения уравнений (5) в каждом слое могут быть найдены в аналитическом виде методом Римана аналогично [17, 18] в апертурных координатах (${{\xi }_{0}},$ ${{\xi }_{1}}$) и представлены в виде рекуррентных соотношений, с помощью которых последовательно можно описать процесс образования пространственных профилей $E_{0}^{{m,n}}(\xi )$ и $E_{1}^{{m,n}}(\eta )$ на выходе каждого n-го слоя, через распределения $E_{0}^{{m,n - 1}}(\xi )$ и $E_{1}^{{m,n - 1}}(\eta )$ на его входе.

где ${}_{2}{{F}_{1}}(a,b,c;z)$ – гипергеометрическая функция Гаусса; w = $\frac{{\operatorname{sh} \left[ {{{cs(1 - q)} \mathord{\left/ {\vphantom {{cs(1 - q)} 2}} \right. \kern-0em} 2}} \right]\operatorname{sh} \left[ {{{cs(1 + q)} \mathord{\left/ {\vphantom {{cs(1 + q)} 2}} \right. \kern-0em} 2}} \right]}}{{\operatorname{ch} \left[ {ct} \right]\operatorname{ch} \left[ {c(s - t)} \right]}};$ A = $ = {{\left( {csch\left[ {ct} \right]\operatorname{ch} \left[ {c(s - t)} \right]} \right)}^{{ - 1}}};$ $\alpha = b_{j}^{m};$ $b_{j}^{m}$ = $\frac{{{{d}_{n}}C_{j}^{m}}}{{\sqrt {{{\nu }_{0}}{{\nu }_{1}}} }};$ $\delta = {{d}_{n}}({{\eta }_{1}}{{\nu }_{0}} - {{{{\eta }_{0}}{{\nu }_{1}}} \mathord{\left/ {\vphantom {{{{\eta }_{0}}{{\nu }_{1}}} {2{{\nu }_{1}}}}} \right. \kern-0em} {2{{\nu }_{1}}}});$ ${{d}_{n}}$ – толщина n-го слоя; ${{\eta }_{j}} = \pm \sin {{\theta }_{{rj}}};$ ${{\nu }_{j}} = \cos {{\theta }_{{rj}}};$ ${{\theta }_{{rj}}}$ – углы между групповыми нормалями $\vec {N}_{{rj}}^{m}$ и осью y (рис. 1); $\Delta K = \left| {\Delta \vec {K}} \right| \cdot {{d}_{n}}$ – обобщенная фазовая расстройка, $C_{j}^{m}$ – коэффициенты связи; параметры c, s, t берутся для каждого слоя, согласно аппроксимирующей функции (6).

В итоге, пространственные распределения векторных световых полей в нулевом и первом дифракционных порядках на выходе n-го слоя МНГДС определяются выражениями [15, 16]:

Полученные решения полностью определяю как амплитудные, так и поляризацинные параметры дифракционных полей на выходе n-го слоя МНГДС.

Для определения дифракционного светового поля на выходе МНГДС, состоящей из N ГДС на основе ФПМ, которые разделены N – 1 промежуточными слоями, воспользуемся матричным методом описания преобразования плоских световых волн в многослойных средах.

Для этого перейдем от амплитудных распределений частотных Фурье-компонент дифрагирующих пучков (8), (9) к их угловым спектрам:

где $l = {{\xi }_{0}},$ ${{\xi }_{1}},$ а угол θ характеризует направление плосковолновых компонент $E_{j}^{{}}(\theta )$ относительно волновых нормалей.

В результате процесс преобразования частотно-угловых спектров (ЧУС) взаимодействующих световых полей 0-го и 1-го дифракционных порядок в n-м слое МНГДС толщиной d_n представляется в виде:

где введены обозначения: ${{{\mathbf{E}}}^{n}} = \left[ {\begin{array}{*{20}{c}} {E_{0}^{n}(\omega ,\theta )} \\ {E_{1}^{n}(\omega ,\theta )} \end{array}} \right],$ ${{{\mathbf{E}}}^{{'n - 1}}} = \left[ {\begin{array}{*{20}{c}} {E_{0}^{{'n - 1}}(\omega ,\theta )} \\ {E_{1}^{{'n}}(\omega ,\theta )} \end{array}} \right],$ ${{{\mathbf{T}}}^{n}} = \left[ {\begin{array}{*{20}{c}} {T_{{00}}^{n}(\omega ,\theta )}&{T_{{10}}^{n}(\omega ,\theta )} \\ {T_{{01}}^{n}(\omega ,\theta )}&{T_{{11}}^{n}(\omega ,\theta )} \end{array}} \right].$

Здесь ${{{\mathbf{T}}}^{n}}$ – матричная передаточная функция (матрица перехода) n-го слоя МНГДС; $E_{i}^{{'n - 1}}(\omega ,\theta ),$ $E_{i}^{n}(\omega ,\theta )$ – ЧУС на входе и выходе n-го слоя.

Компоненты матрицы перехода ${{{\mathbf{T}}}^{n}}$ определяются выражениями:

Следует отметить, что, в частном случае, взаимодействия плоских волн в МНГДС на основе ГДС с однородными профилями n₁(y), компоненты T_ij матрицы перехода Tⁿ, определенными выражениями (14)–(17), переходит в известные [7].

В МНГДС промежуточный слой толщиной t_n (рис. 1а) дает фазовый набег, и если считать, что показатель преломления промежуточного слоя равен показателю преломления голограммы, то матрица перехода ${{{\mathbf{A}}}^{n}}$ для такого слоя будет выглядеть следующим образом:

Перемножив матрицы перехода всех слоев, можно получить связь между входным полем E₀ и дифракционным полем E^N на выходе МНГДС толщиной D:

где ${\mathbf{T}} = {{{\mathbf{T}}}^{N}} \times {{{\mathbf{A}}}^{{N - 1}}} \times {{{\mathbf{T}}}^{{N - 1}}}$ × $...{{{\mathbf{A}}}^{n}} \times {{{\mathbf{T}}}^{n}} \times ... \times {{{\mathbf{A}}}^{1}} \times {{{\mathbf{T}}}^{1}}$ – матричная передаточная функция (матрица перехода) всей МНГДС; $D = \sum\nolimits_{n = 1}^N {{{d}_{n}}} $ + $\sum\nolimits_{n = 1}^{N - 1} {{{t}_{n}}} ,$ ${{{\mathbf{E}}}_{0}} = \left[ {\begin{array}{*{20}{c}} {{{E}_{0}}(\omega ,\theta )} \\ 0 \end{array}} \right],$ ${{E}_{0}}(\omega ,\theta )$ – ЧУС падающего на МНГДС квазиминохроматического светового пучка, определенный выражениями (1) и (12).

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Полученные передаточные функции создают математическую основу для расчета селективных свойств МНГДС, а именно: зависимости дифракционной эффективности от угла падения и центральной частоты считывающего пучка. Для этого в выражениях (14)–(17) необходимо воспользоваться зависимостями модуля вектора фазовой расстройки $\Delta K* = \left| {\Delta \vec {K}} \right|$ от угла падения и частоты считывающего пучка с учетом дисперсии показателя преломления ФПМ.

где $\Delta K{\text{*}}(\theta ) = ({D \mathord{\left/ {\vphantom {D B}} \right. \kern-0em} B})\theta ,$ $\Delta K{\text{*}}(\omega )$ = $(C - {{AD} \mathord{\left/ {\vphantom {{AD} B}} \right. \kern-0em} B})\omega ,$ а коэффициенты A, B, C, D определены в [17].

Зависимость матрицы перехода промежуточного слоя МНГДС Aⁿ от обобщенной фазовой расстройки $\Delta K = \Delta K{\text{*}}{{d}_{n}}$ получим на основании выражения (18) и представим в виде:

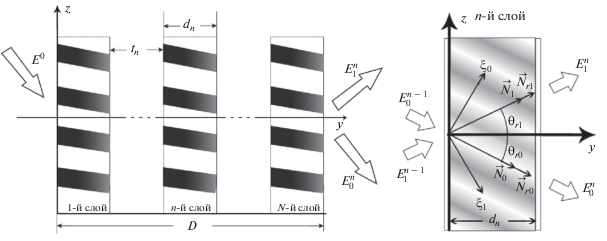
На основе представленных аналитических решений исследованы селективные свойства двуслойной структуры с однородным профилем показателя преломления c различными толщинами промежуточного слоя t_n и слоя дифракционной структуры содержащей ФПМ d_n (рис. 2). Для этого в выражении (21) отношение t_n/d_n выразим через параметр $q = {{{{t}_{n}}} \mathord{\left/ {\vphantom {{{{t}_{n}}} {{{d}_{n}}}}} \right. \kern-0em} {{{d}_{n}}}}.$

Из рис. 2а видно, что при небольшой толщине промежуточного слоя, когда ($q \to 0$) вид контура селективности всей структуры близок к виду характеристики одиночной голографической структуры. А при увеличении этого параметра вследствие интерференционных эффектов образуются дополнительные локальные максимумы и минимумы интенсивности света, при этом общая величина дифракционной эффективности сохраняется, а огибающая совпадает с контуром селективности при $q = 0.$ Количество дополнительно возникаемых максимумов, выше уровня 0.5 максимальной дифракционной эффективности, растет линейно с увеличением отношения толщины промежуточного слоя к толщине слоя с дифракционной структурой, а их ширина и расстояние между ними экспоненциально убывают (рис. 2б).

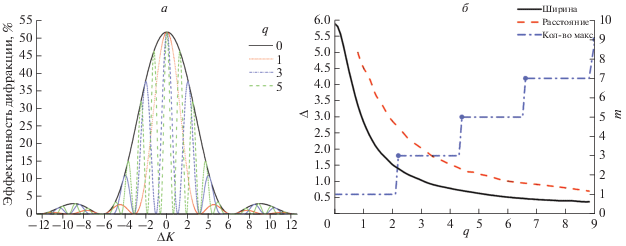
На основе численного моделирования, рассчитаны селективные свойства трехслойной МНГДС, пространственные профили показателей преломления которой получены в результате решения задачи формирования [14]. Рассмотрены случаи с сильно (рис. 3б) и слабо выраженной степенью неоднородности профиля показателя преломления на каждом слое (рис. 3г).

При моделировании, ошибка аппроксимации нормированных пространственных профилей показателей преломления, функцией (6) не превышала 3%. Толщина промежуточного слоя t_n = 200 мкм, толщина одного слоя ГДС ${{d}_{n}} = 85$ мкм.

Результаты моделирования, представленные на рис. 3 показали, что огибающая контура селективности всей структуры совпадает с контуром селективности одиночной голографической структуры, формируемой на первом слое. Количество и ширина локальных максимумов определяются толщиной промежуточных слоев. Амплитуды локальных максимумов изменяются в больших пределах, и зависят от пространственного распределения показателей преломления каждого слоя. Ширина и вид огибающей контура селективности всей многослойной структуры зависит от пространственного распределения показателей преломления на первом слое.

В процессе формирования МНГДС, может происходить искажение пространственной структуры голограмм (изменение периода и углов наклона решеток), вследствие различной усадки материала на каждом слое, связанной с изменением интенсивности (затуханием) формирующих пучков при прохождении от слоя к слою [5, 19, 20].

Для учета усадки материала введем аддитивную добавку $\Delta K_{{{\text{усад}}}}^{n},$ которая является параметром, характеризующим искажение пространственной структуры голографической решетки на каждом слое МНГДС. Тогда зависимость модуля вектора фазовой расстройки $\Delta K{\text{*}}$ от угла падения и частоты считывающего пучка с учетом дисперсии показателя преломления ФПМ и усадки материала запишем в виде:

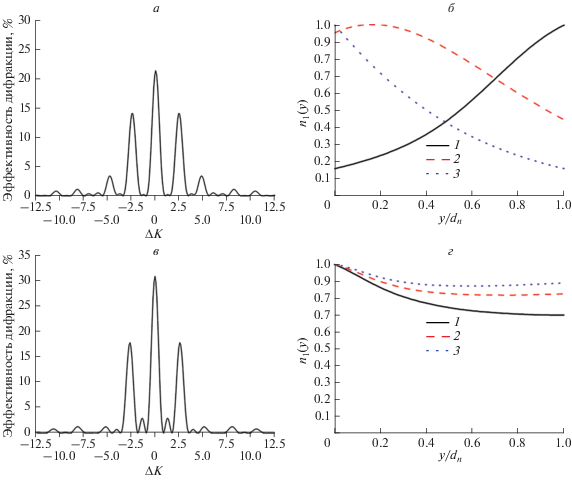
При помощи численного моделирования исследованы селективные свойства двуслойной структуры, с однородным и спадающим профилем показателя преломления на каждом слое МНГДС (рис. 4). Толщина промежуточного слоя t_n = 175 мкм, толщина одного слоя ГДС ${{d}_{n}} = 55$ мкм. При моделировании учтена различная степень усадки материала для каждого слоя, $\Delta K_{{{\text{усад}}}}^{1} = - 4,$ $\Delta K_{{{\text{усад}}}}^{2} = - 2.$

Из результатов численного моделирования селективных свойств МНГДС, учитывающего искажение пространственной структуры голографической дифракционной решетки вследствие усадки материала при формировании, можно наблюдать смещение характеристики селективных свойств МНГДС от слоя к слою, а также асимметрию боковых лепестков.

ЗАКЛЮЧЕНИЕ

Таким образом, в работе представлена самосогласованная аналитическая модель взаимодействия квазимонохроматических световых пучков с МНГДС которая учитывает пространственные неоднородности амплитудного профиля гармоник показателя преломления, возникающих в процессе голографического формирования решеток в фотополимерном материале. Представленные аналитические решения описывают эволюцию пространственных профилей световых пучков и их частотно-угловых спектров при дифракции на МНГДС. Выражения (14)–(17) создают математическую основу для расчета селективных свойств МНГДС, а также для описания преобразование светового излучения со сложным ЧУС при его взаимодействии с МНГДС на основе ФПМ.

Работа выполнена при поддержке Минобрнауки Российской Федерации в рамках государственного задания (FEWM-2020-0038/30).