Известия РАН. Серия физическая, 2021, T. 85, № 11, стр. 1546-1549

Отношение вектора Пойнтинга и вектора групповой скорости электромагнитных волн в неограниченной ферромагнитной среде

Э. Г. Локк^1, *, А. В. Луговской¹, С. В. Герус¹, А. Ю. Анненков¹

¹ Федеральное государственное бюджетное учреждение науки Институт радиотехники и электроники имени В.А. Котельникова Российской академии наук, Фрязинский филиал
Фрязино, Россия

^* E-mail: edwin@ms.ire.rssi.ru

Поступила в редакцию 21.06.2021
После доработки 05.07.2021
Принята к публикации 28.07.2021

DOI: 10.31857/S036767652111020X

Полный текст (PDF)

Аннотация

Рассчитаны ориентация вектора Пойнтинга и ориентация вектора групповой скорости в зависимости от ориентации волнового вектора для различных типов электромагнитных волн, распространяющихся в безграничной ферромагнитной среде. Установлено, что вектор Пойнтинга и вектор групповой скорости всегда сонаправлены для всех типов волн в данной среде.

В девятнадцатом веке в физику были введены понятия “вектор Пойнтинга” и “вектор групповой скорости” для описания распространения волн в изотропной среде. Впервые представление о групповой скорости, которая отличается от фазовой скорости волны, использовали Гамильтон, Стокс и Рэлей, а идею о потоке энергии ввели в физику позже Умов и Пойнтинг. В дальнейшем при использовании вектора групповой скорости $\vec {U}$ и вектора Пойнтинга $\vec {P}$ для описания волн в анизотропных средах было установлено, что в отсутствие поглощения у плоских волн в анизотропной среде скорость переноса энергии равна групповой скорости [1] и что в немагнитной среде, описываемой симметричным тензором диэлектрической проницаемости, векторы $\vec {P}$ и $\vec {U}$ нормальны поверхности волновых векторов [2]. В дальнейшем аналогичные результаты были получены и для электромагнитных волн (ЭМВ) в гипотетической неограниченной бигиротропной среде, которую характеризуют эрмитовые тензоры диэлектрической и магнитной проницаемостей [3].

Поскольку в работах [2, 3] фактически доказано, что векторы $\vec {P}$ и $\vec {U}$ нормальны одной и той же поверхности, то возникает вопрос: всегда ли эти векторы направлены одинаково или же существуют среды (условия), когда эти векторы могут быть направлены противоположно? Очевидно, что для сравнения ориентаций векторов $\vec {P}$ и $\vec {U}$ для случая произвольного направления распространения волны необходимо получить для этих векторов аналитические выражения в какой-нибудь анизотропной среде, причем при выводе данных выражений не следует использовать приближенные методы. Опираясь на описание ЭМВ в бигиротропной среде [4–8], ниже рассчитаны ориентации векторов $\vec {P}$ и $\vec {U}$ для ЭМВ в неограниченной ферромагнитной среде, являющейся частным случаем бигиротропной среды.

Рассмотрим неограниченную ферромагнитную среду, которая находится в постоянном однородном магнитном поле ${{\vec {H}}_{{C0}}},$ направленном вдоль оси z. Такая среда характеризуется скалярной диэлектрической проницаемостью ε и эрмитовым тензором магнитной проницаемости ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }}$

(1)

${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {\mu } }} = \left| {\begin{array}{*{20}{c}} \mu &{i\nu }&0 \\ { - i\nu }&\mu &0 \\ 0&0&{{{\mu }_{{zz}}}} \end{array}} \right|,$

недиагональные компоненты которого μ и ν определяются выражениями [5]

(2)

$\mu = 1 + \frac{{{{\omega }_{M}}{{\omega }_{H}}}}{{\omega _{H}^{2} - {{\omega }^{2}}}} = \frac{{\omega _{ \bot }^{2} - {{\omega }^{2}}}}{{\omega _{H}^{2} - {{\omega }^{2}}}},$

(3)

$\nu = \frac{{{{\omega }_{M}}\omega }}{{\omega _{H}^{2} - {{\omega }^{2}}}},$

где γ – гиромагнитная постоянная, $4\pi {{M}_{{c0}}}$ – намагниченность насыщения феррита, ${{\omega }_{H}} = \gamma {{H}_{{c0}}},$ ${{\omega }_{M}} = \gamma 4\pi {{M}_{{c0}}},$ $\omega _{ \bot }^{2} = {{\omega }_{H}}({{\omega }_{H}} + {{\omega }_{M}}).$

Электромагнитная волна с частотой ω, распространяющаяся в данной среде и изменяющаяся во времени по закону $ \sim {\kern 1pt} \exp (i\omega t),$ должна удовлетворять уравнениям Максвелла. Будем искать решение уравнений Максвелла в виде однородной плоской волны с волновым вектором $\vec {k},$ считая, что комплексные амплитуды векторов напряженностей высокочастотных электрического и магнитного полей $\vec {E}$ и $\vec {H}$ (а также их компоненты E_x, E_y, E_z, H_x, H_y и H_z) изменяются в пространстве по гармоническому закону

(4)

$\begin{gathered} \vec {E} = {{{\vec {E}}}_{0}}\exp ( - i\vec {k}\vec {r})\,\,\,{\text{или}} \\ {{E}_{{x,y,z}}} = {{E}_{{x0,y0,z0}}}\exp ( - i{{k}_{x}}x - i{{k}_{y}}y - i{{k}_{z}}z), \\ \end{gathered} $

(5)

$\begin{gathered} \vec {H} = {{{\vec {H}}}_{0}}\exp ( - i\vec {k}\vec {r})\,\,\,{\text{или}} \\ {{H}_{{x,y,z}}} = {{H}_{{x0,y0,z0}}}\exp ( - i{{k}_{x}}x - i{{k}_{y}}y - i{{k}_{z}}z). \\ \end{gathered} $

Здесь использованы декартова $\{ x;~y;~z\} $ и сферическая $\{ r;~\varphi ;~\theta \} $ системы координат, базисы которых связаны соотношениями $x = r\sin \theta \cos \varphi ,$ $y = r\sin \theta \sin \varphi ,$ $z = r\cos \theta ,$ причем модуль вектора $\vec {k}$ и его компоненты также связаны соотношениями ${{k}_{x}} = k\sin \theta \cos \varphi ,$ ${{k}_{y}} = k\sin \theta \sin \varphi ,$ ${{k}_{z}} = k\cos \theta ,$ ${{k}^{2}} = k_{x}^{2} + k_{y}^{2} + k_{z}^{2}.$

Решая уравнения Максвелла по аналогии с работами [4, 6–8], найдем дисперсионное уравнение для ЭМВ в безграничной ферритовой среде [8]

(6)

$F(\omega ,\vec {k}) = {{F}_{{{\nu }}}}{{F}_{g}} - {{\mu }_{{zz}}}\varepsilon F_{{{v}g}}^{2} = 0.$

Здесь безразмерные величины ${{F}_{{{\nu }}}},$ ${{F}_{g}}$ и ${{F}_{{{{\nu }}g}}}$ определяют выражения

(7)

${{F}_{{{\nu }}}} = {{{{k}^{2}}} \mathord{\left/ {\vphantom {{{{k}^{2}}} {k_{0}^{2}}}} \right. \kern-0em} {k_{0}^{2}}} - \varepsilon {{\mu }_{ \bot }},$

(8)

${{F}_{g}} = \frac{{{{k}^{2}}}}{{k_{0}^{2}}}\left( {{{{\sin }}^{2}}\theta + \frac{{{{\mu }_{{zz}}}}}{\mu }{{{\cos }}^{2}}\theta } \right) - {{\mu }_{{zz}}}\varepsilon ,$

(9)

${{F}_{{{{\nu }}g}}} = \frac{k}{{{{k}_{0}}}}\frac{\nu }{\mu }\cos \theta ,$

где c – скорость света в вакууме, а k₀ = ω/c.

В соответствии с [8] все электрические и магнитные компоненты ЭМВ в данной среде можно записать через амплитуду компоненты E_z0

(10)

$\begin{gathered} {{H}_{x}} = \frac{{{{E}_{{z0}}}}}{{{{k}^{2}}{{{\sin }}^{2}}\theta }}\left( {i\varepsilon \frac{\nu }{\mu }{{k}_{x}}{{k}_{0}} - i\frac{{{{F}_{\nu }}}}{{\mu {{F}_{{\nu g}}}}}{{k}_{x}}{{k}_{z}} + \varepsilon {{k}_{y}}{{k}_{0}}} \right) \times \\ \times \,\,\exp ( - i{{k}_{x}}x - i{{k}_{y}}y - i{{k}_{z}}z), \\ \end{gathered} $

(11)

$\begin{gathered} {{H}_{y}} = \frac{{{{E}_{{z0}}}}}{{{{k}^{2}}{{{\sin }}^{2}}\theta }}\left( {i\varepsilon \frac{\nu }{\mu }{{k}_{y}}{{k}_{0}} - i\frac{{{{F}_{\nu }}}}{{\mu {{F}_{{\nu g}}}}}{{k}_{y}}{{k}_{z}} - \varepsilon {{k}_{x}}{{k}_{0}}} \right) \times \\ \times \,\,\exp ( - i{{k}_{x}}x - i{{k}_{y}}y - i{{k}_{z}}z), \\ \end{gathered} $

(12)

${{H}_{z}} = i{{E}_{{z0}}}\frac{{{{F}_{{{\nu }}}}}}{{{{\mu }_{{zz}}}{{F}_{{{{\nu }}g}}}}}\exp ( - i{{k}_{x}}x - i{{k}_{y}}y - i{{k}_{z}}z),$

(13)

$\begin{gathered} {{E}_{x}} = - \frac{{{{E}_{{z0}}}}}{{{{k}^{2}}{{{\sin }}^{2}}\theta }}\left( {{{k}_{x}}{{k}_{z}} + {{i{{F}_{{{\nu }}}}{{k}_{y}}{{k}_{0}}} \mathord{\left/ {\vphantom {{i{{F}_{{{\nu }}}}{{k}_{y}}{{k}_{0}}} {{{F}_{{{{\nu }}g}}}}}} \right. \kern-0em} {{{F}_{{{{\nu }}g}}}}}} \right) \times \\ \times \,\,\exp ( - i{{k}_{x}}x - i{{k}_{y}}y - i{{k}_{z}}z). \\ \end{gathered} $

(14)

$\begin{gathered} {{E}_{y}} = \frac{{{{E}_{{z0}}}}}{{{{k}^{2}}{{{\sin }}^{2}}\theta }}\left( {{{i{{F}_{{{\nu }}}}{{k}_{x}}{{k}_{0}}} \mathord{\left/ {\vphantom {{i{{F}_{{{\nu }}}}{{k}_{x}}{{k}_{0}}} {{{F}_{{{{\nu }}g}}}}}} \right. \kern-0em} {{{F}_{{{{\nu }}g}}}}} - {{k}_{y}}{{k}_{z}}} \right) \times \\ \times \,\,\exp ( - i{{k}_{x}}x - i{{k}_{y}}y - i{{k}_{z}}z). \\ \end{gathered} $

Вектор Пойнтинга $\vec {P},$ как известно, описывается формулой

(15)

$\vec {P} = \frac{c}{{8\pi }}\operatorname{Re} \left[ {\vec {E}\vec {H}{\text{*}}} \right],$

а выражения для его компонент будут иметь вид:

(16)

${{P}_{x}} = {{k}_{x}}\frac{{\varepsilon \omega E_{{z0}}^{2}}}{{8\pi {{F}_{g}}{{k}^{2}}{{{\sin }}^{2}}\theta }}\left( {{{F}_{{{\nu }}}} + {{F}_{g}}} \right),$

(17)

${{P}_{y}} = {{k}_{y}}\frac{{\varepsilon \omega E_{{z0}}^{2}}}{{8\pi {{F}_{g}}{{k}^{2}}{{{\sin }}^{2}}\theta }}\left( {{{F}_{{{\nu }}}} + {{F}_{g}}} \right),$

(18)

${{P}_{z}} = {{k}_{z}}\frac{{\varepsilon \omega E_{{z0}}^{2}}}{{8\pi {{F}_{g}}{{k}^{2}}{{{\sin }}^{2}}\theta }}\left[ {\frac{{{{\mu }_{{zz}}}}}{\mu }{{F}_{{{\nu }}}} + {{F}_{g}} - \varepsilon {{\mu }_{{zz}}}{{{\left( {\frac{\nu }{\mu }} \right)}}^{2}}} \right].$

Прежде, чем получить выражения для вектора групповой скорости $\overrightarrow U $ и его компонент, отметим, что в анизотропных средах использовать понятие “групповая скорость” в соответствии с [9, 10] можно лишь на некотором конечном расстоянии, на котором форма сигнала, модулирующего синусоидальную волну, практически не искажается, причем величина этого расстояния зависит от дисперсионных характеристик среды. Очевидно, что если ограничиться рассмотрением случаев, когда модулируемая волна распространяется на бесконечно малое расстояние, то понятие групповой скорости можно использовать практически в любой среде. При сформулированных условиях выражение для вектора $\vec {U}$ определяется выражением [8, 9]

(19)

$\vec {U} = \frac{{d\omega }}{{d\vec {k}}} = gra{{d}_{{\vec {k}}}}\omega = \frac{{\partial \omega }}{{\partial {{k}_{x}}}}{{\vec {x}}_{{\text{0}}}} + \frac{{\partial \omega }}{{\partial {{k}_{y}}}}{{\vec {y}}_{{\text{0}}}} + \frac{{\partial \omega }}{{\partial {{k}_{z}}}}{{\vec {z}}_{{\text{0}}}}.$

Отметим, что в анизотропных средах зависимость $\omega (\vec {k})$ удается вывести в явном виде очень редко, тогда как дисперсионное уравнение волны $F(\omega ,\vec {k}) = 0$ можно получить гораздо чаще. Поэтому, воспользовавшись правилом дифференцирования неявной функции, запишем выражение (19) в виде

(20)

$\begin{gathered} \vec {U} = - \frac{{{{\partial F} \mathord{\left/ {\vphantom {{\partial F} {d\vec {k}}}} \right. \kern-0em} {d\vec {k}}}}}{{{{\partial F} \mathord{\left/ {\vphantom {{\partial F} {\partial \omega }}} \right. \kern-0em} {\partial \omega }}}} = - {{\left( {\frac{{\partial F}}{{\partial \omega }}} \right)}^{{ - 1}}}gra{{d}_{{\vec {k}}}}F = \\ = - {{\left( {\frac{{\partial F}}{{\partial \omega }}} \right)}^{{ - 1}}}\left( {\frac{{\partial F}}{{\partial {{k}_{x}}}}{{{\vec {x}}}_{{\text{0}}}} + \frac{{\partial F}}{{\partial {{k}_{y}}}}{{{\vec {y}}}_{{\text{0}}}} + \frac{{\partial F}}{{\partial {{k}_{z}}}}{{{\vec {z}}}_{{\text{0}}}}} \right). \\ \end{gathered} $

Выражения для компонент вектора групповой скорости ЭМВ, полученные на основе соотношения (20) для ферромагнитной среды, будут иметь вид

(21)

${{U}_{x}} = - 2\frac{{{{k}_{x}}}}{{k_{0}^{2}}}{{\left( {\frac{{\partial F}}{{\partial \omega }}} \right)}^{{ - 1}}}\left( {{{F}_{{{\nu }}}} + {{F}_{g}}} \right),$

(22)

${{U}_{y}} = - 2\frac{{{{k}_{y}}}}{{k_{0}^{2}}}{{\left( {\frac{{\partial F}}{{\partial \omega }}} \right)}^{{ - 1}}}\left( {{{F}_{{{\nu }}}} + {{F}_{g}}} \right),$

(23)

${{U}_{z}} = - 2\frac{{{{k}_{z}}}}{{k_{0}^{2}}}{{\left( {\frac{{\partial F}}{{\partial \omega }}} \right)}^{{ - 1}}}\left[ {\frac{{{{\mu }_{{zz}}}}}{\mu }{{F}_{{{\nu }}}} + {{F}_{g}} - \varepsilon {{\mu }_{{zz}}}{{{\left( {\frac{\nu }{\mu }} \right)}}^{2}}} \right],$

где производная ∂F/∂ω может быть найдена из дисперсионного уравнения (6)

(24)

$\begin{gathered} \frac{{\partial F}}{{\partial \omega }} = - \left( {2\frac{{k_{{{\varphi }}}^{2}}}{{\omega k_{0}^{2}}} + 2\frac{{k_{z}^{2}}}{{\omega k_{0}^{2}}} + \varepsilon \frac{{\partial {{\mu }_{ \bot }}}}{{\partial \omega }}} \right){{F}_{g}} - \\ - \,\,\left( {2\frac{{k_{{{\varphi }}}^{2}}}{{\omega k_{0}^{2}}} + 2\frac{{{{\mu }_{{zz}}}}}{\mu }\frac{{k_{z}^{2}}}{{\omega k_{0}^{2}}} + \frac{{{{\mu }_{{zz}}}}}{{{{\mu }^{2}}}}\frac{{k_{z}^{2}}}{{k_{0}^{2}}}\frac{{\partial \mu }}{{\partial \omega }}} \right){{F}_{{{\nu }}}} - \\ - \,\,2\varepsilon {{\mu }_{{zz}}}\frac{\nu }{\mu }\frac{{k_{z}^{2}}}{{k_{0}^{2}}}\left[ {\frac{{\partial \left( {\nu {\text{/}}\mu } \right)}}{{\partial \omega }} - \frac{\nu }{{\mu \omega }}} \right]. \\ \end{gathered} $

Здесь ${{\mu }_{ \bot }} = {{({{\mu }^{2}} - {{\nu }^{2}})} \mathord{\left/ {\vphantom {{({{\mu }^{2}} - {{\nu }^{2}})} \nu }} \right. \kern-0em} \nu },$ а производные величин μ, ${{\mu }_{ \bot }}$ и ν/μ несложно найти из выражений (2) и (3).

Как следует из [6], все изочастотные поверхности ЭМВ в неограниченной ферромагнитной среде образованы путем вращения соответствующих изочастотных зависимостей вокруг оси z (см. рис. 1 и 2 в [6]). Таким образом, можно рассмотреть ориентации векторов $\vec {P}$ и $\vec {U}$ только для точек изочастотной зависимости, являющейся сечением этой поверхности плоскостью, проходящей через ось z (в данном случае – плоскостью xz). Поскольку в исследуемой среде векторы $\vec {k},$ $\vec {U}$ и $\vec {P}$ не всегда могут быть ориентированы вдоль оси z, то их ориентации удобнее отсчитывать от оси x. Поэтому введем угол θ', определяющий ориентацию вектора $\vec {k}$ относительно оси x и связанный с введенным ранее углом θ соотношением θ' = θ + 90°, и, используя выражения (21)–(23), найдем углы ψ_U и ψ_P, определяющие ориентации векторов $\vec {U}$ и $\vec {P}$ относительно оси x

(25)

${{\psi }_{U}} = \operatorname{arctg} ({{{{U}_{z}}} \mathord{\left/ {\vphantom {{{{U}_{z}}} {{{U}_{x}}}}} \right. \kern-0em} {{{U}_{x}}}}),$

(26)

${{\psi }_{P}} = \operatorname{arctg} ({{{{P}_{z}}} \mathord{\left/ {\vphantom {{{{P}_{z}}} {{{P}_{x}}}}} \right. \kern-0em} {{{P}_{x}}}}).$

Рис. 1.

Изочастотные зависимости (а) и ориентации ψ_U и ψ_P вектора групповой скорости и вектора Пойнтинга (б) в зависимости от ориентации θ' волнового вектора для нерезонансных ЭМВ с частотами 0.3, 1.8, 6 и 20 ГГц (кривые 1–4).

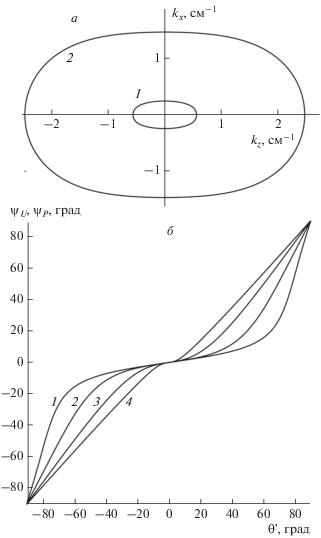
Рис. 2.

Изочастотные зависимости для k_x > 0 (а) и ориентации ψ_U и ψ_P вектора групповой скорости и вектора Пойнтинга (б) в зависимости от ориентации θ' волнового вектора для спиновых волн с частотами 0.3, 0.55, 0.8, 1.3, 1.77 и 2.05 ГГц (кривые 1–6). Изображены также произвольный волновой вектор $\vec {k},$ соответствующий ему вектор групповой скорости $\vec {U}$ и углы $\theta _{k}^{'}$ и ψ_U, определяющие ориентации этих векторов.

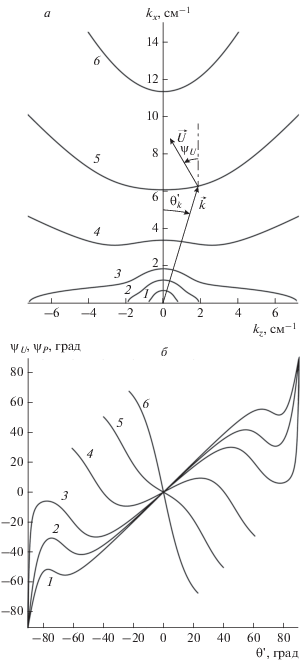
Зависимости ψ_U(θ') и ψ_P(θ') для нерезонансной и спиновой волн в ферромагнитной среде [6], а также изочастотные зависимости этих волн представлены, соответственно, на рис. 1 и 2 . При расчетах использованы следующие параметры среды: H_c0 = 300 Э, ε = 15 и 4πM_c0= 1750 Гс. Следует отметить, что при вычислении углов ψ_U и ψ_P по формулам (25) и (26) для противоположно направленных векторов будут получены одинаковые значения углов, поэтому рассчитанные значения этих углов дополнительно проверялись на основе сравнения знаков одинаковых проекций векторов $\vec {U}$ и $\vec {P}$ (U_x и P_x, а также U_z и P_z). В итоге, найдено, что в ферромагнитной среде ориентации ψ_U и ψ_P векторов $\vec {U}$ и $\vec {P}$ для всех типов ЭМВ (включая пострезонансные ЭМВ [6], для которых зависимости ψ_U(θ') и ψ_P(θ') на рисунках не представлены) всегда совпадают.

Отметим, что одинаковая ориентация векторов $\vec {U}$ и $\vec {P},$ характерная для всех типов ЭМВ в ферромагнитной среде, по-видимому, обусловлена определенными причинно-следственными условиями, в частности, положительными значениями производных в выражении (24) (подробнее об этом см. §80 и §84 в [2]). В то же время, вопрос о взаимной ориентации векторов $\vec {U}$ и $\vec {P}$ в других, более сложных средах и, в частности, в средах с потерями, остается пока открытым.

Работа выполнена за счет бюджетного финансирования в рамках государственного задания по теме № 0030-2019-0014.

Список литературы

Агранович В.М., Гинзбург В.Л. Кристаллооптика с учетом пространственной дисперсии и теория экситонов. М.: Наука, 1979.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, гл. ред. физ.-мат. лит., 1982. 620 с.
Локк Э.Г., Герус С.В., Анненков А.Ю. // Изв. РАН. Сер. физ. 2020. Т. 84. № 5. С. 714; Gerus S.V., Lock E.H., Annenkov A.Yu. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 5. P. 587.
Гуревич А.Г. Ферриты на сверхвысоких частотах. Москва: Гос. изд. физ.-мат. лит., 1960. 407 с.
Гуревич А.Г., Мелков Г.А. Магнитные колебания и волны. М.: Наука, 1994. 464 с.
Локк Э.Г. // Радиотехн. и электрон. 2017. Т. 62. № 3. С. 259; Lokk E.G. // J. Commun. Technol. Electron. 2017. V. 62. No. 3. P. 251.
Локк Э.Г., Герус С.В., Анненков А.Ю. // Тр. XXVII Межд. конф. “Электромагнитное поле и материалы (фундаментальные физические исследования)”. (Москва, 2018). С. 115.
Локк Э.Г., Луговской А.В., Герус С.В. // Радиотехн. электрон. 2021. Т. 66. № 7. С. 662; Loсk E.H., Lugovskoi A.V., Gerus S.V. // J. Commun. Technol. Electron. 2021. V. 66. № 7. P. 834.
Мандельштам Л.И. Лекции по оптике, теории относительности и квантовой механике. М.: Наука, 1972. 440 с.
Локк Э.Г. // Изв. РАН. Сер. физ. 2018. Т. 82. № 8. С. 1080; Loсk E.H. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. No. 8. P. 978.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал