Известия РАН. Серия физическая, 2021, T. 85, № 11, стр. 1554-1558

Исследование области устойчивой работы элементов магниторезистивных запоминающих элементов

О. П. Поляков^1, *, С. И. Касаткин², В. В. Амеличев³, П. А. Поляков¹

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

² Федеральное государственное бюджетное учреждение науки Институт проблем управления имени В.А. Трапезникова Российской академии наук
Москва, Россия

³ Федеральное государственное бюджетное научное учреждение “Научно-производственный комплекс "Технологический центр”
Москва, Россия

^* E-mail: o_polyakov@physics.msu.ru

Поступила в редакцию 21.06.2021
После доработки 05.07.2021
Принята к публикации 28.07.2021

DOI: 10.31857/S0367676521110302

Полный текст (PDF)

Аннотация

Исследована область устойчивой работы элементов магниторезистивных запоминающих элементов с учетом поля неоднородности фиксирующего нано-магнитного слоя. В приближении однородного намагничивания вычислен коэффициент магнитостатического взаимодействия чувствительного и фиксированного слоев. Найдены оптимальные значения импульса магнитного поля, переключающие битовые состояния.

ВВЕДЕНИЕ

Ключевым элементом магниторезистивной (МР) оперативной памяти (MRAM) является спин-туннельный (СТМР) запоминающий элемент (ЗЭ). СТМР переход состоит из проводящего свободного магнитного слоя (СМС), диэлектрического барьерного слоя (ДБС), проводящего фиксированного магнитного слоя (ФМС) [1, 2]. Вектор намагниченности фиксированного слоя ${{\vec {M}}_{1}},$ направленный вдоль оси анизотропии, обладает высоким полем перемагничивания и не изменяет своего направления при изменении ориентации ${{\vec {M}}_{2}}$ в СМС. Два устойчивых состояния вектора намагниченности в СМС кодируют бит информации, которые регистрируются посредством изменения магнитосопротивления СТМР перехода. Для устойчивой работы СТМР ЗЭ MRAM необходимо найти оптимальные физические параметры и значения компонент вектора импульса магнитного поля, при которых происходит устойчивая запись бита информации. Исследования в этом направлении для различных модификаций MRAM активно ведутся на протяжении более 20 лет [1, 2]. Так в работе [3] проведено теоретическое исследование области магнитных полей, при которых происходит переключение направления вектора $\vec {M}$ в СМС из одного устойчивого состояния в другое. Магнитные полоски моделировались сильно сплюснутыми одинаковыми эллипсоидами с однородным распределением намагниченности. Плотность магнитостатической энергии взаимодействие поло-сок полагалась равной

(1)

${{w}_{c}} = - ({{\vec {M}}_{2}}{{\vec {H}}_{{m1}}}),$

где ${{\vec {M}}_{2}}$ – вектор намагниченности второй полоски, ${{\vec {H}}_{{m1}}}$ – магнитное поле создаваемое первой полоской в области второй полоски, которое считалось однородным и совпадающим с размагничивающим полем внутри эллипсоида, то есть внутри первой полоски. Этим же автором в [4] проведено развитие теории на случай различных по толщине полосок (эллипсоидов). В работе [5] сделана попытка учесть отличие магнитного поля вне полоски ФМС от поля размагничивания внутри этой полоски, предполагая, что это поле пропорционально полю размагничивания, вводя некоторый уменьшающий постоянный коэффициент $r$= 0.8, т.е. полагая

(2)

${{\vec {H}}_{{m2}}} = r{{\vec {H}}_{{m1}}}.$

В данной работе проведено исследование области устойчивой работы СТМР ЗЭ по аналогии с работами [3–5], используя точное выражение для магнитного поля однородно намагниченного эллипсоида.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ

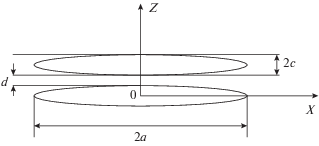
Следуя работам [3–5], рассмотрим два ферромагнитных слоя в виде сильно сплюснутых вдоль координатной оси Z однородно намагниченных эллипсоида (рис. 1). Пусть полуоси эллипсоидов $a > b > c$ ориентированы вдоль декартовых осей координатных X, Y, Z. На рис. 1 изображено сечение этих эллипсоидов координатной плоскостью X0Z.

Рис. 1.

Сечение эллипсоидальных магнитных полосок ячейки MRAM координатной плоскостью X0Z.

Пусть нижняя эллипсоидальная магнитная полоска намагничена вдоль координатной оси X и является магнитожесткой с бесконечно большой коэрцитивной силой (ФМС ЗЭ), т.е. вектор намагниченности этой полоски ${{\vec {M}}_{1}}$ всегда ориентирован вдоль координатной оси X. Верхняя эллипсоидальная магнитная полоска (СМС ЗЭ) имеет кристаллическую анизотропию и анизотропию формы вдоль координатной оси X и, соответственно, имеет две устойчивые ориентации вектора намагниченности ${{\vec {M}}_{2}}$ этого слоя – вдоль и против координатной оси X. Геометрические размеры слоев изображены на рис. 1, где $d$ – расстояние между слоями, то есть толщина ДБС СТМР перехода. Толщины с ферромагнитных эллипсоидов (пленок) в общем случае могут не совпадать.

Магнитостатическое поле вне эллипсоида будет неоднородным и только приближенно может считаться приблизительно равным однородному размагничивающему полю внутри ФМС, что предполагалось в работах [3–5]. Для точного расчета этого поле воспользуемся известным выражениям для магнитостатического потенциала однородно намагниченного эллипсоида вне эллипсоида [6]

(3)

$\varphi (x,y,z) = 4\pi \frac{{abc}}{2}\int\limits_{{{\xi }}(x,y,z)}^\infty {\frac{{dt}}{{({{a}^{2}} + t)R(t)}}} {{M}_{{1x}}}x,$

где

(4)

$R(t) = \sqrt {({{a}^{2}} + t)({{b}^{2}} + t)({{c}^{2}} + t)} .$

Здесь учтено, что вектор намагниченности ${{\vec {M}}_{1}}$ направлен вдоль оси X и имеет только одну ненулевую компоненту

(5)

${{M}_{{1x}}} = \left| {{{{\vec {M}}}_{1}}} \right| = M.$

Величина $\xi $ является эллипсоидальной координатой, зависимость которой от декартовых координат $\xi (x,y,z)$ определяется решением уравнения [7]

(6)

$\frac{{{{x}^{2}}}}{{{{a}^{2}} + \xi }} + \frac{{{{y}^{2}}}}{{{{b}^{2}} + \xi }} + \frac{{{{z}^{2}}}}{{{{c}^{2}} + \xi }} = 1.$

Проекция вектора напряженности ${{H}_{x}}$ вне эллипсоида, согласно выражению (3), будет равна

(7)

$\begin{gathered} {{H}_{x}} = - \frac{{\partial \varphi }}{{\partial x}} = 4\pi \frac{{abc}}{2} \times \\ \times \,\,\left( {\frac{x}{{({{a}^{2}} + \xi )R(\xi )}}\frac{{\partial \xi (x,y,z)}}{{\partial x}} - \int\limits_{\xi (x,y,z)}^\infty {\frac{{dt}}{{({{a}^{2}} + t)R(t)}}} } \right){{M}_{{1x}}}. \\ \end{gathered} $

Выражение (7) выражается через неполные эллиптические интегралы первого и второго рода. Зависимость $\xi (x,y,z)$ значительно упрощается при $y$ = 0 и, согласно (6), будет определяться выражением

(8)

$\begin{gathered} \xi (x,y,z) = \\ = \sqrt {{{{\left( {\frac{{{{a}^{2}} + {{c}^{2}} - {{x}^{2}} - {{z}^{2}}}}{2}} \right)}}^{2}} - {{a}^{2}}{{c}^{2}} + {{x}^{2}}{{c}^{2}} + {{z}^{2}}{{a}^{2}}} - \\ - \,\,\left( {\frac{{{{a}^{2}} + {{c}^{2}} - {{x}^{2}} - {{z}^{2}}}}{2}} \right). \\ \end{gathered} $

С помощью формул (7) и (8) была рассчитана зависимость проекции напряженности ${{H}_{x}}$ от координаты x вдоль больших полуосей верхнего эллипсоида, когда $z = 2c + d$ (рис. 1), для магнитных полосок из FeNiCo с намагниченностью насыщения $M = 1050$ Гс, в двух случаях: a = 3 мкм, b = 1 мкм, c = 5 нм, d = 3 нм и a = 0.3 мкм, b = = 0.1 мкм, c = 5 нм, d = 3 нм. Графики этой зависимости представлены на рис. 2.

Рис. 2.

Зависимость проекции напряженности H_x от координаты x вдоль больших полуосей верхнего эллипсоида при c = 5 нм, d = 3 нм в случаях: a = 3 мкм, b = 1 мкм (а) и a = 0.3 мкм, b = 0.1 мкм (б).

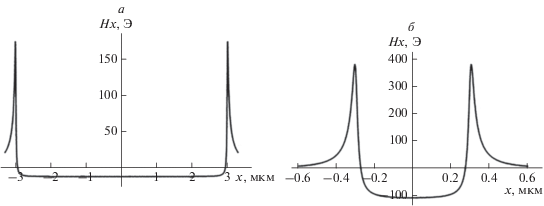
Из рис. 2a следует, что в первом случае проекция напряженности ${{H}_{x}}$ вдоль большей оси симметрии эллипсоида в основном практически постоянна и близка к значению в центре эллипсоида H_x(0) = –11.57 Э. Значение размагничиваю-щего поля внутри нижней эллипсоидальной пластинки ${{H}_{{m1}}}_{x}$= –11.63 Э. Следовательно, на большей части верхнего эллипсоида СМС магнитное поле, порожденное нижней полоской ФМС, с точностью до 0.1% совпадают, что обосновывает приближение работы [3]. Однако вблизи концов полуосей верхнего эллипсоида на участке порядка 0.1a поле ${{H}_{x}}$ резко возрастает меняет знак и достигает на вершине эллипсоида значения H_x(a) = 152.77 Э. Среднего значения вдоль большей оси верхнего эллипсоида посчитанное по формуле (7) равно H_xcp = –10.23 Э. Если формально посчитать параметр r в (2), введенный в работе [5], по формуле

(9)

$r = \frac{{{{H}_{{xср}}}}}{{{{H}_{{m1}}}}},$

получим значение r = 0.88.

Для второго случая, когда длина и ширина полосок в десять раз меньше (a = 0.3 мкм, b = 0.1 мкм), из рис. 2б следует, что неоднородность поля ${{H}_{x}}$ внутри верхнего эллипсоида значительно больше. Размагничивающее поле внутри нижнего эллипсоида H_m1x = –113.13 Э. Поле в центре верхнего эллипсоида, порожденное намагниченным нижним эллипсоидом, равно H_x(0) = –107.29 Э и отличается на 5% от ${{H}_{{m1x}}},$ на вершине эллипсоида значения H_x(а) = 350.04 Э. Среднего значения вдоль большей оси верхнего эллипсоида равно H_xcp = –73.92 Э. Параметр (9) в этом случае будет иметь значение r = 0.65.

Из приведенных данных следует, что если СМС и ФМС ЗЭ идентичны, то на глубине порядка 10% от вершины СМС (больших полюсов верхнего эллипсоида на рис. 1) имеется сильная неоднородность в распределении намагниченности, которая может влиять не переключение СТМР ЗЭ. Чтобы избавиться от этой особенности достаточно СМС уменьшить в размере приблизительно на 10%.

ОБЛАСТЬ БИСТАБИЛЬНОГО КВАЗИРАВНОВЕСНОГО СОСТОЯНИЯ СМС

Области бистабильного квазиравновесного состояния однородно намагниченной эллипсоидальной частицы во внешнем магнитном поле ${{\vec {H}}_{0}}$ для различных конкретных физических задач исследовалась во многих работах [1, 3–5]. Проведем аналогичные исследования в рассматриваемых случаях с учетом неоднородности магнитного поля ФМС (поля, создаваемого вектором намагниченности нижнего эллипсоида на рис. 1). Будем полагать, что распределение векторов намагниченности в полосках однородно. Тогда плотность магнитной энергии СМС (в верхнем эллипсоиде рис. 1) можно представить в виде

(10)

$w = {{w}_{z}} + {{w}_{{an}}} + {{w}_{m}} + {{w}_{c}}.$

Здесь ${{w}_{z}}$ – плотность магнитной энергии, обусловленная внешним полем ${{\vec {H}}_{0}}$ (энергия Зеемана)

(11)

${{w}_{z}} = - {{\vec {M}}_{2}}{{\vec {H}}_{0}},$

${{w}_{{an}}}$ – плотность магнитной энергии одноосной анизотропии

(12)

${{w}_{{an}}} = K{{\sin }^{2}}\varphi ,$

где $K$ – константа одноосной анизотропии, ось которой направлена вдоль координатной оси X, $\varphi $ – угол между вектором намагниченности ${{\vec {M}}_{2}}$ и направлением координатной оси X. Выражение (12) часто записывают через константу “поле анизотропии”

(13)

${{H}_{{an}}} = \frac{{2K}}{M},$

где

(14)

$M = \left| {{{{\vec {M}}}_{1}}} \right| = \left| {{{{\vec {M}}}_{2}}} \right|.$

С учетом обозначения (13) формула (12) примет вид

(15)

${{w}_{{an}}} = \frac{{{{H}_{{an}}}M}}{2}{{\sin }^{2}}\varphi .$

Третье слагаемое в (10) ${{w}_{m}}$ – плотность магнитостатической энергии

(16)

${{w}_{m}} = - \frac{{{{{\vec {H}}}_{m}}{{{\vec {M}}}_{2}}}}{2},$

где ${{\vec {H}}_{m}}$ – размагничивающее поле эллипсоида, компоненты которого определяются выражениями

(17)

${{H}_{{mx}}} = - 4\pi {{n}_{x}}{{M}_{{2x}}},\,\,\,\,{{H}_{{my}}} = - 4\pi {{n}_{y}}{{M}_{{2y}}},$

${{n}_{x}}$ и ${{n}_{y}}$ – размагничивающие коэффициенты эллипсоида [7]

(18)

${{n}_{x}} = \frac{{abc}}{2}\int\limits_0^\infty {\frac{{dt}}{{({{a}^{2}} + t)R(t)}}} ,\,\,\,\,{{n}_{y}} = \frac{{abc}}{2}\int\limits_0^\infty {\frac{{dt}}{{({{b}^{2}} + t)R(t)}}} .$

Последнее слагаемое в (10) ${{w}_{с}}$ – плотность магнитостатической энергии взаимодействия с магнитостатическим полем ФМС (магнитным полем нижнего эллипсоида на рис. 1). В отличие от работ [3–5, 8] учтем влияние неоднородности этого поля. Для простоты ограничимся вычислением этой энергии вблизи большей оси симметрии эллипсоида, т.е. в узком цилиндре радиуса $\varepsilon $ и высотой $2a,$ в пределах которого поле можно считать совпадающим с полем на оси симметрии, имеющим одну ненулевую компоненту ${{H}_{x}}$ равную выражению (7). Тогда энергия взаимодействия с этой областью будет равна

(19)

${{W}_{c}} = - \int\limits_{ - a}^a {{{M}_{{2x}}}{{H}_{x}}} dx\pi {{\varepsilon }^{2}} = - {{M}_{{2x}}}{{H}_{{xa{{\nu }}}}}\pi {{\varepsilon }^{2}} \cdot 2a,$

где

(20)

${{H}_{{xa{{\nu }}}}} = \frac{1}{{2a}}\int\limits_{ - a}^a {{{H}_{x}}} dx.$

Из (19) для плотности энергии взаимодействия получим

(21)

${{w}_{с}} = \frac{{{{W}_{c}}}}{{\pi {{\varepsilon }^{2}}2a}} = - {{M}_{{2x}}}{{H}_{{xa{{\nu }}}}}.$

Принимая во внимание соотношения

(22)

$\begin{gathered} {{M}_{{2x}}} = M\cos \varphi ,\,\,{{M}_{{2y}}} = M\sin \varphi , \\ {{{\vec {H}}}_{0}} = ({{H}_{{0x}}},{{H}_{{0y}}},0) \\ \end{gathered} $

и формул (13)–(21), получим следующую зависимость плотности магнитной энергии (10) от угла поворота $\varphi $ вектора намагниченности ${{\vec {M}}_{2}}$ относительно оси координат X

(23)

$\begin{gathered} w(\varphi ) = M\left[ { - ({{H}_{{0x}}} + {{H}_{{xa{{\nu }}}}})\cos \varphi - {{H}_{{0y}}}\sin \varphi + } \right. \\ \left. { + \,\,\frac{{{{H}_{{an}}} + 4\pi {{n}_{y}}M}}{2}{{{\sin }}^{2}}\varphi + 2\pi {{n}_{x}}M{{{\cos }}^{2}}\varphi } \right]. \\ \end{gathered} $

Плотность энергии (23) в зависимости от величин компонент внешнего поля ${{H}_{{0x}}},$ ${{H}_{{0y}}}$ и среднего магнитостатического поля ${{H}_{{xa{{\nu }}}}}$ может иметь два локальных минимума (бистабильное состояние) или один минимум (одно устойчивое состояние ориентации вектора ${{\vec {M}}_{1}}$). При возрастании компонент внешнего магнитного поля ${{H}_{{0x}}},$ ${{H}_{{0y}}},$ при фиксированном угле $\varphi ,$ при некоторых их значениях бистабильное состояние пропадает и возникает одно устойчивое состояние. Математически это означает, что при бистабильном состоянии функция (23) имеет три экстремума: два локальных минимума и один максимум. Критические значения параметров ${{H}_{{0x}}},$ ${{H}_{{0y}}},$ при котором пропадает бистабильное состояние, означает слияние одного локального минимума функции (23) с максимумом и образование точки перегиба. Значение компонент ${{H}_{{0x}}},$ ${{H}_{{0y}}},$ при которых возникает такое состояние, можно определить из условий [8]

(24)

$\frac{{\partial w(\varphi )}}{{\partial \varphi }} = 0,\,\,\,\,\frac{{{{\partial }^{2}}w(\varphi )}}{{{{\partial }^{2}}\varphi }} = 0.$

Дифференцируя функцию (23) получим

(25)

$\begin{gathered} {{H}_{{0x}}} + {{H}_{{xa{{\nu }}}}} = - ({{H}_{{an}}} + 4\pi M({{n}_{y}} - {{n}_{x}})){{\cos }^{3}}\varphi , \\ {{H}_{{0y}}} = ({{H}_{{an}}} + 4\pi M({{n}_{y}} - {{n}_{x}})){{\sin }^{3}}\varphi . \\ \end{gathered} $

При изменении угла $\varphi $ от 0 до 2π уравнения (25) будут вычерчивать на плоскости замкнутую кривую астроиду, кривая инверсии, которую впервые получили Стонер и Вольфарт [1, 8].

Определим минимальное импульсное магнитное поле ${{H}_{0}}$ способное переключать рассмотренные ячейки MRAM. Для этого запишем соотношения (25) в безразмерной форме, вводя безразмерные величины

$\begin{gathered} {{{\bar {H}}}_{{0x}}} = \frac{{{{H}_{{0x}}}}}{{{{H}_{{an}}} + 4\pi M({{n}_{y}} - {{n}_{x}})}}, \\ {{{\bar {H}}}_{{0y}}} = \frac{{{{H}_{{0y}}}}}{{{{H}_{{an}}} + 4\pi M({{n}_{y}} - {{n}_{x}})}}, \\ {{{\bar {H}}}_{{xa{{\nu }}}}} = \frac{{{{H}_{{xa{{\nu }}}}}}}{{{{H}_{{an}}} + 4\pi M({{n}_{y}} - {{n}_{x}})}}, \\ \end{gathered} $

тогда вместо (25) получим

(26)

${{\bar {H}}_{{0x}}} = - {{\bar {H}}_{{xa{{\nu }}}}} - {{\cos }^{3}}\varphi ,\,\,\,\,{{\bar {H}}_{{0y}}} = {{\sin }^{3}}\varphi .$

Модуль безразмерного вектора напряженности внешнего поля будет равен

(27)

${{\bar {H}}_{0}} = \sqrt {\bar {H}_{{0x}}^{2} + \bar {H}_{{0y}}^{2}} = \sqrt {{{{({{{\bar {H}}}_{{xa{{\nu }}}}} + {{{\cos }}^{3}}\varphi )}}^{2}} + {{{\sin }}^{6}}\varphi } .$

Дифференцируя выражение (27) по $\varphi $ и приравнивая производную к нулю находим два различных значения $\cos \varphi ,$ при которых расстояние до различных участков кривой инверсии будет минимальным

(28)

$\cos {{\varphi }_{{1,2}}} = \frac{{ - {{{\bar {H}}}_{{xa{{\nu }}}}} \pm \sqrt {{{{({{{\bar {H}}}_{{xa{{\nu }}}}})}}^{2}} + 8} }}{4}.$

Для рассмотренных выше элементов ячеек MRAM ${{\bar {H}}_{{xa{{\nu }}}}}$ равно –0.1577 (для a = 3 мкм, b = = 1 мкм) и –0.1513 (для a = 0.3 мкм, b = 1 мкм), т.е. практически совпадают.

(29)

$\cos {{\varphi }_{1}} = 0.7476,\,\,\,\,{{\varphi }_{{\text{1}}}} = {\text{41}}.{\text{6}}^\circ ,$

(30)

$\cos {{\varphi }_{2}} = - 0.6687,\,\,\,\,{{\varphi }_{{\text{2}}}} = {\text{131}}.{\text{9}}^\circ .$

Подставляя (29), (30) в выражения (26), (27), находим

(31)

${{\bar {H}}_{{0x1}}} = - 0.260,\,\,\,\,{{\bar {H}}_{{0у1}}} = 0.292,\,\,\,\,{{\bar {H}}_{{01}}} = 0.414;$

(32)

${{\bar {H}}_{{0x2}}} = 0.457,\,\,\,\,{{\bar {H}}_{{0у2}}} = 0.411,\,\,\,\,{{\bar {H}}_{{02}}} = 0.614.$

Умножая значения (31), (32) на размерный множитель ${{H}_{{an}}} + 4\pi M({{n}_{y}} - {{n}_{x}}),$ принимающий для рассматриваемых двух полосок СМС значения 64.9 и 488.6 Э, получим следующие оптимальные физические значения компонент напряженности поля переключающих ориентацию вектора ${{\vec {M}}_{2}}$ в СМС:

для первой полоски с (a = 3 мкм, b = 1 мкм)

(33)

${{H}_{{0x1}}} = - 17\,\,{\text{Э}},\,\,\,\,{{H}_{{0у1}}} = 19\,\,{\text{Э,}}\,\,\,\,{{H}_{{01}}} = 25\,\,{\text{Э}};$

(34)

${{H}_{{0x2}}} = 30\,\,{\text{Э}},\,\,\,\,{{H}_{{0у2}}} = 27\,\,{\text{Э}},\,\,\,\,{{H}_{{02}}} = 40\,\,{\text{Э}};$

для второй полоски с (a = 0.3 мкм, b = 0.1 мкм)

(35)

${{H}_{{0x1}}} = - 129\,\,{\text{Э}},\,\,\,\,{{H}_{{0у1}}} = 144\,\,{\text{Э,}}\,\,\,\,{{H}_{{01}}} = 194\,\,{\text{Э}};$

(36)

${{H}_{{0x2}}} = 221\,\,{\text{Э}},\,\,\,\,{{H}_{{0у2}}} = 200\,\,{\text{Э}},\,\,\,\,{{H}_{{02}}} = 298\,\,{\text{Э}}{\text{.}}$

ЗАКЛЮЧЕНИЕ

Таким образом, в работе исследовано влияние неоднородности магнитного поля ФМС СТМР ЗЭ на переключение ориентаций вектора ${{\vec {M}}_{2}}$ СМС. Установлено, что вблизи границ магнитной полоски СМС неоднородность магнитного поля, обусловленная намагниченностью ФМС, достигает существенной величины, а магнитное поле на границе резко возрастает по сравнению с центральной частью полоски. При уменьшении размеров полосок неоднородность магнитного поля возрастает в объеме всей полоски. Показано, что при условии однородности распределения вектора намагниченности по объему полоски, эту неоднородность можно учесть посредством введения среднего поля. Это обосновывает модель развитую в [5] и позволяет вычислять эмпирический коэффициент, введенный в этой работе. Найдены оптимальные значения импульса магнитного поля, переключающие битовые состояния для рассмотренных СТМР ЗЭ.

Список литературы

Ikegawa S. // IEEE T. Electron Dev. 2020. V. 67. No. 4. P. 1407.
Parkin S.S.P., Roche K.P., Samant M.G. et al. // J. Appl. Phys. 1999. V. 85. No. 8. P. 5828.
Worledge D.C. // Appl. Phys. Lett. 2004. V. 84. No. 15. P. 2847.
Worledge D.C. // Appl. Phys. Lett. 2004. V. 84. No. 22. P. 4559.
Wang S., Fujiwara H., Sun M. // J. Magn. Magn. Mater. 2005. No. 295. P. 246.
Стрэттон Дж. Теория электромагнетизма. М.–Л.: ГИТТЛ, 1948. 539 с.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. Теоретическая физика. Т. 8. М.: Наука, 1982. 620 с.
Stoner E.C., Wohlfarth E.P. // IEEE Trans. Magn. 1991. V. 27. No. 4. P. 3475.
Абрамовиц М., Стиган И. Справочник по специальным функциям с формулами графиками и таблицами. М.: Наука, 1979. 832 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал