Известия РАН. Серия физическая, 2021, T. 85, № 12, стр. 1720-1726
Волновые пучки в активных периодических структурах с квадратичной нелинейностью
М. В. Комиссарова 1, И. Г. Захарова 1, *, Т. М. Лысак 1, А. А. Калинович 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”
Москва, Россия
* E-mail: zaharova@physics.msu.ru
Поступила в редакцию 05.07.2021
После доработки 26.07.2021
Принята к публикации 27.08.2021
Аннотация
Исследованы особенности формирования параметрических оптических солитонов в допированной активными элементами брэгговской структуре с квадратичной нелинейностью. С помощью численного моделирования продемонстрировано, что конкуренция нелинейной связи, брэгговского отражения и дополнительного профиля усиления/поглощения приводит, в целом, к асимметричной картине распространения двухчастотных солитонов.
ВВЕДЕНИЕ
Важным фактором, влияющим на особенности распространения волн в периодических структурах (ПС), является наличие или отсутствие консервативности системы. В последнее время в центре внимания исследователей находятся активные искусственные ПС, т.е. такие структуры, в которых консервативность нарушена. Изготовить подобную структуру возможно путем допирования основного материала какими-либо активными элементами, например ионами редкоземельных металлов. Такой подход используется, например, при создании структур с симметрией четность-время, так называемых PT- (parity-time) симметричных ПС. Дополнительный профиль усиления/поглощения, возникающий за счет чередования слоев из усиливающих и поглощающих материалов, обуславливает необычные асимметричные свойства оптических сред с PT-симметрией. Применение PT-симметричных ПС открывает новые возможности в управлении, усилении и генерации оптического излучения, поэтому исследования по данной теме весьма актуальны.
В отличие от непериодических структур, распространение излучения в линейных ПС приводит к возникновению запрещенной полосы частот, что в свою очередь порождает обратные волны. Несмотря на энергетические потери в ПС за счет поглощения, возможно компенсировать их и даже использовать для создания новых оптических устройств.
Инициированные в работе [1] в 1998 г. исследования PT-симметрии, оформились как чрезвычайно активная и плодотворная научная область, имеющая теоретическое, экспериментальное и коммерческое применение. В PT-симметричных оптических системах возможно достижение энергетического баланса поглощения и усиления, поскольку волна усиливается в некоторых областях системы и ослабляется в других [2].
Оптические системы в параксиальном приближении описываются системами уравнений типа Шредингера. Поэтому их можно рассматривать как PT-симметричные системы, считая диэлектрическую проницаемость аналогом комплексного потенциала, причем условие PT-симметрии имеет вид: $\varepsilon \left( r \right) = \,\,~\varepsilon ~*( - r)$ [2–4].
Последнее условие означает, что для вещественной и мнимой частей проницаемости верно Re[ε(–r)] = Re[ε(r)], ${\text{Im}}[\varepsilon ( - r)] = - {\text{Im}}[\varepsilon (r)]{\text{,}}$ тем самым, в среде присутствуют и поглощение, и усиление.
PT-симметричные оптические системы интенсивно изучаются многими авторами (см., например, обзор [2], а также [5–7]. Даже в линейном случае оптическая PT-симметричная структура обладает необычными свойствами в окрестности запрещенной полосы частот. К интересным эффектам можно отнести наблюдаемое в [8, 9] полное поглощение отраженного излучения. В системе с нарушенной PT-симметрией при достаточно сильном поглощении и усилении возможна генерация светового излучения. Это явление легло в основу конструкции PT-симметричного лазера [10, 11].
При увеличении интенсивности падающего излучения необходимо учитывать нелинейные эффекты. Как правило, исследуются PT-системы с керровской нелинейностью [12, 13]. Среди описанных нелинейных эффектов следует отметить генерацию оптических солитонов [14] и возможность оптической бистабильности в активных средах [15, 16].
Рассмотрение сред с квадратичной нелинейностью представляет безусловный интерес для исследователей в связи с более низким порогом по интенсивности проявления нелинейных явлений.
Периодические структуры с квадратичной нелинейностью интенсивно исследуются последние 20 лет. Отметим, что даже в пассивной структуре (где нет поглощения/усиления) картина протекания нелинейных волновых взаимодействий гораздо сложнее, нежели в среде с кубичной нелинейностью. Это обусловлено тем, что любой процесс в периодической среде с квадратичной нелинейностью представляет из себя конкуренцию между традиционным параметрическим взаимодействием волн с различными частотами и взаимодействием прямой и обратной волн одной частоты [17].
Такие процессы, как генерация второй гармоники, невырожденное трехчастотное взаимодействие, а также генерация субгармоники протекают при конкуренции между традиционным параметрическим взаимодействием волн с различными частотами и взаимодействием прямой и обратной волн.
В настоящей работе с помощью численного моделирования анализируется процесс распространения оптического излучения в среде с квадратичной нелинейностью и симметрией четность-время. Исследование проводится на основе оригинальной модели, учитывающей дифракцию. Более простые системы уравнений без учета дифракции и в пассивной среде изучались в работах [18, 19].
ПОСТАНОВКА ЗАДАЧИ
Рассмотрим генерацию второй гармоники (ГВГ) фемтосекундным лазерным излучением в планарной периодической диэлектрической структуре, описываемой следующей зависимостью диалектрической проницаемости [20]
(1)
$\begin{gathered} \varepsilon (z) = {{\varepsilon }_{0}} + {{\Delta }}{{\varepsilon }_{R}}{\text{cos}}\left( {\frac{{2\pi }}{d}z} \right) + i{{\Delta }}{{\varepsilon }_{I}}{\text{sin}}\left( {\frac{{2\pi }}{d}z} \right) + \\ + \,\,{{\Delta }}{{\varepsilon }_{{R2}}}{\text{cos}}\left( {\frac{{4\pi }}{d}z} \right) + i{{\Delta }}{{\varepsilon }_{{I2}}}{\text{sin}}\left( {\frac{{4\pi }}{d}z} \right) \\ \end{gathered} $от координаты распространения z. В выражении (1) d-период брэгговской структуры, первое слагаемое ε0 описывает среднее значение диэлектрической проницаемости, а амплитуды остальных слагаемых малы, $\Delta {{\varepsilon }_{R}},\Delta {{\varepsilon }_{{{{R}_{2}}}}}$ и $\Delta {{\varepsilon }_{I}},\Delta {{\varepsilon }_{{{{I}_{2}}}}}$ – амплитуды изменения вещественной и мнимой частей диэлектрической проницаемости соответственно для излучения на основной и удвоенной частотах.
Распространение оптического излучения в такой структуре в предположении когерентности излучения, усреднения по координате y и в пренебрежении дисперсией может быть описано с помощью волнового уравнения [21]
(2)
$\frac{{{{\partial }^{2}}E}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}E}}{{\partial {{x}^{2}}}} - \frac{{\varepsilon (z)}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}E}}{{\partial {{t}^{2}}}} = \frac{{4\pi }}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}P}}{{\partial {{t}^{2}}}},$(3)
$\begin{gathered} i\left( {\frac{{\partial {{E}_{{1 + }}}}}{{\partial z}} + \frac{{\partial {{E}_{{1 + }}}}}{{\partial \tau }}} \right) + {{D}_{{x,1}}}\frac{{{{\partial }^{2}}{{E}_{{1 + }}}}}{{\partial {{x}^{2}}}} + \delta {{E}_{{1 + }}} + (\kappa + g){{E}_{{1 - }}} + \\ + \,\,E_{{1 + }}^{{\text{*}}}{{E}_{{2 + }}} = 0,\,\,\,\,i\left( { - \frac{{\partial {{E}_{{1 - }}}}}{{\partial z}} + \frac{{\partial {{E}_{{1 - }}}}}{{\partial \tau }}} \right) + {{D}_{{x,1}}}\frac{{{{\partial }^{2}}{{E}_{{1 - }}}}}{{\partial {{x}^{2}}}} + \\ + \,\,\delta {{E}_{{1 - }}} + (\kappa - g){{E}_{{1 + }}} + E_{{1 - }}^{{\text{*}}}{{E}_{{2 - }}} = 0, \\ i\left( {\frac{{\partial {{E}_{{2 + }}}}}{{\partial z}} + \nu \frac{{\partial {{E}_{{2 + }}}}}{{\partial \tau }}} \right) + {{D}_{{x,2}}}\frac{{{{\partial }^{2}}{{E}_{{2 + }}}}}{{\partial {{x}^{2}}}} + {{\delta }_{2}}{{E}_{{2 + }}} + \\ + \,\,\left( {{{\kappa }_{2}} + {{g}_{2}}} \right){{E}_{{2 - }}} + {{\sigma }}{{\left( {{{E}_{{1 + }}}} \right)}^{2}} = 0, \\ i\left( { - \frac{{\partial {{E}_{{2 - }}}}}{{\partial z}} + \nu \frac{{\partial {{E}_{{2 - }}}}}{{\partial \tau }}} \right) + {{D}_{{x,2}}}\frac{{{{\partial }^{2}}{{E}_{{2 - }}}}}{{\partial {{x}^{2}}}} + {{\delta }_{2}}{{E}_{{2 - }}} + \\ + \,\,\left( {{{\kappa }_{2}} - {{g}_{2}}} \right){{E}_{{2 + }}} + {{\sigma }}{{\left( {{{E}_{{1 - }}}} \right)}^{2}} = 0. \\ \end{gathered} $Отметим, что аналогичная система была получена в работах [18, 19] в пассивной среде и без учета дифракции по переменной x. В работе [20] были получены аналогичные уравнения без учета генерации второй гармоники и дифракции.
В уравнениях (3) $\delta = {{({{k}_{1}} - \alpha )} \mathord{\left/ {\vphantom {{({{k}_{1}} - \alpha )} {{{l}_{{nl}}}}}} \right. \kern-0em} {{{l}_{{nl}}}}},$ ${{\delta }_{2}} = {{({{k}_{2}} - 2\alpha )} \mathord{\left/ {\vphantom {{({{k}_{2}} - 2\alpha )} {{{l}_{{nl}}}}}} \right. \kern-0em} {{{l}_{{nl}}}}}$ – отстройки от брэгговского резонанса на основной и удвоенной частотах, ${{\Delta }}k = {{k}_{2}} - 2{{k}_{1}}$ – расстройка фазовых скоростей, ${{k}_{{1,2}}}$ – волновые числа на основной и удвоенной частотах, $\alpha = \frac{\pi }{d},$ z – переменная, вдоль которой распространяется излучение, измеряется в единицах нелинейной длины ${{l}_{{nl}}} = {{\left( {{{\gamma }_{1}}\sqrt {{{I}_{1}}} } \right)}^{{ - 1}}}$$\left( {z \to z{{l}_{{nl}}}} \right),$ x – поперечная переменная, измеряется в единицах поперечной ширины пучка ${{a}_{x}}(x \to {x \mathord{\left/ {\vphantom {x {{{a}_{x}}}}} \right. \kern-0em} {{{a}_{x}}}}),$ $\tau = \frac{t}{\eta }{{l}_{{nl}}}$ – безразмерное время, связанное с физическим временем t соотношением, $\eta = \frac{{{{\varepsilon }_{0}}{{\omega }_{0}}}}{{{{c}^{2}}{{k}_{1}}}} = \frac{{\sqrt {{{\varepsilon }_{0}}} }}{c},$ с учетом $k_{1}^{2} = \frac{{{{\varepsilon }_{0}}}}{{{{c}^{2}}}}\omega _{0}^{2},$ ${{\omega }_{0}}$ – частота брэгговского резонанса. $\kappa = \frac{{\omega _{0}^{2}}}{{{{c}^{2}}{{k}_{1}}}}\frac{{{{\Delta }}{{\varepsilon }_{R}}}}{4}\frac{1}{{{{l}_{{nl}}}}}$ = = $\frac{{{{\omega }_{0}}}}{{c\sqrt {{{\varepsilon }_{0}}\left( {{{\omega }_{0}}} \right)} }}\frac{{{{\Delta }}{{\varepsilon }_{R}}}}{4}\frac{1}{{{{l}_{{nl}}}}},$ ${{\kappa }_{2}} = \frac{{4\omega _{0}^{2}}}{{{{c}^{2}}{{k}_{2}}}}\frac{{{{\Delta }}{{\varepsilon }_{{R2}}}}}{4}\frac{1}{{{{l}_{{nl}}}}}$ = $\frac{{2{{\omega }_{0}}}}{{c\sqrt {{{\varepsilon }_{0}}\left( {2{{\omega }_{0}}} \right)} }}\frac{{{{\Delta }}{{\varepsilon }_{{R2}}}}}{4}\frac{1}{{{{l}_{{nl}}}}}$ – параметры брэгговской связи. $g = \frac{{\omega _{0}^{2}}}{{{{c}^{2}}{{k}_{1}}}}\frac{{{{\Delta }}{{\varepsilon }_{I}}}}{4}\frac{1}{{{{l}_{{nl}}}}}$ = $\frac{{{{\omega }_{0}}}}{{c\sqrt {{{\varepsilon }_{0}}} }}\frac{{{{\Delta }}{{\varepsilon }_{I}}}}{4}\frac{1}{{{{l}_{{nl}}}}},$ ${{g}_{2}} = \frac{{4\omega _{0}^{2}}}{{{{c}^{2}}{{k}_{2}}}}\frac{{{{\Delta }}{{\varepsilon }_{{I2}}}}}{4}\frac{1}{{{{l}_{{nl}}}}}$ = $\frac{{2{{\omega }_{0}}}}{{c\sqrt {{{\varepsilon }_{0}}(2{{\omega }_{0}})} }}\frac{{{{\Delta }}{{\varepsilon }_{{I2}}}}}{4}\frac{1}{{{{l}_{{nl}}}}}$ – параметры несимметричной связи между встречными волнами. ${{\gamma }_{1}} = \frac{{4\pi }}{{{{c}^{2}}{{k}_{1}}}}\omega _{0}^{2}{{\chi }^{{(2)}}}$$( - {{\omega }_{0}},2{{\omega }_{0}}),$ ${{\gamma }_{2}} = \frac{{8\pi }}{{{{c}^{2}}{{k}_{2}}}}$$\omega _{0}^{2}{{\chi }^{{(2)}}}({{\omega }_{0}},{{\omega }_{0}})$ – коэффициенты квадратичной нелинейности, где ${{\chi }^{{(2)}}}$ – нелинейная восприимчивость среды, $\sigma = {{{{\gamma }_{2}}} \mathord{\left/ {\vphantom {{{{\gamma }_{2}}} {{{\gamma }_{1}}}}} \right. \kern-0em} {{{\gamma }_{1}}}}$ – их отношение; ${{D}_{{x,1}}} = {{\left( {2{{k}_{1}}{{l}_{{nl}}}a_{x}^{2}} \right)}^{{ - 1}}},$ ${{D}_{{x,2}}} = {{\left( {2{{k}_{2}}{{l}_{{nl}}}a_{x}^{2}} \right)}^{{ - 1}}}$ – дифракционные параметры для волны на основной и удвоенной частоте, соответственно.
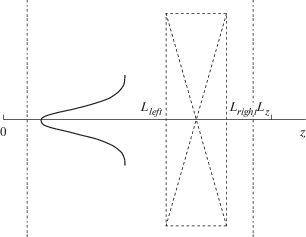
Мы предполагаем, что периодическая среда окружена однородной линейной средой с диэлектрической проницаемостью ${{\varepsilon }_{0}},$ в которой можно пренебречь расплыванием пучка за счет дифракции (рис. 1). Тем самым распространение лазерного излучения в такой среде (при $0 < x < {{L}_{x}}$ и $0 < z < {{L}_{{left}}},$ ${{L}_{{right}}} < z < {{L}_{z}}$) описывается уравнениями (3), в левой части которых оставлены только два первых слагаемых.
На границах рассматриваемых областей ставятся граничные условия
(4)
$\begin{gathered} {{E}_{{1 + }}}(z = 0,x,\tau ) = {{E}_{{2 + }}}(z = 0,x,\tau ) = \\ = {{E}_{{1 - }}}(z = {{L}_{z}},x,\tau ) = {{E}_{{1 - }}}(z = {{L}_{z}},x,\tau ) = 0, \\ {{E}_{{1 \pm }}}(z,x = 0,\tau ) = {{E}_{{2 \pm }}}(z,x = 0,\tau ) = \\ = {{E}_{{1 \pm }}}(z,x = {{L}_{x}},\tau ) = {{E}_{{2 \pm }}}(z,x = {{L}_{x}},\tau ) = 0, \\ \end{gathered} $при $\tau = 0$ задается начальное условие
(5)
$\begin{gathered} {{E}_{{1 + }}}(z,x,\tau = 0) = {{E}_{{10}}}(z,x),\,\,\,\,{{E}_{{2 + }}}(z,x,\tau = 0) = \\ = {{E}_{{20}}}(z,x),\,\,\,\,{{E}_{{10}}}(z = 0) = {{E}_{{10}}}(z = {{L}_{{left}}}) = 0. \\ \end{gathered} $Рассмотрим падение на периодическую структуру излучения на основной частоте в виде пучка, имеющего солитонный профиль, при отсутствии излучения на частоте второй гармоники
(6)
$\begin{gathered} {{E}_{{10}}}(z,x) = {{A}_{{10}}}c{{h}^{{ - 1}}}\left( {{{\left( {z - \frac{{{{L}_{{left}}}}}{2}} \right)} \mathord{\left/ {\vphantom {{\left( {z - \frac{{{{L}_{{left}}}}}{2}} \right)} {{{h}_{z}}}}} \right. \kern-0em} {{{h}_{z}}}}} \right) \times \\ \times \,\,c{{h}^{{ - 1}}}\left( {{{\left( {x - \frac{{{{L}_{x}}}}{2}} \right)} \mathord{\left/ {\vphantom {{\left( {x - \frac{{{{L}_{x}}}}{2}} \right)} {{{h}_{x}}}}} \right. \kern-0em} {{{h}_{x}}}}} \right),\,\,\,\,{{E}_{{20}}}(z,x) = 0. \\ \end{gathered} $Параметры ${{h}_{z}}$ и ${{h}_{x}}$ характеризуют ширину пучка в продольном и поперечном направлении, соответственно.
Уравнения (3)–(6) решаются численно с использованием консервативной нелинейной разностной схемы на характеристической сетке, реализуемой с помощью итерационного алгоритма.
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Численные расчеты в настоящей работе проводились для следующих значений безразмерных параметров, которые соответствуют окрестности нижней границы брэгговской щели:
(7)
$\begin{gathered} \kappa = 1,\,\,\,\,{{\kappa }_{2}} = {{g}_{2}} = 0,\,\,\,\,\delta = - 0.9,\,\,\,\,{{\delta }_{2}} = 5, \\ \sigma = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},\,\,\,\,{{A}_{{10}}} = \sqrt {10} ,\,\,\,\,{{h}_{z}} = 5,\, \\ \end{gathered} $Для параметров (7) ранее [18] было продемонстрировано формирование брэгговских солитонов на основной частоте и частоте второй гармоники в пассивной 1D полубесконечной периодической среде, причем формирование солитонов происходило как для прямых волн, так и для отраженных волн.
Можно показать, что учет конечной ширины пучка в поперечном направлении (вдоль переменной x), а также активная среда оказывают существенное влияние на формирование и распространение брэгговских солитонов. Рисунки 2, 3 и 4 демонстрируют особенности формирования солитонов при учете конечной ширины пучка в поперечном направлении для пассивной среды ($g = 0,$ рис. 2) и двух активных сред, различающихся порядком поглощающих и генерирующих слоев: $g = 1$ (рис. 3) и $g = - 1$ (рис. 4).
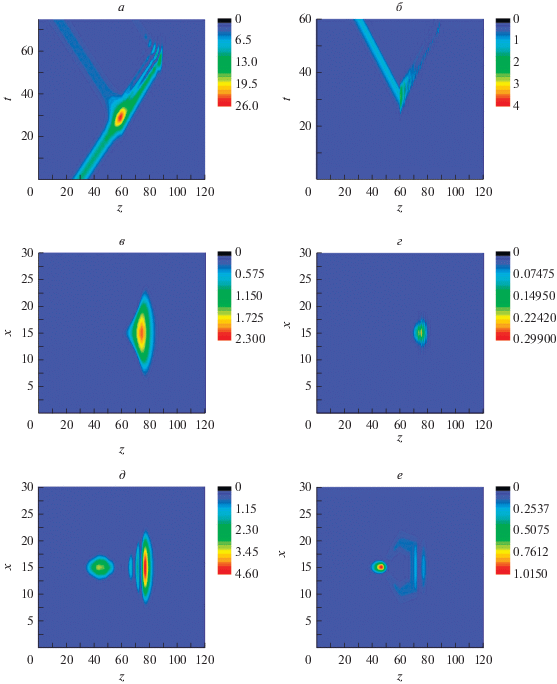
Рис. 2.
Формирование брэгговских солитонов для волны на основной частоте (а) и частоте второй гармоники (б) для пассивной среды ($g = 0$). Профиль пучка прямой волны на основной частоте (в) и удвоенной частоте (г), обратной волны на основной частоте (д) и удвоенной частоте (е) в момент времени $\tau = 45.$
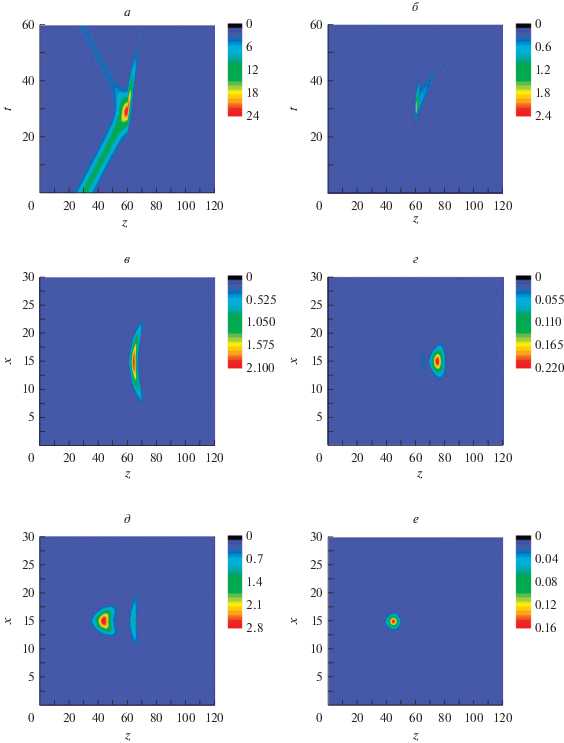
Рис. 3.
Формирование брэгговских солитонов для волны на основной частоте (а) и частоте второй гармоники (б) для активной среды ($g = 1$). Профиль падающего пучка на основной частоте (в). Профиль пучка прямой волны на основной частоте (кривая 1) и удвоенной частоте (кривая 2) в центральном сечении ($x = 15$) в момент времени $\tau = 60{\text{\;}}$ (г).
Сравнение с результатами работы [18], показывает, что учет конечной ширины пучка в поперечном направлении качественно не изменяет характер, приводя преимущественно к трансформации исходного солитонного пучка к серповидной форме. Заметим, что серповидная форма пучка прямой волны на основной частоте отражается также в форме пучков остальных трех волн: отраженной волны на основной частоте и обеих волн на удвоенной частоте.
Наличие активных компонентов периодической структуры приводит к существенной трансформации картины формирующихся солитонов. Причем критически важным в этом случае является порядок чередования поглощающих и усиливающих слоев. В частности, при $g = 1$ (рис. 3) обратные волны не формируются. Действительно, в этом случае $\kappa - g = {{\kappa }_{2}} - {{g}_{2}} = 0,$ поэтому во втором и четвертом уравнениях отсутствует генерирующие слагаемые.
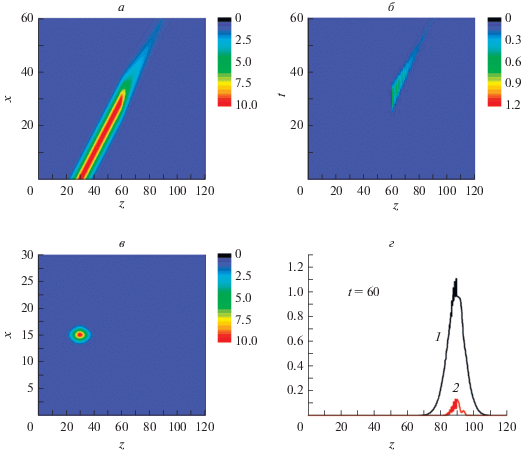
При ином чередовании активных и пассивных слоев, картина формирования солитонов существенно изменяется. Помимо отражения основной волны от передней границы периодической структуры наблюдается также отражение от задней границы (рис. 4а). В результате на основной частоте формируется обратная волна, состоящая из нескольких субпучков (рис. 4г), тогда как распространение остальных волны близко к солитоноподобному.
ЗАКЛЮЧЕНИЕ
Рассмотрены особенности формирования брэгговских солитонов в пассивных и активных средах в условиях генерации второй гармоники при учете конечной ширины пучка в поперечном направлении. Установлено, что порядок чередования усиливающих и поглощающих слоев в активной периодической структуре оказывает существенное влияние на процесс формирования солитонов прямой и обратной волны на основной и удвоенной частотах. Показано, что изменением чередования генерирующих и поглощающих слоев можно добиться как усиления пропускания излучения через периодическую структуру, так и усиления отражения излучения от границ периодической структуры.
Исследование выполнено при поддержке Междисциплинарной научно-образовательной школы Московского государственного университета “Фотонные и квантовые технологии. Цифровая медицина”.
Список литературы
Bender C.M., Boettcher S. // Phys. Rev. Lett. 1998. V. 80. P. 5243.
Зябловский А.А., Виноградов А.П., Пухов А.А. и др. // УФН. 2014. Т. 184. № 11. С. 1177; Zyablovsky A.A., Vinogradov A.P., Pukhov A.A. et al. // Phys. Usp. 2014. V. 57. No. 11. P. 1063.
Makris G., El-Ganainy R., Christodoulides D.N., Musslimani Z.H. // Phys. Rev. Lett. 2008. V. 100. Art. No. 103904.
Ruter C.E., Makris G., El-Ganainy R. et al. // Nat. Phys. 2010. V. 10. P. 192.
Suchkov S.V., Sukhorukov A.A., Huang J. et al. // Laser Photon. Rev. 2016. V. 10. P. 1.
Konotop V.V., Yang J., Zezyulin D.A. // Rev. Modern Phys. 2016. V. 88. No. 3. Art. No. 035002.
El-Ganainy R., Makris K.G., Khajavikhan M. et al. // Nature Phys. 2018. V. 14. P. 11.
Feng L., Xu Y.-L., Fegadolli W.S. et al. // Nature Mater. 2013. V. 12. P. 108.
Feng L., Zhu X., Yang S. et al. // Opt. Expr. 2014. V. 22. No. 2. P. 1760.
Gu J., Xi X., Ma J., Yu Z., Sun X. // Sci. Rep. 2016. V. 6. Art. No. 37688.
Longhi S. // Sci. Rep. 2010. V. 82. No. 3. Art. No. 031801.
Li K., Zezyulin D.A., Kevrekidis P.G. et al. // Phys. Rev. A. 2013. V. 88. Art. No. 053820.
Ögren M., Abdullaev F.Kh., Konotop V.V. // Opt. Lett. 2017. V. 42. No. 20. P. 4079.
Miri M.-A., Aceves A.B., Kottos T. et al. // Phys. Rev. A. 2012. V. 86. No. 3. Art. No. 033801.
Liu J., Xie X.-T., Shan C.-J. et al. // Laser Phys. 2015. V. 25. Art. No. 015102.
Phang S., Vukovic A., Susanto H. et al. // Opt. Lett. 2014. V. 39. No. 9. P. 2603.
Манцызов Б.И. ГВГ в фотонных кристаллах. Когерентная и нелинейная оптика фотонных кристаллов. М.: Физматлит, 2009.
Conti C., Assanto G., Trillo S. // Opt. Lett. 1997. V. 22. No. 17. P. 1350.
Conti C., Assanto G., Trillo S. // Phys. Rev. Lett. 1997. V. 78. P. 2341.
Komissarova M.V., Marchenko V.F., Shestakov P.Yu. // Phys. Rev. E. 2019. V. 99. No. 4. Art. No. 042205.
Pelinovsky D., Sears J., Brzozowski L., Sargent E.H. // J. Opt. Soc. Amer. B. 1997. V. 19. P. 43.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая