Известия РАН. Серия физическая, 2021, T. 85, № 12, стр. 1770-1775

ВВЕДЕНИЕ

Многокомпонентные среды, такие как коллоидные растворы, суспензии наночастиц, активно применяются для реализации различных нелинейно-оптических процессов: от лазерной абляции до динамической голографии [1–11]. В частности, нерезонансный характер термодиффузионной и электрострикционной нелинейностей [11–14] позволяет применять их с использованием широкого диапазона длин волн в четырехволновых преобразователях излучения, которые осуществляют обращение волнового фронта падающей (сигнальной) волны [15]. При этом важно знать не только коэффициент отражения преобразователя (или дифракционную эффективность записываемой голограммы) [7, 14], но и степень соответствия пространственного распределения амплитуды волны с обращенным волновым фронтом (объектной волны) распределению амплитуды сигнальной волны [16].

К настоящему времени проведен анализ вида пространственного спектра объектной волны (ПСОВ) при четырехволновом взаимодействии (ЧВВ) в прозрачных суспензиях наночастиц в зависимости от интенсивности [17], угла падения и расходимости волн накачки [18, 19], соотношения их длин волн [15]. При этом пренебрегалось силой тяжести, действующей на наночастицы.

В коллоидных растворах энергия теплового движения молекул жидкости сравнима с энергией растворенных наночастиц, находящихся в гравитационном поле Земли [20–23]. В работе [24] показано, что поток наночастиц, вызванный силой тяжести, может существенно влиять на эффективность преобразования низких пространственных частот сигнальной волны. При этом считалось, что волны накачки распространяются навстречу друг другу в вертикальной плоскости, т.е. коллинеарно силе тяжести.

В настоящей работе в зависимости от массы наночастиц в прозрачной суспензии анализируется вид ПСОВ, образующейся в процессе ЧВВ в схеме с горизонтально распространяющимися волнами накачки.

МОДЕЛЬ ЧЕТЫРЕХВОЛНОВОГО ВЗАИМОДЕЙСТВИЯ

Рассмотрено вырожденное ЧВВ в вертикальном плоском слое прозрачной суспензии наночастиц, заключенном между плоскостями z = 0 и z = $\ell $ [18]. Первая волна накачки и сигнальная волна с комплексными амплитудами A₁ и A₃, соответственно, падают на переднюю грань, а вторая волна накачки с амплитудой A₂ – на заднюю. В приближениях заданного поля по волнам накачки и малого коэффициента преобразования в случае, когда волна A₂ некогерентна с волнами A₁ и A₃, интенсивность излучения I, распространяющегося в нелинейной среде, может быть представлена в виде суммы интенсивностей волн накачки и слагаемых, обусловленных интерференцией волн A₁ и A₃ [24, 25]

Наличие градиента интенсивности вследствие диффузии, электрострикции и действия поля тяжести Земли приводит к изменению в пространстве концентрации наночастиц δС, растворенных в жидкости [15, 26, 27]. Из-за возникающего потока частиц вследствие эффекта Дюфура изменяется также температура среды δT. Таким образом, в среде записывается фазовая решетка, обусловленная при малых начальных концентрациях наночастиц вкладом в изменение показателя преломления в основном изменения температуры [12, 14, 28, 29]. В результате дифракции второй волны накачки возникает объектная волна с амплитудой A₄, волновой фронт которой комплексно-сопряжен (обращен) по отношению к фронту сигнальной волны [24].

Вырожденное ЧВВ в прозрачной среде описывается уравнением Гельмгольца вида [16, 19]

где $k = {{2{{\pi }}{{n}_{l}}} \mathord{\left/ {\vphantom {{2{{\pi }}{{n}_{l}}} {{\lambda }}}} \right. \kern-0em} {{\lambda }}}{\text{,}}$ n_l – показатель преломления жидкости в отсутствие излучения, λ – длина волны взаимодействующих волн, $\left( {{{dn} \mathord{\left/ {\vphantom {{dn} {dT}}} \right. \kern-0em} {dT}}} \right)$ – термооптический коэффициент.

Уравнение (2) дополняется системой стационарных материальных уравнений диффузии и теплопроводности, учитывающих поле тяжести Земли [24]

Здесь D₁₁ – коэффициент теплопроводности, D₁₂ – коэффициент, характеризующий эффект Дюфура, D₂₂ – коэффициент диффузии, γ – коэффициент, характеризующий явление электрострикции [25], m – эффективная масса одной наночастицы в жидкости с поправкой на силу Архимеда, $\vec {g}$ – ускорение свободного падения, k_B – постоянная Больцмана, T₀ – начальная температура суспензии.

Величина γ пропорциональна поляризуемости наночастиц, которая определяется их показателем преломления, а также показателем преломления жидкости n_l [26, 28].

Рассматривались плоские волны накачки, распространяющиеся строго вдоль оси z навстречу друг другу [24]. Их амплитуды на гранях слоя среды равны соответственно A₁₀ и A₂₀. Система координат выбрана таким образом, чтобы сила тяжести была сонаправлена с осью x. В соответствии с выражением (1), описывающим распределение интенсивности излучения в среде, изменения концентрации δC и температуры δT представлялись в виде суммы медленно и быстро меняющихся в зависимости от поперечных координат x и y составляющих [25]. Сигнальная и объектная волны раскладывались по плоским волнам ${{\tilde {A}}_{3}}\left( {{{\vec {\chi }}}} \right)$ и ${{\tilde {A}}_{4}}\left( {{{\vec {\chi }}}} \right),$ а быстро меняющиеся составляющие δC и δT – по гармоническим решеткам ${{\delta }}\tilde {C}\left( {{{\vec {\chi }}}} \right)$ и ${{\delta }}\tilde {T}\left( {{{\vec {\chi }}}} \right)$ (где ${{\vec {\chi }}}$ – пространственная частота, проекция волнового вектора объектной волны на плоскость xy) [19].

При условии равенства нулю амплитуды объектной волны на задней грани нелинейного слоя выражение, описывающее в параксиальном приближении ($\left| {{{\vec {\chi }}}} \right| \ll k$) связь ПСОВ на передней грани ${{\tilde {A}}_{{40}}}\left( {{{\vec {\chi }}}} \right) = {{\tilde {A}}_{4}}\left( {{{\vec {\chi }}},z = 0} \right)$ со спектром температурной решетки ${{\delta }}\tilde {T}$ имеет вид [24, 25]

где P – фазовый набег, связанный с распространением в среде волн накачки.

ПРОСТРАНСТВЕННЫЙ СПЕКТР ОБЪЕКТНОЙ ВОЛНЫ

Для получения явного вида ${{\tilde {A}}_{{40}}}\left( {{{\vec {\chi }}}} \right)$ необходимо было найти выражения вначале для пространственного спектра концентрационной, а затем и температурной решеток. При этом материальные уравнения (3) и (4) с учетом сделанных выше приближений переписывались в виде

Здесь ${{\tilde {A}}_{{30}}}\left( {{{\vec {\chi }}}} \right) = {{\tilde {A}}_{3}}\left( {{{\vec {\chi }}},z = 0} \right)$ – пространственный спектр сигнальной волны на передней грани нелинейного слоя [18].

Система уравнений (6), (7) дополняется граничными условиями отсутствия полного потока наночастиц через грани слоя и неизменности на гранях температуры [19, 25, 30, 31]

С учетом условий (8) и (9) пространственный спектр решетки ${{\delta }}\tilde {T}$ можно записать следующим образом [24]

где ${{{{\lambda }}}_{{1,2}}}\left( {{{\vec {\chi }}}} \right)$ = $ \pm \sqrt {{{{{{\vec {\chi }}}}}^{2}} - i\frac{m}{{{{k}_{B}}{{T}_{0}}}}\left( {\vec {g},{{\vec {\chi }}}} \right)} ,$ ${{{{\lambda }}}_{3}}\left( {{{\vec {\chi }}}} \right) = - i\frac{{{{{{{\vec {\chi }}}}}^{2}}}}{{2k}},$ ${{{{\lambda }}}_{{4,5}}}{\kern 1pt} \left( {{{\vec {\chi }}}} \right)$ = $ \pm \left| {{{\vec {\chi }}}} \right|,$

В результате подстановки выражения (10) в (5) получена аналитическая связь пространственных спектров сигнальной и объектной волн на передней грани нелинейного слоя прозрачной суспензии наночастиц при вырожденном встречном ЧВВ

Выражение (11) по форме записи схоже с выражением для ПСОВ, представленным в работе [24], однако записано для схемы ЧВВ с горизонтально распространяющимися волнами накачки. В случае пренебрежимо малой эффективной массы одной наночастицы m оно совпадает с ПСОВ, полученным без учета поля тяжести Земли, действующего на наночастицы [17, 18].

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО АНАЛИЗА

В качестве прозрачной двухкомпонентной среды рассмотрена водная (n_l = 1.333) суспензия наночастиц при начальной температуре T₀= 300 К. Длина волны взаимодействующих волн λ = 532 нм. Считалось, что сигнальная волна распространяется от точечного источника, расположенного на передней грани среды (${{\tilde {A}}_{{30}}}\left( {{{\vec {\chi }}}} \right) = {\text{const}}$) [17, 18].

На рис. 1 приведены модули ПСОВ на передней грани слоя нелинейной среды толщиной $\ell $ = = 1 мм. В случае, когда эффективная масса одной наночастицы мала (рис. 1а), в модуле ПСОВ на низких пространственных частотах наблюдается провал, имеющий аксиальную симметрию, т.е. $\left| {{{{\tilde {A}}}_{{40}}}} \right|$ зависит только от модуля пространственной частоты ${{\vec {\chi }}} = \left\{ {{{{{\chi }}}_{x}},{{{{\chi }}}_{y}}} \right\}$ (где ${{{{\chi }}}_{x}},{{{{\chi }}}_{y}}$ – проекции вектора ${{\vec {\chi }}}$ на оси x и y, соответственно). Вид модуля ПСОВ является типичным для прозрачных суспензий наночастиц [17, 19]. С увеличением пространственной частоты величина $\left| {{{{\tilde {A}}}_{{40}}}} \right|$ монотонно возрастает, а затем выходит на постоянное значение

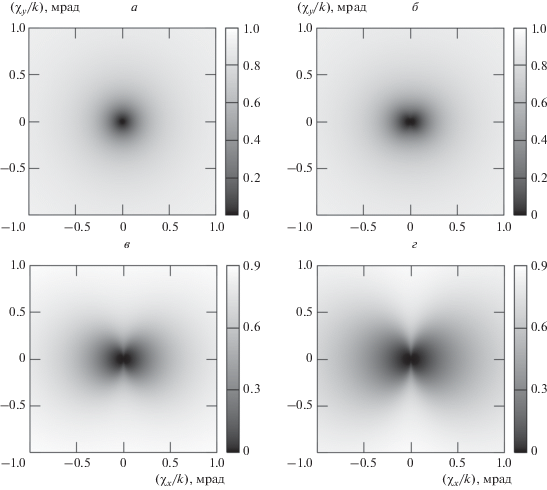
Выражение (12) совпадает с представленным в работе [17] для случая, когда поле тяжести, действующее на наночастицы в жидкости, не учитывалось.

В отличие от схемы с вертикально распространяющимися волнами накачки [24] при учете поля тяжести Земли не наблюдается возникновения максимума в модуле ПСОВ вблизи нулевой частоты. Если проекция χ_y = 0, то с увеличением массы одной наночастицы происходит уширение провала вдоль оси χ_x (рис. 1б), а при некотором отклонении χ_y от нуля – его раздваивание (рис. 1в, 1г). При этом в направлении оси χ_y при χ_x = 0 изменений в структуре и ширине провала не наблюдается. Такое нарушение аксиальной симметрии связано с отмеченной выше коллинеарностью вектора $\vec {g}$ оси x.

Численный анализ выражения (11) показывает, что при смене знака проекции g_x изменения вида модуля ${{\tilde {A}}_{{40}}}$ не происходит.

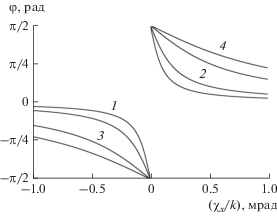
Рассмотрим теперь фазу ПСОВ при χ_y = 0 (рис. 2). На пространственной частоте χ_x → 0 происходит скачок фазы на π. При малых значениях эффективной массы одной наночастицы характер изменения фазы в зависимости от χ_x близок к гиперболическому. С ростом m в представленном диапазоне χ_x эта зависимость стремится к линейному закону. В целом же зависимость фазы (φ) в ветвях кривых рис. 2 от проекции пространственной частоты и массы одной наночастицы описывается выражением

Для анализа влияния поля тяжести Земли на пространственную структуру объектной волны введена полуширина провала $\Delta {{\chi }}$ [24] в модуле ПСОВ, которая определялась из решения уравнения вида [17]

На рис. 3 приведены зависимости полуширины провала от эффективной массы одной наночастицы при различных толщинах слоя водной суспензии. С увеличением m величина $\Delta {{\chi }}$ монотонно возрастает с последующим выходом на зависимость, близкую к линейной

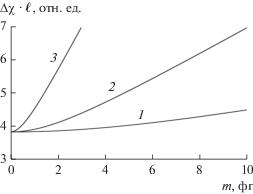
В выражении (15) коэффициент α в представленном диапазоне $\ell $ от 0.1 до 1 мм не зависит от толщины слоя и равен 8.68 ⋅ 10^–5 фг^–1, а коэффициент β определяется величиной полуширины провала в случае, когда эффективная масса наночастицы пренебрежимо мала, и с ростом толщины слоя уменьшается по закону ${{\ell }^{{ - 1}}}$. В частности, при $\ell $ = 0.1, 0.3 и 1 мм, значения β равны соответственно 1.8, 0.58 и 0.18 мрад.

Обратно пропорциональная зависимость коэффициента β от толщины среды подтверждается аналогичной зависимостью, полученной без учета поля тяжести Земли, действующего на наночастицы в прозрачной жидкости [17]. Следует отметить, что в работе [24], в которой поле тяжести учитывалось, также получена линейная зависимость вида (15) полуширины провала от эффективной массы одной наночастицы для больших значений m.

ЗАКЛЮЧЕНИЕ

Получено аналитическое выражение, связывающее ПСОВ с пространственным спектром сигнальной волны на передней грани слоя прозрачной суспензии наночастиц в процессе вырожденного ЧВВ в схеме, в которой встречные волны накачки распространяются ортогонально направлению поля тяжести Земли. Показано, что в противоположность схеме с волнами накачки, распространяющимися в вертикальной плоскости [24], при учете поля тяжести в схеме с горизонтально распространяющимися волнами накачки не наблюдается возникновения максимума модуля амплитуды объектной волны в области низких пространственных частот.

Рост эффективной массы одной наночастицы приводит к увеличению полуширины провала, возникающего в модуле ПСОВ в направлении, коллинеарном направлению поля тяжести. Это увеличение сопровождается монотонным выходом на зависимость, близкую к линейной. При этом, как и в случае вертикального распространения волн накачки [24], коэффициент пропорциональности не меняется с увеличением толщины среды.

Установлено, что характер изменения фазы ПСОВ вдоль направления поля тяжести описывается функцией арктангенса от отношения ${{{{k}_{B}}{{T}_{0}}{{{{\chi }}}_{x}}} \mathord{\left/ {\vphantom {{{{k}_{B}}{{T}_{0}}{{{{\chi }}}_{x}}} {m{{g}_{x}}}}} \right. \kern-0em} {m{{g}_{x}}}},$ где в числителе находится пространственная частота объектной волны, а в знаменателе – величина, характеризующая проекцию силы тяжести, действующей на наночастицы. При этом на нулевой пространственной частоте фаза испытывает скачок на π.

Полученные результаты могут быть полезны при проектировании систем нелинейной адаптивной оптики на основе прозрачных суспензий наночастиц для задач коррекции мелкомасштабных фазовых искажений сигнальной волны.