Известия РАН. Серия физическая, 2021, T. 85, № 5, стр. 749-752

ВВЕДЕНИЕ

Оценивание нормированных вариаций функций распределения интенсивноситей потоков мюонов (ФРИПМ) является актуальной задачей для физики космических лучей и техники мюонной диагностики [1, 2]. Матричные наблюдения мюонного годоскопа УРАГАН [3] (МГ)–ФРИПМ $Y(i,j,Tk)$ определяются для $i = 1,...,{{N}_{1}}$, $j = 1,...,{{N}_{2}}$, ${{N}_{1}} = 90$, ${{N}_{2}} = 76$, $T$-шаг по времени, $k = 1,2,...$ и могут считаться выходными для МГ. Индексы $i,j$ задают азимутальные и зенитные углы ${{\varphi }_{i}} = \Delta \varphi (i - 1)$, ${{\vartheta }_{j}} = \Delta \vartheta (j - 1)$, $\Delta \varphi = 1^\circ $, $\Delta \vartheta = 4^\circ $. Входные ФРИПМ для МГ обозначаются как ${{Y}_{0}}(i,j,Tk)$.

МГ-наблюдения содержат особенности из-за различных вариантов модуляций потоков мюонов (ПМ). Первый вариант модуляций обусловливается конструкцией МГ, второй – метеовозмущениями, третий – зависимостью уровнем шумов в МГ-наблюдениях от зенитных углов.

В данной работе предложен метод оценивания нормированных вариаций функций интенсивностей ПМ на основе временных рядов матричных МГ-наблюдений для распознавания в них локальных анизотропий (ЛА).

МЕТОД ОЦЕНИВАНИЯ НОРМИРОВАННЫХ ВАРИАЦИЙ ФРИПМ ДЛЯ РАСПОЗНАВАНИЯ ЛОКАЛЬНЫХ АНИЗОТРОПИЙ

Возможны четыре подхода к задаче распознавания ЛА. Первый подход подразумевает распознавание непосредственно на основе выходных ФРИПМ $Y(i,j,Tk)$, $k = 1,2,...$. Однако, из-за значительных модуляций по сравнению с величинами ЛА, его реализация проблематична.

Второй подход предполагает оценивание ЛА на основе оценок $Y_{0}^{^\circ }(i,j,Tk)$ с использованием $Y(i,j,Tk)$, $k = 1,2,...$ и т.н. аппаратной функции (АФ) [4] $F(i,j,Tk)$. Входная ФРИМП ${{Y}_{0}}(i,j,Tk)$ и выходная $Y(i,j,Tk)$, при условии линейности МГ, связываются на основе соотношения

В общем случае АФ $F(i,j,Tk) = {{F}_{0}}(i,j){{F}_{w}}(j,Tk)$ представляет собой произведение функции ${{F}_{0}}(i,j)$, зависящей от конструкции МГ, и ${{F}_{W}}(j,Tk)$, моделирующей метеомодуляции. Оценки $Y_{0}^{^\circ }(i,j,Tk)$ из (1) могут определяться путем решения обратной задачи. С учетом (1) получим

где $F^\circ (i,j)$-оценка АФ. Из (2) следует, что точному оцениванию входной ФРИПМ и распознаванию ЛА [5], препятвуют погрешности в оценках АФ $F^\circ (i,j)$, шумы в выходных ФРИПМ и возможные малые значения ЛА.

Третий подход подразумевает введение эталонного и текущих временных участков, на которых вычисляются доверительные интервалы [6] для математических ожиданий МГ-наблюдений. Распознавание ЛА производится путем анализа расположений доверительных интервалов.

Четвертый подход альтернативен третьему. Распознавание на основе нормированных вариаций ФРИПМ осуществим в два этапа. На первом – рассмотрим $Y(i,j,Tk)$, $k = 1,...,{{k}_{{f1}}}$ и модельную АФ в виде ${{N}_{1}}$, ${{N}_{2}}$ параметров ${{f}_{{0,i\,j}}}$. Математические ожидания случайных $Y_{0}^{{}}(i,j,Tk)$ для телесных углов $i,j$ обозначим как ${{c}_{0}}$. ФРИПМ и АФ определим с точностью до множителя. Введем нормированную АФ $F_{N}^{{}}(i,j) = {{f}_{{ij}}}$ и функционал ${{S}_{0}}$, где ${{f}_{{ij}}} = {{f}_{{0,ij}}}{{c}_{0}}$

Параметры $f_{{ij}}^{^\circ }$ найдем путем минимизации функционала ${{S}_{0}}$ (3)

На втором этапе запишем разность $\delta Y^\circ (i,j,Tk)$ = = $Y(i,j,Tk) - F_{N}^{^\circ }(i,j)$, $k = {{k}_{{f1}}} + 1,...,{{k}_{{f1}}} + {{k}_{{f2}}}$. Величины шумов для $\delta Y^\circ (i,j,Tk)$ пропорциональны значениям АФ. Представим оценки нормированных вариаций выходных ФРИПМ $\delta Y_{N}^{^\circ }(i,j,Tk)$

Вычислим усредненную оценку нормированных вариаций ФРИПМ

Для снижения шумов в оценках (4), (5) и (6) применим скользящую двумерную фильтрацию [7]. С этой целью cформируем на прямоугольнике $({{N}_{1}},{{N}_{2}})$ систему аппроксимационных кусочно-линейных моделей размерности $(\Delta {{N}_{1}},\Delta {{N}_{2}})$ с шагами скольжения $({{N}_{{d1}}},{{N}_{{d2}}})$ и произведем их взвешенное усреднение. Результат фильтрации для $A_{N}^{^\circ }(i,j)$ представим как $F_{{N,{\text{Ф}}}}^{^\circ }(i,j) = F_{{N,{\text{Ф}}}}^{^\circ }(\Delta N,{{N}_{d}},i,j)$. При делении в (5) на $F_{{N,{\text{Ф}}}}^{^\circ }(i,j)$ для малых значений знаменателя возможны большие шумовые погрешности. Чтобы их снизить реализуем пороговую фильтрацию, результат которой обозначим, как $F_{{N,{\text{Ф}}1}}^{^\circ }(i,j) = F_{{N,{\text{Ф}}1}}^{^\circ }(\Delta N,{{N}_{d}},i,j)$, и который получим на основе соотношений $F_{{N,{\text{Ф}}1}}^{^\circ }(i,j) = F_{{N,{\text{Ф}}}}^{^\circ }(i,j)$, если $F_{{N,{\text{Ф}}}}^{^\circ }(i,j) > {{f}_{0}}$, $F_{{N,{\text{Ф}}1}}^{^\circ }(i,j) = {{f}_{0}}$, если $F_{{N,{\text{Ф}}}}^{^\circ }(i,j) \leqslant {{f}_{0}}$, где ${{f}_{0}}$ – порог. Аналогично отфильтруем нормированные вариации выходных ФРИМП.

ТЕСТИРОВАНИЕ МЕТОДА ОЦЕНИВАНИЯ НОРМИРОВАННЫХ ВАРИАЦИЙ ФРИПМ НА ЭКСПЕРИМЕНТАЛЬНЫХ МГ-НАБЛЮДЕНИЯХ

Тестирование производилось на МГ-наблюдениях ${{Y}_{E}}(i,j,Tk)$, $k = 1,...,{{k}_{{f1}}} + {{k}_{{f2}}}$ взятых из [8]. Для индексов $k = {{k}_{{f1}}} + 1,...,{{k}_{{f1}}} + {{k}_{{f2}}}$ были сформированы модулирующие функции $\mu (i,j,Tk) = \mu (i,j)$ c прямоугольной областью ЛА

где $\delta \mu $ – величина понижения для области ЛА. Реализовывались произведения

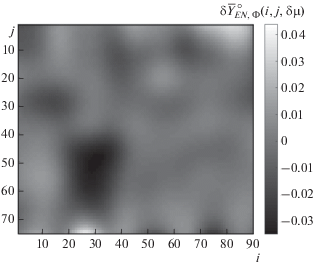
С использованием (4) на основе ${{Y}_{E}}(i,j,Tk)$, $k = 1,...,{{k}_{{f1}}}$, находилась оценка нормированной АФ $F_{{EN,{\text{Ф}}1}}^{^\circ }(i,j)$. Для ${{Y}_{E}}(i,j,Tk,\mu )$ и $F_{{EN,{\text{Ф}}1}}^{^\circ }(i,j)$, k = = ${{k}_{{f1}}} + 1,...,{{k}_{{f2}}}$ вычислялись $\delta Y_{{EN,{\text{Ф}}}}^{^\circ }(i,j,Tk,\mu )$, k_f1 = = 20, ${{k}_{{f2}}} = 20$, $\delta \mu = 0.03$$\,{{i}_{1}} = 20$, ${{i}_{2}} = 40$, ${{j}_{1}} = 40$, ${{j}_{2}} = 65$. На рис. 1 представлено 2D-изображение $\delta {{\bar {Y}}^{^\circ }}_{{ЕN,{\text{Ф}}1}}(i,j,\mu )$, с видимой областью ЛА-понижения. Вычислялись математические ожидания (м. о) и среднеквадратичные значения (СКЗ) для $\delta {{\bar {Y}}^{^\circ }}_{{ЕN,{\text{Ф}}1}}(i,j,\mu )$ с $\delta \mu = 0$ – $\sigma _{Е}^{^\circ } = 1.327 \cdot {{10}^{{ - 3}}}$; определялись м. о. и СКЗ для $\delta {{\bar {Y}}^{^\circ }}_{{ЕN,{\text{Ф}}}}(i,j,\mu )$ в области ЛА-понижения, получены $m_{Е}^{^\circ }(\delta \mu )$ = –0.0267, $\sigma _{Е}^{^\circ }(\delta \mu )$ = = 1.349 · 10^–4. Оценки $m_{Е}^{^\circ }(\delta \mu )$ были на порядок больше величины оценки $m_{Е}^{^\circ }$.

Метод оценивания нормированных вариаций ФРИПМ тестировался на задаче распознавания последовательности областей ЛА-понижений. Были сформированы матрицы экспериментальных МГ-наблюдений ${{Y}_{Е}}(i,j,Tk)$, $k = 1,...,{{k}_{{f1}}} + {{n}_{0}}{{k}_{{f2}}}$, ${{n}_{0}} = 12$. Для $k = 1,...,{{k}_{{f1}}}$ определялась оценка нормированной экспериментальной АФ $F_{{EN,{\text{Ф}}1}}^{^\circ }(i,j)$. Образовывались интервалы с точками ${{k}_{{n1}}} \leqslant k \leqslant {{k}_{{n2}}}$, k_n1 = = ${{k}_{{f1}}} + 1 + (n - 1){{k}_{{f2}}}$, ${{k}_{{n2}}} = {{k}_{{n1}}} + {{k}_{{f1}}} - 1$, $n = 1,...,{{n}_{0}}$; задавались по (7) функции $\mu (i,j,n)$, с $\delta \mu (n) = 0.005 + 0.005(n - 1)$, $n = 1,...6$, δμ(n) = 0.03 – – 0.005(n – 7) , $\,n = 7,...,{{n}_{0}}$,$\,{{i}_{1}} = 20$, ${{i}_{2}} = 40$, ${{j}_{1}} = 20$, ${{j}_{2}} = 45$. На рис. 2 представлены 2D-изображения последовательности $\delta {{\bar {Y}}^{^\circ }}_{{ЕN,{\text{Ф}}}}(i,j,\delta \mu (n))$; на кадрах с $n = 4{\kern 1pt} - {\kern 1pt} 9$ отчетливо видны области понижения – затемнения с ЛА, которые соответствуют $\delta \mu \approx 0.02{\kern 1pt} - {\kern 1pt} 0.03$.

ЗАКЛЮЧЕНИЕ

Предложенный метод оценивания нормированных вариаций ФРИПМ оказался эффективным и работоспособным. Исследование метода на экспериментальных МГ-наблюдениях показало, что оценки м. о. нормированных вариаций ФРИПМ для областей с ЛА на порядок превосходили оценки м. о. для областей без ЛА, что позволило сделать вывод о его благоприятных возможностях для распознавания ЛА. Распознавание последовательности ЛА-понижений уверенно реализовывалось для $\delta \mu = 0.02{\kern 1pt} - {\kern 1pt} 0.03$.

Работа выполнена при поддержке РНФ (проект № 17-17-01215-П).