Известия РАН. Серия физическая, 2021, T. 85, № 5, стр. 698-701

Изучение квантового хаоса затруднено отсутствием согласия по поводу самого понятия “квантового хаоса”. Это связано с тем, что после долгих поисков основного источника классического хаоса (см., например, [1]) было решено остановиться на ляпуновской неустойчивости траекторий хаотической системы к малым вариациям начальных условий. Действительно, при такой вариации траектории хаотической системы в фазовом пространстве расходятся по экспоненциальному закону exp(Λt), где Λ – показатель Ляпунова, определяющий скорость этого расхождения. Так как реальные начальные условия всегда задаются с конечной точностью, положение системы со временем делается совершенно непредсказуемым. Такую полную непредсказуемость движения системы называют динамическим хаосом.

Поскольку соотношение неопределенности в квантовой механике лишает понятие траектории необходимой точности, то классические критерии регулярности или хаоса, связанные с понятием траектории, делаются неприменимыми. Поэтому в настоящее время квантовый хаос принято определять как “динамику квантовых систем, являющихся хаотическими в классическом пределе”. Хотя это звучит весьма расплывчато, однако предлагается просто игнорировать вопрос об определении хаоса в квантовой механике, а вместо этого стараться определить свойства квантовых систем, соответствующие хаосу в классических системах. Пока что единственным таким свойством принято считать закон распределения энергетических уровней системы. Для квантовых аналогов хаотических систем распределение расстояний между уровнями близко к закону Вигнера с его характерным отталкиванием между уровнями. В соответствии с этим законом вероятность найти соседний уровень, отличающийся от данного на энергию $\varepsilon $ определяется выражением:

где $D$ – среднее расстояние между уровнями. Отталкиванием называется стремление к нулю вероятности найти соседний уровень при $\varepsilon \to 0.$

Для регулярных систем такого отталкивания не наблюдалось. Часто делаются утверждения, что распределение уровней для регулярных квантовых систем (т.е. для квантовых аналогов классических регулярных систем) описывается законом Пуассона:

В наших работах [2, 3] было показано, что закон Вигнера характеризует хаотическую систему только в том случае, когда рассматривается последовательность энергетических уровней с фиксированными значениями квантовых чисел (например спина и четности). Если отбора по спинам и четности не производить, то вигнеровское отталкивание уровней исчезает, хотя система остается хаотической. Именно поэтому распределение Пуассона никак не связано с регулярностью системы, а лишь свидетельствует о том, что мы не позаботились об отборе уровней с фиксированными спином и четностью, а “свалили в кучу” несколько независимых друг от друга последовательностей энергетических уровней. Поэтому закон распределения уровней не дает определения признаков регулярной квантовой системы и, следовательно, не позволяет оценивать степень хаотичности системы. А подобная оценка чрезвычайно необходима, поскольку теперь мы знаем, что практически все реальные физические системы в той или иной степени хаотичны.

Учитывая все вышеуказанное, мы предложили [2–7] использовать для определения классического и квантового хаоса теорему Лиувилля–Арнольда (Liouville–Arnold), хорошо известную в классической механике (см., например [8, 9]). Она утверждает, что система с N степенями свободы регулярна, если у нее есть M = N линейно-независимых первых интегралов движения, находящихся в инволюции. Первыми (глобальными) интегралами движения практически являются такие, которые по теореме Нетер (Noether) связаны с симметрией системы, т.е. с наличием группы преобразований, по отношению к которым гамильтониан системы инвариантен. Следует отметить, что не всегда закон сохранения (т.е. наличие первого интеграла движения системы) удается сразу связать с соответствующей ему симметрией. Например, закон сохранения вектора Лапласа–Рунге–Ленца в задаче Кеплера (задаче двух тел с потенциалом взаимодействия, обратно пропорциональным квадрату расстояния) был открыт еще в начале XVIII в., а его связь с группой вращения в четырехмерном пространстве SO(4) удалось обнаружить лишь в 30-е годы XX в.

В отличие от понятия траектории, применимого только в классической механике, понятие симметрии применимо для всех областей физики от классической механики до квантовой теории поля. Квантовым аналогом первого интеграла движения является “хорошее” квантовое число (собственное значение оператора, коммутирующего с гамильтонианом системы). Поэтому нам кажется естественным считать квантовой регулярной системой такую, гамильтониан которой обладает достаточно высокой симметрией, гарантирующей, что количество хороших квантовых чисел системы M не меньше числа ее степеней свободы N. Если внести в систему возмущающее взаимодействие, которое нарушит ее симметрию и уменьшит число хороших квантовых чисел так, что $M < N,$ система перестанет быть регулярной. Поэтому кажется естественным считать хаотической квантовую систему со столь низкой симметрией, что число ее хороших квантовых чисел меньше числа ее степеней свободы. Именно такое определение квантового хаоса и было предложено нами. Этот подход позволяет очень просто различать хаотическую и регулярную системы. В качестве количественной меры квантового хаоса мы используем заимствованную из теории нейтронных силовых функций величину ${{\Gamma }_{{spr}}}$ “размазки” компонент волновой функции регулярного состояния по состояниям той же системы, но в присутствии взаимодействия, нарушающего ее симметрию. Мы показали, что в предельном переходе к классической механике величина ${{{{\Gamma }_{{spr}}}} \mathord{\left/ {\vphantom {{{{\Gamma }_{{spr}}}} \hbar }} \right. \kern-0em} \hbar }$ переходит в показатель Ляпунова $\Lambda .$ С помощью этой величины мы рассмотрели количественный переход от регулярности к хаосу для квантовых аналогов единственных двух классических систем, для которых имеются количественные данные по аналогичным переходам – в системе Хенона–Хейлеса [10] и в диамагнитной задаче Кеплера [11, 12]. Использование предложенных нами методов показало, что и количественно переходы от квантовой регулярности к хаосу происходят аналогично классическим случаям.

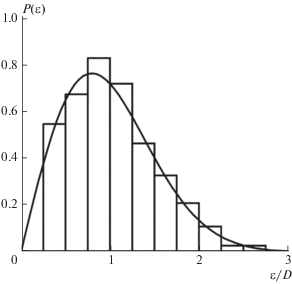
Однако в предложенном нами подходе возникают вопросы. Теорема Нетер, связывающая первые интегралы с симметриями гамильтониана, доказана лишь для непрерывных преобразований симметрии. Все первые интегралы в классической механике связаны именно с такими симметриями. Однако в квантовой механике существует и квантовое число четности по отношению к пространственной инверсии, а такое преобразование дискретно. Следует ли хорошее квантовое число (т.е. квантовый аналог первого интеграла) четности включать в число М первых интегралов при сравнении их с числом степеней свободы N если мы хотим использовать аналог теоремы Лиувилля–Арнольда в квантовом случае? В качестве наводящего соображения можно воспользоваться даже таким весьма несовершенным современным определением квантового хаоса как “динамики квантовых систем, являющихся хаотическими в классическом пределе”. Если первые интегралы, связанные с симметрией гамильтониана по отношению к непрерывным преобразованиям, сохраняются в предельном переходе от квантовой механики к классической, то квантовое число четности при этом просто исчезает. То есть число первых интегралов системы уменьшается. В то же время число степеней свободы системы при таком переходе остается неизменным. Значит при использовании аналога теоремы Лиувилля–Арнольда в квантовом случае включать четность в число М первых интегралов не следует. Для проверки этого предположения рассмотрим хорошо изученный случай двумерного биллиарда вида “стадион”. Под биллиардом понимается движение материальной точки в плоскости, ограниченной упруго отражающими стенками определенной формы. Границами стадиона являются два параллельных прямых отрезка, соединенных на концах двумя полуокружностями. В классической механике биллиард вида стадион является самым типичным представителем хаотических систем. В полном соответствии с теоремой Лиувилля–Арнольда, при двух степенях свободы (N = 2) эта система имеет только один первый интеграл движения – энергию (т.е. M = 1 < N). В квантовом случае стадион обладает еще и дискретными симметриями по отношению к отражениям относительно двух осей симметрии стадиона, а, следовательно, двумя хорошими квантовыми числами четности. Поэтому энергетические уровни такой квантовой системы распадаются на четыре независимых совокупности, определяемых квантовыми числами четности при отражении относительно каждой из осей симметрии: четно-четную (т.е. четную по отношению к каждой из двух осей), нечетно-четную, четно-нечетную и нечетно-нечетную. Гистограмма распределения расстояний между уровнями нечетно-нечетной совокупности, полученная в работе [13], приведена на рис. 1. Видно, что она прекрасно описывается вигнеровским распределением (сплошная линия) с характерным отталкиванием уровней. Как указывалось выше, такое распределение является единственным общепринятым в настоящее время признаком хаотичности квантовой системы. Следовательно, появление двух чисто квантовых интегралов движения, связанных с симметрией системы относительно дискретных преобразований пространственного отражения, совершенно не изменило хаотичности системы, наблюдавшейся в классической механике. Поэтому, как мы и предполагали, в приложении теоремы Лиувилля–Арнольда к квантовым системам следует сравнивать число степеней свободы N не с полным числом независимых первых интегралов (хороших квантовых чисел) М, а лишь с числом ${{M}_{{cl}}}$ “классических” первых интегралов системы, свойственных ей в классической механике.

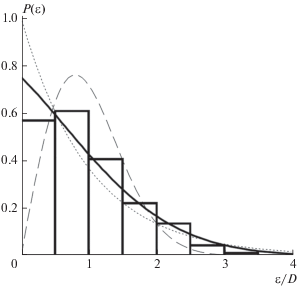
Любопытно отметить, что проведенное в работе [13] рассмотрение 600 нижних уровней квантового стадиона без разделения по квантовым числам четности (т.е. суперпозиции четырех независимых систем уровней) дает распределение уровней (см. рис. 2), резко отличающееся от вигнеровского отсутствием отталкивания уровней. Это лишний раз подтверждает, что такое отталкивание исчезает даже в распределении уровней квантовой хаотической системы, если не разделять совокупности уровней с отличающимися квантовыми числами.

Итак, мы пришли к выводу, что в приложении теоремы Лиувилля–Арнольда к квантовым системам следует сравнивать число степеней свободы N не с полным числом независимых первых интегралов (хороших квантовых чисел) М, а лишь с числом ${{M}_{{cl}}}$ “классических” первых интегралов системы, свойственных ей в классической механике. То есть дискретные преобразования (и вообще все специфически квантовые первые интегралы), исчезающие в классическом пределе, не следует учитывать, если мы хотим использовать аналог теоремы Лиувилля–Арнольда в квантовом случае. Если же пытаться по-прежнему определять хаотичность квантовой системы по наличию вигнеровского отталкивания в распределении уровней, то придется найти все эти “чисто-квантовые” интегралы движения (спин, четность и т.д.) и отбирать лишь энергетические уровни, с их фиксированным значением.