Известия РАН. Серия физическая, 2021, T. 85, № 5, стр. 662-670
Новый алгоритм вычисления протонных, нейтронных и зарядовых плотностей в ядрах: сравнение с экспериментальными данными
О. М. Сухарева 1, М. В. Чушнякова 1, И. И. Гончар 2, А. А. Климочкина 3, *
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Омский государственный технический университет”
Омск, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Омский государственный университет путей сообщения”
Омск, Россия
3 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”
Москва, Россия
* E-mail: klimann16@gmail.com
Поступила в редакцию 20.11.2020
После доработки 28.12.2020
Принята к публикации 27.01.2021
Аннотация
Плотность нуклонов – фундаментальная величина в ядерной физике. Она, в частности, является важным ингредиентом в модели двойной свертки при расчете сечений слияния ядер. Предложен упрощенный способ расчета этой плотности, основанный на микроскопических плотностях для шести реперных ядер. В отличие от микроскопических расчетов, предложенный метод не является трудоемким и может быть легко использован экспериментаторами.
ВВЕДЕНИЕ
Коллективное ядерное движение большой амплитуды, примерами которого являются слияние [1–5], деление [6–8] и квазиделение [3, 9, 10], представляет большой интерес как с экспериментальной, так и с теоретической точек зрения. В результате соответствующих экспериментов были синтезированы ядра с зарядовыми числами Z от 104 до 118 [11, 12].
В настоящей работе внимание сконцентрировано на процессе захвата ядер в орбитальное движение при их столкновении. Если произведение зарядовых чисел сталкивающихся ядер Z1 и Z2 не превосходит 1300, захват завершается слиянием [13], далее в тексте используется только этот термин.
Существует несколько методов для расчета сечений слияния. Метод Хартри–Фока с зависимостью от времени [14–16], являясь одним из наиболее реалистичных, реализуется с существенными ограничениями и требует значительных затрат компьютерных ресурсов. Менее требовательными к вычислительным мощностям методами являются, например, метод связанных каналов [17‒19] или траекторный анализ с учетом диссипации [20–22].
Важной частью любого из методов является процедура нахождения энергии сильного ядро-ядерного взаимодействия (СиЯВ) ${{U}_{n}}\left( R \right).$ Для расчета энергии СиЯВ часто используется параметризация потенциала формулой Вудса–Саксона (недостатком которой является привязка к экспериментальным данным: три независимых параметра этой формулы – глубина, радиус и диффузность – варьируются так, чтобы расчет воспроизводил экспериментальные сечения слияния при надбарьерных энергиях). Также могут быть использованы потенциал proximity и другие феноменологические потенциалы. В настоящее время часто предпочтение отдается более теоретически обоснованному методу двойной свертки (double folding) [23–27]. В этом методе энергия СиЯВ ${{U}_{n}}\left( R \right)$ вычисляется следующим образом:
(1)
${{U}_{n}}\left( R \right) = \int {d{{{\vec {r}}}_{1}}} \int {d{{{\vec {r}}}_{2}}{{\rho }_{{A1}}}\left( {{{r}_{1}}} \right){{\nu }_{{NN}}}} \left( {\left| {\vec {R} - {{{\vec {r}}}_{2}} + {{{\vec {r}}}_{1}}} \right|} \right){{\rho }_{{A2}}}\left( {{{r}_{2}}} \right).$Здесь ${{\vec {r}}_{1}}$ и ${{\vec {r}}_{2}}$ – радиус-векторы двух взаимодействующих точек (ядра-снаряда и ядра-мишени соответственно), $\vec {R}$ – вектор, соединяющий центры масс ядер, ${{\rho }_{{A1}}}\left( {{{r}_{1}}} \right)$ и ${{\rho }_{{A2}}}\left( {{{r}_{2}}} \right)$ – нуклонные плотности ядер, ${{\nu }_{{NN}}}$ – эффективный нуклон-нуклонный потенциал. В настоящей работе рассмотрены сферические сталкивающиеся ядра.
Оценки материальной плотности ядер в значительной степени опираются на экспериментальную информацию о зарядовых распределениях плотности [28–30]. В настоящее время эксперименты по измерению непосредственно нуклонной плотности немногочисленны [31–33] и имеют большие погрешности.
Теоретическое описание нуклонных плотностей ядер осуществляется во многих моделях, например в релятивистской модели среднего поля [34], в подходе Хартри–Фока [35–37]. Однако микроскопические расчеты весьма трудоемки. Расчет нуклонной плотности в одночастичном приближении с дисперсионными оптическими потенциалами является менее ресурсоемким [38, 39]. Наиболее популярной аппроксимацией радиальной зависимости плотности протонов ${{\rho }_{Z}}\left( {r{\text{\;}}} \right)$ и нейтронов ${{\rho }_{N}}\left( r \right)$ является распределение Ферми [25, 27, 40, 41]:
(2)
${{\rho }_{{ZF}}}\left( r \right) = {{\rho }_{{ZС}}}{{\left[ {1 + {\text{exp}}\left\{ {{{\left( {r - {{r}_{{Z0}}}{{A}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {r - {{r}_{{Z0}}}{{A}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right)} {{{a}_{Z}}}}} \right. \kern-0em} {{{a}_{Z}}}}} \right\}} \right]}^{{ - 1}}},$(3)
${{\rho }_{{NF}}}\left( r \right) = {{\rho }_{{NС}}}{{\left[ {1 + {\text{exp}}\left\{ {{{\left( {r - {{r}_{{N0}}}{{A}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right)} \mathord{\left/ {\vphantom {{\left( {r - {{r}_{{N0}}}{{A}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}} \right)} {{{a}_{N}}}}} \right. \kern-0em} {{{a}_{N}}}}} \right\}} \right]}^{{ - 1}}}.$В настоящей статье изложен упрощенный алгоритм расчета плотности нейтронов ${{\rho }_{N}}\left( r \right)$ и протонов ${{\rho }_{Z}}\left( r \right),$ основанный на известной плотности электрического заряда в ядре. Этот алгоритм может быть полезен экспериментаторам. Основа предложенного алгоритма – линейная интерполяция параметров плотности нуклонов для произвольного сферического ядра между определенными в этой работе параметрами для шести ядер, выбранных в качестве реперных.
АППРОКСИМАЦИЯ ПЛОТНОСТЕЙ ПРОФИЛЕМ ФЕРМИ С ЭКСПОНЕНЦИАЛЬНЫМ ХВОСТОМ (FE-АППРОКСИМАЦИЯ)
На первом этапе мы ставим своей целью аппроксимировать протонную ${{\rho }_{{ZSKX}}}\left( r \right)$ и нейтронную ${{\rho }_{{NSKX}}}\left( r \right)$ плотности реперных сферических ядер 12С, 16О, 36S, 92Zr, 144Sm, 204Pb, полученные с помощью метода Хартри–Фока с набором параметров SKX (HF SKX) в работе [36], фермиевскими функциями (2) и (3) соответственно.
Алгоритм нахождения параметров ${{\rho }_{{ZС}}},$ ${{r}_{{Z0}}},$ ${{a}_{Z}}$ (${{\rho }_{{NС}}},$ ${{r}_{{N0}}},$ ${{a}_{N}}$) опишем на примере плотности протонов.
В массиве значений протонной плотности ${{\rho }_{{ZSKX}}}\left( r \right)$ мы находим максимальное значение (оно должно быть близким по значению к ${{\rho }_{{ZSKX}}}\left( 0 \right),$ но не обязательно совпадает с ним, см., например, рис. 1а, 1г и рис. 2а). Это значение принимается за начальное значение ${{\rho }_{{ZCF}}}.$
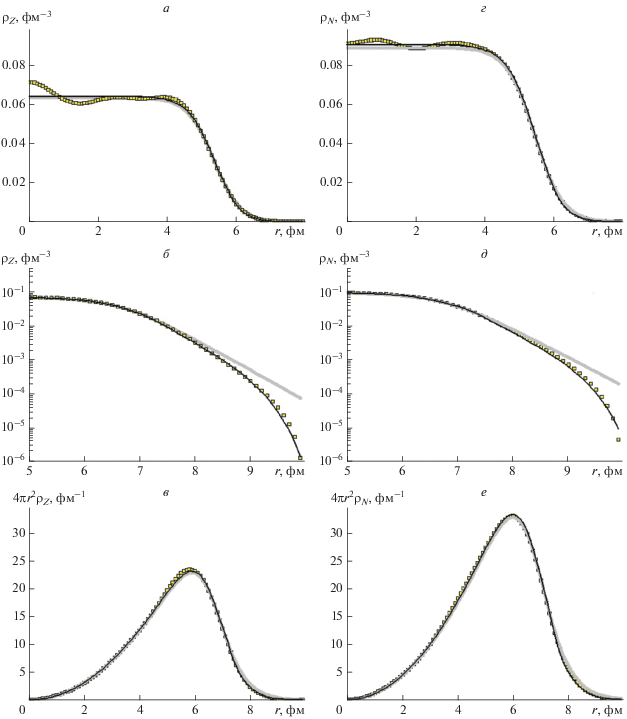
Рис. 1.
Зависимость протонной ${{\rho }_{Z}}\left( r \right)$ (а, б, в) и нейтронной ${{\rho }_{N}}\left( r \right)$ (г, д, е) плотностей от расстояния от центра ядра для 92Zr в линейном (а, г) и логарифмическом (б, д) масштабах, а также с множителем $4\pi {{r}^{2}}$ (в, е). Квадраты – микроскопический расчет HF SKX, толстые серые линии – F-аппроксимация, тонкие черные линии – результаты расчета по FE-алгоритму.
Далее определяется расстояние от центра ядра ${{R}_{Z}},$ на котором ${{\rho }_{{ZSKX}}}\left( {{{R}_{Z}}} \right) \approx {{{{\rho }_{{ZCF}}}} \mathord{\left/ {\vphantom {{{{\rho }_{{ZCF}}}} 2}} \right. \kern-0em} 2}$ (радиус половинной плотности ядра). Затем численно находится производная ${{d{{\rho }_{{ZSKX}}}} \mathord{\left/ {\vphantom {{d{{\rho }_{{ZSKX}}}} {dr}}} \right. \kern-0em} {dr}}$ при $r = {{R}_{Z}}.$ Легко показать, что
(4)
$\frac{{d{{\rho }_{{ZSKX}}}}}{{dr}}\left( {{{R}_{Z}}} \right) \approx - \frac{{{{\rho }_{{ZCF}}}}}{{4{{a}_{Z}}}}.$Соотношение (4) используется для определения диффузности ${{a}_{Z}}.$ Знаки приближенного, а не точного равенства обусловлены тем, что расчеты проводятся на сетке. Из связи ${{R}_{Z}} = {{r}_{{Z0}}}{{A}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}$ следует выразить ${{r}_{{Z0}}}.$ С полученными параметрами ${{\rho }_{{ZCF}}},$ ${{r}_{{Z0}}},$ ${{a}_{Z}}$ вычисляется протонная плотность ${{\rho }_{{ZF}}}\left( r \right)$ по формуле (2) в диапазоне от 0 до 10 фм с шагом 0.1 фм. Полученное распределение должно удовлетворять условию нормировки
однако на первом этапе, поскольку в качестве ${{\rho }_{{ZCF}}}$ выбрано максимальное значение плотности, правая часть (5) больше левой.
Далее действия, описанные в предыдущем абзаце, повторяются с постепенным уменьшением значения параметра ${{\rho }_{{ZCF}}}$ на 0.1% на каждом шаге. Окончательные значения параметров ${{\rho }_{{ZCF}}},$ ${{r}_{{Z0}}}$ и ${{a}_{Z}}$ соответствуют минимальной разности между правой и левой частями формулы (5). Такая же процедура применяется для нахождения параметров плотности нейтронов.
Таблица 1.
Параметры плотностей протонов и нейтронов для реперных ядер, а также относительные разности ${{\varepsilon }_{Z}}$ и ${{\varepsilon }_{N}}$ (см. формулу (8)). Количество значащих цифр соответствует 0.1%-ному изменению параметров ${{\rho }_{{ZCF}}}$ и ${{\rho }_{{NCF}}}$ (см. текст перед формулой (4))
| Ядро | 12C | 16O | 36S | 92Zr | 144Sm | 204Pb |
|---|---|---|---|---|---|---|
| ${{\rho }_{{ZCFE}}}$, фм–3 | 0.08277 | 0.07640 | 0.07205 | 0.06905 | 0.06679 | 0.06281 |
| ${{r}_{{Z0}}}$, фм | 1.006 | 1.061 | 1.074 | 1.111 | 1.131 | 1.133 |
| ${{a}_{Z}}$, фм | 0.4715 | 0.4706 | 0.4863 | 0.4916 | 0.4766 | 0.4748 |
| ${{\varepsilon }_{Z}},\% $ | 4.8 | 3.0 | 6.1 | 4.5 | 3.9 | 3.0 |
| ${{x}_{Z}} = {{x}_{N}}$ | 0 | 0 | 0.5 | 1 | 2 | 3 |
| ${{\rho }_{{NCFE}}}$, фм–3 | 0.08416 | 0.07766 | 0.08462 | 0.08624 | 0.08531 | 0.08843 |
| ${{r}_{{N0}}}$, фм | 1.001 | 1.056 | 1.096 | 1.125 | 1.142 | 1.152 |
| ${{a}_{N}}$, фм | 0.4687 | 0.4673 | 0.5009 | 0.5023 | 0.4971 | 0.5095 |
| ${{\varepsilon }_{N}},\% $ | 5.3 | 3.5 | 4.0 | 2.9 | 2.3 | 2.6 |
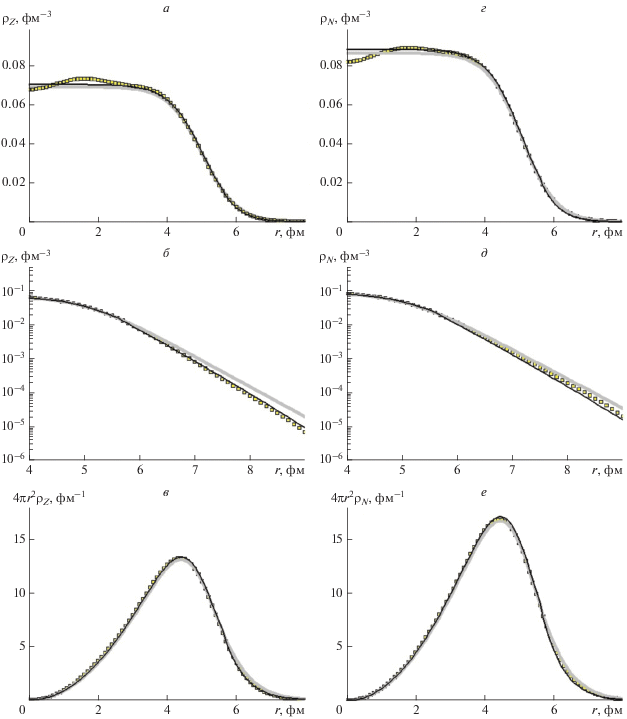
На рис. 1 и рис. 2 протонные и нейтронные плотности, полученные в результате аппроксимации фермиевской функцией (F-аппроксимации), сравниваются с плотностями, рассчитанными по методу HF SKX (HF SKX-плотностями). Согласие получается довольно хорошим; исключением является область, отдаленная от центра (область “хвостов” плотностей): здесь F-аппроксимация переоценивает HF SKX-плотности. Это неизбежно должно сказываться на величине энергии СиЯВ ${{U}_{n}}\left( R \right)$ сталкивающихся ядер (см. табл. 4).
Для улучшения результатов расчета в хвостовой области предложена модифицированная аппроксимация плотности экспоненциальной функцией при $r \geqslant {{r}_{E}} = {{R}_{Z}} + \Delta R$ ($r \geqslant {{r}_{E}}$ = ${{R}_{N}} + \Delta R$), в соответствии с которой диффузность ${{a}_{E}}$ убывает с расстоянием по следующему закону:
(6)
${{a}_{E}}\left( r \right) = a\left\{ {1 - \delta \cdot {{{\left( {r - {{r}_{E}}} \right)}}^{x}}} \right\}.$Соответственно, плотности имеют вид:
(7)
${{\rho }_{{FE}}}\left( r \right) = \left\{ {\begin{array}{*{20}{c}} {{{\rho }_{F}}\left( r \right),}&{r < {{r}_{E}}} \\ {{{\rho }_{F}}\left( {{{r}_{E}}} \right)exp\left[ {\frac{{{{r}_{E}} - r}}{{{{a}_{E}}\left( r \right)}}} \right],}&{r \geqslant {{r}_{E}}} \end{array}.} \right.$Аппроксимация плотностей ${{\rho }_{{ZSKX}}}\left( r \right),$ ${{\rho }_{{NSKX}}}\left( r \right)$ формулами (6), (7) показана на рис. 1 и 2. Теперь согласие с HF SKX-плотностями в хвостах намного лучше. Оно достигается ${\text{c}}$ параметрами δ = = 0.02 фм–x и ΔR = 0.5 фм для всех реперных ядер. Значения параметра $x$ оказываются одинаковыми для протонов и нейтронов для одного ядра, но различными для разных ядер (см. табл. 1). Следует отметить, что модифицированная аппроксимация (FE-аппроксимация) требует последующей дополнительной перенормировки: величины плотностей на малых расстояниях (плато) на рис. 1а, 1г и 2а, 2г не совпадают. Обозначим параметры, полученные в результате этой перенормировки, ${{\rho }_{{ZCFE}}}$ и ${{\rho }_{{NCFE}}}.$ Диффузности ${{a}_{Z}},$ ${{a}_{N}}$ и параметры ${{r}_{{Z0}}},$ ${{r}_{{N0}}}$ при этом не изменяются.
Значения параметров ${{\rho }_{{ZCFE}}},$ ${{a}_{Z}},$ ${{r}_{{Z0}}}$ (${{\rho }_{{NCFE}}},$ ${{a}_{N}},$ ${{r}_{{N0}}}$), полученные для реперных ядер, приведены в табл. 1. Обращает на себя внимание, что эти значения различны для протонов и нейтронов одного и того же ядра. Также в табл. 1 указаны относительные разности
(8)
${{\varepsilon }_{{Z\left( N \right)}}} = \frac{1}{Q}\sum\limits_{i = 1}^Q {\left| {1 - \frac{{{{\rho }_{{Z\left( N \right)FE}}}\left( {{{r}_{i}}} \right)}}{{{{\rho }_{{Z\left( N \right)SKX}}}\left( {{{r}_{i}}} \right)}}} \right|} ,$характеризующие степень согласия аппроксимирующей FE-плотности с аппроксимируемой HF SKX-плотностью.
Для нахождения нуклонных плотностей произвольных сферических ядер необходимо произвести линейную интерполяцию параметров ${{r}_{{Z0}}}$ (${{r}_{{N0}}}$), ${{a}_{Z}}$ (${{a}_{N}}$) по зарядовому числу ядра между соответствующими узловыми значениями, приведенными в табл. 1. После того как диффузности и параметры радиусов найдены, значения ${{\rho }_{{ZСFE}}}$ (${{\rho }_{{NСFE}}}$) определяются из условий нормировки.
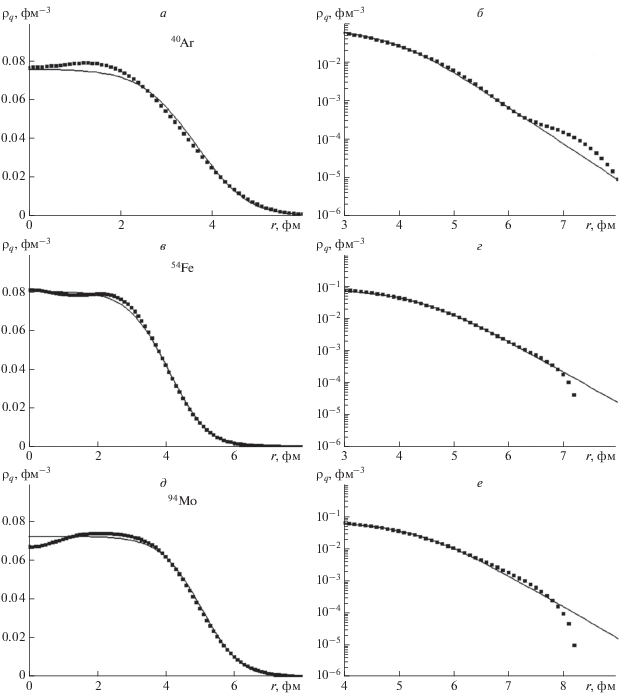
Рис. 3.
Зависимость зарядовой плотности ${{\rho }_{q}}\left( r \right)$ от расстояния от центра ядра для ядер 40Ar (а, б), 54Fe (в, г), 94Mo (д, е), в линейном (а, в, д) и логарифмическом (б, г, е) масштабах. Квадраты – экспериментальные данные [28], тонкие черные линии – результаты расчета с использованием протонных и нейтронных плотностей, полученных с помощью интерполяции по FE-алгоритму.
ЗАРЯДОВАЯ ПЛОТНОСТЬ В ЯДРАХ
Зарядовая плотность в сферическом ядре, ${{\rho }_{q}}\left( r \right),$ как функция расстояния $r$ от центра ядра вычисляется с помощью конволюции [42]
(9)
${{\rho }_{q}}\left( r \right) = \int {d{{{\vec {r}}}_{p}}{{\rho }_{Z}}\left( {{{r}_{p}}} \right){{f}_{p}}\left( {{{s}_{p}}} \right)} + \int {d{{{\vec {r}}}_{n}}{{\rho }_{N}}\left( {{{r}_{n}}} \right){{f}_{n}}\left( {{{s}_{n}}} \right)} .$Здесь ${{s}_{p}} = \left| {\vec {r} - {{{\vec {r}}}_{p}}} \right|,$ ${{s}_{n}} = \left| {\vec {r} - {{{\vec {r}}}_{n}}} \right|;$ ${{\vec {r}}_{p}}$ (${{\vec {r}}_{n}}$) означает радиус-вектор центра масс протона (нейтрона); ${{f}_{p}}\left( {{{s}_{p}}} \right)$ (${{f}_{n}}\left( {{{s}_{n}}} \right)$) – распределение заряда внутри протона (нейтрона).
Для распределения заряда внутри протона в настоящей работе используется гауссово распределение [42]
(10)
${{f}_{p}}\left( {{{s}_{p}}} \right) = \frac{1}{{{{\pi }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\sigma _{G}^{3}}}{\text{exp}}\left( {\frac{{ - s_{p}^{2}}}{{\sigma _{G}^{2}}}} \right),$Для зарядового распределения внутри нейтрона мы используем следующую аппроксимацию:
(11)
${{f}_{n}}\left( {{{s}_{n}}} \right) = \frac{{\left\langle {R_{n}^{2}} \right\rangle }}{{192\pi \sigma _{n}^{6}}}\left( {{{s}_{n}} - 3{{\sigma }_{n}}} \right){\text{exp}}\left( {\frac{{ - {{s}_{n}}}}{{{{\sigma }_{n}}}}} \right).$Здесь $\left\langle {R_{n}^{2}} \right\rangle = - 0.1149\,\,{\text{ф}}{{{\text{м}}}^{2}}$ – экспериментальное среднее значение квадрата зарядового радиуса нейтрона [29], а параметр ${{\sigma }_{n}} = 0.22\,\,{\text{фм}}{\text{.}}$
СРАВНЕНИЕ С ЭКСПЕРИМЕНТОМ
Зарядовые плотности ${{\rho }_{q}}\left( r \right),$ рассчитанные с помощью аппроксимированных протонных ${{\rho }_{Z}}\left( r \right)$ и нейтронных ${{\rho }_{N}}\left( r \right)$ плотностей, сравниваются с экспериментальными на рис. 3. При этих расчетах применен описанный выше FE-алгоритм, согласие получается довольно хорошим.
Количественное сравнение расчетных среднеквадратичных зарядовых радиусов ${{r}_{{msqFE}}}$ с экспериментальными ${{r}_{{msqexp}}}$ для нескольких сферических ядер, не являющихся реперными, проведено в табл. 2. Cравнение радиусов также удобно проиллюстрировать с помощью относительной разности
Таблица 2.
Среднеквадратичные зарядовые экспериментальные ${{r}_{{msqexp}}}$ [29] и расчетные ${{r}_{{msqFE}}}$ радиусы, их абсолютные $\Delta {{r}_{{msqexp}}}$ и относительные ${{\varepsilon }_{{exp}}}$ погрешности, а также относительные разности ${{\xi }_{{rmsq}}}$ (см. формулу (12)) для ряда изотопов
| Ядро | 58Ni | 116Sn | 112Sn | 40Ca | 50Ti | 90Zr | 96Zr |
|---|---|---|---|---|---|---|---|
| ${{r}_{{msqexp}}}$, фм | 3.7748 | 4.6266 | 4.5943 | 3.4764 | 3.5704 | 4.2696 | 4.3498 |
| $\Delta {{r}_{{msqexp}}}$, фм | 0.014 | 0.015 | 0.018 | 0.01 | 0.016 | 0.008 | 0.011 |
| ${{\varepsilon }_{{exp}}}$, % | 0.37 | 0.32 | 0.39 | 0.29 | 0.45 | 0.19 | 0.25 |
| ${{r}_{{msqFE}}}$, фм | 3.7757 | 4.6126 | 4.5656 | 3.4128 | 3.6055 | 4.3148 | 4.3128 |
| ${{{{\xi }}}_{{rmsq}}}$, % | 0.024 | –0.30 | –0.62 | –1.8 | 0.98 | 1.1 | –0.85 |
Из табл. 2 видно, что относительная разность между экспериментальными и расчетными среднеквадратичными зарядовыми радиусами не превышает 2%, а в большинстве случаев составляет менее 1%.
Применим теперь нуклонные плотности, полученные с помощью разработанного нами FE-алгоритма, для расчета энергии СиЯВ ${{U}_{n}}\left( R \right)$ (1) и кулоновских барьеров. В расчетах энергии СиЯВ использован эффективный нуклон-нуклонный потенциал ${{\nu }_{{NN}}}$ M3Y Paris с плотностной зависимостью CDM3Y1 (см. табл. 1 и формулу (6) в работе [43]). Кулоновская составляющая взаимодействия ядер вычислена также методом двойной свертки c потенциалом кулоновского отталкивания точечных зарядов (см. формулу (5) в [43]).
Результаты таких расчетов для ряда реакций представлены в табл. 3. В ней приведены следующие величины: высота расчетного барьера ${{U}_{{B0FE}}}$ для нулевого углового момента; высота экспериментального барьера ${{U}_{{B0exp}}}.$ Также указаны приближенные значения высот барьеров ${{B}_{Z}},$ определенные по оценочной формуле
(13)
${{B}_{Z}} = {{{{Z}_{P}}{{Z}_{T}}} \mathord{\left/ {\vphantom {{{{Z}_{P}}{{Z}_{T}}} {\left( {A_{P}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} + A_{T}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \right)}}} \right. \kern-0em} {\left( {A_{P}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}} + A_{T}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}} \right)}}\,\,{\text{МэВ}}.$Таблица 3.
Высоты кулоновских барьеров для рассматриваемых реакций: приближенная оценка ${{B}_{Z}}$ (см. формулу (13)); расчетное значение ${{U}_{{B0FE}}};$ экспериментальное значение ${{U}_{{B0exp}}};$ относительная разность ${{{{\xi }}}_{U}}$ (см. формулу (14))
| № пп | Реакция | ${{B}_{Z}}$, МэВ | ${{U}_{{B0FE}}}$, МэВ | ${{U}_{{B0exp}}}$, МэВ | Источник | ${{{{\xi }}}_{U}}$, % |
|---|---|---|---|---|---|---|
| 1 | 12C + 12С | 7.86 | 5.74 | 5.8 ± 0.3 | [44] | –1.0 |
| 2 | 12C + 16O | 9.98 | 7.48 | 7.7 ± 0.4 | [44] | –2.9 |
| 3 | 12C + 92Zr | 35.27 | 31.49 | 32.31 | [13] | –2.5 |
| 4 | 12C + 144Sm | 49.40 | 45.96 | – | – | – |
| 5 | 12C + 208Pb | 59.89 | 57.36 | 57.0 ± 0.4 | [45] | 0.63 |
| 6 | 12C + 204Pb | 60.17 | 57.74 | 57.55 | [13] | 0.33 |
| 7 | 16O + 58Ni | 35.05 | 30.73 | 31.67 | [13] | –3.0 |
| 8 | 16O + 92Zr | 45.49 | 41.21 | 41.96 | [13] | –1.8 |
| 9 | 16O + 116Sn | 54.08 | 50.02 | 50.96 | [13] | –1.8 |
| 10 | 16O + 112Sn | 54.49 | 50.43 | 51.02 | [13] | –1.2 |
| 11 | 16O + 144Sm | 63.91 | 60.23 | 61.03 | [13] | –1.3 |
| 12 | 16O + 208Pb | 77.68 | 75.23 | 74.52 | [13] | 0.95 |
| 13 | 16O + 204Pb | 78.03 | 75.30 | 74.9 | [46] | 0.53 |
| 14 | 36S + 208Pb | 142.19 | 143.15 | 140.4 ± 1.4 | [47] | 2.0 |
| 15 | 36S + 204Pb | 142.78 | 143.68 | 143.1 ± 0.2 | [48] | 0.41 |
| 16 | 36S + 144Sm | 116.11 | 114.59 | – | – | – |
| 17 | 40Ca + 50Ti | 61.94 | 57.56 | 58.21 | [13] | –1.1 |
| 18 | 36S + 90Zr | 82.23 | 78.34 | 77.97 | [13] | 0.47 |
| 19 | 36S + 96Zr | 81.21 | 77.68 | 75.61 | [13] | 2.7 |
| 20 | 40Ca + 90Zr | 101.25 | 97.91 | 96.88 | [13] | 1.1 |
| 21 | 40Ca + 96Zr | 100.01 | 97.08 | 94.59 | [13] | 2.6 |
Таблица 4.
Высота расчетного кулоновского барьера ${{U}_{{B0}}}$ для нулевого углового момента в ряде реакций для F- и FE-аппроксимаций в сравнении с высотами, вычисленными с HF SKX-плотностями
| № реакции в табл. 3 |
Реакция | Потенциал | Метод нахождения плотности | ${{U}_{{B0}}}$, МэВ | $\frac{{{{U}_{{B0SKX}}}}}{{{{U}_{{B0F\left( E \right)}}}}} - 1$, % |
|---|---|---|---|---|---|
| 3 | 12C + 92Zr | M3Y Paris | F | 31.13 | 2.14 |
| M3Y Paris | FE | 31.49 | 1.01 | ||
| M3Y Paris | HF SKX | 31.81 | |||
| 13 | 16O + 204Pb | M3Y Paris | F | 74.52 | 1.92 |
| M3Y Paris | FE | 75.30 | 0.89 | ||
| M3Y Paris | HF SKX | 75.98 | |||
| 11 | 16O + 144Sm | M3Y Paris | F | 59.56 | 1.86 |
| M3Y Paris | FE | 60.23 | 0.76 | ||
| M3Y Paris | HF SKX | 60.69 | |||
| M3Y Reid | F | 59.56 |
Относительная разность высот расчетного и экспериментального барьеров
не превышает 3%.
В табл. 4 приведены результаты расчетов ${{U}_{{B0}}}$ для трех реакций с учетом экспоненциального хвоста при аппроксимации плотностей и без него. Из этих результатов видно, что экспоненциальная поправка является значимой: высоты барьеров отличаются на 1.1%. Заметим, что при замене версии Paris потенциала нуклон-нуклонного взаимодействия M3Y на версию Reid высота барьера меняется менее чем на 0.017%.
ЗАКЛЮЧЕНИЕ
Зависимость плотности нуклонов в сферических ядрах от расстояния от центра ядра требуется для вычисления различных характеристик самих ядер и их взаимодействия. Расчет этих плотностей в микроскопических подходах весьма трудоемок. В литературе часто эти плотности аппроксимируют распределением Ферми. Однако при этом остается значительный произвол в параметрах этого профиля (радиус половинной плотности ${{r}_{0}}{{A}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}$ и диффузность $a$).
В настоящей работе мы аппроксимировали результаты расчетов нейтронных и протонных плотностей, полученных в микроскопическом подходе Хартри–Фока с SKX-параметрами, формулой Ферми для шести реперных ядер (F-аппроксимация, см. формулы (2), (3)). Проведенные расчеты показывают, что на периферии ядер (в хвостовой области) значения плотностей, полученные таким образом, существенно превышают плотности, вычисленные методом Хартри–Фока. Поэтому для этой области в настоящей работе предложена модернизированная экспоненциальная зависимость, использующая переменную диффузность. Такой FE-алгоритм позволил гораздо лучше воспроизвести микроскопические нуклонные плотности.
Далее был проведен расчет зарядовых плотностей в реперных ядрах с использованием нуклонных FE-плотностей. Оказалось, что рассчитанные таким образом зарядовые плотности хорошо согласуются с экспериментальными. Параметры распределения Ферми, ${{r}_{0}}$ и $a,$ для других сферических ядер находятся с помощью линейной интерполяции. В работе показано, что для многих сферических ядер предложенный подход обеспечивает отличие расчетного среднеквадратичного зарядового радиуса от экспериментального менее 2%.
Кроме того, разработанный FE-алгоритм применен для расчета высот кулоновских барьеров для ряда реакций. Расчетные величины высот оказались в хорошем согласии с экспериментальными. Отличие не превосходит 3%, а более чем в половине рассмотренных случаев укладывается и в 2%.
Разработанный алгоритм устраняет неопределенности в параметрах формулы Ферми для протонных и нейтронных плотностей и может быть полезен другим исследователям для быстрых и достаточно точных расчетов.
Список литературы
Berriman A.C., Hinde D.J., Dasgupta M. et al. // Nature. 2001. V. 413. P. 144.
Dasgupta M., Hinde D.J., Rowley N., Stefanini A.M. // Annu. Rev. Nucl. Part. Sci. 1998. V. 48. P. 401.
Кузякин Р.А., Саргсян В.В., Адамян Г.Г., Антоненко Н.В. // ЭЧАЯ. 2017. Т. 48. С. 21.
Hudan S., deSouza R.T., Umar A.S. et al. // Phys. Rev. C. 2020. V. 101. Art. No. 61601.
Montagnoli G., Stefanini A.M., Jiang C.L. et al. // Phys. Rev. C. 2020. V. 101. Art. No. 44608.
Fröbrich P., Gontchar I.I. // Phys. Rep. 1998. V. 292. P. 131.
Schunck N., Robledo L.M. // Reports Prog. Phys. 2016. V. 79. Art. No. 116301.
Usang M.D., Ivanyuk F.A., Ishizuka C., Chiba S. // Phys. Rev. C. 2017. V. 96. Art. No. 064617.
Schmitt C., Mazurek K., Nadtochy P.N. // Phys. Rev. C. 2019. V. 100. Art. No. 64606.
Hammerton K., Morrissey D.J., Kohley Z. et al. // Phys. Rev. C. 2019. V. 99. Art. No. 54621.
Oganessian Y.T., Utyonkov V.K. // Reports Prog. Phys. 2015. V. 78. Art. No. 36301.
Armbruster P., Münzenberg G. // Eur. Phys. J. H. 2012. V. 37. P. 237.
Newton J.O., Butt R.D., Dasgupta M. et al. // Phys. Rev. C. 2004. V. 70. Art. No. 024605.
Yilmaz B., Ayik S., Lacroix D., Yilmaz O. // Phys. Rev. C. 2014. V. 90. Art. No. 24613.
Maruhn J.A., Reinhard P.-G., Stevenson P.D., Strayer M.R. // Phys. Rev. C. 2006. V. 74. Art. No. 27601.
Benrabia K., Medjadi D.E., Imadalou M., Quentin P. // Phys. Rev. C. 2017. V. 96. Art. No. 34320.
Hagino K., Rowley N., Kruppa A.T. // Comp. Phys. Commun. 1999. V. 123. P. 143.
Загребаев В.И., Самарин В.В. // ЯФ. 2004. Т. 67. С. 1.
Jacobs P.M., Smilansky U. // Phys. Lett. B. 1983. V. 127. P. 313.
Chushnyakova M.V., Gontchar I.I. // J. Phys. G. 2013. V. 40. Art. No. 095108.
Chushnyakova M.V., Bhuyan M., Gontchar I.I., Khmyrova N.A. // Nucl. Phys. A. 2020. V. 994. Art. No. 121657.
Chushnyakova M.V., Gontchar I.I., Khmyrova N.A. // J. Phys. G. 2021. V. 48. Art. No. 015101.
Ismail M., Ramadan K.A. // J. Phys. G. 2000. V. 26. P. 1621.
Satchler G.R., Love W.G. // Phys. Rep. 1979. V. 55. P. 183.
Adamian G.G., Antonenko N.V., Jolos R.V. et al. // Int. J. Mod. Phys. E. 1996. V. 5. P. 191.
Khoa D.T. // Phys. Rev. C. 2001. V. 63. Art. № 034007.
Загребаев В.И., Карпов А.В., Аритомо Я. и др. // ЭЧАЯ. 2007. Т. 38. С. 893.
De Vries H., De Jager C.W., De Vries C. // Atom. Data Nucl. Data Tables. 1987. V. 36. P. 495.
Angeli I. // Atom. Data Nucl. Data Tables. 2004. V. 87. P. 185.
Cooper T., Bertozzi W., Heisenberg J. et al. // Phys. Rev. C. 1976. V. 13. P. 1083.
Sakaguchi H., Zenihiro J. // Prog. Part. Nucl. Phys. 2017. V. 97. P. 1
Terashima S., Sakaguchi H., Takeda H. et al. // Phys. Rev. C. 2008. V. 77. Art. No. 024317.
Miller Gerald A. // Phys. Rev. C. 2019. V. 100. Art. No. 044608.
Negele J.W. // Rev. Mod. Phys. 1982. V. 54. P. 913.
Gontchar I.I., Bhattacharya R., Chushnyakova M.V. // Phys. Rev. C. 2014. V. 89. Art. No. 034601.
Chushnyakova M.V., Bhattacharya R., Gontchar I.I. // Phys. Rev. C. 2014. V. 90. Art. No. 017603.
Bhattacharya R. // Nucl. Phys. A. 2013. V. 913. P. 1.
Bespalova O.V., Ermakova T.A., Klimochkina A.A., Spasskaya T.I. // Phys. Atom. Nucl. 2017. V. 80. P. 912.
Bespalova O.V., Fedorov N.A., Klimochkina A.A. et al. // Eur. Phys. J. A. 2018. V. 54. P. 2.
Chushnyakova M.V., Gontchar I.I. // Phys. Rev. C. 2013. V. 87. Art. No. 014614.
Gontchar I.I., Hinde D.J., Dasgupta M. et al. // Phys. Rev. C. 2006. V. 73. Art. No. 034610.
Łojewski Z., Nerlo-Pomorska B., Pomorski K., Dudek J. // Phys. Rev. C. 1995. V. 51. P. 601.
Gontchar I.I., Hinde D.J., Dasgupta M., Newton J.O. // Phys. Rev. C. 2004. V. 69. Art. No. 024610.
Kovar D.G., Geesaman D.F., Braid T.H. et al. // Phys. Rev. C. 1979. V. 20. P. 1305.
Mukherjee A., Hinde D.J., Dasgupta M. et al. // Phys. Rev. C. 2007. V. 75. Art. No. 044608.
Dasgupta M., Hinde D.J., Diaz-Torres A. et al. // Phys. Rev. Lett. 2007. V. 99. Art. No. 192701.
Yanez R., Loveland W., Vinodkumar A.M. et al. // Phys. Rev. C. 2010. V. 82. Art. No. 054615.
Hinde D.J., Dasgupta M., Herrald N. et al. // Phys. Rev. C. 2007. V. 75. Art. No. 054603.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая