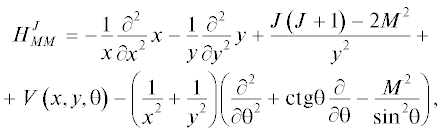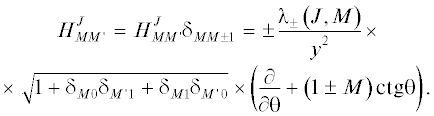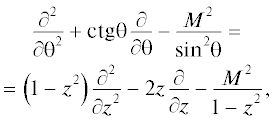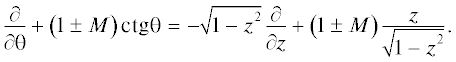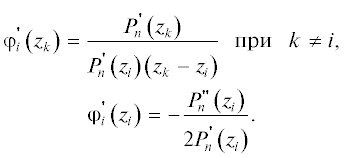1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 5, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 5, стр. 728-731

Метод представления дискретных переменных в исследовании слабосвязанных квантовых систем нескольких частиц с ненулевым орбитальным моментом

В. А. Тимошенко 1, *, Е. А. Яревский 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Санкт-Петербургский государственный университет”
Санкт-Петербург, Россия

* E-mail: vladimir.timoshenko7@mail.ru

Поступила в редакцию 20.11.2020
После доработки 28.12.2020
Принята к публикации 27.01.2021

Полный текст (PDF)

Аннотация

Решение квантовой задачи нескольких тел со слабым взаимодействием является сложной задачей и требует применения различных методов решения. В нашей работе был разработан и применен метод дискретных переменных, который позволяет значительно сократить время вычислений без потери точности.

ВВЕДЕНИЕ

В данной работе были рассмотрены системы частиц Ne3, He3, Li–He2, энергия связи которых мала, а волновая функция связанного состояния значительно распространена в пространстве. Такие системы представляют большой интерес и активно исследовались, в частности, в работах [1–7]. Так как для данных молекул потенциал межатомного взаимодействия слабый, задача по нахождению энергий связи и волновых функций оказывается весьма сложной. При малых изменениях входных параметров (например, потенциалов) или при высокой погрешности вычислений результат может сильно отличаться от правильного. Для получения точных результатов необходимы значительные вычислительные ресурсы и применение разнообразных подходов и методов решения задачи.

Целью данной работы является разработка и реализация метода дискретных переменных (discrete variable representation или DVR) [7] и его применение для расчета слабосвязанных молекулярных систем. Применение данного метода позволяет выполнять расчеты с меньшими вычислительными затратами и сократить время вычислений без потери точности. Благодаря свойствам DVR-функций определение матричных элементов оператора потенциальной энергии значительно упрощается.

Изначально метод был разработан для квантовой задачи трех тел с нулевым орбитальным моментом [8]. DVR-разложение было построено по полиномам Лежандра. В данной работе алгоритм был обобщен на случай ненулевого орбитального момента. Также были исследованы особенности DVR-разложения по полиномам Якоби и по присоединенным полиномам Лежандра.

Разработанный алгоритм был применен для вычисления энергий связи систем Ne3, He3, Li–He2. Проведено сравнение результатов с результатами других авторов [2–4].

МЕТОД ДИСКРЕТНЫХ ПЕРЕМЕННЫХ ДЛЯ НЕНУЛЕВОГО ОРБИТАЛЬНОГО МОМЕНТА

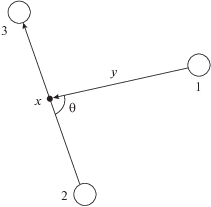
Для представления Гамильтониана квантовой системы трех тел были выбраны координаты Якоби (рис. 1). Переменная x обозначает расстояние между частицами 2 и 3, y – расстояние между частицей 1 и центром масс пары (23), θ – угол между векторами $\vec {x}$ и $\vec {y}.$ Используя разложение волновой функции по D-функциям Вигнера [9], можно записать для ненулевого орбитального момента J и его проекции M гамильтониан системы трех частиц, который состоит из диагональных и внедиагональных блоков [10]:

(1)
(2)
Рис. 1.

Координаты Якоби для системы трех тел.

Каждый блок этого матричного гамильтониана действует на компоненту блочного вектора волновой функции, отвечающую проекции M'. Потенциал V = V(x, y, θ) в (1) – сумма парных потенциалов, каждый из которых зависит только от расстояния между частицами, и ${{{{\lambda }}}_{ \pm }}\left( {J,M} \right)$ = = $\sqrt {J\left( {J + 1} \right) - M\left( {M \pm 1} \right)} .$

Перепишем оператор кинетической энергии для координаты z = cosθ и применим для нее метод DVR. Для диагональных и внедиагональных частей, содержащих угловую переменную:

(3)
(4)

DVR-функции φi(z) и их производные $\varphi _{i}^{'}\left( z \right)$ построены при помощи ортогональных полиномов Pn(z) и соответствующей квадратурной формулы Гаусса. Свойства DVR-функции позволяют упростить вычисления потенциальной энергии.

(5)
${{{{\varphi }}}_{i}}\left( {{{z}_{k}}} \right) = \frac{{{{P}_{n}}\left( {{{z}_{k}}} \right)}}{{P_{n}^{'}\left( {{{z}_{i}}} \right)\left( {{{z}_{k}} - {{z}_{i}}} \right)}},\,\,\,\,{{{{\varphi }}}_{i}}\left( {{{z}_{k}}} \right) = {{{{\delta }}}_{{ik}}}.$

Здесь точки z1, …, zn – нули полинома Pn(z).

Для вычисления матричных элементов оператора кинетической энергии необходимо определить производные $\varphi _{i}^{'}\left( z \right).$ Раскладывая Pn(z) в ряд Тейлора в точках zi и подставляя в выражение (5), получаем:

(6)

Полиномы Якоби

Интеграл на отрезке [–1; 1] может быть аппроксимирован при помощи квадратурной формулы Гаусса–Якоби [11]:

(7)
$\int\limits_{ - 1}^1 {f\left( z \right)dz} \approx \sum\limits_{i = 1}^n {\frac{{{{w}_{i}}}}{{{{\rho }}\left( {{{z}_{i}}} \right)}}} f\left( {{{z}_{i}}} \right),$
где ρ = (1 – z)α(1 + z)β – весовая функция, z1, …, zn – нули полинома $P_{n}^{{({{\alpha }},{{\beta }})}}(z).$

Выбирая в качестве базисных DVR-функции и вычисляя матричные элементы потенциальной энергии с помощью квадратурной формулы Гаусса–Якоби, получим диагональную матрицу оператора потенциальной энергии в DVR-представлении:

(8)
$\begin{gathered} {{V}_{{ij}}} = \int\limits_{ - 1}^1 {\frac{{{{{{\varphi }}}_{i}}\left( z \right)}}{{\sqrt {{{w}_{i}}} }}} V\left( {x,y,z} \right)\frac{{{{{{\varphi }}}_{j}}\left( z \right)}}{{\sqrt {{{w}_{j}}} }}dz \approx \\ \approx \sum\limits_k {\frac{{{{w}_{k}}}}{{{{\rho }}\left( {{{z}_{k}}} \right)}}} V\left( {x,y,{{z}_{k}}} \right)\frac{{{{{{\varphi }}}_{i}}\left( {{{z}_{k}}} \right)}}{{\sqrt {{{w}_{i}}} }}\frac{{{{{{\varphi }}}_{j}}\left( {{{z}_{k}}} \right)}}{{\sqrt {{{w}_{j}}} }} = \frac{{V\left( {x,y,{{z}_{i}}} \right)}}{{{{\rho }}\left( {{{z}_{i}}} \right)}}{{\delta }_{{ij}}}. \\ \end{gathered} $

Используя свойства полиномов Якоби, можно выписать значения производных $\varphi _{i}^{'}(z)$ явным образом:

(9)
${{\varphi }}_{i}^{'}\left( {{{z}_{i}}} \right) = \frac{{{{\beta }} - {{\alpha }} - \left( {{{\alpha }} + {{\beta }} + 2} \right){{z}_{i}}}}{{2\left( {1 - z_{i}^{2}} \right)}}.$

Присоединенные полиномы Лежандра

Присоединенные полиномы Лежандра $P_{n}^{{(m,m)}}(z)$ содержат множитель sinmθ, явный учет которого может привести к меньшим погрешностям при вычислениях. Эти полиномы могут быть выражены через полиномы Якоби:

(10)
$P_{{n + m}}^{m}\left( z \right) = {{\left( { - 1} \right)}^{m}}\frac{{\left( {n + 2m} \right)!}}{{{{2}^{m}}\left( {n + m} \right)!}}{{\left( {1 - {{z}^{2}}} \right)}^{{{m \mathord{\left/ {\vphantom {m 2}} \right. \kern-0em} 2}}}}P_{n}^{{\left( {m,m} \right)}}\left( z \right).$

Нули полиномов $P_{{n + m}}^{m}(z),$ отличные от ±1, совпадают с нулями полиномов $P_{n}^{{(m,m)}}(z).$ Таким образом, DVR-функции, построенные по присоединенным полиномам Лежандра:

(11)
$\begin{gathered} {{{{\varphi }}}_{i}}\left( z \right) = \frac{{P_{{n + m}}^{m}\left( z \right)}}{{P_{{n + m}}^{{m'}}\left( {{{z}_{i}}} \right)\left( {z - {{z}_{i}}} \right)}} = \\ = \,\,{{\left( {\frac{{1 - {{z}^{2}}}}{{1 - z_{i}^{2}}}} \right)}^{{\frac{m}{2}}}}\frac{{P_{n}^{{\left( {m,m} \right)}}\left( z \right)}}{{P_{n}^{{\left( {m,m} \right)'}}\left( {{{z}_{i}}} \right)\left( {z - {{z}_{i}}} \right)}}. \\ \end{gathered} $

Используя свойства присоединенных полиномов Лежандра, можно найти простое выражение для значений производных DVR-функций в узлах:

(12)
${{\varphi }}_{i}^{'}\left( {{{z}_{i}}} \right) = - \frac{{{{z}_{i}}}}{{1 - z_{i}^{2}}}.$

РЕЗУЛЬТАТЫ

В ходе исследования был разработан алгоритм, объединяющий метод конечных элементов [5] для координат x и y и метод дискретных переменных для угловой координаты z. При помощи реализованного алгоритма были вычислены энергии связи квантово-механических систем трех частиц. Энергетические уровни слабосвязанных молекул 6Li–He2 и 7Li–He2 были посчитаны с применением DVR-метода, построенного по полиномам Лежандра. Благодаря использованию DVR-разложения удалось значительно сократить время вычисления без потери точности. Полученные энергии связи, время вычислений и относительные ошибки для системы He3 представлены в табл. 1. Можно увидеть, что сходимость вычислений без применения DVR имеет вариационный характер, в то время как результаты с DVR приближаются к точному значению снизу. Энергии обоих методов сходятся к одному значению при увеличении количества полиномов в разложении.

Таблица 1.  

Энергии связи He3, относительные погрешности и время интегрирования при различном количестве функций в разложении

n 10 20 30 40
Разложение по полиномам Лежандра
E, см–1 –3.13 · 10−3 –7.05 · 10−2 –7.99 · 10−2 –8.18 · 10−2
δE 9.62 · 10−1 1.42 · 10−1 2.80 · 10−2 5.34 · 10−3
t, c 12.3 84.4 277.9 662.9
Метод представления дискретных переменных
E, см–1 –1.29 · 10−2 –9.72 · 10−2 –8.35 · 10−2 –8.26 · 10−2
δE 5.69 · 10−1 1.81 · 10−1 1.59 · 10−2 4.21 · 10−3
t, c 2.4 9.5 21.6 40.0
Коэффициент ускорения
  5.1 8.9 12.9 16.6

Вычисленные значения энергий связи систем 6Li–He2 и 7Li–He2 приведены в табл. 2. Для сравнения приведены также результаты других авторов [2–4] с советующими потенциалами [12–14] взаимодействия между частицами He–He и He–Li. В случае потенциалов TTY + KTTY и LM2M2 + KTTY полученные нами энергетические уровни находятся глубже. В силу того, что используемый подход к решению задачи близок к вариационному, можно считать, что полученные нами результаты ближе к истинным значениям.

Таблица 2.  

Энергия связи системы Li–He2 в см–1 для потенциалов TTY [12], LM2M2 [13], Cvetko [14]

  He–He pot. Li–He pot. 6Li–He2 7Li–He2
J. Yuan, C.D. Lin [2] TTY KTTY –2.18 · 10−2 –3.18 · 10−2
Данная работа TTY KTTY –3.71 · 10−2 –5.41 · 10−2
I. Baccarelli et al. [3] LM2M2 Cvetko –3.61 · 10−2 –5.10 · 10−2
Данная работа LM2M2 Cvetko –2.62 · 10−2 –4.07 · 10−2
E.A. Kolganova [4] LM2M2 KTTY –2.46 · 10−2 –3.54 · 10−2
Данная работа LM2M2 KTTY –3.71 · 10−2 –5.41 · 10−2

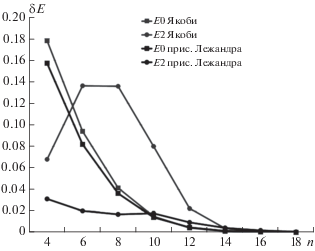
На следующем этапе работы был реализован метод с построением DVR-функций по полиномам Якоби $P_{n}^{{({{\alpha }},{{\beta }})}}(z)$ и присоединенным полиномам Лежандра $P_{{n + m}}^{m}(z).$ Использование данных полиномов позволяет выбирать параметры α, β и m таким образом, что весовая функция ρ(z) сглаживает особенность потенциала. Данный подход был реализован и протестирован на задаче по нахождению энергий связи тримера неона для орбитального момента J = 1 и положительной симметрии. График зависимости погрешности в зависимости от количества DVR-функций приведен на рис. 2. Результаты показывают, что применение присоединенных полиномов Лежандра улучшает сходимость алгоритма в сравнении с полиномами Якоби.

Рис. 2.

График сходимости значений двух энергетических уровней Ne3 для DVR-функций, построенных по полиномам Якоби и присоединенным полиномам Лежандра.

ЗАКЛЮЧЕНИЕ

Подход, сочетающий метод дискретных переменных и конечных элементов, был применен для решения квантовой задачи трех тел. Рассчитаны энергетические уровни слабосвязанных систем, состоящих из нескольких атомов. Благодаря применению метода DVR время расчетов было значительно сокращено без потери точности.

Метод DVR был расширен за счет использования различных типов квадратурных формул для построения DVR-функций, в частности, формул, основанных на полиномах Якоби и присоединенных полиномах Лежандра. Такие формулы позволяют более точно учесть особенности парных потенциалов на малых расстояниях.

Следующим шагом исследований является обобщение предложенного метода на комплекснозначные функции, что позволит повысить эффективность поиска резонансных состояний и исследований процессов рассеяния.

Исследование выполнено при финансовой поддержке РФФИ (проект № 19-32-90148). Расчеты выполнены в Вычислительном Центре СПбГУ.

Список литературы

  1. Motovilov A., Sandhas W., Sofianos S., Kolganova E. // Eur. Phys. J. D. 2001. V. 13. P. 34.

  2. Yuan J., Lin C.D. // J. Phys. B. 1998. V. 31. P. 647.

  3. Baccarelli I., Delgado-Barrio G., Gianturco F.A. et al. // Phys. Chem. Chem. Phys. 2000. V. 2. P. 4067.

  4. Kolganova E. // Few-Body Syst. 2017. V. 58. P. 57.

  5. Salci M., Levin S.B., Elander N., Yarevsky E.A. // J. Chem. Phys. 2008. V. 129. Art. No. 134304.

  6. Esry B.D., Lin C.D., Greene C.H. // Phys. Rev. A. 1996. V. 54. P. 394.

  7. Light J.C., Tucker C. Jr. // Adv. Chem. Phys. 2000. V. 114. P. 263.

  8. Timoshenko V., Yarevsky E. // Springer Proc. Phys. 2020. V. 238. P. 57.

  9. Варшалович Д.А., Москалев А.Н., Херсонский В. Квантовая теория углового момента. Л.: Наука, 1975.

  10. Elander N., Levin S.B., Yarevsky E. // Int. J. Quant. Chem. 2009. V. 109. No. 3. P. 459.

  11. Abramowitz M., Stegun I.A. Handbook of mathematical functions with formulas, graphs, and mathematical tables. N.Y.: Dover, 1964.

  12. Tang K., Toennies J., Yiu C. // Phys. Rev. Lett. 1995. V. 74. P. 1546.

  13. Aziz R., Slaman M. // J. Chem. Phys. 1991. V. 84. Art. No. 8047.

  14. Cvetko D., Lausi A., Morgante A., Tommasini F. // J. Chem. Phys. 1994. V. 100. Art. No. 2052.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал