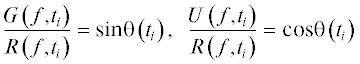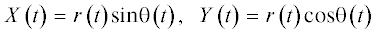Известия РАН. Серия физическая, 2021, T. 85, № 6, стр. 907-912

Эксперимент проводился в акватории глубиной $H\sim 87$ м и скоростью звука $c\sim 1470$ м/с [1]. Прием акустических сигналов осуществлялся на одиночный векторно-скалярный приемник (ВСП) вертикальной антенны, расположенного на глубине ${{z}_{q}} = 30$ м. Интерферограмма (квадрат модуля давления) движущегося шумового источника регистрировалась в полосе $\Delta f = 115$ кГц. Длительность принимаемой шумовой реализации ${{\delta }}t = 0.2$ с. Входное отношение сигнал/помеха (по мощности) $q\sim 8$ (9 дБ). Априорная информация о гидрофизических характеристиках акватории отсутствовала. Цель работы заключалась в проверке работоспособности интерферометрического метода локализации шумового источника в высокочастотной области.

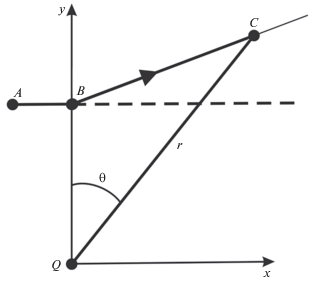
Схема движения источника относительно расположения ВСП в окрестности траверса показана на рис. 1 (вид сверху). Оси x и y ВСП Q совпадают с положительными направлениями системы координат. Из начальной точки A источник приближался к приемнику, проходил точку B траверса и далее удалялся по направлению к точке C. После прохождения точки C источник совершал петлеобразные траектории (на рис. 1 они не отображены). Горизонтальное расстояние источника до антенны обозначено r, пеленг – θ.

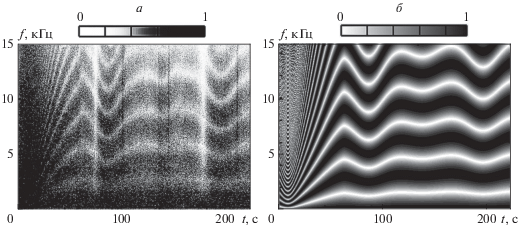
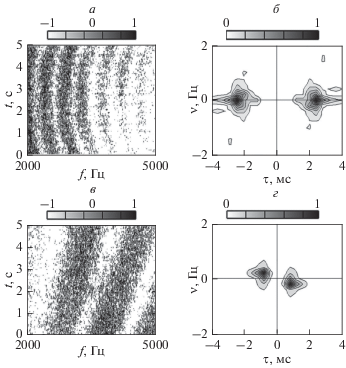
На рис. 2 приведены экспериментальная ${{I}_{e}}\left( {f,~t} \right)$ (а) и модельная ${{I}_{m}}\left( {f,~t} \right)$ (б) интерферограммы. В момент времени $~t = 10$ с прохождения точки траверса частотный масштаб изменчивости оценивается как $\Lambda = 404$ Гц (рис. 2а). При удалении от точки траверса частотный масштаб возрастает, что приводит к увеличению ширины интерференционной полосы. При этом он практически не зависит от частоты. Временной масштаб D изменчивости интерферограммы с возрастанием частоты уменьшается и увеличивается с возрастанием времени наблюдения. В точке траверса, например, на частоте $f = 3.5$ кГц − $D = 2.9$ с. Крутизна интерференционных полос в области траверса возрастает со временем и частотой, и по мере удаления от нее уменьшается. Данные закономерности характерны до момента времени $t{\kern 1pt} '\sim 70$ с, т.е. по истечении 60 с после прохождения точки траверса. Для значений $t > t{\kern 1pt} '$ интерферограмма приобретает осциллирующий характер, вызванный многократным изменением направления движения (см. рис. 4в).

Модельная интерферограмма I_m(f, t) (рис. 2б), адекватно передающая основные свойства экспериментальной интерферограммы, строилась на основе интерференции полей двух лучей с использованием лучевой программы. При этом предполагалось, что в течение временного интервала $\Delta t = 20$ c источник двигался по прямолинейной траектории.

Спектральные плотности на выходе двукратного преобразования Фурье интерферограммы ${{I}_{e}}\left( {f,~t} \right)$ (назовем условно голограммой) для двух моментов времени ${{t}_{i}} = 10,50$ с представлены на рис. 3. С целью повышения контрастности и информативности на интерферограммах вырезаны средние значения. Изображение источника локализовано в форме двух фокальных пятен, зеркально перевернутых относительно начала координат. Одно из них, лежащее во втором и третьем квадратах, можно рассматривать как мнимое изображение источника, второе, лежащее в первом и четвертом квадрантах, − как действительное изображение. Число фокальных пятен определяет число лучей, формирующих интерферограмму: каждое фокальное пятно обусловлено интерференцией двух лучей. В эксперименте интерферограмма на всей траектории формировалась двумя лучами: прямым лучом и лучом, отраженным от верхней границы $z = 0.$ Координаты положений максимумов фокальных пятен: ${{\tau }} = 2.4$ мс, ν = 0 Гц, ${{t}_{i}} = 10$ с; τ = 0.9 мс, ν = –0.2 Гц, t_i = 50 с. Этим моментам времени соответствуют частотные масштабы Λ = = 404 Гц; $\Lambda = 2.5$ кГц (см. рис. 2а).

Направление на источник реализовывалось применением интерферометрического метода пеленгования, основанного на отношении очищенных от помех интерферограмм

в фиксированные моменты времени ${{t}_{i}},$ где $R = {{V}_{r}},$ $G = {{V}_{x}},$ $U = {{V}_{y}}$ [2]. Здесь ${{V}_{{x,~y}}}$ – горизонтальные компоненты колебательной скорости ${{V}_{r}} = \sqrt {V_{x}^{2} + V_{y}^{2}} .$ При обработке очищение интерферограмм от помехи не проводилось, так как входное отношение сигнал/помеха было достаточным для отчетливого наблюдения полос.

Горизонтальное расстояние до приемника r, глубина z и скорость w источника оценивались как координаты основного максимума трехмерной взаимокорреляционной функции экспериментальной ${{I}_{e}}$ и модельной ${{I}_{m}}$ интерферограмм

т.е. $E\left( {r,~z,~w} \right) = {\text{max}}E\left( {{{r}_{*}},~{{z}_{*}},~{{w}_{*}}} \right).$ Варьируемые величины обозначены нижним индексом звездочка (*), а верхний индекс звездочка “*” означает комплексное сопряжение. При обработке (2) априори считалось, что источник расположен на глубине $1~\,\, \leqslant z \leqslant 70\,{\text{м}},$ от ВСП удален на расстояние $50\,{\text{м}} \leqslant r \leqslant 3\,{\text{км}},$ скорость $2 \leqslant w \leqslant 35\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}.$ Перебор параметров проводился с шагом: расстояние − ${{\delta }}r = 25$ м, глубина − ${{\delta }}z = 0.5$ м, скорость − δw = = 1 м/с. Шаг дискретизации по частоте δf = 0.5 Гц, по времени ${{\delta }}t = 2$ с. Обработка проводилась во временном интервале $\Delta t = 20$ c и полосе Δf = 1–15 кГц.

Для отслеживания временного восстановления параметров источника использовалось каскадное вычисление взаимокорреляционной функции. В начальный момент времени ${{t}_{0}} = 0$ осуществлялась обработка (2) во временном интервале $\Delta t = 20$ с. В момент времени 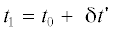проводилась следующая обработка в течение времени $\Delta t,$ ${{\delta }}t{\kern 1pt} ' = 5$ с, и т.д. За время наблюдения $T = 275$ с получено $N = \left[ {{{\left( {T - \Delta t} \right)} \mathord{\left/ {\vphantom {{\left( {T - \Delta t} \right)} {{{\delta }}t{\kern 1pt} '}}} \right. \kern-0em} {{{\delta }}t{\kern 1pt} '}}} \right] + 1 = 52$ отсчета параметров источника.

Восстановленные временные зависимости параметров источника продемонстрированы на рис. 4.

На рис. 4а экспериментальная зависимость пеленга от времени ${{\theta }}\left( t \right)$ изображена сплошной линией, пунктиром – модельная зависимость в предположении движения источника вдоль прямой, параллельной оси x (см. рис. 1, пунктир). Мелкомасштабные осцилляции обусловлены колебаниями приемной системы в вертикальной плоскости, крупномасштабные осцилляции – петлеобразными траекториями источника. Для пеленгования источника знаний о гидрофизических характеристиках акватории не требуется.

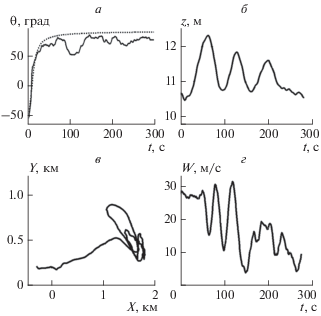
На рис. 4б показана зависимость z(t). Как видно, во время эксперимента глубина источника изменялась в пределах ~1.5 м и в среднем оценивается как $z = 11.4$ м. Осцилляции глубины приходятся на времена, когда источник совершал петлеобразные траектории.

По данным ${{\theta }}\left( t \right)$ и $r\left( t \right)$ оценены координаты источника

и реконструирована траекторная зависимость $Y\left( X \right),$ которая представлена на рис. 4в. Из нее следует, что точка траверса была удалена от ВСП на расстояние $r = 188$ м. После прохождения точки траверса источник перемещался по прямой, не параллельной оси x и в момент времени $t{\kern 1pt} '\sim 70$ с начинал совершать петлеобразные траектории.

Скорость источника w на временном интервале $\Delta t$ определялась как

Временная зависимость $w\left( t \right)$ отображена на рис. 4г. Для кривой $w\left( t \right)$ характерны две временные области. Первая область, $0 \leqslant t \leqslant 58$ с, где источник двигался преимущественно по прямолинейной траектории практически с постоянной скоростью $w = 27.4$ м/с. Вторая область, $58 < t \leqslant 275$ с, когда источник двигался по петлеобразным траекториям, скорость имеет сложный изрезанный характер. С уменьшением размера петли скорость снижалась.

Рассмотрим связь характеристик интерферограммы (или положения максимумов фокальных пятен голограммы) с параметрами движущегося источника. Обсудим это на простом примере удаления источника от точки траверса B по прямолинейной траектории параллельно оси x с постоянной скоростью w и на фиксированной глубине z (рис. 1, пунктир). Допустим, что коэффициент отражения от свободной поверхности не зависит от частоты, угла падения и равен –1. Источник начинал движение из точки траверса в сторону удаления от приемника. Тогда двухлучевая интерферограмма принимает вид [3]

где фаза Здесь $\eta = {{2{{z}_{q}}z} \mathord{\left/ {\vphantom {{2{{z}_{q}}z} c}} \right. \kern-0em} c},$ c – скорость звука, ${{z}_{q}}$ – глубина приемника; $~r\left( t \right) = \sqrt {r_{0}^{2} + {{{\left( {wt} \right)}}^{2}}} $ – горизонтальное расстояние от приемника до источника в момент времени t,$~{{r}_{0}}$ – расстояние в начальный момент времени $t = 0$ от точки траверса до приемника; $\bar {R}\left( t \right) = \sqrt {{{r}^{2}}\left( t \right) + z_{q}^{2}} ;$ ${{B}^{2}}$ – коэффициент, характеризующий мощность излучения. Принимая в среднем глубину источника $z = 11$ м, имеем $\eta = 0.47$ м ⋅ с.

Кривая интерференционных максимумов определяется условием

Используя (6), из (7) для производной кривой постоянной фазы получаем

Отсюда следует, что крутизна интерференционных полос в области траверса возрастает со временем, частотой и скоростью источника, и по мере удаления от точки траверса уменьшается. Подобный результат зарегистрирован в эксперименте. Решая дифференциальное уравнение (8) при начальном условии $f\left( 0 \right) = {{f}_{0}},$ находим уравнение кривой интерференционных максимумов поля источника

Частотный масштаб изменчивости интерферограммы в момент времени t, как следует из (6), равен

так что он возрастает с увеличением скорости источника и удалением от приемника, уменьшается с увеличением заглубления и не зависит от частоты. Подобные закономерности в зависимости от расстояния и частоты наблюдались в эксперименте. Например, в точке траверса (${{r}_{0}} = 189$ м) получаем $\Lambda \left( 0 \right) = 402$ Гц, что согласуется с экспериментальным значением $\Lambda = 404$ Гц. Если ширину интерференционной полосы $\Delta f\left( t \right)$ определить как ширину, в пределах которой фаза (6) меняется на ${{\pi /}}2,$ то $\Delta f\left( t \right) = {{\Lambda \left( t \right)} \mathord{\left/ {\vphantom {{\Lambda \left( t \right)} 4}} \right. \kern-0em} 4}.$ Величина $\Delta {{\tau ,}}$ обратная частотному масштабу, $\Delta {{\tau }} = {1 \mathord{\left/ {\vphantom {1 \Lambda }} \right. \kern-0em} \Lambda },$ представляет собой разность времен прихода прямого и отраженного лучей.

Временной масштаб D изменчивости интерферограммы, как следует из (6), определяется условием

Аналитического решения эта задача не имеет, поэтому обратимся к тем результатам, которые можно извлечь из (11) в некоторых предельных случаях.

1. Пусть $r_{0}^{2} \gg {{\left( {wt} \right)}^{2}},$ т.е. рассматривается окрестность точки траверса. Тогда, как следует из (11),

где $a = {{2r_{0}^{3}} \mathord{\left/ {\vphantom {{2r_{0}^{3}} {f{{w}^{2}}}}} \right. \kern-0em} {f{{w}^{2}}}}.$ На практике можно ограничиться более слабым неравенством $r_{0}^{2} \geqslant 3{{\left( {wt} \right)}^{2}}.$ Для условий эксперимента данное приближение реализуется при $t \leqslant 4$ с. В точке траверса $t = 0$ имеем

Для полученных оценок (${{r}_{0}} = 189$ м, $\eta = 0.47$ м · с, $w = 27.4$ м/с), задаваясь частотой $f = 3.5$ кГц, имеем $D\left( 0 \right) = 3.3$ с, что близко к экспериментальному значению $D = 2.9$ с.

2. Пусть $r_{0}^{2} \ll {{\left( {wt} \right)}^{2}},$ т.е. расстояние от источника до приемника больше по сравнению с траверсным расстоянием. В этом случае, согласно (11),

где $b = {w \mathord{\left/ {\vphantom {w f}} \right. \kern-0em} f}.$ С ростом времени слагаемое $bt$ растет и при значении ${{t}_{{cr}}} = {1 \mathord{\left/ {\vphantom {1 b}} \right. \kern-0em} b}$ временной масштаб становится бесконечным. Это означает локализацию интерференционных полос вдоль горизонтальных линий. Предельному значению ${{t}_{{cr}}}$ отвечает удаление источника от приемника ${{r}_{{cr}}} = \eta f.$ Задаваясь значениями $\eta = 0.47$ м ⋅ с, $f = 3.5$ кГц, получаем: ${{t}_{{cr}}} = 60$ с, ${{r}_{{cr}}} = 1.64$ км. Данный эффект наблюдается на экспериментальной и модельной интерферограммах (рис. 2).

Очевидным условием наблюдаемости интерферограммы является требование, чтобы ширина спектра $\Delta f$ хотя бы в несколько раз превышала частотный масштаб $\Lambda \left( t \right)$ (10). В качестве критерия наблюдаемости интерферограммы примем неравенство

которое эквивалентно условию, что наблюдается одна и более интерференционных полос. Ширина спектра ограничивает удаление источника от приемника, при этом максимальное удаление, соответствующее условию реализации одной полосы, оценивается как

так что с увеличением полосы анализа и заглубления источника максимальное удаление возрастает. Для условий эксперимента ${{r}_{{{\text{max}}}}} = 3.29$ км.

Координаты максимума фокального пятна голограммы (1), отвечающие действительному изображению источника, в точке траверса, как можно показать, равны ${{\tau }} = {\eta \mathord{\left/ {\vphantom {\eta {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}},$ $\nu = 0.$ Для оценок $\eta = 0.47$ м ⋅ с, ${{r}_{0}} = 189$ м получаем ${{\tau }} = 2.5$ мс, что близко экспериментальному значению τ = 2.4 мс (см. рис. 3).

Как показал проведенный анализ, модельная интерферограмма адекватно передает основные свойства экспериментальной интерферограммы до момента времени, когда источник начал совершать петлеобразные траектории.

Таким образом, изложен высокочастотный интерферометрический метод локализации шумового источника, использующий сигнал с одного из одиночных ВСП антенны. В основе метода лежит частотно-временная обработка шумовых сигналов, согласованная с интерферограммой, формируемой движущимся источником. Модельная интерферограмма строилась на основе интерференции полей двух лучей: прямого и отраженного от свободной поверхности лучей. Метод апробирован на данных натурного эксперимента. По результатам обработки восстановлены временные зависимости пеленга, расстояния до приемника, скорости и глубины источника.

Двухлучевая модельная интерферограмма не требует знаний о параметрах дна и устойчива к поверхностному волнению. Поэтому предложенная согласованная обработка оказалась работоспособной, позволив получить правильные временные зависимости параметров шумового источника. Совокупная картина фокальных пятен голограммы позволяет определить число лучей, формирующих поле, в различных областях пространства. С удалением источника от приемника число лучей может увеличиваться, что будет приводить к усложнению интерференционной картины волнового поля. Если фокальные пятна не перекрываются, то на голограмме можно вырезать отдельные фокальные пятна и по отношению к ним реализовать обратное двукратное преобразование Фурье. Это даст возможность работать с двухлучевой интерферограммой, устойчивой по отношению к вариациям параметров дна.

Работа выполнена при финансовой поддержке РФФИ (проекты № 19-08-00941 и 19-29-06075).