Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 53-57
Ионизация примесей статическим и переменным электрическими полями в однослойных углеродных нанотрубках полупроводникового типа
О. Ю. Бабина 1, С. Ю. Глазов 1, 2, *, И. А. Подгорная 1, 2
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Волгоградский государственный социально-педагогический университет”
Волгоград, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Волгоградский государственный медицинский университет”
Волгоград, Россия
* E-mail: ser-glazov@yandex.ru
Поступила в редакцию 24.08.2021
После доработки 06.09.2021
Принята к публикации 22.09.2021
- EDN: HYVVKE
- DOI: 10.31857/S0367676522010033
Аннотация
Исследована вероятность ионизации примесей в однослойных углеродных нанотрубках полупроводникового типа в присутствии сильных постоянного и переменного электрических полей в квазиклассическом приближении. Электрические поля поляризованы вдоль оси нанотрубки. Получены аналитические выражения для вероятности ионизации в присутствии только постоянного или переменного электрических полей в предельных случаях.
ВВЕДЕНИЕ
Электрические свойства углеродных нанотрубок (УНТ) существенно различаются в зависимости от их структуры, условий синтеза, наличия примесей и дефектов. Первоначальные эксперименты проводились над образцами, содержащими хаотично расположенные нанотрубки разных типов, что затрудняло теоретическое описание полученных результатов. Экспериментальные значения данных свойств, например, электрического сопротивления, теплопроводности, варьируются в пределах нескольких порядков величины. В настоящее время большее внимание уделяется исследованию одиночных углеродных нанотрубок или систем, содержащих нанотрубки одного типа (например, вертикально выровненные массивы углеродных нанотрубок), поскольку в этом случае появляется возможность для теоретического предсказания и практического получения структур с заданными свойствами. Современные технологии позволяют получать “чистые” УНТ, практически без примесей [1]. Будущее за технологиями, обеспечивающими контроль над составом и концентрацией примесных центров.
Одним из методов для описания ионизации атомов под действием внешних электрических полей является квазиклассический метод “мнимого времени”. Первоначально построенный для структур с квадратичным энергетическим спектром [2–4], он успешно развит для полупроводниковых узкозонных структур [5, 6] и активно применяется для современных низкоразмерных систем [7–10].
В данной работе изучается одновременное влияние постоянного и переменного квазиклассически сильных электрических полей на ионизацию примесных центров в УНТ полупроводникового типа.
ОСНОВНЫЕ УРАВНЕНИЯ
Электронная структура УНТ описывается, как правило, в рамках анализа динамики π-электронов в приближении сильной связи, учитывающем взаимодействие лишь трех соседних атомов в гексагональной структуре. В рамках данной модели закон дисперсии, описывающий свойства УНТ типа zigzag (m,0), имеет вид [11]
где γ ≈ 2.7 эВ – интеграл перескока электронов между соседними узлами кристаллической решетки, x = pxa, y = πs/m, s = 1, 2…m, $a = {{3b} \mathord{\left/ {\vphantom {{3b} {2\hbar }}} \right. \kern-0em} {2\hbar }},$ b = = 0.142 нм – расстояние между соседними атомами углерода в графене, px – квазиимпульс электрона вдоль оси УНТ. Разные знаки относятся к зоне проводимости и валентной зоне. Закон дисперсии (1) можно получить из хорошо известного энергетического спектра неограниченной графитовой плоскости (графена), накладывая периодические граничные условия, из-за которых поперечная составляющая квазиимпульса электрона принимает лишь набор дискретных значений. Продольная компонента квазиимпульса при этом остается непрерывной. Энергетический спектр электронов в нанотрубке представляет собой совокупность электронных подзон εs(k), нумеруемых угловым моментом s.Процесс перехода электрона с примесного уровня в зону проводимости представляет собой туннелирование электрона через потенциальный барьер и может носить квазиклассический характер [3]. При этом вероятность перехода (ионизации) описывается с экспоненциальной точностью в виде
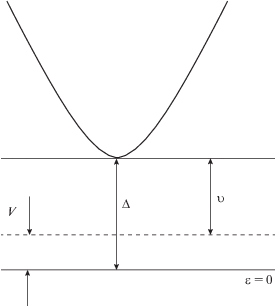
где S – классическое действие, которое набирает частица при подбарьерном движении, определяемое формулой где p(t) – импульс электрона, определяемый из классического уравнения движения, V – энергия залегания примеси. Предполагаем, что примеси находятся в УНТ на заданной глубине υ. На рис. 1. уровень энергии примеси обозначен штриховой линией. Начало отсчета энергии выбираем посередине запрещенной зоны.Электрические поля $\vec {E}$ = {E1 + E0cosωt, 0} поляризованы вдоль оси нанотрубки. Характеристики электрических полей выбираются такие, чтобы выполнялось условие применимости квазиклассического метода
Для нахождения момента начала туннелирования t0 воспользуемся условием минимума мнимой части действия
(5)
${{\left. {\frac{{\partial \operatorname{Im} (S(t))}}{{\partial t}}} \right|}_{{{{t}_{0}}}}} = 0,$что соответствует условию
Для нахождения ε(t) достаточно рассмотреть классическое уравнение движения
с начальным условием px(0) = p0x, s(0) = s0, что соответствует попаданию электрона в зону проводимости в состояние с минимальной энергией.
Подставляя решение (7) в (6), получим трансцендентное уравнение для нахождения момента начала туннелирования, корень которого чисто мнимый t0= iτ0. После перехода к безразмерным единицам получаем уравнение, которое решается численно
(8)
${{F}_{1}}{{\tilde {\tau }}_{0}} + \frac{{{{F}_{0}}}}{w}{\text{sh}}(w{{\tilde {\tau }}_{0}}) = \beta ,$Например, для УНТ типа zigzag (14, 0) для самых низших подзон (s = 5 и s = 9) мы имеем эквивалентные точки с безразмерной компонентой квазиимпульса (0, 9π/14), (π, 5π/14) и (–π, 5π/14). Отметим, что для всех подзон sin(х0) = 0, и это будет учтено в дальнейших формулах.
По формуле (3) проведен расчет классического действия, с момента времени начала туннелирования t0 до момента выхода частицы из-под барьера при t = 0. Подставляя в (3) решение (8), находим мнимую часть действия в виде интеграла
(10)
$\operatorname{Im} S = \hbar \int\limits_0^{{{{{{\tilde {\tau }}}}}_{0}}} {\left\{ {\sqrt {1 + 4{\text{ch}}\left( {{{F}_{1}}t + \frac{{{{F}_{0}}}}{w}{\text{sh}}(wt)} \right)\cos {{х}_{0}}\cos {{y}_{0}} + 4{{{\cos }}^{2}}{{y}_{0}}} + (\tilde {\upsilon } - \tilde {\Delta })} \right\}} dt,$который не выражается через элементарные функции, поэтому берется численно.
Отметим, что мнимая часть действия в (10) зависит от начальных условий, т.е. от того, в какую подзону совершается переход.
РЕЗУЛЬТАТЫ ЧИСЛЕННОГО ИССЛЕДОВАНИЯ
Выполнено численное исследование вероятности ионизации примесей в зависимости от параметров приложенных полей. На рис. 2–4 приведены характерные зависимости мнимой части действия от параметров электрических полей в безразмерных единицах для УНТ типа zigzag (13, 0) и (14, 0). С ростом частоты и амплитуды переменного и напряженности постоянного электрического поля вероятность ионизации примесей в УНТ увеличивается, что согласуется с результатами работ [7–10] и более ранних работ, посвященных узкозонным полупроводникам и сверхрешеткам [5, 6]. Увеличение числа подзон соответствует увеличению радиуса нанотрубки. Таким образом, при увеличении радиуса УНТ мнимая часть действия уменьшается, при этом вероятность ионизации возрастает. Отметим также, что при увеличении радиуса УНТ уменьшается запрещенная зона и уменьшается ширина разрешенных подзон.
Рис. 2.
Зависимость мнимой части действия S от амплитуды переменного электрического поля в безразмерных единицах при F1= 0.0002; w = 0.005; m = 13 (а), 14 (б).
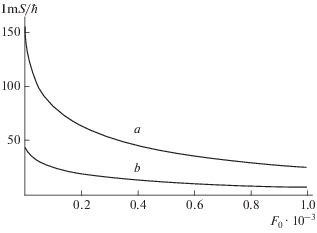
Рис. 3.
Зависимость мнимой части действия S от напряженности постоянного электрического поля в безразмерных единицах при F0= 0.0002; w = 0.005; m = 13 (а), 14 (б).
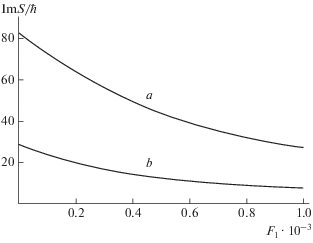
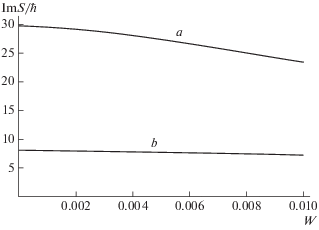
Рис. 4.
Зависимость мнимой части действия S от частоты переменного электрического поля в безразмерных единицах при F1= 0.0001; F0= 0.001; m = 13 (а), 14 (б).
Сделаем численные оценки параметров, используемых при построении графиков на рис. 2–4: значения безразмерных напряженностей F0, 1 = 10–3 соответствуют E0, 1 ≈ 105 В ⋅ см–1, а безразмерной частоте w = 0.01 соответствует ω ≈ 4 ⋅ 1013 Гц. Для УНТ типа zigzag (13, 0) для подзон s = 4 и s = 9 ширина подзоны проводимости Δe ≈ 2.0γ, Δ ≈ 1.36γ. Для УНТ типа zigzag (14, 0) для подзон s = 5 и s = = 9 ширина подзоны проводимости Δe ≈ 1.74γ, Δ ≈ ≈ 1.32γ.
При решении задачи не учитывались межзонные переходы, что соответствует выполнению условия $\hbar \omega \ll 2\Delta $ (ω $ \ll $ 1015 с–1), и тепловыми забросами электронов с примеси в подзоны – kБT $ \ll $ υ (T $ \ll $ 2 ⋅ · 103 К).
ОСНОВНЫЕ АНАЛИТИЧЕСКИЕ РЕЗУЛЬТАТЫ
Рассмотрим случай действия только постоянного электрического поля $\vec {{\rm E}}$ = {E1, 0}, ориентированного вдоль оси нанотрубки.
Для момента времени начала туннелирования ${{t}_{0}} = {{i\hbar {{{\tilde {\tau }}}_{0}}} \mathord{\left/ {\vphantom {{i\hbar {{{\tilde {\tau }}}_{0}}} \gamma }} \right. \kern-0em} \gamma }$ из (8) получен аналитический результат
По формуле (3) проведен расчет классического действия, набираемого частицей при подбарьерном движении с момента времени начала туннелирования t0 до момента выхода частицы из-под барьера при t = 0
(12)
$S = \frac{\hbar }{{{{F}_{1}}}}\left\{ {2\delta E\left( {i\frac{\beta }{2};k} \right) + i\left( {\tilde {\upsilon } - \tilde {\Delta }} \right)\beta } \right\},$Выделив мнимую часть действия [12]$,$ имеем
(13)
$\begin{gathered} \operatorname{Im} S = \frac{\hbar }{{{{F}_{1}}}}\left\{ {2\delta \left[ { - E\left( {{\text{arctg}}\left( \xi \right);1 - k} \right) + } \right.} \right. \\ \left. {\left. { + \,\,F\left( {{\text{arctg}}\left( \xi \right);1 - k} \right) + \xi \sqrt {\frac{{1 + k{{\xi }^{2}}}}{{1 + {{\xi }^{2}}}}} } \right] + \left( {\tilde {\upsilon } - \tilde {\Delta }} \right)\beta } \right\}, \\ \end{gathered} $Рассмотрим случай действия только переменного электрического поля $\vec {E}$ = {E0 cos ωt, 0}, поляризованного вдоль оси нанотрубки.
Время начала туннелирования можно получить из (8)
Аналогично предыдущему случаю воздействия на систему только постоянного электрического поля, используя формулу (3), получим выражение для действия
(15)
$\operatorname{Im} S = i\hbar \int\limits_0^{{{{{{\tilde {\tau }}}}}_{0}}} {\sqrt {1 + 4\cos {{x}_{0}}\cos {{y}_{0}}{\text{ch}}\left( {\frac{{{{F}_{0}}}}{w}{\text{sh}}(wt)} \right) + 4{{{\cos }}^{2}}{{y}_{0}}} dt + (\tilde {\nu } - \tilde {\Delta }){{{\tilde {\tau }}}_{0}}} .$Интеграл в (15) не выражается в элементарных функциях, поэтому для получения аналитического результата рассмотрим несколько частных случаев.
В случае ${{{{F}_{0}}} \mathord{\left/ {\vphantom {{{{F}_{0}}} w}} \right. \kern-0em} w} \ll 1,$ ограничившись первым членом разложения гиперболического косинуса в ряд Тейлора, после преобразования и выделения мнимой части действия, имеем
(16)
$\begin{gathered} \operatorname{Im} S = \frac{\hbar }{w}\left\{ {\delta \left[ { - E({\text{arctg}}(\xi ),1 - k{\kern 1pt} ') + } \right.} \right. \\ + \,\,\left. {F({\text{arctg}}(\xi ),1 - k{\kern 1pt} ') + \xi \sqrt {\frac{{1 + k{\kern 1pt} '{{\xi }^{2}}}}{{1 + {{\xi }^{2}}}}} } \right] + \\ \left. { + \,\,(\tilde {\nu } - \tilde {\Delta }){\text{arsh}}\left( {\frac{{w\beta }}{{{{F}_{0}}}}} \right)} \right\}, \\ \end{gathered} $В противоположном предельном случае F0/w $ \gg $ 1 после преобразования получаем выражение для мнимой части действия
(17)
$\begin{gathered} \operatorname{Im} S = \frac{\hbar }{w}{\text{arsh}}\left( {\frac{{w\beta }}{{{{F}_{0}}}}} \right)\left\{ {\frac{{2\delta }}{\beta }\left[ { - E({\text{arctg}}(\xi {\kern 1pt} '),1 - k)} \right. + } \right. \\ \left. {\left. { + \,\,F({\text{arctg}}(\xi {\kern 1pt} '),1 - k) + \xi {\kern 1pt} '\sqrt {\frac{{1 + k{{\xi }^{{'2}}}}}{{1 + {{\xi }^{{'2}}}}}} } \right] + (\tilde {\nu } - \tilde {\Delta })} \right\}, \\ \end{gathered} $В случае, когда в дополнение к условию F0/w $ \gg $ 1 еще и ${\beta \mathord{\left/ {\vphantom {\beta 2}} \right. \kern-0em} 2} \ll 1,$ выражение для мнимой части действия значительно упрощается
(18)
$\begin{gathered} \operatorname{Im} S = \frac{\hbar }{w}{\text{arsh}}\left( {\frac{{w\beta }}{{{{F}_{0}}}}} \right) \times \\ \times \,\left\{ {\delta \int\limits_0^1 {\sqrt {1 + k{\kern 1pt} ''{{\beta }^{2}}{{z}^{2}}} dz} + (\tilde {\nu } - \tilde {\Delta })} \right\}, \\ \end{gathered} $(19)
$\begin{gathered} \operatorname{Im} S = \frac{{\hbar \beta }}{{{{F}_{0}}}} \times \\ \times \,\,\left\{ {\frac{\delta }{2}(\sqrt {1 + k{\kern 1pt} ''{{\beta }^{2}}} + \frac{{{\text{arsh}}(\sqrt {k{\kern 1pt} ''{{\beta }^{2}}} )}}{{\sqrt {k{\kern 1pt} ''{{\beta }^{2}}} }}) + (\tilde {\nu } - \tilde {\Delta })} \right\}. \\ \end{gathered} $Как видно из (19), в данном предельном случае пропадает зависимость мнимой части действия, а, следовательно, и вероятности ионизации примесей от частоты переменного электрического поля.
ЗАКЛЮЧЕНИЕ
Получено выражение для нахождения вероятности ионизации примесей статическими и переменными электрическими полями в квазиклассическом приближении в однослойных УНТ полупроводникового типа. Электрические поля поляризованы вдоль оси УНТ. В результате численного исследования показано, что при увеличении таких параметров как: частота, амплитуда переменного и напряженность постоянного электрического поля, возрастает вероятность ионизации примесей в УНТ. С увеличением радиуса УНТ при одинаковой глубине залегания примесных центров и параметров приложенных полей вероятность ионизации примесей возрастает. Получено аналитическое выражение для вероятности ионизации примесей в УНТ, находящихся в постоянном электрическом поле. В случае воздействия переменного электрического поля получены аналитические выражения для вероятности ионизации примесей в предельных случаях. Проведено сравнение ионизации примесей в УНТ с щелевыми модификациями графена и полупроводниковыми структурами.
Список литературы
Zhukova E.A., Urvanov S.A., Karaeva A.R. et al. // Mater. Today. Proc. 2018. V. 5. No. 12. Art. No. 25948.
Попов В.С., Кузнецов В.П., Переломов А.М. // ЖЭТФ. 1967. № 53. С. 331; Popov V.S., Kuznetsov V.P., Perelomov A.M. // J. Exp. Theor. Phys. 1968. V. 26. P. 222.
Базь А.И., Зельдович Я.Б., Переломов А.М. Рассеяние, реакции и распады в нерелятивистской квантовой механике. М.: Наука, 1989.
Попов В.С., Карнаков Б.М., Мур В.Д. // ЖЭТФ. 1998. № 113. V. 5. С. 1579; Popov V.S., Karnakov B.M., Mur V.D. // J. Exp. Theor. Phys. 1998. V. 86. No. 5. P. 860.
Крючков С.В., Сыродоев Г.А. // Изв. вузов СССР. Радиофиз. 1990. № 6. С. 762.
Крючков С.В., Сыродоев Г.А. // ФТП. 1988. Т. 22. № 9. С. 1695.
Глазов С.Ю., Бадикова П.В. // Журн. нано-электрон. физ. 2018. № 2. Т. 10. С. 02020.
Бадикова П.В., Глазов С.Ю. // Изв. РАН. Сер. физ. 2018. Т. 82. № 11. С. 1536; Badikova P.V., Glazov S.Yu. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. No. 11. P. 1399.
Бадикова П.В., Глазов С.Ю., Сыродоев Г.А. // ФТП. 2019. Т. 53. № 7. С. 927; Badikova P.V., Glazov S.Yu., Syrodoev G.A. // Semicond. 2019. V. 53. No. 7. P. 911.
Бадикова П.В., Глазов С.Ю., Сыродоев Г.А. // Изв. РАН. Сер. физ. 2020. Т. 84. № 1. С. 38; Badikova P.V., Glazov S.Yu., Syrodoev G.A. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 1. P. 30.
Максименко С.А., Слепян Г.Я. // Радиотехн. и электроника. 2002. Т. 47. № 3. С. 261; Maksimenko S.A., Slepyan G.Ya. // J. Commun. Technol. Electron. 2002. V. 47. No. 3. P. 235.
Абрамовиц М., Стиган И. Справочник по специальным функциям. Москва: Наука, 1979.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая