Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 42-46
О возможности генерации встречных ортогонально-поляризованных мод в кристалле с регулярной доменной структурой с учетом дифракции и формирования квантовых фантомных изображений
А. В. Белинский 1, Р. Сингх 1, *
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”, Физический факультет
Москва, Россия
* E-mail: ranjit.singh@mail.ru
Поступила в редакцию 24.08.2021
После доработки 06.09.2021
Принята к публикации 22.09.2021
- EDN: JTTPCE
- DOI: 10.31857/S0367676522010045
Аннотация
Рассмотрена реализация вырожденного параметрического процесса, когда 2 ортогонально-поляризованные встречные моды рождаются и распространяются в кристаллe с регулярной доменной структурой. Предложена схема формирования квантовых фантомных изображений. Установлено, что дифракция пучков практически не влияет на корреляционные коэффициенты 2-го порядка, что обуславливает хорошие перспективы получения фантомных изображений высокого качества, поскольку именно дифракция, как правило, наиболее губительно действует на их пространственное разрешение.
ВВЕДЕНИЕ
Генерация встречных ортогонально-поляризованных мод традиционно рассматривается в изотропных кубически нелинейных средах [1]. Встречные моды удобно использовать для формирования квантовых фантомных изображений [2]. Отметим, что в квадратичных монодоменных кристаллах рождение и генерация встречных мод отсутствует в связи с отсутствием фазового синхронизма между взаимодействующими пучками. В то же время, ранее теоретически и экспериментально рассматривалось встречное взаимодействие в кристаллах с регулярной доменной структурой (РДС-кристаллах), когда все взаимодействующие моды имели одинаковую поляризацию в том числе спонтанное параметрическое рассеяние [3, 4]. Недавние работы [5–8] теоретически и экспериментально рассматривали рождение встречных поляризованных мод с учетом только спонтанного параметрического процесса и минуя квантовые корреляции и поляризационные характеристики мод. Также отметим работы [9–13], посвященные теме абсолютного измерения яркости терагерцовых волн, где рассмотрены процессы спонтанного параметрического процесса с генерацией не только попутных, но и встречных терагерцовых волн в РДС-кристаллах.
Данная работа посвящена возможности рождения и реализации двух нелинейных процессов (спонтанный параметрический процесс, суммарная генерация частот) и изучению квантовых статистических характеристик ортогонально-поляризованных встречных мод, что позволяет их легко разделить в экспериментальных схемах. Для реализации таких процессов можно использовать метаматериалы, например, регулярные доменные структуры (РДС), чтобы компенсировать фазовый набег за счет обратной решетки волнового вектора или чередования значения восприимчивости ${{\chi }^{{\left( 2 \right)}}}$ с периодом домена $\Lambda $ (см. рис. 1).
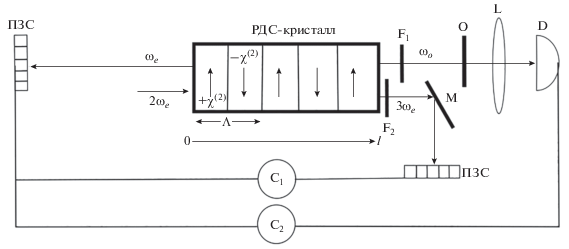
Рис. 1.
Схема рождения встречных ортогонально поляризационных мод внутри РДС-кристалла и формирования фантомного изображения объекта $O$ на матрице детекторов ПЗС. Моды имеют вырожденные частоты с поляризациями $o$ (обыкновенная) и $e$ (необыкновенная). Накачка на частоте $2{{\omega }_{e}}$ в расчетах предполагается неистощимой, а остальные моды находятся в начальном вакуумном состоянии. Для разделения частот используются фильтры ${{{\text{F}}}_{{\text{1}}}}$ и ${{{\text{F}}}_{2}}.$ Одна из встречных мод – сигнальная на частоте ${{\omega }_{o}}$ – облучает прозрачный объект, затем объектив ${\text{L}}$ собирает пучки, и они регистрируются на интегральном детекторе ${\text{D}}.$ Холостая мода на частоте ${{\omega }_{e}}$ и мода на частоте $3{{\omega }_{e}},$ используются для восстановления изображения объекта с пространственной регистрацией фотонов на матрице детекторов (ПЗС). ${\text{M}}$ – зеркало, которое отражает моду на частоте $3{{\omega }_{e}}.$ Моды на частотах $\left( {{{\omega }_{e}},{{\omega }_{o}}} \right)$ и $\left( {{{\omega }_{e}},3{{\omega }_{e}}} \right)$ попарно коррелированы. Корреляторы ${{{\text{C}}}_{{1,2}}}$ фиксируют одновременную регистрацию фотонов.
ПРОЦЕССЫ В РДС-КРИСТАЛЛЕ
Пусть четыре стационарные, плоские, монохроматические моды, характеризуемые операторами уничтожения фотона ${{\hat {A}}_{{1e}}},$ ${{\hat {A}}_{{1o}}},$ ${{\hat {A}}_{{2e}}}$ и ${{\hat {A}}_{{3e}}}$ коллинеарно распространяются внутри РДС-кристалла с квадратичной нелинейностью. Нелинейные оптические процессы, которые описывают эффективное взаимодействие и распространение четырех мод внутри РДС-кристалла имеют вид:
(1)
$2{{\omega }_{e}} = {{\omega }_{o}} + {{\omega }_{e}},\,\,\,\,\delta {{k}_{1}} = {{k}_{{2e}}} + {{k}_{{1e}}} - {{k}_{{1o}}} + {{m}_{1}}{{G}_{1}},$(2)
${{\omega }_{e}} + 2{{\omega }_{e}} = 3{{\omega }_{e}},\,\,\,\,\delta {{k}_{2}} = {{k}_{{3e}}} - {{k}_{{2e}}} + {{k}_{{1e}}} + {{m}_{2}}{{G}_{2}},$ПОВОРОТ ДОМЕНА И КОМПОНЕНТЫ ТЕНЗОРОВ ${{\chi }^{{(1)}}}$ И ${{\chi }^{{(2)}}}$
Рассматрим РДС-кристалл на основе ${\text{LiNb}}{{{\text{O}}}_{{\text{3}}}}.$ Определим знаки перед компонентами тензора второго (линейная восприимчивость ${{\chi }^{{(1)}}}$) и третьего (нелинейная восприимчивость ${{\chi }^{{(2)}}}$) рангов. Отметим, что, тензор третьего ранга $\chi _{{m,n,p}}^{{(2)}}$ симметричен относительно перестановки двух последних индексов, то есть, $\chi _{{m,n,p}}^{{(2)}} = \chi _{{m,p,n}}^{{(2)}}$ и обладает симметрией класса ${{C}_{{3{{\nu }}}}}$ [14]. Известно, что данный кристалл имеет только три независимых ненулевых компонента $\chi _{{z,z,z}}^{{\left( 2 \right)}}\left( { = {{d}_{{33}}}} \right),$ $\chi _{{y,y,y}}^{{\left( 2 \right)}}\left( { = {\kern 1pt} {{d}_{{22}}}} \right)$ = = $ - \chi _{{x,y,x}}^{{\left( 2 \right)}}\, = - \chi _{{y,x,x}}^{{\left( 2 \right)}}$ и $\chi _{{x,x,z}}^{{\left( 2 \right)}}\left( { = {{d}_{{15}}}} \right)$ = $\chi _{{y,y,z}}^{{(2)}}$ = $\chi _{{z,x,x}}^{{\left( 2 \right)}}\, = \chi _{{z,y,y}}^{{\left( 2 \right)}}.$
Для определения знака перед компонентами связи необходимо применить матрицу вращения $R$ на ${{\chi }^{{\left( 2 \right)}}}$ [14]. Поворот домена кристалла вокруг оси $x$ на угол $\alpha $ и знак минус перед ${{\chi }^{{\left( 2 \right)}}}$ задается следующим уравнением [14]
(3)
$\tilde {\chi }_{{j,k,l}}^{{(2)}}(\alpha ) = \sum\limits_{m,n,p = 1}^3 {R_{{j,m}}^{x}} (\alpha )R_{{k,n}}^{x}(\alpha )R_{{l,p}}^{x}(\alpha )\chi _{{m,n,p}}^{{(2)}},$(4)
$\tilde {\chi }_{{j,k}}^{{(1)}}(\alpha ) = \sum\limits_{l,m = 1}^3 {R_{{j,l}}^{x}} (\alpha )R_{{k,m}}^{x}(\alpha )\chi _{{l,m}}^{{(1)}}.$Отметим, что поворот домена против часовой стрелки на угол $\alpha = \pi $ вокруг оси $x$ не меняет знаки главных компонентов тензора $\tilde {\chi }_{{j,j}}^{{(1)}} = \chi _{{j,j}}^{{(1)}}.$ Тензор ${{\chi }^{{(1)}}}$ является симметричным, поэтому ее недиагональные компоненты после поворота можно привести к диагональному виду, т.е., недиагональные элементы можно свести к нулю [14]. В результате поворота компоненты тензора ${{\chi }^{{(2)}}}$ и значения нелинейных эффективных коэффициентов меняют знак с положительного на отрицательный.
СИСТЕМА ОПЕРАТОРНЫХ УРАВНЕНИЙ
Система операторных уравнений, которая описывает рассматриваемые нелинейные процессы (1), (2) имеет вид
(5)
$\begin{gathered} \frac{\partial }{{\partial z}}{{{\hat {A}}}_{{1o}}}(x,y,z) + i\frac{1}{{2k_{{1o}}^{{(z)}}}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right){{{\hat {A}}}_{{1o}}}(x,y,z) = \\ = - i\hat {A}_{{1e}}^{\dag }(x,y,z), \\ \end{gathered} $(6)
$\begin{gathered} \frac{\partial }{{\partial z}}\hat {A}_{{1e}}^{\dag }(x,y,z) + i\frac{1}{{2k_{{1o}}^{{(z)}}}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)\hat {A}_{{1e}}^{\dag }(x,y,z) = \\ = - i{{{\hat {A}}}_{{1o}}}(x,y,z) - i\hat {A}_{{3e}}^{\dag }(x,y,z), \\ \end{gathered} $(7)
$\begin{gathered} \frac{\partial }{{\partial z}}\hat {A}_{{3e}}^{\dag }(x,y,z) - i\frac{1}{{2k_{{3e}}^{{(z)}}}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right)\hat {A}_{{3e}}^{\dag }(x,y,z) = \\ = i\hat {A}_{{1e}}^{\dag }(x,y,z). \\ \end{gathered} $(8)
${{\hat {A}}_{{jp}}}\left( {\vec {r},\ell } \right) = \int\limits_{ - \infty }^\infty {{{{\hat {a}}}_{{jp}}}\left( {\vec {\varkappa },\ell } \right){{e}^{{i\vec {r} \cdot \vec {\varkappa }}}}{{d}^{2}}\vec {\varkappa }} ,$(9)
$\hat {A}_{{jp}}^{\dag }\left( {\vec {r},\ell } \right) = \int\limits_{ - \infty }^\infty {\hat {a}_{{jp}}^{\dag }\left( {\vec {\varkappa },\ell } \right){{e}^{{ - i\vec {r} \cdot \vec {\varkappa }}}}{{d}^{2}}\vec {\varkappa }} ,$Корректность решения линейной системы операторных уравнений (5)–(7) и расчетов проверялась выполнением коммутационных соотношений. Конкретный вид решения опущен в связи с громоздкостью.
КВАНТОВЫЕ СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛЯРИЗАЦИИ МОД
Для изучения квантовых статистических характеристик [15, 16] среднего числа фотонов, коэффициентов корреляций 2-го порядка и степени поляризации между ортогонально-поляризованными модами на частотах ${{\omega }_{o}}$ и ${{\omega }_{e}}$ вычислены следующие величины.
Среднее число фотонов
(10)
$\begin{gathered} {{N}_{{1o,3e}}}(\vec {\varkappa },\ell ) = \left\langle {\hat {a}_{{1o,3e}}^{\dag }(\vec {\varkappa },\ell ){{{\hat {a}}}_{{1o,3e}}}(\vec {\varkappa },\ell )} \right\rangle , \\ {{N}_{{1e}}}(\vec {\varkappa },0) = \left\langle {\hat {a}_{{1e}}^{\dag }(\vec {\varkappa },0){{{\hat {a}}}_{{1e}}}(\vec {\varkappa },0)} \right\rangle . \\ \end{gathered} $Коэффициенты корреляции фотонов между модами
(11)
$g_{{1o,1e}}^{{(2)}}(\vec {\varkappa },\ell ) = \frac{{\left\langle {{{{\hat {N}}}_{{1o}}}(\vec {\varkappa },\ell ){{{\hat {N}}}_{{1e}}}(\vec {\varkappa },0)} \right\rangle }}{{{{N}_{{1o}}}(\vec {\varkappa },\ell ){{N}_{{1e}}}(\vec {\varkappa },0)}},$(12)
$g_{{1o,3e}}^{{(2)}}(\vec {\varkappa },\ell ) = \frac{{\left\langle {{{{\hat {N}}}_{{1o}}}(\vec {\varkappa },\ell ){{{\hat {N}}}_{{3e}}}(\vec {\varkappa },\ell )} \right\rangle }}{{{{N}_{{1o}}}(\vec {\varkappa },\ell ){{N}_{{3e}}}(\vec {\varkappa },\ell )}},$(13)
$g_{{1e,3e}}^{{(2)}}(\vec {\varkappa },\ell ) = \frac{{\left\langle {{{{\hat {N}}}_{{1e}}}(\vec {\varkappa },0){{{\hat {N}}}_{{3e}}}(\vec {\varkappa },\ell )} \right\rangle }}{{{{N}_{{1e}}}(\vec {\varkappa },0){{N}_{{3e}}}(\vec {\varkappa },\ell )}}.$Степень поляризации взаимодействующих ортогональных мод
(14)
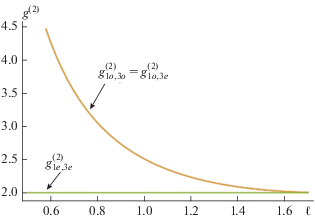
$DoP(\vec {\varkappa },\ell ) = \frac{{\sqrt {\left\langle {\hat {S}_{1}^{2}(\vec {\varkappa },\ell ) + \hat {S}_{2}^{2}(\vec {\varkappa },\ell ) + \hat {S}_{3}^{2}(\vec {\varkappa },\ell )} \right\rangle } }}{{\left\langle {{{{\hat {S}}}_{0}}(\vec {\varkappa },\ell )\left( {{{{\hat {S}}}_{0}}(\vec {\varkappa },\ell ) + 2} \right)} \right\rangle }},$Усреднение фотонов, коэффициентов корреляций и степени поляризации (8)–(11) произведены в случае, когда мода накачки не истощалась, а остальные моды находились в вакуумном состоянии (см. рис. 2 и 3). Значения коэффициентов корреляций и степени поляризации вычислялись, когда мода на частоте ${{\omega }_{e}}$ находилась в начальной точке кристалла 0, а моды на частотах ${{\omega }_{o}}$ и $3{{\omega }_{e}}$- в конечной точке $\ell .$ Рисунок 2 показывает, что имеется высокая корреляции между модами $\left( {{{\omega }_{o}},{{\omega }_{e}}} \right),$ $\left( {{{\omega }_{o}},3{{\omega }_{e}}} \right)$ и $\left( {{{\omega }_{e}},3{{\omega }_{e}}} \right).$ С возрастанием длины РДС-кристалла значение коэффициентов корреляций стремится к 2.
ЗАКЛЮЧЕНИЕ
Впервые рассмотрена возможность реализации вырожденного параметрического процесса, когда две ортогонально-поляризованные встречные моды рождаются и распространяются внутри РДС-кристалла. Найдены длины волны, периоды решеток и порядки квазисинхронизма в случае LiNbO3, когда оба нелинейных процесса (1), (2) одновременно могут эффективно реализовываться.
Установлено, что среднее число фотонов (10), корреляционные коэффициенты второго порядка (11)–(13) слабо зависят от дифракции внутри РДС-кристалла. Это дает хорошие шансы получать фантомные изображения высокого качества, потому что дифракция, как правило, наиболее губительно действует на пространственное разрешение [17]. Опущены кривые корреляций и степень поляризации при разных значениях поперечной части волнового числа, так как поведение кривых почти не меняется, что и подтверждает независимость взаимодействующих пучков от условий фазового синхронизма.
На рис. 2 приведены значения коэффициентов корреляции 2-го порядка. При ${{g}^{{\left( 2 \right)}}} > 1$ преобладают фотоны парные, коррелированные в двух модах. Кривые корреляций показывают, что встречные ортогонально-поляризованные моды могут стать хорошими кандидатами для формирования квантовых фантомных изображений аналогично, как в случае встречного четырехфотонного cмешения в формировании фантомных изображений с помощью кубической нелинейной среды [2].
Отмечено, что дифракция внутри РДС-кристалла слабо влияет на эффективность нелинейных процессов по сравнению с попутным взаимодействием.
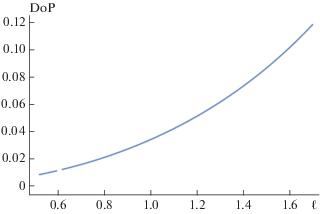
Показано, что степень поляризации не равна нулю (см. рис. 3). Это связано с тем, что фотон моды на частоте ${{\omega }_{e}}$ участвует в процессе (3).
Отметим, что волноводы, интегральные схемы на основе квадратичной нелинейности (РДС-кристалл на базе ${\text{LiNb}}{{{\text{O}}}_{3}}$ [8]) могут стать хорошим кандидатом для задач эндоскопии, так как встречные ортогонально-поляризованные коррелированные моды также могут содержать поляризационные характеристики изучаемого объекта при формировании фантомных изображений. Встречные моды в рассматриваемом РДС-кристалле слабо зависят от дифракции, что важно для формирования квантовых фантомных изображений высокого качества.
Исследование выполнено при поддержке Российского научного фонда (проект № 21-12-00155).
Список литературы
Yariv A., Pepper D. // Opt. Lett. 1977. V. 1. No. 1. P. 16.
Белинский А.В., Сингх Р. // ЖЭТФ. 2021. Т. 159. № 2. С. 258.
Волков В.В., Чиркин А.С. // Квант. электрон. 1999. Т. 26. № 1. С. 82.
Волоховский В.В., Чиркин А.С. // Квант. электрон. 2001. Т. 31. № 5. С. 437.
Luo K., Ansari V., Massaro M. et al. // Opt. Expr. 2020. V. 28. P. 3215.
Mutter P., Zukauskas A., Viotti A. et al. // EPJ Web Conf. 2020. V. 243. Art. No. 18003.
Booth M.C., Atature M., Guiseppe G.Di. et al. // Proc. 15th Ann. Meeting. IEEE Lasers Electro-Opt. Soc. V. 1. (Glasgow, 2002). P. 83
Duan J., Zhang J., Zhu Y. et al. // J. Opt. Soc. Amer. B. 2020. V. 37. No. 7. P. 2139.
Kornienko V.V., Kitaeva G.K., Sedlmeir F. et al. // APL Photon. 2018. V. 3. No. 5. Art. No. 051704.
Kitaeva G.K., Yakunin P.V., Kornienko V.V., Penin A.N. // Appl. Phys. B. 2014. V. 116. No. 4. P. 929.
Kuznetsov K.A., Kovalev S.P., Kitaeva G.K. et al. // Appl. Phys. B. 2010. V. 101. No. 4. P. 811.
Китаева Г.Х., Пенин А.Н., Тучак А.Н. и др. // Письма в ЖЭТФ. 2010. Т. 92. № 5. С. 327.
Kitaeva G.K., Kovalev S.P., Penin A.N. et al. // J. Infrared Millimeter Terahertz Waves. 2011. V. 32. No. 10. P. 1144.10.1007/s10762-011-9780-y
Най Д. Физические свойства кристаллов. М.: ИЛ, 1960.
Чиркин А.С. // Опт. и спектроск. 2015. Т. 119. № 3. С. 397.
Белинский А.В., Сингх Р. // Изв. РАН. Сер. физ. 2021. Т. 85. № 1. С. 45; Belinsky A.V., Singh R. // Bull. Russ. Acad. Sci. Phys. 2021. V. 85. No. 1. P. 39.
Белинский А.В. // Вестн. Моск. ун-та. Сер. физ. и астрон. 2018. № 5. С. 3.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая