1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 1, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 63-67

Трехмерные импульсы Матьё и Бесселя в массиве примесных углеродных нанотрубок

М. Б. Белоненко 1, *, Н. Н. Конобеева 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Волгоградский государственный университет”
Волгоград, Россия

* E-mail: mbelonenko@yandex.ru

Поступила в редакцию 24.08.2021
После доработки 06.09.2021
Принята к публикации 22.09.2021

Полный текст (PDF)

Аннотация

Исследовано распространение трехмерных импульсов с поперечным сечением Матьё и Бесселя в массиве полупроводниковых углеродных нанотрубок с примесями. На основании уравнений Максвелла получено эффективное уравнение на векторный потенциал электромагнитного поля. Проанализирована зависимость формы импульса от параметров примеси и функций Матьё и Бесселя.

ВВЕДЕНИЕ

Как хорошо известно, существуют локализованные решения волнового уравнения, которые в идеальном случае не испытывают дифракционных или дисперсионных эффектов во время их распространения [1–3]. Такие волны сохраняют свой профиль поперечной интенсивности при распространении в свободном пространстве. Отметим, что в цилиндрической системе координат решения волнового уравнения для бездифракционного пучка задаются с помощью функций Бесселя, а в эллиптической системе координат – функциями Матьё [4, 5] Такие локализованные импульсы представляют большой интерес для беспроводной и оптической связи, медицинской визуализации, лазерной хирургии, нелинейной оптики и др.

В оптике бездифракционное распространение пучков может быть получено в удобных средах [6], таких как волноводные или нелинейные материалы. Привлекательной с этой точки зрения средой являются углеродные нанотрубки (УНТ), обладающие целым рядом уникальных свойств с большим практическим потенциалом [7]. Было проведено много исследований, касающихся эволюции пучков разного профиля в среде с УНТ [8‒12]. Все они продемонстрировали стабилизирующее воздействие среды с нанотрубками на распространяющиеся в ней импульсы. Прим этом вне рассмотрения остался вопрос влияния примесей в УНТ, которые могут оказать существенное воздействие на эволюцию импульсов. В данной работе мы будем исследовать электромагнитные волны с поперечным сечением Бесселя и Матьё.

ПОСТАНОВКА ЗАДАЧИ

Исследуем особенности эволюции трехмерных предельно коротких электромагнитных импульсов (ПКИ) в массиве зигзагообразных углеродных нанотрубок. Будем считать, что по объему массива нанотрубок равномерно распределена примесь, которая для определенности имеет четыре уровня.

Учтем, что волновой вектор перпендикулярен оси нанотрубок (ось Oy), а вектор его электрического поля направлен вдоль оси трубок Oz.

Вектор потенциал имеет вид: $\vec {A}$ = (0, 0, A(x, y, z)) плотность электрического тока $\vec {j} = \left( {0,0,j\left( {x,y,z} \right)} \right).$

Для компоненты электрического поля, направленной вдоль оси УНТ (с учетом: $\vec {E} = - {{c}^{{ - 1}}}{{\partial{ \vec {A}}} \mathord{\left/ {\vphantom {{\partial{ \vec {A}}} {\partial t}}} \right. \kern-0em} {\partial t}},$ запишем трехмерное волновое уравнение в цилиндрической системе координата для импульсов Бесселя (1a) и в параболической системе координат для импульсов Матьё (1б):

(1a)
$\frac{\varepsilon }{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{t}^{2}}}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial{ \vec {A}}}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{\varphi }^{2}}}} + 4\pi j\left( {\vec {A}} \right),$
(1б)
$\begin{gathered} \frac{\varepsilon }{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{t}^{2}}}} = \frac{1}{{{{\sigma }^{2}} + {{\tau }^{2}}}}\left( {\frac{1}{\sigma }\frac{\partial }{{\partial \sigma }}\left( {\sigma \frac{{\partial{ \vec {A}}}}{{\partial \sigma }}} \right) + \frac{1}{\tau }\frac{\partial }{{\partial \tau }}\left( {\tau \frac{{\partial{ \vec {A}}}}{{\partial \tau }}} \right)} \right) + \\ + \,\,\frac{1}{{{{\sigma }^{2}}{{\tau }^{2}}}}\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{\varphi }^{2}}}} + 4\pi j\left( {\vec {A}} \right), \\ \end{gathered} $
где ε – диэлектрическая проницаемость среды, c – скорость света, (r, z, φ) – координаты в цилиндрической системе координат, (σ, τ, φ) – координаты в параболической системе координат.

Запишем стандартное выражение для плотности тока [13]:

(2)
$j = 2e\sum\limits_{s = 1}^m {\int\limits_{ZB} {{{\nu }_{s}}\left( p \right)f\left( {p,s} \right)dp} } ,$
где e – заряд электрона, p – компонента квазиимпульса электрона проводимости вдоль оси нанотрубки, ${{\nu }_{s}}\left( p \right) = {{\partial {{\varepsilon }_{{imp}}}\left( p \right)} \mathord{\left/ {\vphantom {{\partial {{\varepsilon }_{{imp}}}\left( p \right)} {\partial p}}} \right. \kern-0em} {\partial p}}$ – скорость электронов, $f\left( {p,s} \right)$ – функция распределения Ферми, ${{\varepsilon }_{{imp}}}\left( p \right)$ – закон дисперсии с учетом примесей [14]:

(3)
$\begin{gathered} {{\varepsilon }_{{imp}}}\left( {p,s} \right) = 0.5\left( {R + Q + } \right. \\ \left. { + \,\,\sqrt {{{{\left( {R - Q} \right)}}^{2}} - 4\left( {2D \cdot \Delta \left( {p,s} \right) - \Delta {{{\left( {p,s} \right)}}^{2}} - {{D}^{2}}} \right)} } \right) \\ \end{gathered} $

R, Q – параметры, описывающие переходы электрона между примесными уровнями и подрешетками нанотрубок, D – параметр, описывающий переходы между двумя подрешетками УНТ, $\Delta \left( {p,s} \right)$ – закон дисперсии для электронов углеродных нанотрубок без учета примеси [15, 16].

В работе [13] показано, что накопление заряда, возникающее из-за неоднородности поля вдоль оси, не оказывает существенного влияния на распространение поля предельно короткого импульса. Поэтому производной по углу в данном приближении можно пренебречь. В этом случае получаем эффективное уравнение на векторный потенциал для импульса Бесселя (4a) и Матьё (4б):

(4a)
$\begin{gathered} \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial A}}{{\partial r}}} \right) + \frac{{{{\partial }^{2}}A}}{{\partial {{z}^{2}}}} - \frac{\varepsilon }{{{{c}^{2}}}}\frac{{{{\partial }^{2}}A}}{{\partial {{t}^{2}}}} + \\ + \,\,\sum\limits_{k = 1}^\infty {\frac{{4e{{n}_{0}}{{f}_{k}}}}{c}{\text{sin}}\left( {\frac{{kaeA}}{c}} \right)} = 0, \\ \end{gathered} $
(4б)
$\begin{gathered} \frac{1}{{{{\sigma }^{2}} + {{\tau }^{2}}}}\left( {\frac{1}{\sigma }\frac{\partial }{{\partial \sigma }}\left( {\sigma \frac{{\partial A}}{{\partial \sigma }}} \right) + \frac{1}{\tau }\frac{\partial }{{\partial \tau }}\left( {\tau \frac{{\partial A}}{{\partial \tau }}} \right)} \right) - \frac{\varepsilon }{{{{c}^{2}}}}\frac{{{{\partial }^{2}}A}}{{\partial {{t}^{2}}}} + \\ + \,\,\sum\limits_{k = 1}^\infty {\frac{{4e{{n}_{0}}{{f}_{k}}}}{c}{\text{sin}}\left( {\frac{{kaeA}}{c}} \right)} = 0, \\ \end{gathered} $

n0 – концентрация электронов,

(5)
${{f}_{k}} = \sum\limits_s {{{a}_{{sk}}}} \int\limits_{BZ} {dp{\text{cos}}\left( {pk} \right)} \frac{{{\text{exp}}\left( { - {{{{\varepsilon }_{{imp}}}\left( {p,s} \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{imp}}}\left( {p,s} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right)}}{{{\text{exp}}\left( { - {{{{\varepsilon }_{{imp}}}\left( {p,s} \right)} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{imp}}}\left( {p,s} \right)} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}} \right) + 1}},$

kB – постоянная Больцмана, T – температура, ask – коэффициенты в разложении закона дисперсии электронов (3) в ряд Фурье:

(6)
${{\varepsilon }_{{imp}}}\left( {p,s} \right) = \frac{1}{{2\pi }}\sum\limits_{s = 1}^m {\sum\limits_{k = 1}^\infty {{{a}_{{sk}}}{\text{cos}}\left( {pk} \right)} } ,$
(7)
${{a}_{{sk}}} = \int\limits_{BZ} {dp{\text{cos}}\left( {pk} \right){{\varepsilon }_{{imp}}}\left( {p,s} \right)} .$

Интегрирование ведется по первой зоне Бриллюэна. Отметим, что сумме по k мы учитываем первые 10 слагаемых ввиду убывания коэффициентов fk [17].

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Проведено численное моделирование уравнений (4a) и (4б). Начальные условия для импульса выбирались следующим образом:

(8a)
$\begin{gathered} A\left( {r,z,0} \right) = {{A}_{0}}{\text{exp}}\left( { - \frac{{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}}}{{\gamma _{z}^{2}}}} \right){\text{exp}}\left( { - \frac{r}{\gamma }} \right), \\ \frac{{dA\left( {r,z,0} \right)}}{{dt}} = \frac{{2{{A}_{0}}\upsilon \left( {z - {{z}_{0}}} \right)}}{{\gamma _{z}^{2}}}{{J}_{0}}\left( {\frac{r}{{{{\gamma }_{r}}}}} \right) \times \\ \times \,\,{\text{exp}}\left( { - \frac{{{{{\left( {z - {{z}_{0}}} \right)}}^{2}}}}{{\gamma _{z}^{2}}}} \right){\text{exp}}\left( { - \frac{r}{\gamma }} \right), \\ \end{gathered} $
(8б)
$\begin{gathered} A\left( {\sigma ,\tau ,0} \right) = {{A}_{0}}{\text{c}}{{{\text{e}}}_{0}}\left( {1,q} \right){\text{Jce}}\left( {\frac{\tau }{{{{\gamma }_{{{\tau }}}}}}} \right) \times \\ \times \,\,{\text{exp}}\left( { - \frac{{{{{\left( {\sigma - {{\sigma }_{0}}} \right)}}^{2}}}}{{\gamma _{{{\sigma }}}^{2}}}} \right){\text{exp}}\left( { - \frac{\tau }{\gamma }} \right), \\ \frac{{dA\left( {\sigma ,\tau ,0} \right)}}{{dt}} = \frac{{2{{A}_{0}}\upsilon \left( {\sigma - {{\sigma }_{0}}} \right){\text{с}}{{{\text{e}}}_{0}}\left( {1,q} \right)}}{{\gamma _{{{\sigma }}}^{2}}} \times \\ \times \,\,{\text{Jce}}\left( {\frac{\tau }{{{{\gamma }_{{{\tau }}}}}}} \right){\text{exp}}\left( { - \frac{{{{{\left( {\sigma - {{\sigma }_{0}}} \right)}}^{2}}}}{{\gamma _{{{\sigma }}}^{2}}}} \right){\text{exp}}\left( { - \frac{\tau }{\gamma }} \right), \\ \end{gathered} $
где A0 – амплитуда электромагнитного импульса на входе в среду с УНТ, $\upsilon $ – скорость импульса при входе в среду, ${{\gamma }_{i}}$ – ширина импульса вдоль направления $i = \left( {r,z,\sigma ,\tau } \right),$ z0 и σ0 – начальные координаты центра импульса вдоль соответствующих осей, γ параметр обрезания для функции Бесселя, а функция Матьё имеет вид [18]:

(9)
$\begin{gathered} {\text{Jce}}\left( r \right) = \frac{{2\int\limits_0^{{{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 2}} \right. \kern-0em} 2}} {{\text{cos}}\left( {2\sqrt q {\text{ch}}\left( r \right){\text{cos}}\left( t \right)} \right){\text{c}}{{{\text{e}}}_{0}}\left( {t,q} \right)dt} }}{{\pi {\text{c}}{{{\text{e}}}_{0}}\left( {0,q} \right)}}, \\ {\text{с}}{{{\text{e}}}_{0}}\left( {z,q} \right) = \frac{1}{{\sqrt 2 }}\left( {1 - \frac{q}{2}{\text{cos}}\left( {2z} \right) + {{q}^{2}}\left( {\frac{{{\text{cos}}\left( {4z} \right) - 2}}{{32}}} \right) - } \right. \\ \left. { - \,\,{{q}^{3}}\left( {\frac{{{\text{cos}}\left( {6z} \right) - 99{\text{cos}}\left( {2z} \right)}}{{1152}}} \right) + ...} \right). \\ \end{gathered} $

Эволюционная картина для трехмерного импульса при его распространении по образцу приведена на рис. 1.

Рис. 1.

Эволюция импульса Бесселя (а–в) и Матьё (г–е): t = 0 (a, г), 7 · 10–14 (б, д), t = 2 · 10–13 c (в, е). Единица по осям r, z, τ и σ соответствует 2 · 10–5 м. I0 – максимальная интенсивность в начальный момент времени.

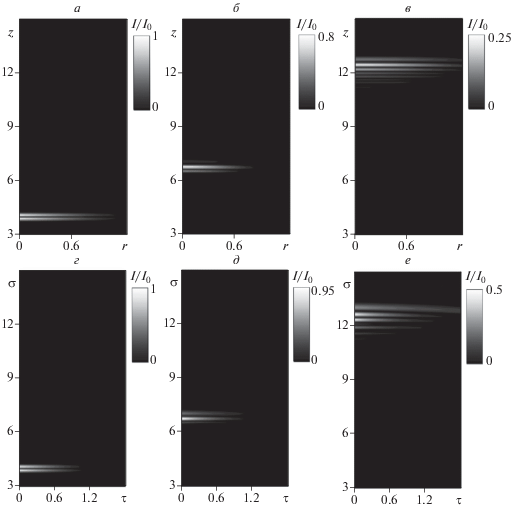
Из рис. 1 видно, что импульсы распространяется по образцу, оставаясь локализованным. Стоит отметить их уширение с течением времени.

Влияние параметров функции Бесселя (γr) и Матьё (γτ) на распространение импульса продемонстрировано на рис. 2 и 3. Видно, что, задавая соответствующим образом начальные условия для импульса Бесселя (рис. 2а) можно управлять формой предельно короткого импульса при распространении в массиве УНТ. Это дает перспективы для практических приложений, связанных с длительностью ПКИ. Аналогичным образом обстоит дело и с начальными условиями в виде функций Матьё (рис. 2б). Управляя начальными условиями, можно задавать ту или иную поперечную структуру импульса, сосредотачивая энергию или в центре, или в “крыльях”.

Рис. 2.

Зависимость напряженности электрического поля импульса: t = 2 · 10–13 с. Импульс Бесселя (продольные срезы при r = 0): кривая 1 соответствует γr = 0.01; кривая 2 – γr = 0.1; кривая 3 – γr = 0.2 (в единицах r) (а). Импульс Матьё при фиксированном значении координаты σ, для которой наблюдается максимум поля: кривая 1 соответствует γτ = 0.02; кривая 2 – γτ = 0.01; кривая 3 – γτ = 0.005 (в единицах τ) (б). Единица по осям z и τ соответствует 2 · 10–5 м. Im – максимальная интенсивность для указанных параметров.

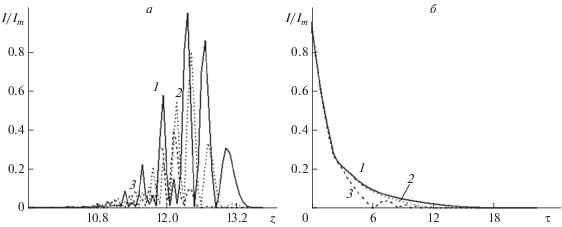
Рис. 3.

Зависимость напряженности электрического поля импульса: Бесселя (а) и Матьё (б) при t = 2 · 10–13 с. Представлены продольные срезы при нулевом значении поперечной координаты: кривая 1 соответствует R = Q = –D = –0.1; кривая 2 – R = Q = –D = –1 (в единицах интеграла перескока 2.7 эВ). Единица по осям z и σ соответствует 2 · 10–5 м. Im – максимальная интенсивность для указанных параметров.

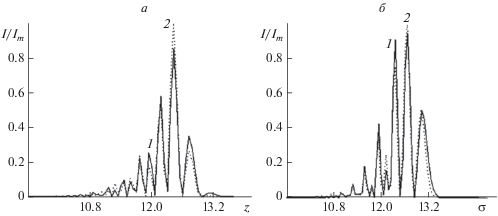
Влияние параметров примеси на импульс представлено на рис. 3. Отметим, что наиболее сильно примеси влияют на распространение импульса Бесселевой формы и изменяют его амплитуду сильнее, чем в случае импульса Матьё. Это, в свою очередь, позволяет управлять формой импульсов путем допирования, и контролировать степень допирования по форме ПКИ. Причина же изменения формы импульсов связана с изменением закона дисперсии для электронов в УНТ.

ЗАКЛЮЧЕНИЕ

Имеет место возможность локализованного распространения импульса, обусловленная балансом двух процессов – дисперсии и нелинейности. Дисперсионное уширение импульсов в ходе распространения можно компенсировать подбором соответствующих параметров начальной формы импульса (ширины, параметра функции Матьё q), с помощью которых возможно управление формой предельно короткого оптического импульса и его локализацией. Выявлено, что за счет введения примеси можно контролировать амплитуду предельно короткого импульса. Наибольшее влияние параметры примеси оказывают на импульсы с поперечным сечением Бесселя.

Авторы выражают благодарность Министерству науки и высшего образования РФ за поддержку в рамках государственного задания (численное моделирование; проект № 0633-2020-0003).

Список литературы

  1. Recami E. // Physica A. 1998. V. 252. P. 586.

  2. Ziolkowski R.W. // Phys. Rev. A. 1989. V. 39. P. 2005.

  3. Zamboni-Rached M., Recami E., Hernández-Figu-eroa H.E. // Eur. Phys. J. D. 2002. V. 21. P. 217.

  4. Durnin J., Miceli J.J., Eberly J.H. // Phys. Rev. Lett. 1987. V. 58. P. 1499.

  5. Gutiérrez-Vega J.C., Iturbe-Castillo M.D., Chávez-Cerda S. // Opt. Lett. 2000. V. 25. P. 1493.

  6. Mihalache D. // Rom. Rep. Phys. 2021. V. 73. Art. No. 403.

  7. Saito R., Dresselhaus M.S. Optical properties of carbon nanotubes. Amsterdam: Elsevier, 2014. P. 77.

  8. Белоненко М.Б., Лебедев Н.Г., Попов А.С. // Письма в ЖЭТФ. Т. 91. № 9. С. 506; Belonenko M.B., Lebedev N.G., Popov A.S. // JETP Lett. 2010. V. 91. No. 9. P. 461.

  9. Belonenko M.B., Dvuzhilov I.S., Nevzorova Yu.V. et al. // JNEP. 2016. V. 8. No. 3. Art. No. 03042.

  10. Konobeeva N.N., Belonenko M.B. // Mod. Phys. Lett. B. 2017. V. 31. No. 2. Art. No. 1750005.

  11. Белоненко М.Б., Мостовая Е.И. // Опт. и спектроск. 2019. Т. 126. С. 563; Belonenko M.B., Mostovaya E.I. // Opt. Spectrosс. 2019. V. 126. P. 482.

  12. Gutiérrez-Vega J.C., Iturbe-Castillo M.D., Ramı́rez G.A. // Opt. Comm. 2001. V. 195. P. 35.

  13. Zhukov A.V., Bouffanais R., Fedorov E.G. et al. // J. Appl. Phys. 2013. V. 114. Art. No. 143106.

  14. Zhukov A.V., Bouffanais R., Konobeeva N.N. et al. // EPL. 2014. V. 106. Art. No. 37005.

  15. Елецкий А.В. // УФН. 1997. Т. 167. № 9. С. 945; Eletskii A.V. // Phys. Usp. 1997. V. 40. P. 899.

  16. Dresselhaus M.S., Dresselhaus G., Eklund P.C. Science of fullerenes and carbon nanotubes. San Diego: Academic Press, 1996. 965 p.

  17. Belonenko M.B, Demushkina E.V., Lebedev N.G. // J. Russ. Laser Res. 2006. V. 27. P. 457.

  18. Абрамовиц М., Стиган И. Справочник по специальным функциям, с формулами, графиками и математическими таблицами. М.: Наука, 1979. 832 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал