Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 142-147
Влияние температуры атмосферы на формирование осеннего термобара
Н. С. Блохина 1, *, В. А. Борзых 1
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Московский государственный университет имени М.В. Ломоносова”, физический факультет
Москва, Россия
* E-mail: blokhinans@gmail.com
Поступила в редакцию 24.08.2021
После доработки 06.09.2021
Принята к публикации 22.09.2021
- EDN: EZQEVB
- DOI: 10.31857/S0367676522010070
Аннотация
С помощью математического моделирования исследуется развитие осеннего термобара в водоеме при различных термических состояниях атмосферы. Установлена связь между скоростью его перемещения и температурой атмосферы. Обнаружены две фазы развития термобара (медленная и быстрая). Выявлен эффект расхождения между зоной опускания вихрей и месторасположением изотермы 4°C на поверхности водоема.
ВВЕДЕНИЕ
Температура воды как одна из физических характеристик определяет распределение плотности в водоемах. Поэтому она играет важнейшую роль в вертикальной устойчивости водных масс, возникновении циркуляций и течений. Формирование термического и динамического режима озера связано с различными явлениями. К их числу относится термобар (термический бар, ТБ), возникающий весной и осенью в пресных и солоноватых водоемах (S ≤ 24‰) средних широт при нагревании (весной) или охлаждении (осенью) воды у берега до температуры максимальной плотности (Тmах). Для пресной воды Тmах = 4°С. Термобар представляет собой фронтальный раздел с температурой максимальной плотности от поверхности до дна, где сходятся и опускаются ко дну водоема прибрежные и глубинные воды, образуя справа и слева от него конвективные вихревые структуры. Происходит разделение водоема на две изолированные области с разными видами вертикальной стратификации температуры, что препятствует формированию единой циркуляции в нем и, следовательно, перемешиванию вод по всему водному объекту. По мере весеннего прогрева (осеннего охлаждения) водоема термобар перемещается от берега к его центру и исчезает весной при достижении поверхностных вод температуры большей 4°С, а осенью – меньшей 4°С. Время существования фронтальной зоны может составлять от нескольких дней, до нескольких месяцев в зависимости от размеров озера. Ограничивая обмен между глубоководной и прибрежной областями в водоеме, ТБ влияет на его термодинамические, биологические и экологическое процессы [1]. В связи с этим исследование явления ТБ представляет большой научный и практический интерес.
Особенности охлаждения (прогрева) Женевского озера, связанные с появлением в нем осеннего (весеннего) термобара, впервые качественно описал Ф.А. Форель [2]. Только в середине XX века А.И. Тихомиров продолжил детальное изучение ТБ и дал физическое объяснение механизма формирования и развития этого явления [3, 4]. В дальнейшем в подавляющем большинстве работ, посвященных изучению термобара, исследуются термогидродинамические процессы в водоемах в весенне-летний период, так как в это время года легче проводить натурные наблюдения, а в лабораториях создавать условия для развития весеннего ТБ. Работ по изучению осеннего ТБ единицы. В природных условиях особенности развития термического фронта осенью исследовались в работах E.C. Кармака и Д.М. Фармера [5], Г.К. Роджерса [6], П.П. Шерстянкина и др. [7], Н.Ю. Демченко и др. [8]. В лабораторных условиях осенний ТБ изучался в работах Дж. Эллиотом [9, 10], И.П. Чубаренко и Н.Ю. Демченко [11]. Теоретические исследования в этом направлении проводились И.П. Чубаренко и К. Хаттером [12], Б.О. Цыденовым и др. [13–15].
В настоящей работе с помощью математического моделирования исследуются процессы формирования и развития осеннего термобара и сопутствующих ему течений в пресном водоеме при различных термических состояниях атмосферы.
ФИЗИКО-МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Рассматривается движение вязкой несжимаемой жидкости, находящейся в двумерной области (соответствующей половине водоема) шириной L (по поверхности) и глубиной H с наклонной правой границей (см. рис. 1). Решение двумерной задачи допустимо, так как в природных условиях термобар перемещается к центу водоема параллельно прибрежной области, в направлении которой движение однородно. Задача решается в прямоугольной системе координат (O; X2; Х3). За начало отсчета принят левый нижний угол. Ось OX2 направлена перпендикулярно фронту термобара, ось ОХ3 – вертикально вверх. Математическая модель движения жидкости в водоеме построена на основе нелинейной системы уравнений Навье–Стокса в приближении Буссинеска, уравнении переноса тепла и неразрывности, записанных в переменных функции тока (ψ) и вихря (φ) [16–18]. Аномальная зависимость плотности пресной воды от температуры в районе 4°С учитывается в уравнении состояния (1).
(1)
$\rho \left( Т \right) = {{\rho }_{о}}\left( {4^\circ {\text{C}}} \right) - {{\rho }_{о}}\left( {4^\circ {\text{C}}} \right){{\gamma }}{{\left( {T - 4^\circ {\text{C}}} \right)}^{2}}.$Рис. 1.
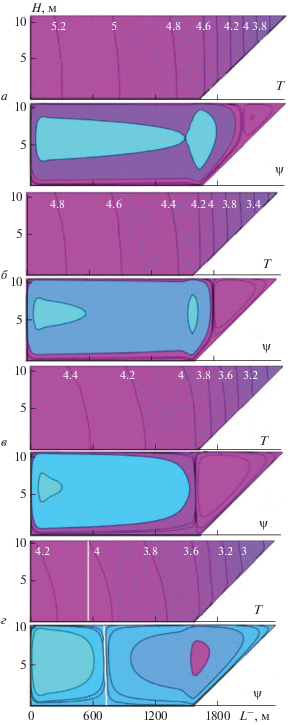
Поля температуры (T) и функции тока (ψ) через t = 83 ч после начала счета для температуры атмосферы: $~{{T}_{a}}$ = 4 (а), 0 (б), –4 (в); –8°C (г).
Здесь ρ и ρо – плотность воды при температуре T и 4°С соответственно, γ = 85 ∙ 10–7 град–2.
В безразмерном виде система уравнений и уравнение замыкания примут вид:
(2)
$\begin{gathered} \frac{{\partial {{\varphi }}}}{{\partial t}} + \left( {\frac{{\partial {{\psi }}}}{{\partial {{x}_{3}}}}\frac{{\partial {{\varphi }}}}{{\partial {{x}_{2}}}} - \frac{{\partial {{\psi }}}}{{\partial {{x}_{2}}}}\frac{{\partial {{\varphi }}}}{{\partial {{x}_{3}}}}} \right) = {{\mu }}\left( {\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial x_{2}^{2}}} + \frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial x_{3}^{2}}}} \right) - \\ - \,\,2\left( {T - {{T}_{4}}} \right)\frac{{\partial T}}{{\partial {{x}_{2}}}}, \\ \end{gathered} $(3)
$\frac{{\partial T}}{{~\partial t}} + \left( {\frac{{\partial {{\psi }}}}{{\partial {{x}_{3}}}}\frac{{\partial T}}{{\partial {{x}_{2}}}} - \frac{{\partial {{\psi }}}}{{\partial {{x}_{2}}}}\frac{{\partial T}}{{\partial {{x}_{3}}}}} \right) = {{\mu }}\left( {\frac{{{{\partial }^{2}}T}}{{\partial x_{2}^{2}}} + \frac{{{{\partial }^{2}}T}}{{\partial x_{3}^{2}}}} \right),$(5)
$\begin{gathered} {{{{\mu }}}^{2}} = \frac{{{{c}^{3}}}}{s} \times \\ \times \,\,\int\limits_s {\left[ {4{{{\left( {\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{x}_{2}}\partial {{x}_{3}}}}} \right)}}^{2}} + {{{\left( {\frac{{{{\partial }^{2}}{{\psi }}}}{{\partial x_{3}^{2}}} - \frac{{{{\partial }^{2}}{{\psi }}}}{{\partial x_{2}^{2}}}} \right)}}^{2}} - \left( {T - {{T}_{4}}} \right)\frac{{\partial T}}{{\partial {{x}_{3}}}}} \right]} ds. \\ \end{gathered} $Граничные условия для системы уравнений (2)–(4) задаются следующие.
На дне водоема и правой наклонной боковой границе – условия непроницаемости и прилипания для скорости и отсутствия теплового потока:
(6)
$\begin{gathered} \frac{{\partial {{\psi }}}}{{~\partial {{x}_{2}}}} = \frac{{{{\partial }^{2}}{{\psi }}}}{{\partial x_{3}^{2}}} = 0,\,\,\,\frac{{\partial T}}{{\partial {{x}_{3}}}} = 0 \\ {\text{и}}\,\,\,\frac{{\partial {{\psi }}}}{{\partial n}} = \frac{{{{\partial }^{2}}{{\psi }}}}{{\partial {{n}^{2}}}} = 0,\,\,\,\frac{{\partial T}}{{\partial n}} = 0, \\ \end{gathered} $На левой границе условие симметрии:
На верхней границе – условие “свободной” поверхности для скорости и тепловой поток:
(8)
$\frac{{\partial {{\psi }}}}{{\partial {{x}_{2}}}} = 0,\,\,\,\,{{\varphi }} = \frac{{{{\partial }^{2}}{{\psi }}}}{{\partial x_{3}^{2}}} = 0,\,\,\,\, - {{\mu }}\frac{{\partial T}}{{\partial {{x}_{3}}}} = {{Q}^{b}}.$ПАРАМЕТРЫ ЗАДАЧИ
Расчеты проводили в водоеме глубиной Н = = 10 м и шириной L = 2400 м (половина водоема). Температура атмосферы Ta изменялась от 4 до ‒10°C с шагом –2°C; относительная влажность воздуха принимала значение f = 80%. Поток солнечной радиации QR, поступающий на границу раздела между водоемом–атмосферой задавался равным 25 Вт · м–2, что соответствует его среднемесячному значению поздней осенью на широтах Санкт-Петербурга. Начальные поля распределения температуры (T) для всех вариантов расчета были заданы одинаковыми и приблизительно соответствовали распределению температуры в водоеме осенью. Поля функции тока (ψ) и вихря (φ) задавались нулевыми.
Система уравнений (2)–(4), уравнение замыкания (5) совместно с граничными условиями (6)–(9) решались численно с использованием явной конечно-разностной схемы на сетке 26 × 75 с размерным шагом по вертикали и горизонтали 0.4 и 32 м соответственно.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ
В результате расчетов были получены поля температуры (T), функции тока (ψ), скоростей течения и др. для разных значений температуры атмосферы. Для Та = 4, 0, –4, –8°C через t = 83 ч после начала расчетов поля T и ψ представлены на рис. 1. При всех заданных тепловых состояниях атмосферы у берега возникает термобар. По мере охлаждения прибрежной области, происходит перемещение термического фронта к центру водоема, что сопровождается увеличением наклона изотерм в ту же сторону. Справа и слева от ТБ формируются конвективные вихри, сходящиеся в зоне фронта. При этом усиливается прибрежный циклонический вихрь, способствующий дополнительному охлаждению глубинной области водоема за счет переноса к его центру более холодной воды от берега. Чем ниже температура атмосферы, тем быстрее ТБ перемещается к центральной части водоема. Если в случае Та = 4°C термобар находится в 416 м от берега, то при Та = –8°C он переместится на 1824 м. Время “жизни” (tж) фронтального раздела в водоеме в первой ситуации tж = 97 ч, а во второй в 2.6 раз больше (tж = 249 ч). После охлаждения поверхностных вод до температуры меньшей 4°C, термобар исчезает, и весь водоем охватывает единая циклоническая циркуляция.
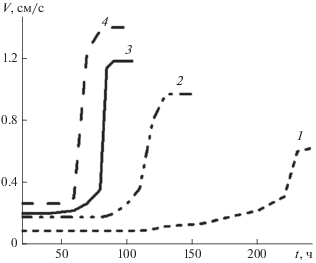
По графикам на рис. 2 можно проследить за изменением положения термобара со временем для различных значений температуры атмосферы. Каждая кривая имеет точку изгиба, начиная с которой расстояние между ТБ и берегом увеличивается быстрее со временем, чем до этой точки. Наблюдается две фазы скоростей перемещения термического бара. Это хорошо видно на рис. 3, где представлены графики зависимости скорости (V) перемещения фронтального раздела в зависимости от времени охлаждения водоема (t) для разных значений температур атмосферы. Первая медленная фаза существует, пока фронтальная зона не достигает конца наклонного берега. В этот период времени скорость перемещения ТБ (V1) практически постоянная для каждого значения температуры атмосферы. При этом, чем ниже ${{T}_{a}},$ тем быстрее перемещается ТБ. В зависимости от ${{T}_{a}}$ она изменяется от V1 = 0.1 см/с (для ${{T}_{a}}$ = 4°C) до V1 = 0.27 см/с (для ${{T}_{a}}$ = –8°C). Во втором случае скорость V2 увеличивается линейным образом с увеличением времени охлаждения водоема и тем больше, тем холоднее атмосфера. Характерные значения скоростей движения ТБ во второй фазе изменяются от V2 = 0.59 см/с (для ${{T}_{a}}$ = 4°C) до V2 = 1.29 см/с (для ${{T}_{a}}$ = –8°C). Здесь для каждого значения ${{T}_{a}}$ наблюдается своя линейная зависимость V2 от времени t. Полученные скорости перемещения осеннего термобара, близки к данным натурных наблюдений в озерах Канады (V = = 0.58 см/c) [5].
Рис. 2.
Зависимости положения термобара на поверхности водоема от времени (t) для температуры атмосферы: $~{{T}_{a}}$ = 4 (1), 0 (2), –4 (3); –8°C (4). Начало отсчета по оси ординат от берега.
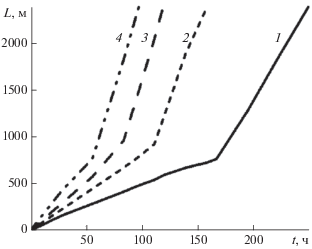
Рис. 3.
Скорости перемещения фронтального раздела (V) в зависимости от времени охлаждения водоема (t) для температуры атмосферы: $~{{T}_{a}}$ = 4 (1), 0 (2), –4 (3); ‒8°C (4). Начало отсчета по оси ординат от берега.
Объяснить существование двух фаз, определяющих разные скорости перемещения фронтальной зоны, можно следующим образом. Критерием конвективной неустойчивости водных масс является число Грасгофа Gr. Для квадратичной зависимости плотности воды от температуры оно получено в работе [21]:
здесь g – ускорение свободного падения, ${{\gamma }}$ – коэффициент в формуле (1), ΔТ – разница температур между дном и поверхностью водоема, h – глубина водоема, ν – кинематическая вязкость жидкости.Чем больше число Грасгофа, тем менее устойчив слой жидкости. В моменты времени, когда прибрежный вихрь находится над наклонным берегом (рис. 1а, 1б), глубина водоема h1 в этом месте меньше, чем в области глубинного вихря (h2). Например, для случая на рис. 1б h1 ≈ 5 м, а h2 = 10 м. Если полагать, что перепады температуры ΔТ в областях конвективных вихрей не сильно отличаются, то основной вклад в конвективную неустойчивость водной массы справа и слева от термобара вносят параметры h1 и h2. Число Грасгофа для первого случая Gr1 ~ 125, а для второго Gr2 ~ 103. Таким образом, в начальный момент времени в водоеме существует мощный глубинный вихрь, препятствующий перемещению воды от берега. По мере остывания поверхности водоема и перемещения ТБ к его центру, увеличивается вертикальный размер h1 и, следовательно, интенсивность прибрежной циркуляции, что приводит к увеличению скорости движения фронтальной зоны. Две фазы скоростей перемещения весеннего ТБ наблюдались в лабораторных экспериментах в работах [5, 11, 22].
Отметим, что, не доходя примерно 60 м до центра водоема, скорости движения фронтального раздела для каждого теплового состояния атмосферы замедляются и становятся постоянными (рис. 3).
В ходе исследования был обнаружен эффект расхождения положения изотермы 4°C на поверхности водоема и зоны опускания водных масс, что расходится с классическим представлением о термобаре как о зоне схождения вихревых структур в области расположения изотермы 4°C (от поверхности до дна). Это хорошо видно, например, на риc. 1г, (Та = = –8°C), где вертикальными линиям обозначены эти области. Зависимости положения изотермы Т = 4°C на поверхности водоема (кривая 1) и зоны схождения вихрей (кривая 2) от термического состояния атмосферы представлены на рис. 4. При уменьшении температуры воздуха прослеживается большее расхождение этих зон. При этом область опускания водных масс отстает от расположения изотермы 4°C. Этот эффект также хорошо прослеживается по мере удаления термобара от берега при одном и том же значении Та (нет графиков). Чем холоднее воздух или чем дольше охлаждается акватория водоема, тем быстрее термический бар продвигается к его центру, опережая область опускания вихревых структур. В водоеме наблюдается горизонтальная термическая неоднородность, и как следствие градиент температуры между теплыми глубинными и более холодными прибрежными водами. Наличие градиента температуры создает адвективный поток тепла, который усиливает глубинный антициклонический вихрь, увеличивая горизонтальную скорость движения жидкости в нем, и замедляет прибрежную циркуляцию. Так при Та = –8°С горизонтальная скорость течения воды в антициклонической циркуляции на поверхности воды вблизи фронта ТБ равна 0.29 см/c, а во встречном циклоническом вихре – 0.2 см/c. При увеличении температуры воздуха и уменьшении времени охлаждения водоема разница в горизонтальных скоростях встречных вихрей уменьшается, что сокращает ширину зоны расхождения между изотермой 4°С и конвективными вихрями.
Рис. 4.
Зависимость положения изотермы Т = 4°C на поверхности воды (1) и зоны схождения вихрей (2) от температуры атмосферы через t = 83 ч после начала счета. Начало отсчета по оси ординат от берега.
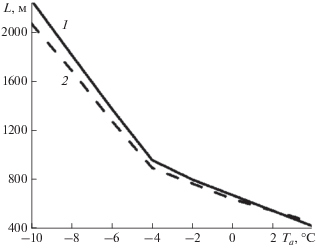
Аналогичный эффект на поверхности Ладожского озера в восточной его части наблюдали С.Г. Каретников и М.А. Науменко (по устному сообщению А.М. Науменко). Выход изотермы 4°С на поверхность водоема опережал область схождения вихрей на 8 км. При этом термобар находился дальше от берега (в 28 км). В теоретической работе [23] также обнаружен этот эффект. Автор связывает его с глубиной водоема и ветровым воздействием на его поверхность.
ЗАКЛЮЧЕНИЕ
В результате исследований было показано, что развитие термобара в пресных водоемах осенью существенным образом зависит от термического состояния атмосферы. При низких температурах воздуха время его “жизни” в водоеме может уменьшиться в несколько раз. Выявлено неравномерное распространение ТБ по мере охлаждения водоема при всех заданных значениях температуры атмосферы. Наблюдаются две фазы развития термического фронта со скоростями V1 и V2. Первая медленная фаза существует, пока фронт термобара не достигнет конца наклонного берега, после чего наступает вторая быстрая фаза. Скорость (V1) перемещения ТБ в первой фазе постоянна по времени и увеличивается при меньших значениях Та. Во второй фазе для каждого термического состояния атмосферы наблюдается своя линейная зависимость V2 от времени охлаждения водоема. При этом V2 тем больше, чем холоднее атмосфера. Не доходя примерно 60 м до центра водоема, скорость передвижения ТБ для каждого теплового состояния атмосферы замедляется и становится постоянной. Обнаружен эффект расхождения изотермы Т = 4°С в водоеме и зоны схождения вихрей, что не соответствует классическому представлению о термобаре.
Список литературы
Блохина Н.С., Показеев К.В. // Земля и Вселенная. 2015. № 6. С. 78.
Форель Ф.А. Руководство по озероведению. СПб., 1912. 196 с.
Тихомиров А.И. // Изв. ВГО. 1959. Т. 91. № 5. С. 424.
Тихомиров А.И. Термика крупных озер. Л.: Наука, 1982. 232 с.
Carmack E.C., Farmer D.M. // J. Mar. Res. 1982. V. 40. P. 85.
Rodgers G.K. // Proc. 9th Conf. Great Lakes Res. (Ann Arbor, 1966). P. 369.
Шерстянкин П.П., Иванов В.Г., Куимова Л.Н. и др. // Водн. ресурсы. 2007. Т. 34. №. 4. С. 439; Sherstyankin P.P., Ivanov V.G., Kuimova L.N. et al. // Water resources. 2007. V. 34. No. 4. P. 408.
Демченко Н.Ю., Чубаренко И.П. // Океанология. 2012. Т. 52. № 6. С. 790; Demchenko N.Y., Chubarenko I.P. // Oceanology. 2012. V. 52. No. 6. P. 728.
Elliott G.H. A laboratory and mathematical study of the 'thermal bar'. PhD thesis, Vancouver: Inst. Oceanogr., Univ. British Columbia, 1970. 99 p.
Elliott G.H., Elliott J.A. // Proc. 13th Conf. Great Lakes Res. (New York, 1970). P. 413.
Чубаренко И.П., Демченко Н.Ю. // Океанология. 2008. Т. 3. № 48. С. 356; Chubarenko I.P., Demchenko N.Yu. // Oceanology. 2008. V. 48. No. 3. P. 327.
Chubarenko I., Hutter K. // J. Limnol. 2005. V. 64. No. 1. P. 31.
Цыденов Б.О. // Вестн. Моск. ун-та. Сер. 3. Физ. и астрон. 2018. № 4. С. 52; Tsydenov B.O. // Moscow Univ. Phys. Bull. 2018. V. 73. No. 4. P. 435.
Цыденов Б.О. // Вестн. Моск. ун-та. Сер. 3. Физ. и астрон. 2019. № 1. С. 64; Tsydenov B.O. // Moscow Univ. Phys. Bull. 2019. V. 74. No. 1. P. 70.
Tsydenov B.O. // J. Mar. Syst. 2018. V. 179. P. 1.
Блохина Н.С., Орданович А.Е., Савельева О.С. // Водн. ресурсы. 2001. Т. 28. № 2. С. 224; Blokhina N.S., Ordanovich A.E., Savel’eva O.S. // Water Res. 2001. V. 28. P. 201.
Блохина Н.С., Овчинникова А.В., Орданович А.Е. // Вестн. Моск. ун-та. Сер. 3. Физ. и астрон. 2002. № 2. С. 60; Blokhina N.S., Ovchinnikova A.V., Ordanovich A.E. // Moscow Univ. Phys. Bull. V. 57. No. 2. P. 73.
Блохина Н.С. // Изв. РАН. Сер. физ. 2017. Т. 81. № 1. С. 106; Blokhina N.S. // Bull. Russ. Acad. Sci. Phys. 2017. V. 81. No. 1. P. 96.
Хргиан А.Х. Физика атмосферы. Л.: Гидромет. изд-во, 1969. 647 с.
Гилл А. Динамика атмосферы и океана. Т. 1. М.: Мир, 1986. 397 с.
Блохин А.С., Блохина Н.С. // Докл. АН СССР. 1970. Т. 193. С. 805.
Соловьев Д.А., Блохина Н.С., Орданович А.Е. // Вестн. Моск. ун-та. Сер. 3. Физ. и астрон. 2007. № 5. С. 65; Solov’ev D.A., Blokhina N.S., Ordanovich A.E. // Moscow Univ. Phys. Bull. 2007. V. 62. No. 5. Р. 332.
Блохина Н.С. // Вестн. Моск. ун-та. Сер. 3. Физ. и астрон. 2015. № 4. С. 102; Blokhina N.S. // Moscow Univ. Phys. Bull. 2015. V. 70. P. 319.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


