1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 1, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 58-62

Проводимость однослойных углеродных нанотрубок полупроводникового типа с учетом ионизации примесных центров

С. Ю. Глазов 1, 2, *, Н. Е. Мещерякова 2, И. А. Подгорная 1, 2

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Волгоградский государственный социально-педагогический университет”
Волгоград, Россия

2 Федеральное государственное бюджетное образовательное учреждение высшего образования “Волгоградский государственный медицинский университет”
Волгоград, Россия

* E-mail: ser-glazov@yandex.ru

Поступила в редакцию 24.08.2021
После доработки 06.09.2021
Принята к публикации 22.09.2021

Полный текст (PDF)

Аннотация

Исследована зависимость плотности тока в однослойной углеродной нанотрубке полупроводникового типа от характеристик приложенных статического и переменного электрических полей с учетом ионизации примесных центров. Для расчета тока использовано решение кинетического уравнения Больцмана с модельным интегралом столкновений Батнагара–Гросса–Крука при учете темпа генерации и рекомбинации.

ВВЕДЕНИЕ

В последнее время внимание исследователей сосредотачивается на изучении графеновых структур и, в частности, углеродных нанотрубок (УНТ). Исследованию проводимости УНТ посвящено достаточно большое количество работ [1–5]. В [3] изучена проводимость УНТ различных типов в присутствии постоянного электрического поля, получены вольт-амперные характеристики, выявлены участки дифференциальной отрицательной проводимости. В [5, 6] исследовано влияние переменного электрического поля на проводимость и генерацию высших гармоник тока вертикально выровненного массива однослойных УНТ полупроводникового типа, находящегося в постоянном электрическом поле, и выявлен эффект абсолютной отрицательной проводимости.

Особый интерес вызывают структуры с контролируемыми примесями, в которых появляется возможность, задавая параметры примесей (концентрацию, глубину залегания), управлять их характеристиками [7–10]. Транспортные свойства УНТ существенно различаются в зависимости от структуры и условий синтеза (наличия примесей и дефектов), поэтому экспериментальные значения данных свойств варьируются в больших пределах. Развитие наноинженерии открывает возможность создания УНТ с определенными примесями, вплоть до “чистых” образцов [11].

В этой связи представляется актуальным исследовать зависимость плотности тока в однослойных УНТ от характеристик приложенных статического и переменного электрических полей с учетом ионизации примесных центров.

ОСНОВНЫЕ УРАВНЕНИЯ

Энергетический спектр носителей заряда в УНТ типа zigzag (m,0) в приближении сильной связи имеет вид [3]

(1)
$\varepsilon (\vec {p}) = \pm \gamma \sqrt {1 + 4\cos (a{{p}_{z}})\cos \left( {\frac{{\pi s}}{m}} \right) + 4{{{\cos }}^{2}}\left( {\frac{{\pi s}}{m}} \right)} ,$
где квазиимпульс $\vec {p}$ задается как $({{p}_{z}},s),$ γ ≈ 2.7 эВ, $a = {{3b} \mathord{\left/ {\vphantom {{3b} {2\hbar }}} \right. \kern-0em} {2\hbar }},$ b = 0.142 нм − расстояние между соседними атомами углерода, s = 1, 2 … m, разные знаки относятся к зоне проводимости и валентной зоне. Ограничимся случаем полупроводниковых УНТ типа zigzag (3p – 1, 0) и (3p + 1, 0), где p – натуральное число.

Скорость движения носителей заряда вдоль оси нанотрубки

(2)
$\begin{gathered} {{\upsilon }_{z}}\left( {{{p}_{z}},s} \right) = \\ = \mp \gamma \frac{{2a\sin \left( {a{{p}_{z}}} \right)\cos \left( {\frac{{\pi s}}{m}} \right)}}{{\sqrt {1 + 4\cos \left( {a{{p}_{z}}} \right)\cos \left( {\frac{{\pi s}}{m}} \right) + 4{{{\cos }}^{2}}\left( {\frac{{\pi s}}{m}} \right)} }}. \\ \end{gathered} $

Приложенные постоянное и переменное электрические поля поляризованы вдоль оси нанотрубки $\vec {E} = \left( {0,0,{{E}_{1}} + {{E}_{0}}\cos \omega t} \right)$ – суммарная напряженность электрического поля, E1 – модуль напряженности постоянного электрического поля, E0 и ω – амплитуда и частота переменного электрического поля.

Плотность тока jz текущего вдоль оси z определяется по формуле

(3)
${{j}_{z}} = - e\sum\limits_{\vec {p}} {{{\upsilon }_{z}}(\vec {p})f(\vec {p})} ,$
где е – заряд электрона, $f(\vec {p})$ – неравновесная функция распределения носителей, которая может быть найдена из уравнения Больцмана с модельным интегралом столкновений Батнагара–Гросса–Крука [10].

После разложения скорости носителей в ряд Фурье по pz, и с учетом найденной неравновесной функции распределения для невырожденного электронного газа, после усреднения по времени определяем постоянную составляющую плотности тока

(4)
${{j}_{z}} = {{j}_{0}}{{B}_{{ion}}}\sum\limits_{s = 1}^m {\sum\limits_{n = 1}^\infty {{{A}_{{sn}}}{{C}_{{sn}}}} \sum\limits_{k = - \infty }^\infty {J_{k}^{2}(n\alpha )\sin {{\varphi }_{{kn}}}\cos {{\varphi }_{{kn}}}} } ,$
где ${{j}_{0}} = ea{{n}_{0}}\gamma ,$ n0 – концентрация электронов в зоне проводимости, ${{B}_{{ion}}} = 1$ + $\frac{N}{{{{n}_{0}}}}$$\frac{{\exp ( - 2\operatorname{Im} S)}}{{{{\nu }_{r}}\operatorname{Im} {{t}_{0}} + \exp ( - 2\operatorname{Im} S)}},$ N – концентрация примесей в УНТ, S – классическое действие, набираемое электроном при подбарьерном движении, t0 – время начала туннелирования, ν – характерная частота релаксации, νr – частота рекомбинации, Jn(x) – функция Бесселя 1-го рода n-го порядка, $\sin {{\varphi }_{{kn}}}$ = = $\frac{\nu }{{\sqrt {{{\nu }^{2}} + {{{(n\Omega + k\omega )}}^{2}}} }},$ $\Omega = e{{E}_{1}}a,$ $\alpha = {{e{{E}_{0}}a} \mathord{\left/ {\vphantom {{e{{E}_{0}}a} \omega }} \right. \kern-0em} \omega },$ ${{A}_{{sn}}} = \frac{2}{{\pi C}}$$\int_{ - {{\pi }}}^{{\pi }} {\frac{{\sin z\cos \left( {{{\pi s} \mathord{\left/ {\vphantom {{\pi s} m}} \right. \kern-0em} m}} \right)\sin nz}}{{\sqrt {1 + 4\cos z\cos ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} m}} \right. \kern-0em} m}) + 4{{{\cos }}^{2}}\left( {{{\pi s} \mathord{\left/ {\vphantom {{\pi s} m}} \right. \kern-0em} m}} \right)} }}} dz,$ $\delta = {\gamma \mathord{\left/ {\vphantom {\gamma {{{k}_{{\text{Б}}}}T}}} \right. \kern-0em} {{{k}_{{\text{Б}}}}T}},$

${{C}_{{sn}}} = \int\limits_{ - {{\pi }}}^{{\pi }} {\cos (na{{p}_{z}})} \exp ( - \delta \,\sqrt {1 + 4\cos a{{p}_{z}}\cos ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} m}} \right. \kern-0em} m}) + 4{{{\cos }}^{2}}({{\pi s} \mathord{\left/ {\vphantom {{\pi s} m}} \right. \kern-0em} m})} )d{{p}_{z}},$
$С = \sum\limits_s {\int {\exp [ - \delta \sqrt {1 + 4\cos a{{p}_{z}}\cos ({{\pi s} \mathord{\left/ {\vphantom {{\pi s} m}} \right. \kern-0em} m}) + 4{{{\cos }}^{2}}({{\pi s} \mathord{\left/ {\vphantom {{\pi s} m}} \right. \kern-0em} m})} ]d{{p}_{z}}} } .$

Используемый в данной работе квазиклассический метод расчета плотности тока применялся ранее для описания проводимости в приближении постоянного времени релаксации в идеальных (беспримесных) графеновых структурах [5, 12, 13].

Учет влияния ионизации примесей на проводимость УНТ проведен с использованием кинетического уравнения Больцмана с модельным интегралом столкновений Батнагара–Гросса–Крука при учете темпа генерации и рекомбинации [10]. В случае динамического равновесия концентрация носителей в зоне проводимости в присутствии внешних электрических полей равна n0Bion и определяется через вероятность ионизации примесей, рассчитанной с использованием метода мнимого времени [14, 15]. В случае совместного влияния статического и переменного электрических полей, поляризованных вдоль оси нанотрубки, выражение для мнимой части классического действия, которое набирает частица при подбарьерном движении, задается формулой

(5)
$\operatorname{Im} S = \int\limits_0^{{{{{\tau }}}_{{\text{0}}}}} {\left\{ {\gamma \sqrt {1 + 4{\text{ch}}\left( {\Omega t + \alpha {\text{sh}}(\omega t)} \right)\cos {{х}_{0}}\cos {{y}_{0}} + 4{{{\cos }}^{2}}{{y}_{0}}} + (\upsilon - \Delta )} \right\}} dt,$
где υ – глубина залегания примеси, Δ – полуширина запрещенной зоны, x0 и y0 – безразмерные компоненты квазиимпульса электрона, которые соответствуют минимальной энергии в зоне проводимости, а мнимая часть времени начала туннелирования τ0 определяется уравнением
(6)
$\Omega {{\tau }_{0}} + \alpha {\text{sh}}(\omega {{\tau }_{0}}) = \beta ,$
где β = arch({(Δ – υ)2/γ2 – 1 – 4cos2y0}/{4cosx0 cosy0}).

Ионизация приводит к увеличению концентрации носителей заряда в минизоне проводимости и, соответственно, к росту плотности тока.

ОСНОВНЫЕ РЕЗУЛЬТАТЫ

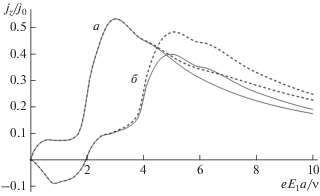
Анализ формулы (4), ввиду ее сложности, проводился численно. На рис. 1 показана зависимость постоянной составляющей плотности тока от напряженности постоянного электрического поля при фиксированных значениях частоты и амплитуды переменного электрического поля. Зависимость плотности тока от напряженности электрического поля имеет максимум, определяемый характерной частотой релаксации, участки с отрицательной дифференциальной и абсолютной отрицательной проводимостью [5, 16]. Сплошной линией представлен график, соответствующий “чистым” УНТ, пунктирной – с учетом ионизации примеси. Отклонение графика постоянной составляющей плотности тока для примесных УНТ от аналогичного графика для идеальных беспримесных начинается с некоторого значения напряженности постоянного электрического поля, когда возникает существенное увеличение концентрации носителей за счет ионизации примесных центров.

Рис. 1.

Зависимости постоянной составляющей плотности тока от напряженности постоянного электрического поля при ω/ν = 2; υ = 0.3Δ; а – ${{ae{{E}_{0}}} \mathord{\left/ {\vphantom {{ae{{E}_{0}}} \nu }} \right. \kern-0em} \nu } = 3;$ б – ${{ae{{E}_{0}}} \mathord{\left/ {\vphantom {{ae{{E}_{0}}} \nu }} \right. \kern-0em} \nu } = 5.$

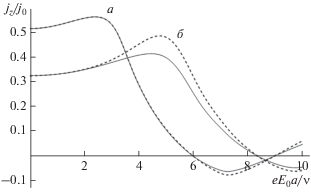
Зависимость постоянной составляющей плотности тока от амплитуды переменного электрического поля при его фиксированных значениях частоты и напряженности постоянного поля представлена на рис. 2. Зависимость имеет осциллирующий характер, на графиках также видны участки с отрицательной дифференциальной и абсолютной отрицательной проводимостью. Начиная с некоторого значения амплитуды напряженности переменного электрического поля, которое определяется напряженностью постоянного поля, частотой переменного поля, параметрами УНТ и примеси, происходит увеличение постоянной составляющей плотности тока в примесных по сравнению с “чистыми” УНТ.

Рис. 2.

Зависимости постоянной составляющей плотности тока от амплитуды переменного электрического поля при ω/ν = 2; υ = 0.3Δ; а – ${{ae{{E}_{1}}} \mathord{\left/ {\vphantom {{ae{{E}_{1}}} \nu }} \right. \kern-0em} \nu } = 3;$ б – ${{ae{{E}_{1}}} \mathord{\left/ {\vphantom {{ae{{E}_{1}}} \nu }} \right. \kern-0em} \nu } = 5.$

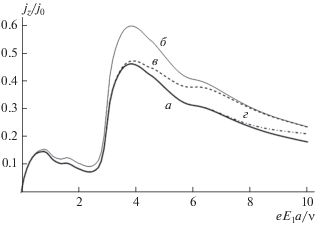
На рис. 3 представлена зависимость постоянной составляющей плотности тока от напряженности постоянного электрического поля при заданной частоте, амплитуде переменного электрического поля и разных значениях глубины залегания примесей. Начало роста тока и длительность процесса установления насыщения ионизации определяются глубиной залегания примеси и ее концентрацией. Подбор примеси заданной глубины приводит к возможности задания нужных проводящих свойств УНТ.

Рис. 3.

Зависимости постоянной составляющей плотности тока от напряженности постоянного электрического поля при ω/ν = 3; ${{ae{{E}_{0}}} \mathord{\left/ {\vphantom {{ae{{E}_{0}}} \nu }} \right. \kern-0em} \nu } = 4;$ а – без примесей; б – υ = 0.2Δ; в – υ = 0.3Δ; г – υ = 0.4Δ.

На основе результатов данного исследования возможно создание аппаратно-программного комплекса, анализирующего экспериментальные значения тока в зависимости от параметров электрических полей, предназначенного для определения глубины залегания и концентрации примеси.

При решении задачи, пренебрегалось межзонными переходами, что соответствует выполнению условия $\hbar \omega \ll 2\Delta $ (ω $ \ll $ 1015 с–1), и тепловыми забросами электронов с примеси в подзоны – kБT $ \ll $ υ (T $ \ll $ 2 ⋅ 103 К).

Сделаем численные оценки параметров, используемых при построении графиков на рис. 1–3: значения безразмерных напряженностей E при aeE/ν = 1 составляет 104 В/см, время релаксации τ = ν–1 = 3 ⋅ 10–12 с [3], температура 100 К. Представленные результаты приведены для УНТ типа zigzag (14,0), для которой Δ ≈ 1.32γ.

ЗАКЛЮЧЕНИЕ

Получено аналитическое выражение для нахождения плотности тока в однослойных УНТ в условиях воздействия статического и переменного электрических полей, поляризованных вдоль оси нанотрубки с учетом ионизации примесных центров. Наличие примесей приводит к возможности роста плотности тока за счет увеличения концентрации носителей заряда в минизоне проводимости вследствие ионизации примесных центров. Начало интенсивного роста тока и длительность процесса установления насыщения ионизации определяются параметрами примеси: глубиной залегания и концентрацией. Найденные зависимости плотности тока от параметров электрических полей могут быть использованы как в детекторах электромагнитного излучения, так и для уточнения глубины залегания примесных центров.

Список литературы

  1. Ebbesen T.W., Lezec H.J., Hiura H. et al. // Nature. 1996. V. 382. P. 54.

  2. Елецкий А.В. // УФН. 1997. Т. 167. № 9. С. 945; Eletskii A.V. // Phys. Usp. 1997. V. 40. P. 899.

  3. Максименко С.А., Слепян Г.Я. // Радиотехн. и электрон. 2002. Т. 47. № 3. С. 261; Maksimenko S.A., Slepyan G.Ya. // J. Commun. Technol. Electron. 2002. V. 47. No. 3. P. 235.

  4. Елецкий А.В. // УФН. 2009. Т. 179. № 3. С. 225; Eletskii A.V. // Phys. Usp. 2009. V. 52. P. 209.

  5. Белоненко М.Б., Глазов С.Ю., Мещерякова Н.Е. // ФТП. 2010. Т. 44. № 9. С. 1248; Belonenko M.B., Glazov S.Yu., Meshcheryakova N.E. // Semiconductors. 2010. V. 44. No. 9. С. 1211.

  6. Белоненко М.Б., Глазов С.Ю., Мещерякова Н.Е. // Опт. и спектроск. 2010. Т. 108. № 5. С. 818; Belonenko M.B., Glazov S.Yu., Meshcheryakova N.E. // Opt. Spectrosс. 2010. V. 108. No. 5. P. 774.

  7. Глазов С.Ю., Бадикова П.В. // Журн. нано-электрон. физ. 2018. № 2. Т. 10. С. 02020.

  8. Бадикова П.В., Глазов С.Ю. // Изв. РАН. Сер. физ. 2018. Т. 82. № 11. С. 1536; Badikova P.V., Glazov S.Yu. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. No. 11. P. 1399.

  9. Бадикова П.В., Глазов С.Ю., Сыродоев Г.А. // ФТП. 2019. Т. 53. № 7. С. 927; Badikova P.V., Glazov S.Yu., Syrodoev G.A. // Semiconductors. 2019. V. 53. No. 7. P. 911.

  10. Бадикова П.В., Глазов С.Ю., Сыродоев Г.А. // Изв. РАН. Сер. физ. 2020. Т. 84. № 1. С. 38; Badikova P.V., Glazov S.Yu., Syrodoev G.A. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No. 1. P. 29.

  11. Zhukova E.A., Urvanov S.A., Karaeva A.R. et al. // Mater. Today. Proc. 2018. V. 5. No. 12. Art. No. 25948.

  12. Бадикова П.В., Глазов С.Ю. // Учен. зап. физ. фак. МГУ. 2015. № 4. С. 154314.

  13. Глазов С.Ю. // Изв. РАН. Сер. физ. 2019. Т. 83. № 1. С. 19; Glazov S.Yu. // Bull. Russ. Acad. Sci. Phys. 2019. V. 83. No. 1. P. 12.

  14. Базь А.И., Зельдович Я.Б., Переломов А.М. Рассеяние, реакции и распады в нерелятивистской квантовой механике. М.: Наука, 1989.

  15. Попов В.С., Карнаков Б.М., Мур В.Д. // ЖЭТФ. 1998. № 113. V. 5. С. 1579; Popov V.S., Karnakov B.M., Mur V.D. // J. Exp. Theor. Phys. 1998. V. 86. No. 5. P. 860.

  16. Басс Ф.Г., Булгаков А.А., Тетервов А.П. Высокочастотные свойства полупроводников со сверхрешетками. М.: Наука, 1989.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал