Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 29-34

Об аналитических подходах, описывающих динамику пучка, распространяющегося в режиме многофотонной ионизации

В. А. Халяпин^1, 2, *, А. Н. Бугай³

¹ Федеральное государственное автономное образовательное учреждение высшего образования “Балтийский федеральный университет имени Иммануила Канта”
Калининград, Россия

² Федеральное государственное бюджетное образовательное учреждение высшего образования “Калининградский государственный технический университет”
Калининград, Россия

³ Международная межправительственная организация “Объединенный институт ядерных исследований”
Дубна, Россия

^* E-mail: slavasxi@gmail.com

Поступила в редакцию 24.08.2021
После доработки 06.09.2021
Принята к публикации 22.09.2021

EDN: OOFJGL
DOI: 10.31857/S0367676522010148

Полный текст (PDF)

Аннотация

На основе метода моментов и подхода, связанного с приосевым приближением, рассмотрена задача о распространении пучка в режиме многофотонной ионизации. Получена система уравнений на параметры пучка и найдены условия квазиустойчивого распространения. Результаты аналитических подходов верифицированы с помощью численного эксперимента.

ВВЕДЕНИЕ

Хорошо известно, что в средах с кубической нелинейностью пучки, планарные сигналы и трехмерные импульсы неустойчивы [1]. В то же время интенсивные сигналы способны генерировать плазму за счет фотоионизации и формировать плазменный канал, вдоль которого распространение может быть квазиустойчивым [2–11]. В настоящей работе рассматривается динамика оптических пучков, распространяющихся в режиме многофотонной ионизации, и рассматривается вопрос об их устойчивости с помощью двух аналитических методов: метода моментов [1, 12–14] и метода приосевого приближения [11, 15]. Представляется интересным сравнить результаты этих методов с численным экспериментом и выявить наиболее адекватный.

МЕТОД МОМЕНТОВ

В настоящей работе рассматривается динамика филаментов, распространяющихся в режиме многофотонной ионизации, с помощью метода моментов и подхода, связанного с приосевым приближением. Уравнения, описывающие соответствующую динамику, имеют вид [11]

(1)

$\begin{gathered} \frac{{\partial \psi }}{{\partial z}} - i\gamma \psi {{\left| \psi \right|}^{2}} - \frac{{i\mu }}{2}{{\Delta }_{ \bot }}\psi + \eta \left( {1 + i\frac{\omega }{\nu }} \right){{N}_{e}}\psi + \\ + \,\,\Phi \frac{{{{\sigma }^{{\left( n \right)}}}{{I}^{n}}}}{{{{{\left| \psi \right|}}^{2}}}}\psi = 0, \\ \end{gathered} $

(2)

$\frac{{\partial {{N}_{e}}}}{{\partial t}} = {{\sigma }^{{\left( n \right)}}}\left( {{{N}_{0}} - {{N}_{e}}} \right){{I}^{n}} - \beta N_{e}^{2}.$

Здесь $\psi $ – огибающая электрического поля, $z$ – координата распространения, $\eta = {{2\pi {{e}^{2}}\nu } \mathord{\left/ {\vphantom {{2\pi {{e}^{2}}\nu } {\omega {{m}_{e}}{{k}_{0}}{{c}^{2}}}}} \right. \kern-0em} {\omega {{m}_{e}}{{k}_{0}}{{c}^{2}}}}$ – параметр, связанный с электронной плазмой, e, ${{m}_{e}}$ – заряд и масса электрона соответственно, $c$ – скорость света в вакууме, ${1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0em} \mu } = {{k}_{0}}$ = ${{2\pi {{n}_{0}}} \mathord{\left/ {\vphantom {{2\pi {{n}_{0}}} {{{\lambda }_{0}}}}} \right. \kern-0em} {{{\lambda }_{0}}}}$ = = ${{\omega {{n}_{0}}} \mathord{\left/ {\vphantom {{\omega {{n}_{0}}} c}} \right. \kern-0em} c},$ ${{n}_{0}}$ – линейный показатель преломления, $\omega - $ несущая частота, $\nu $ – частота столкновения электронов с атомами, ${{\lambda }_{0}}$ – длина волны света в вакууме, ${{N}_{0}}$ – плотность нейтральных молекул, ${{N}_{e}}$ – плотность электронов, $\gamma = {{3\pi {{\chi }^{{\left( 3 \right)}}}\omega } \mathord{\left/ {\vphantom {{3\pi {{\chi }^{{\left( 3 \right)}}}\omega } {2{{n}_{0}}c}}} \right. \kern-0em} {2{{n}_{0}}c}}$ – параметр, определяющий кубическую нелинейность, ${{\chi }^{{\left( 3 \right)}}}$ – нелинейная восприимчивость третьего порядка, I – интенсивность, ${{\sigma }^{{\left( n \right)}}}$ – коэффициент $n$ – фотонной ионизации, $\beta $ – коэффициент рекомбинации электронов с положительными ионами. В соответствии с [11] можно найти равновесную электронную плотность ${{N}_{{eq}}}$ как решение уравнения (2) с нулевой производной

(3)

${{N}_{{eq}}} = \sqrt {\frac{{{{N}_{0}}\tilde {\sigma }{{{\left| \psi \right|}}^{{2n}}}}}{\beta }} ,$

где $\tilde {\sigma } = {{\sigma }^{{\left( n \right)}}}{{\left( {{{c{{n}_{0}}} \mathord{\left/ {\vphantom {{c{{n}_{0}}} {8\pi }}} \right. \kern-0em} {8\pi }}} \right)}^{n}}.$

В аналитических расчетах мы будем пренебрегать вкладом поглощения. Численный эксперимент, приведенный ниже, поможет нам определить, на каких расстояниях такой подход будет справедлив. Сперва получим уравнения на параметры филамента, используя метод моментов [12]. Выберем пробную функцию в виде

(4)

$\psi = B\exp \left[ { - \frac{1}{2}{{{\left( {\frac{r}{R}} \right)}}^{2}} + i\left( {\phi - \frac{{\varepsilon {{r}^{2}}}}{{2{{R}^{2}}}}} \right)} \right],$

где $B$ – амплитуда сигнала, $R$ – параметр, пропорциональный радиусу сигнала,$\varepsilon $ – описывает кривизну волновых поверхностей, $\varphi $ – фаза. Все параметры зависят от координаты $z.$ Определим моменты пучка следующим образом

(5)

$E = \int\limits_0^\infty {{{{\left| \psi \right|}}^{2}}2\pi rdr} ,$

(6)

${{R}^{2}} = \frac{1}{E}\int\limits_0^\infty {{{{\left| \psi \right|}}^{2}}2\pi {{r}^{3}}dr} ,$

(7)

$\varepsilon = \frac{i}{{2E}}\int\limits_0^\infty {\left( {\psi {\text{*}}{{\nabla }_{ \bot }}\psi - \psi {{\nabla }_{ \bot }}\psi {\text{*}}} \right)2\pi {{r}^{2}}dr} .$

Здесь $E$ – величина, пропорциональная мощность пучка $P = {{c{{n}_{0}}E} \mathord{\left/ {\vphantom {{c{{n}_{0}}E} {8\pi }}} \right. \kern-0em} {8\pi }}.$

Дифференцируя (5)–(7) по $z$ и используя (4), получаем систему уравнений

(8)

$\frac{{dE}}{{dz}} = 0,$

(9)

$\frac{{d{{R}^{2}}}}{{dz}} = \frac{{i\mu }}{E}\int\limits_0^\infty {\left( {\psi {{\nabla }_{ \bot }}\psi {\text{*}} - \psi {\text{*}}{{\nabla }_{ \bot }}\psi } \right)2\pi {{r}^{2}}dr} ,$

(10)

$\frac{{d\varepsilon }}{{dz}} = \frac{1}{E}\int\limits_0^\infty {\left( { - \gamma r{{{\left| \psi \right|}}^{2}}{{\nabla }_{ \bot }}{{{\left| \psi \right|}}^{2}} - \mu {{{\left| {{{\nabla }_{ \bot }}\psi } \right|}}^{2}} + \frac{{\eta \omega }}{\nu }r{{{\left| \psi \right|}}^{2}}{{\nabla }_{ \bot }}{{N}_{{eq}}}} \right)} 2\pi rdr.$

Выражение для фаз $\phi $ можно получить из уравнения

(11)

$\int\limits_0^\infty {\left( {\psi {\text{*}}\frac{{\partial \psi }}{{\partial z}} - \psi \frac{{\partial \psi {\text{*}}}}{{\partial z}} - 2i\gamma {{{\left| \psi \right|}}^{4}} + 2i\eta {{N}_{{eq}}}{{{\left| \psi \right|}}^{2}} - \frac{{i\mu }}{2}\left( {\psi {\text{*}}{{\Delta }_{ \bot }}\psi + \psi {{\Delta }_{ \bot }}\psi {\text{*}}} \right)} \right)} 2\pi rdr = 0.$

Следуя методу моментов, получаем систему уравнений

(12)

$E = \pi {{B}^{2}}{{R}^{2}} = const,$

(13)

$\frac{{d\rho }}{{dz}} = - \frac{\varepsilon }{{{{L}_{D}}\rho }},$

(14)

$\frac{{d\varepsilon }}{{dz}} = - \frac{1}{{{{L}_{D}}{{\rho }^{2}}}}\left( {1 + {{\varepsilon }^{2}}} \right) + \frac{1}{{{{L}_{N}}{{\rho }^{2}}}} - \frac{1}{{{{L}_{{{\eta }}}}{{\rho }^{n}}}},$

(15)

$\frac{{d\varphi }}{{dz}} = - \frac{1}{{{{L}_{D}}{{\rho }^{2}}}} + \frac{3}{{2{{L}_{N}}}} - \frac{{\left( {n + 1} \right)}}{{n{{L}_{\eta }}}}$.

Здесь $\rho = {R \mathord{\left/ {\vphantom {R {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$ – относительный радиус, ${{R}_{0}}$ – начальный радиус, ${{L}_{D}} = {{R_{0}^{2}} \mathord{\left/ {\vphantom {{R_{0}^{2}} \mu }} \right. \kern-0em} \mu },$ ${{L}_{N}} = {2 \mathord{\left/ {\vphantom {2 {\gamma {{B}^{2}}}}} \right. \kern-0em} {\gamma {{B}^{2}}}},$ L_η = (n + + 2)²${{\sqrt \beta } \mathord{\left/ {\vphantom {{\sqrt \beta } {4n\eta {{B}^{n}}\sqrt {\tilde {\sigma }{{N}_{0}}} }}} \right. \kern-0em} {4n\eta {{B}^{n}}\sqrt {\tilde {\sigma }{{N}_{0}}} }}$ – характерные дифракционная, нелинейная и ионизационная длины. Величина $E$ пропорциональна мощности пучка $P = {{c{{n}_{0}}E} \mathord{\left/ {\vphantom {{c{{n}_{0}}E} {8\pi }}} \right. \kern-0em} {8\pi }}.$ Решая (12)–(14), получаем уравнение, аналогичное второму закону Ньютона для частицы единичный массы в потенциальном поле

(16)

$\frac{{{{d}^{2}}\rho }}{{d{{z}^{2}}}} = - \frac{{\partial U}}{{\partial \rho }}.$

Здесь $U$ – имеет смысл энергии частицы в потенциальной яме. С точностью до константы интегрирования находим

(17)

$U = - \left( {\frac{{{{L}_{D}}}}{{{{L}_{N}}}} - 1} \right)\frac{1}{{2L_{D}^{2}{{\rho }^{2}}}} + \frac{1}{{n{{L}_{D}}{{L}_{{{\eta }}}}{{\rho }^{n}}}}.$

Устойчивое стационарное распространение пучка возможно, если выполняются условия

(18)

$\frac{{\partial U}}{{\partial \rho }}\left( {\rho = 1} \right) = 0,$

(19)

$\frac{{{{\partial }^{2}}U}}{{\partial {{\rho }^{2}}}}\left( {\rho = 1} \right) > 0.$

Отсюда с учетом (17) находим

(20)

$\frac{{{{L}_{D}}}}{{{{L}_{{{\eta }}}}}} = \frac{{{{L}_{D}}}}{{{{L}_{N}}}} - 1,$

(21)

$n > 2.$

Условие (20) можно переписать в виде

(22)

$\frac{1}{{{{R}_{0}}}} = \sqrt {\frac{{\pi I}}{{{{P}_{c}}}} - \frac{{4n\eta {{k}_{0}}{{I}^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0em} 2}}}}}}{{{{{\left( {n + 2} \right)}}^{2}}}}\sqrt {\frac{{{{\sigma }^{{\left( n \right)}}}{{N}_{0}}}}{\beta }} } ,$

где ${{P}_{c}}$ – критическая мощность, определяемая выражением

(23)

${{P}_{c}} = \frac{{c{{n}_{0}}}}{{4{{k}_{0}}\gamma }} = \frac{{с\lambda _{0}^{2}{{n}_{0}}}}{{24{{\pi }^{3}}{{\chi }^{{\left( 3 \right)}}}}}.$

Таким образом, стационарное решение для плоского фронта и начального радиуса, определяемого согласно (22), имеет вид

(24)

$\begin{gathered} \psi = \frac{{8\pi I}}{{c{{n}_{0}}}} \times \\ \times \,\,\exp \left[ { - \frac{1}{2}{{{\left( {{{{\frac{r}{R}}}_{0}}} \right)}}^{2}} + i\left( { - \frac{1}{{{{L}_{D}}}} + \frac{3}{{2{{L}_{N}}}} - \frac{{\left( {n + 1} \right)}}{{n{{L}_{{{\eta }}}}}}} \right)z} \right]. \\ \end{gathered} $

МЕТОД ПРИОСЕВОГО ПРИБЛИЖЕНИЯ

Применим другой аналитический подход к решению данной задачи. Для этого пробное решение (4) подставляем в (1) и рассматриваем приосевую область пучка (${{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}} \ll 1$). Это позволяет в нелинейных слагаемых использовать разложение ${{\left| \psi \right|}^{n}} \approx {{B}^{n}}\left( {{{1 - n{{r}^{2}}} \mathord{\left/ {\vphantom {{1 - n{{r}^{2}}} {2{{R}^{2}}}}} \right. \kern-0em} {2{{R}^{2}}}}} \right).$ Приравнивая слагаемые перед нулевой и второй степенями $r$ и отделяя действительную и мнимую части, находим систему уравнений

$\frac{{dB}}{{dz}} = \frac{{B\varepsilon }}{{{{L}_{D}}{{\rho }^{2}}}},$

(26)

$\frac{{d\rho }}{{dz}} = - \frac{\varepsilon }{{{{L}_{D}}\rho }},$

(27)

$\frac{{d\varepsilon }}{{dz}} = - \frac{1}{{{{L}_{D}}{{\rho }^{2}}}}\left( {1 + {{\varepsilon }^{2}}} \right) + \frac{4}{{{{L}_{N}}{{\rho }^{2}}}} - \frac{1}{{{{L}_{{{\eta }}}}{{\rho }^{n}}}}{{\left( {\frac{n}{2} + 1} \right)}^{2}},$

(28)

$\frac{{d\varphi }}{{dz}} = - \frac{1}{{{{L}_{D}}{{\rho }^{2}}}} + \frac{2}{{{{L}_{N}}}} - \frac{1}{{n{{L}_{{{\eta }}}}}}{{\left( {\frac{n}{2} + 1} \right)}^{2}}.$

Легко показать, что из (25) и (26) можно перейти к выражению (12). Сравнивая систему (12)–(15) и (25)–(26), можно заметить, что линейные слагаемые у них одинаковы, а различия проявляются в нелинейных слагаемых (кубическая нелинейность и ионизация). Для этого подхода начальный радиус пучка, при котором реализуется квазиустойчивый баланс между нелинейностью, дифракцией и ионизационной расходимостью, определяется следующим образом

(29)

$\frac{1}{{{{R}_{0}}}} = \sqrt {\frac{{4\pi I}}{{{{P}_{c}}}} - n\eta {{k}_{0}}{{I}^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0em} 2}}}}\sqrt {\frac{{{{\sigma }^{{\left( n \right)}}}{{N}_{0}}}}{\beta }} } .$

Из сравнения (22) и (29) видно, что без учета вклада ионизации критическая мощность, определяемая с помощью метода моментов, в четыре раза больше таковой, получаемой с помощью приосевого приближения. Слагаемые же, связанные с ионизацией, по-разному себя ведут в зависимости от $n.$ Стационарное решение в этом подходе определяется согласно

(30)

$\begin{gathered} \psi = \frac{{8\pi I}}{{c{{n}_{0}}}}\exp \,\left[ { - \frac{1}{2}{{{\left( {{{{\frac{r}{R}}}_{0}}} \right)}}^{2}} + } \right. \\ \left. { + \,\,i\left( { - \frac{1}{{{{L}_{D}}{{\rho }^{2}}}} + \frac{2}{{{{L}_{N}}}} - \frac{1}{{n{{L}_{{{\eta }}}}}}{{{\left( {\frac{n}{2} + 1} \right)}}^{2}}} \right)z} \right]. \\ \end{gathered} $

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Представляет интерес численное исследование, которое позволит выявить, какой из подходов дает лучшие результаты в рамках данной задачи. В качестве среды рассмотрим воздух, где основной вклад в образование плазмы дает кислород. Материальные параметры, входящие в уравнения (1), (2) для импульсов на длине волны 248.6 нм, взяты из [11].

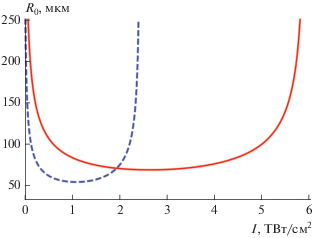
Как видно из рис. 1 метод моментов и приосевое приближение дают различные предсказания для стационарного радиуса филамента в зависимости от его интенсивности. Отметим, что существует верхний предел по интенсивности филамента. Рассматриваемые подходы дают для данного предела различие примерно в 2.5 раза.

Рис. 1

Зависимость стационарного радиуса филамента ${{R}_{0}}$ от его пиковой интенсивности I в воздухе на длине волны 248.6 нм. Сплошная кривая соответствует формуле (22) (предсказание метода моментов), а штриховая кривая – формуле (29) (предсказание приосевого приближения).

Проведем теперь численное интегрирование исходной системы уравнений в частных производных (1), (2), задав в качестве начальных условий выражения (24) и (30), предсказывающие стационарный режим распространения филамента методом моментов и приосевым приближением, соответственно. Краевые условия соответствуют нулевым значениям поля и концентрации электронов на границе области.

Результаты расчетов для начальной пиковой интенсивности ${\rm I} = 1.8 \cdot {{10}^{{12}}}\,\,{\text{Вт}} \cdot {\text{с}}{{{\text{м}}}^{{ - {\text{2}}}}}$ приведены на рис. 2 и 3 . В этом случае метод моментов и приосевое приближение дают близкие предсказания для стационарного радиуса филамента, ${{R}_{0}} = 70$ нм и ${{R}_{0}} = 63$ нм, соответственно. Как показывает моделирование, метод моментов дает лучший результат в рамках данной задачи. Амплитуда и радиус филамента отличаются от теоретического предсказания не более чем на 5% (рис. 2а, рис. 3а), в то время как в противоположном случае развивается осцилляционной режим относительно среднего значения амплитуды на 20% меньше ожидаемого (рис. 2а, рис. 3б). Для начальной пиковой интенсивности $I = 3 \cdot {{10}^{{12}}}\,\,{\text{Вт}} \cdot {\text{с}}{{{\text{м}}}^{{ - {\text{2}}}}}$ приосевое приближение предсказывает отсутствие устойчивого режима. В этом случае численное моделирование (1), (2) с начальным условием (24), где ${{R}_{0}} = 68$ нм, показывает хорошее соответствие с предсказанием метода моментов аналогично пунктирной кривой на рис. 2а. При интенсивностях ${\rm I} = 1.6 \cdot {{10}^{{12}}}\,\,{\text{Вт}} \cdot {\text{с}}{{{\text{м}}}^{{ - {\text{2}}}}}$ и меньше предсказание приосевого приближения для квазистационарного режима не оправдывается, а развивается дефокусировка филамента.

Рис. 2.

Изменение пиковой амплитуды филамента при его распространении в среде, соответствующая численному решению (1), (2) с начальным условием (24) при R₀ = 70 нм (пунктирная кривая), и с начальным условием (30) при R₀ = = 63 нм (сплошная кривая) и начальной интенсивности I = 1.8 · 10¹² Вт · см^–2 без учета (а) и с учетом (б) эффектов поглощения. Штриховая линия соответствует ожидаемому в теории стационарному режиму.

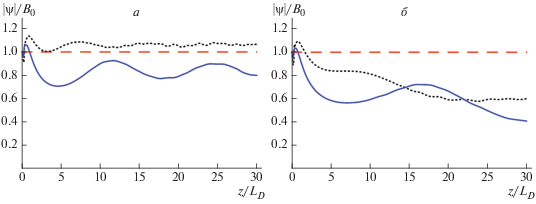
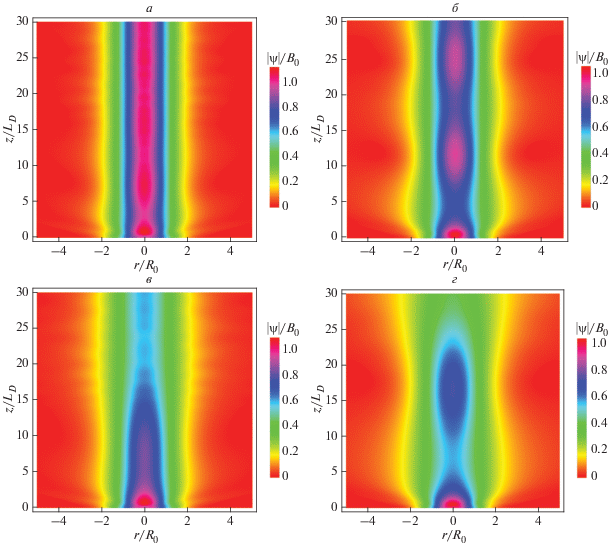
Рис. 3.

Пространственная динамика филамента при его распространении в среде, соответствующая численному решению (1), (2) с начальным условием (24) при R₀ = 70 нм (а, в), и с начальным условием (30) при R₀ = 63 нм (б, г) и начальной интенсивности I = 1.8 · 10¹² Вт · см^–2 без учета (а, б) и с учетом (в, г) эффектов поглощения. Цветом обозначено относительное изменение амплитуды.

Следует отметить, что рассматриваемый баланс носит квазиустойчивый характер вследствие влияния нелинейного поглощения. Характерный масштаб проявления эффектов поглощения за счет потерь энергии на ионизацию среды можно оценить как ${{L}_{{abs}}} = {B \mathord{\left/ {\vphantom {B {(\Phi {{\sigma }^{{\left( n \right)}}}{{I}^{n}})}}} \right. \kern-0em} {(\Phi {{\sigma }^{{\left( n \right)}}}{{I}^{n}})}}.$ Как следует из рис. 2б, квазиустойчивый филамент постепенно теряет энергию, а его радиус при этом изменяется незначительно (рис. 3в, 3г). Таким образом, поглощение не приводит к распаду филамента, а лишь к ослаблению его интенсивности.

ЗАКЛЮЧЕНИЕ

Получено аналитическое описание распространения филаментов в режиме взаимной компенсации эффектов дифракции и ионизационной расходимости, с одной стороны, и самофокусировки, с другой. С помощью метода моментов и метода приосевого приближения проанализирована динамика филаментов в газе в режиме многофотонной ионизации (для произвольного порядка процесса ионизации). Получены условия квазистационарного распространения филамента. Следует отметить, что более простое математически приосевое приближение следует использовать с осторожностью в данной задаче, так как происходит недооценка роли профиля импульса. Численное моделирование показывает, что потери на ионизацию не приводят к распаду филамента, а лишь к ослаблению его интенсивности, вследствие чего рассмотренный режим можно считать квазиустойчивым.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 19-02-00234а).

Список литературы

Kivshar Yu.S., Agrawal G.P. Optical solitons: from fibers to photonic crystals. N.Y.: Academic Press Inc., 2003.
Couairon A. // Eur. Phys. J. D. 1996. V. 27. P. 159.
Henz S., Herrmann J. // Phys. Rev. E. 2006. V. 53. Art. No. 4092.
Sprangle P., Penano J.R., Hafizi B. // Phys. Rev. E. 2002. V. 66. Art. No. 046418.
Esarey E., Sprangle P., Ting A. // Quant. Electron. 1997. V. 33. P. 1879.
Sprangle P., Esarey E., Krall J. // Phys. Rev. E. 1996. V. 54. Art. No. 4211.
Penano J., Palastro J.P., Hafizi B. et al. // Phys. Rev. A. 2017. V. 96. Art. No. 013829.
Couairon A., Mysyrowicz A. // Phys. Rep. 2007. V. 441. P. 47.
Chekalin S.V., Dokukina E.A., Dormidonov A.E. et al. // J. Phys. B. 2015. V. 48. Art. No. 094008.
Воронин А.А., Желтиков А.М. // УФН. 2016. Т. 186. № 9. С. 957; Voronin A.A., Zheltikov A.M. // Phys. Usp. 2016. V. 59. P. 869.
Schwarz J., Diels J.C. // Phys. Rev. A. 2001. V. 65. Art. No. 013806.
Santhanam J., Agraval G. // Opt. Commun. 2003. V. 222. P. 413.
Власов С.Н., Петрищев В.А., Таланов В.И. // Изв. вузов. Радиофиз. 1971. Т. 14. № 9. С. 1453.
Маймистов А.И. // ЖЭТФ. 1993. Т. 104. № 5. С. 3620.
Ахманов С.А., Сухоруков А.П., Хохлов Р.В. // УФН. 1967. Т. 93. С. 19; Akhmanov S.A., Sukhorukov A.P., Khokhlov R.V. // Sov. Phys. Usp. 1968. V. 10. P. 609.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал