Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 35-41

ВВЕДЕНИЕ

Многослойные неоднородные голографические дифракционные структуры (МНГДС), разделенные промежуточными слоями, вызывают большой интерес у исследователей в связи с их возможным применением в оптических устройствах связи, например, в оптических мультиплексорах [1–6].

Так, в работах [1, 6–10] многослойные дифракционные структуры исследованы на основе фотополимерного материала (ФПМ). В работе [1] было показано, что вследствие неоднородностей профилей решеток по глубине существенно может изменяться вид селективности дифрагировавшего пучка. А ряд локальных максимумов, количество и ширина определяются толщиной промежуточных слоев. В своей работе неоднородность профиля решеток авторы обуславливали модуляцией показателя преломления, описываемого ослаблением света по закону Бугера–Ламберта–Бера. Однако, в исследованиях [9–12] неоднородность профилей решеток по глубине объясняли влиянием фотоиндуцированного поглощения света в материале, при котором профиль решеток мог трансформироваться в процессе записи. Также в работах [9, 10] было показано, что, варьируя составом для каждого слоя, возможно создать однородные профили близкие к друг другу, что может улучшить дифракционные характеристики элемента.

Однако в данных работах не было рассматрено возможности динамического управления видом селективного отклика таких структур. Реализация динамического управления возможна при наличии жидких кристаллов (ЖК) в составе ФПМ [13, 14]. Директор ЖК чувствителен к электромагнитным воздействиям, тем самым может изменять свою пространственную ориентацию, и как следствие, меняются условия распространения электромагнитных волн.

Таким образом, исследование дифракции света на многослойных неоднородных голографических ФПМ-ЖК структурах становится актуальным.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

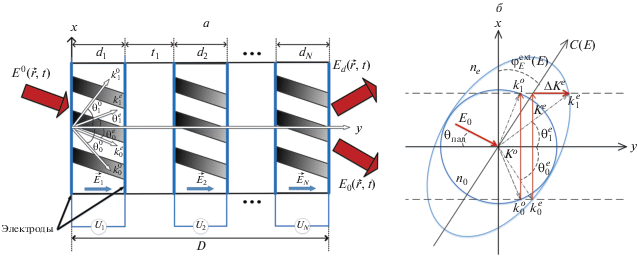
В данной работе рассматривается дифракция света на пропускающей голографической многослойной дифракционной структуре в ФПМ-ЖК (рис. 1). Будем считать, что ЖК капсулированы полимером (КПЖК), для которых характерно объединение молекул ЖК в капсулы. Дифракция происходит на структурах, на которых закончились все процессы записи. Апертура считывающего пучка много больше толщины слоя ФПМ-ЖК. Таким образом, процессы дифракции будут описываться в геометрооптическом приближении. Рассмотрена дифракции только на основной пространственной гармонике показателя преломления дифракционной структуры.

ФПМ-ЖК является анизотропной средой, следовательно, пучок света внутри образца распадается на две волны: обыкновенную и необыкновенную (рис. 1а, 1б).

Амплитудные профили пучков $E_{j}^{m}$ для каждого слоя находятся из решения системы уравнений связанных волн в частных производных [13, 14]:

где $E_{j}^{{n,m}}(\vec {r})$ – амплитудные профили пучков, $\vec {N}_{{rj}}^{{n,m}}$ – групповые нормали, $C_{j}^{{n,m}}(\vec {r},E)$ – амплитудные коэффициенты связи, $n_{n}^{{n,m}}(\vec {r})$ – нормированный амплитудный профиль показателя преломления структуры, $\Delta {{\vec {K}}^{{n,m}}}$ – вектор фазовой расстройки.

Входящие в выражения (1) и (2) коэффициенты связи определяются [13]:

где $n_{0}^{{n,m}}(\vec {r},E)$ = ${{\left[ {n_{{lc}}^{0}n_{{lc}}^{e}} \right]} \mathord{\left/ {\vphantom {{\left[ {n_{{lc}}^{0}n_{{lc}}^{e}} \right]} {[n{{{_{{lc}}^{e}}}^{2}} \cdot {{{\sin }}^{2}}({{\varphi }}_{E}^{{ext}}(\vec {r},E) - {{\theta }}_{0}^{m})}}} \right. \kern-0em} {[n{{{_{{lc}}^{e}}}^{2}} \cdot {{{\sin }}^{2}}({{\varphi }}_{E}^{{ext}}(\vec {r},E) - {{\theta }}_{0}^{m})}}$ + + $n_{{lc}}^{{02}} \cdot {{\cos }^{2}}({{\varphi }}_{E}^{{ext}}(\vec {r},E) - {{\theta }}_{0}^{m}){{]}^{{ - 0.5}}},$ $n_{1}^{{n,m}}(\vec {r},E)$ = = ${{\left[ {n_{{lc}}^{0}n_{{lc}}^{e}} \right]} \mathord{\left/ {\vphantom {{\left[ {n_{{lc}}^{0}n_{{lc}}^{e}} \right]} {[n{{{_{{lc}}^{e}}}^{2}} \cdot {{{\sin }}^{2}}({{\varphi }}_{E}^{{ext}}(\vec {r},E) - {{\theta }}_{1}^{m})}}} \right. \kern-0em} {[n{{{_{{lc}}^{e}}}^{2}} \cdot {{{\sin }}^{2}}({{\varphi }}_{E}^{{ext}}(\vec {r},E) - {{\theta }}_{1}^{m})}}$ + $n_{{lc}}^{{02}} \cdot {{\cos }^{2}}$ × × $({{\varphi }}_{E}^{{ext}}(\vec {r},E) - {{\theta }}_{1}^{m}){{]}^{{ - 0.5}}}$, ${{\hat {\varepsilon }}}$ – амплитуда основной гармоники возмущения тензора диэлектрической проницаемости, $n_{{lc}}^{e}$ и $n_{{lc}}^{0}$ – необыкновенный и обыкновенный показатели преломления ЖК, ${{c}_{c}}$ – скорость света в вакууме, ${{\omega }}$ – угловая частота световых волн, ${{\varphi }}_{E}^{{ext}}(E)$ – угол поворота капсул ЖК, который может быть найден как [13]: где ${{{{\varphi }}}_{{\text{0}}}}$ – угол между вектором напряженности электрического поля и директором капсулы при $E = 0,$ ${{e}^{2}}(\vec {r})$ = $E\left( {\vec {r}} \right)R\sqrt {{{{{\Delta \bar {\varepsilon }}}} \mathord{\left/ {\vphantom {{{{\Delta \bar {\varepsilon }}}} {{{K}_{{33}}}\left( {5.7{{\delta }}_{{LC}}^{2} + 2.1{{{{\lambda }}}_{k}}} \right)}}} \right. \kern-0em} {{{K}_{{33}}}\left( {5.7{{\delta }}_{{LC}}^{2} + 2.1{{{{\lambda }}}_{k}}} \right)}}} $ – параметр, характеризующий действие электрического поля на биполярную капсулу ЖК, $R$ – радиус капли, ${{{{\delta }}}_{{LC}}}$ – эксцентриситет капсулы, ${{{{\lambda }}}_{k}} = {{R{{W}_{{{\alpha }}}}} \mathord{\left/ {\vphantom {{R{{W}_{{{\alpha }}}}} {{{K}_{{33}}}}}} \right. \kern-0em} {{{K}_{{33}}}}}$ – параметр поверхностного сцепления, ${{W}_{{{\alpha }}}}$ – коэффициент азимутального поверхностного сцепления, ${{\Delta \bar {\varepsilon }}}$ – диэлектрическая анизотропия биполярной капсулы.

Критическая напряженность электрического поля фотоиндуцированного перехода Фредерикса, при котором происходит вращение директора ЖК, определяется как [13]:

где ${{\varepsilon }}_{{lc}}^{e} = {{\left( {n_{{lc}}^{e}} \right)}^{2}}$ и ${{\varepsilon }}_{{lc}}^{0} = {{\left( {n_{{lc}}^{0}} \right)}^{2}}$ – компоненты тензора, измеренные при продольной и поперечной ориентации директора ЖК. При этом тензор диэлектрической проницаемости каждого слоя зависит от ориентации директора ЖК в нем: где ${{\rho }}$ – доля ЖК в составе, ${{{{\varepsilon }}}_{p}} = n_{p}^{2}$ – диэлектрическая проницаемость полимера, ${{\hat {I}}}$ – единичный тензор. А изменение тензора (7) определяется в виде суммы пространственных гармоник диэлектрической проницаемости: где $p({{\alpha }})$ и $q(\phi )$ – гауссовы функции распределения молекул ЖК в капсуле эллипсоидального вида [13], $\vec {С}{\text{(}}\vec {r}{\text{,}}E{\text{)}}$ – ориентация директора КПЖК, который выражается через угол поворота, описанного в выражении (5):

Взаимодействие световых полей 0-го и 1-го дифракционных порядков в n-м слое МНГДС решается матричным методом в виде [9, 10]:

где ${{\vec {E}}^{{n,m}}} = \left[ {\begin{array}{*{20}{c}} {E_{0}^{{n,m}}\left( {E,\Delta K} \right)} \\ {E_{1}^{{n,m}}\left( {E,\Delta K} \right)} \end{array}} \right];$ ${{\vec {T}}^{{n,m}}}$ = = $\left[ {\begin{array}{*{20}{c}} {T_{{00}}^{{n,m}}\left( {E,\Delta K} \right)}&{T_{{10}}^{{n,m}}\left( {E,\Delta K} \right)} \\ {T_{{01}}^{{n,m}}\left( {E,\Delta K} \right)}&{T_{{11}}^{{n,m}}\left( {E,\Delta K} \right)} \end{array}} \right];$ ${{\vec {E}}^{{'n - 1,m}}}$ = = $\left[ {\begin{array}{*{20}{c}} {E_{0}^{{'n - 1,m}}\left( {E,\Delta K} \right)} \\ {E_{1}^{{'n - 1,m}}\left( {E,\Delta K} \right)} \end{array}} \right];$ ${{\vec {T}}^{{n,m}}}$ – матричная передаточная функция n-го слоя МНГДС; $E_{j}^{{'n - 1,m}}\left( {E,\Delta K} \right)$ и $E_{j}^{{n,m}}\left( {E,\Delta K} \right)$ – частотно-угловые спектры (ЧУС) на входе и выходе n-го слоя, $E$ – прикладываемое напряжение. Элементы передаточной матрицы ${{\vec {T}}^{{n,m}}}$ выражаются как [9, 10]: где ${}_{2}{{F}_{1}}$ – гипергеометрическая функция Гаусса; $w(q)$ = $\frac{{\operatorname{sh} \left( {{{cs(1 - q)} \mathord{\left/ {\vphantom {{cs(1 - q)} 2}} \right. \kern-0em} 2}} \right)\operatorname{sh} \left( {{{cs(1 + q)} \mathord{\left/ {\vphantom {{cs(1 + q)} 2}} \right. \kern-0em} 2}} \right)}}{{\operatorname{ch} \left( {cs} \right)\operatorname{ch} \left( {c(s - t)} \right)}};$ $b_{p}^{{n,m}}(E) = $ $ = {{\left[ {{{d}_{n}} \cdot C_{j}^{{n,m}}(E)} \right]} \mathord{\left/ {\vphantom {{\left[ {{{d}_{n}} \cdot C_{j}^{{n,m}}(E)} \right]} {\sqrt {{{\nu }_{0}} \cdot {{\nu }_{1}}} }}} \right. \kern-0em} {\sqrt {{{\nu }_{0}} \cdot {{\nu }_{1}}} }}$; A = [cs ch (ct)${{\left. {\operatorname{ch} \left( {c\left( {s - t} \right)} \right)} \right]}^{{ - 1}}};$ ${{d}_{n}}$ – толщина n-го слоя; ${{{{\nu }}}_{0}} = \cos \left( {{{\theta }}_{{rj}}^{{n,m}}} \right);$ ${{\theta }}_{{rj}}^{{n,m}}$ – углы между групповыми нормалями $\vec {N}_{{rj}}^{{n,m}}$ и осью y.

Параметры c, s, t находятся для каждого слоя отдельно путем аппроксимации нормированного пространственного профиля амплитуды первой гармоники показателя преломления ${{n}_{1}}(y)$ ГДС, полученной при записи МНГДС, функцией ${{n}_{1}}(y,c,s,t)$= ${\text{c}}{{{\text{h}}}^{{ - 1}}}\left[ {c(sy - t)} \right].$ Параметры c, s, t определяют степень неоднородности, асимметрии и смещения ${{n}_{1}}(y).$

Таким образом, передаточные функции создают математическую основу для расчета селективных свойств МНГДС, зависящих от прикладываемого напряжения, угла падения и центральной частоты считывающего излучения. При этом модуль вектора фазовой расстройки также зависит от напряжения:

где $\Delta {{K}^{{n,m}}}({{\theta }}) = ({D \mathord{\left/ {\vphantom {D B}} \right. \kern-0em} B}){{\theta }}$ и $\Delta {{K}^{{n,m}}}({{\omega }})$ = $(C - {{AD} \mathord{\left/ {\vphantom {{AD} B}} \right. \kern-0em} B}){{\omega }}$ – отражают отклонение от условий фазового синхронизма, коэффициенты A, B, C, D определены в [13], $\Delta {{K}^{{n,m}}}(E)$ = ${{{\omega }} \mathord{\left/ {\vphantom {{{\omega }} {{{c}_{c}}}}} \right. \kern-0em} {{{c}_{c}}}}\left[ {n_{0}^{{n,m}}(E)\left( {\vec {N}_{0}^{{n,m}} \cdot {{{\vec {y}}}_{0}}} \right)} \right.$ – $n_{1}^{{n,m}}(E)$ × × $\left. {\left( {\vec {N}_{1}^{{n,m}} \cdot {{{\vec {y}}}_{0}}} \right)} \right]$ + $\left( {{{{\vec {K}}}^{{n,m}}} \cdot {{{\vec {y}}}_{0}}} \right).$

Промежуточный слой толщиной ${{t}_{n}}$ дает фазовый набег. Будем считать, что показатель преломления промежуточного слоя равен показателю преломления голограммы. Тогда матрица перехода ${{\vec {A}}^{{n,m}}}$ будет выглядеть как [9, 10]:

Связь между входным ${{\vec {E}}_{0}}$ и дифракционным ${{\vec {E}}^{{N,m}}}$ полем из выражения (8) на выходе МНГДС:

где ${{\vec {T}}^{m}} = {{\vec {T}}^{{N,m}}} \cdot {{\vec {A}}^{{N - 1,m}}} \cdot {{\vec {T}}^{{N - 1,m}}}$…${{\vec {A}}^{{n,m}}} \cdot {{\vec {T}}^{{n,m}}} \ldots $ … ${{\vec {A}}^{{1,m}}} \cdot {{\vec {A}}^{{1,m}}}$ – матричная передаточная функция всей МНГДС.

При численном моделировании будем рассматривать случай взаимодействия только плоских квазимонохроматических световых пучков, с единичной амплитудой. В этом случае ${{\vec {E}}_{0}} = {{\delta }}({{\omega }},{{\theta }}),$ а $\int {\int {\left( {{{{\vec {E}}}_{0}} \cdot \vec {E}_{0}^{*}} \right)d{{\omega }}} d{{\theta }}} = 1.$ Поляризация падающего излучения совпадает с поляризацией собственных необыкновенных волн в каждом слое. Таким образом, дифракционную эффективность на выходе МНГДС можем определить как [9, 10]:

где $E_{1}^{{N,m}}(E,\Delta K)$ – выражается через элементы $T_{{ij}}^{{n,m}}$ матричных передаточных функций ${{\vec {T}}^{{N,m}}}$ слоев.

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Численное моделирование дифракционных характеристик МНГДС проводилось по выражению (11). Для моделирования использовалась ГДС с неоптимизированным и оптимизированным составом. Использование оптимизированного состава, полученного путем подбора концентрации красителя для каждого слоя ФПМ-ЖК, позволял достигать практически равных и однородных профилей решеток при голографической записи МНГДС. МНГДС состояла из двух или трех слоев ФПМ-ЖК толщиной d_n = 85 мкм, разделенных промежуточным слоем t_n = 400 мкм. Также использовались следующие параметры: λ = 633 нм – длина волны излучения; $n_{{lc}}^{0}$ = 1.535 и $n_{{lc}}^{e}$ = 1.680 – обыкновенный и необыкновенный показатель преломления ЖК; ${{n}_{p}}$ = 1.535 – показатель преломления полимера; θ_b = 10 градусов – угол Брэгга; ${{K}_{{33}}} = 7.45 \cdot {{10}^{{ - 2}}};$ $c = 0.36;0.31,0.43,$ $s = 1.03;0.68,0.24,$ $t = - 0.9; - 1.04, - 0.72$ и c = 1.46; 0.89, $s = 1.41;2.69,$ $t = 0.71; - 0.6$ – параметры для профилей решеток с оптимизированным и неоптимизированным составом. Данные параметры получены путем аппроксимации нормированных пространственных профилей амплитуды первой гармоники показателя преломления ${{n}_{1}}(y)$ для каждого слоя записанной МНГДС функцией вида ${{n}_{1}}(y,c,s,t).$

По выражению (11) получены зависимости дифракционной эффективности для двухслойной и трехслойной дифракционных структур от изменения фазовой расстройки и приложенного электрического поля.

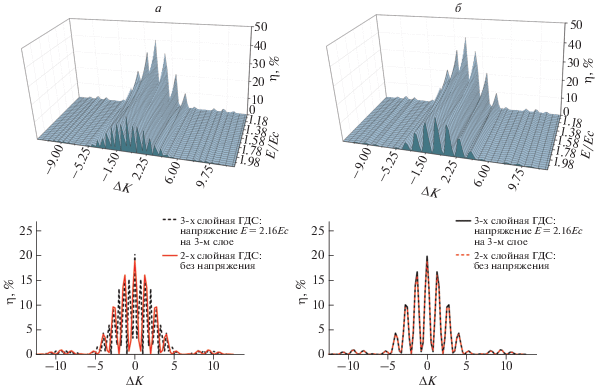
При неоптимизированном составе профили решеток МНГДС различны после завершения записи, поэтому вид селективного отклика для двухслойной ГДС искажается, локальные минимумы не достигают нуля (рис. 2а). При воздействии внешнего электрического поля к каждому слою, происходит плавное снижение дифракционной эффективности всей ГДС (рис. 2а, 2б).

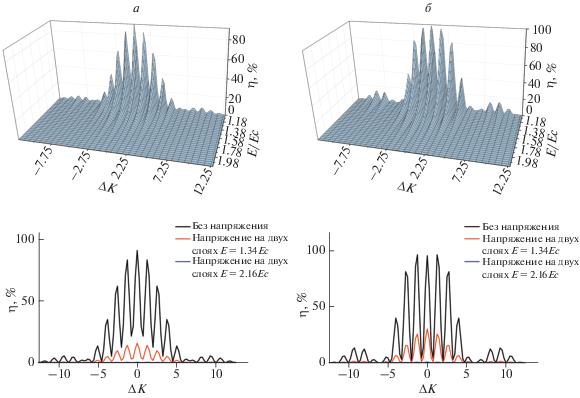
Для двухслойной ГДС с оптимизированным составом, вследствие практически равных и однородных профилей решеток после голографической записи, вид селективного отклика не искажается. При воздействии приложенного электрического поля на втором слое, происходит трансформация селективного отклика (рис. 3а). При этом дифракционная характеристика и вид селективного отклика соответствует одиночной ГДС (рис. 3б). Стоит отметить, что воздействие приложенного электрического поля только для первого слоя приводит практически к аналогичной трансформации.

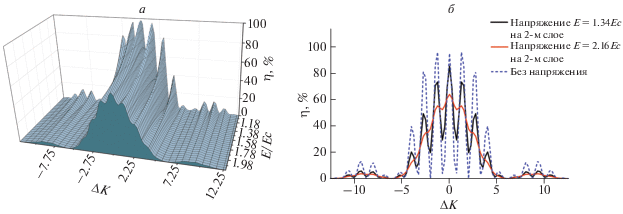
Для трехслойной ГДС, при воздействии приложенного электрического поля на втором слое, происходит трансформация селективного отклика, соответствующей двухслойной ГДС с увеличенной толщиной промежуточного слоя (рис. 4а). Следовательно, наблюдается появление дополнительных локальных максимумов контура селективности. При воздействии приложенного электрического поля на третьем слое происходит трансформация селективного отклика, соответствующей стандартной двухслойной ГДС (рис. 4б).

ЗАКЛЮЧЕНИЕ

Развита теоретическая модель дифракции квазимонохроматических световых пучков на пространственно-неоднородных многослойных дифракционных структурах, сформированных в фотополимерном материале с капсулированными нематическими жидкими кристаллами.

Показано, что при использовании приложенного электрического поля в каждому слою возможно динамически управлять видом селективного отклика многослойной дифракционной структуры. При воздействии внешнего электрического поля к каждому слою ФПМ-ЖК наблюдается плавное снижение дифракционной эффективности всей МНГДС, тогда как воздействие только на отдельный слой приводит к трансформации вида селективного отклика. Таким образом, манипулируя электрическим полем на каждом из слоев МНГДС с ФПМ-ЖК можно варьировать значением дифракционной эффективности и видом селективности.

Установлено, что оптимизация состава для каждого слоя таких структур, осуществленной путем изменения внутренних параметров, например концентрации красителя, позволяет добиться практически одинаковых и близких к однородным профилей решеток при записи МНГДС, что в итоге приводит к улучшению вида селективного отклика.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках темы государственного задания на 2020–2022 годы (номер темы FEWM-2020-0038/3).