Известия РАН. Серия физическая, 2022, T. 86, № 1, стр. 128-134

ВВЕДЕНИЕ

Пространственное распределение температуры внутри организма несет информацию, важную при диагностике заболеваний и при проведении операций, связанных с нагревом тканей. Одним из возможных способов регистрации внутренней температуры является акустотермометрия [1]. Данный метод основан на анализе собственного шумового акустического излучения нагретого тела. Причиной его возникновения является тепловое хаотическое движение частиц. Уравнение движения среды, учитывающее это движение, содержит источники поля в виде случайной силы, которую можно описать с помощью корреляционной функции ее пространственных компонент [2]. Для жидких сред ситуация несколько упрощается: акустическое поле описывается волновым уравнением с некоррелированными в пространстве и времени термоакустическими источниками, мощность которых в каждой точке пропорциональна абсолютной температуре $T$ и амплитудному коэффициенту поглощения звука $\alpha $ в среде. Например, в одномерном случае средний квадрат давления звуковой волны p, которая создается термоакустическими источниками, распространяется вдоль оси $x$ в однородной среде и регистрируется на приемнике с координатой ${{x}_{0}},$ определяется как [3, 4]

где $q$ – размерностный коэффициент; ${{f}_{0}}$ и $\Delta f$ – средняя частота и ширина спектра принимаемого сигнала, соответственно; ${{\rho }_{0}}$ и ${{c}_{0}}$ – плотность и скорость звука в среде; ${{k}_{{\text{B}}}}$ – постоянная Больцмана. При этом множитель ${{I}_{F}} = 2q\alpha (x)T(x)$ характеризует пространственное распределение линейной плотности мощности термоакустических источников излучения, а множитель $\exp \left[ { - \int_x^{{{x}_{0}}} {2\alpha (x{\kern 1pt} ')dx{\kern 1pt} '} } \right]$ определяет затухание энергии волны при распространении в среде. Если температура среды всюду одинакова, т.е. $T(x) \equiv T = {\text{const,}}$ то, согласно (1), получается $\left\langle {{{p}^{2}}} \right\rangle = {{qT} \mathord{\left/ {\vphantom {{qT} 2}} \right. \kern-0em} 2}.$ Это в два раза меньше значения $qT$ квадрата звукового давления для термоакустического излучения в однородной среде, поскольку в (1) учитываются источники, лежащие только с одной стороны от приемника.

Следует отметить, что собственное акустическое излучение организма слабое, а из-за поглощения среды оно быстро затухает на высоких частотах. При этом в практических медицинских приложениях требуется фиксировать его изменения при нагреве порядка единицы или даже десятых долей градуса [5]. В настоящее время развиваются интенсиометрический [1, 5, 6] и корреляционный [7–13] методы регистрации термоакустического излучения. Подробно вопросы корреляционного приема термоакустического излучения обсуждаются также в монографии [14]. В представляемой работе для каждого из этих двух методов определена их чувствительность при исследовании плоских слоев, а также экспериментально показана возможность отслеживать изменение температуры слоя во времени.

СХЕМА ИЗМЕРЕНИЙ И ОЦЕНКИ ЧУВСТВИТЕЛЬНОСТИ

Рассматривается одномерная задача корреляционного приема термоакустического излучения от однородного поглощающего слоя с толщиной $h$, равномерно нагретого до температуры T. Ось OX, соответствующая одномерному пространству, имеет начало отсчета в середине слоя. В плоскости, перпендикулярной оси OX, размеры слоя предполагаются неограниченными. Поверхности двух плоских приемных гидрофонов расположены перпендикулярно оси OX; центры этих гидрофонов находятся вне слоя и имеют координаты ${{l}_{1}} < - \,0.5h$ и ${{l}_{2}} > 0.5h.$ Волновое число вне слоя ${{k}_{0}}$ действительное, а внутри слоя $k + i\alpha $ – комплексное, что означает наличие поглощения в слое. Термоакустические источники $F(x)\exp ( - i\omega t)$ расположены в каждой точке $\left| x \right| < 0.5h$ слоя. Сигналы, регистрируемые гидрофонами 1 и 2 от всех точек слоя без учета отражения волн от его границы, соответственно равны

Следует отметить, что здесь и ниже используется комплексное аналитическое представление сигналов. В эксперименте регистрируются действительные сигналы. Поэтому их следует предварительно дополнить до комплексных, например, с помощью преобразования Гильберта. Функция когерентности $\Gamma (\tau )$ сигналов (2) и (3) для временной задержки, равной ${{\tau }_{{layer}}} = {{{{k}_{0}}({{l}_{2}} + {{l}_{1}})} \mathord{\left/ {\vphantom {{{{k}_{0}}({{l}_{2}} + {{l}_{1}})} \omega }} \right. \kern-0em} \omega },$ что соответствует фазированию на середину слоя, определяется как

где звездочкой обозначено комплексное сопряжение, а операция 〈⋅〉 означает усреднение по множеству реализаций случайного процесса во времени. Множитель ${{I}_{F}} = 2q\alpha T,$ как и в (1), определяет линейную плотность мощности термоакустических источников и связан с их функцией пространственной когерентности ${{\Gamma }_{{FF}}}({{x}_{1}},{{x}_{2}})$ как ${{\Gamma }_{{FF}}}({{x}_{1}},{{x}_{2}})$ ≡ ≡ $\left\langle {F({{x}_{1}})F{\text{*}}({{x}_{2}})} \right\rangle $ = ${{I}_{F}}\delta ({{x}_{1}} - {{x}_{2}}).$ Множитель $\exp ( - \alpha h)$ связан с затуханием излучения в слое, а множитель ${{\sin (kh)} \mathord{\left/ {\vphantom {{\sin (kh)} k}} \right. \kern-0em} k}$ определяет расфазировку, вызванную различием акустических путей от разных точек слоя до гидрофонов. Одновременно с корреляционной функцией можно определить средний квадрат акустического давления (пропорциональный мощности термоакустического излучения), регистрируемого фиксированным гидрофоном:

В отличие от функции когерентности (4) величина ${{P}_{{layer}}}$ монотонно растет с ростом толщины слоя и при $h \to \infty $ достигает предельного значения, равного ${{P}_{{inf}}} = {{{{I}_{F}}} \mathord{\left/ {\vphantom {{{{I}_{F}}} {(4\alpha )}}} \right. \kern-0em} {(4\alpha )}} = {{qT} \mathord{\left/ {\vphantom {{qT} 2}} \right. \kern-0em} 2},$ что с точностью до размерностного коэффициента ${q \mathord{\left/ {\vphantom {q 2}} \right. \kern-0em} 2}$ совпадает с температурой слоя.

В реальном эксперименте присутствует фоновое термоакустическое излучение (создаваемое в каждой точке как слоем, так и, например, стенками кюветы) с температурой ${{T}_{{bg}}}.$ Для учета влияния рассеянного слоем фонового поля на функцию когерентности (4), следует положить мощность источников в слое равной [11]:

Излучение стенок попадает на каждый из преобразователей с одной его стороны непосредственно, а с другой стороны – пройдя слой и ослабнув в $\exp ( - 2\alpha h)$ раз. Поэтому суммарный средний квадрат акустического давления равен

При $h \to 0$ или при $T = {{T}_{{bg}}},$ когда температура в системе постоянна, из (7) следует, что ${{P}_{{sum}}} = q{{T}_{{bg}}}.$

Для оценки чувствительности интенсиометрического и корреляционного методов ниже используется аппарат проверки статистических гипотез. Пусть в эксперименте проводится $N \gg 1$ независимых измерений акустического давления ${{p}_{i}}({{t}_{n}}),$ где $i = 1;2$ – номер гидрофона и ${{t}_{n}}$ – дискретный момент времени $n$-го измерения. Значения ${{p}_{i}}({{t}_{n}})$ можно считать независимыми, если каждый промежуток времени ${{t}_{{n + 1}}} - {{t}_{n}}$ превышает ширину автокорреляционной функции сигнала ${{\tau }_{{corr}}},$ которую, в свою очередь, можно оценить по ширине спектра $\Delta f$ регистрируемого сигнала: ${{\tau }_{{corr}}} \cong {1 \mathord{\left/ {\vphantom {1 {\Delta f}}} \right. \kern-0em} {\Delta f}}.$ Если общее время съема данных равно ${{T}_{{\text{0}}}},$ то $N \cong {{T}_{{\text{0}}}}\Delta f.$

Выдвигается нулевая гипотеза ${{H}_{0}},$ в рамках которой температура слоя $T$ полагается равной ${{T}_{{bg}}}.$ Альтернатива ${{H}_{1}}$ предполагает, что температура слоя отлична от ${{T}_{{bg}}}.$ Уровень значимости $\gamma $ (т.е. допустимая вероятность отвергнуть гипотезу ${{H}_{0}},$ когда на самом деле она верна) для определенности устанавливается равным 0.05. Под предельной чувствительностью каждого метода будет подразумеваться такое минимальное изменение температуры слоя (контраст) $\Delta T = \left| {T - {{T}_{{bg}}}} \right|,$ при котором в отсутствие помех гипотеза ${{H}_{0}}$ будет отвергнута.

При интенсиометрическом методе вычисляется средний квадрат акустического давления ${{P}_{N}} = \frac{1}{N}\sum\nolimits_{n = 1}^N {{{{\left( {\operatorname{Re} {{p}_{1}}({{t}_{n}})} \right)}}^{2}}} $ на одном из гидрофонов. Если справедлива гипотеза ${{H}_{0}},$ то величины $\operatorname{Re} {{p}_{1}}({{t}_{n}})$ имеют нормальное распределение $\operatorname{Re} {{p}_{1}}({{t}_{n}})\sim \mathcal{N}(0,\,\,q{{T}_{{bg}}})$ со средним значением 0 и дисперсией $q{{T}_{{bg}}},$ которая определяется выражением (7) при $T = {{T}_{{bg}}}.$ Тогда величина ${{{{P}_{N}}N} \mathord{\left/ {\vphantom {{{{P}_{N}}N} {(q{{T}_{{bg}}})}}} \right. \kern-0em} {(q{{T}_{{bg}}})}}$ имеет распределение ${{\chi }^{2}}$ [15]: ${{{{P}_{N}}N} \mathord{\left/ {\vphantom {{{{P}_{N}}N} {(q{{T}_{{bg}}})}}} \right. \kern-0em} {(q{{T}_{{bg}}})}}\sim {{\chi }^{2}}(N).$ С учетом того, что количество измерений в термоакустических экспериментах, как правило, велико ($N \gg 1$), можно с большой точностью заменить это распределение нормальным: ${{\chi }^{2}}(N) \to \mathcal{N}(N,2N).$ Тогда $\sqrt {\frac{N}{2}} \left( {\frac{{{{P}_{N}}}}{{q{{T}_{{bg}}}}} - 1} \right)\sim \mathcal{N}(0,1).$ Гипотеза ${{H}_{0}}$ не отвергается на уровне значимости $\gamma ,$ если

где ${{z}_{{1 - {{{\gamma }} \mathord{\left/ {\vphantom {{{\gamma }} 2}} \right. \kern-0em} 2}}}}$ – квантиль уровня $1 - {\gamma \mathord{\left/ {\vphantom {\gamma 2}} \right. \kern-0em} 2}$ стандартного нормального распределения.

При корреляционном подходе вычисляется коэффициент корреляции

Величина ${{r}_{N}}({{\tau }_{{layer}}})\sqrt {\frac{{N - 2}}{{1 - {{{\left\{ {{{r}_{N}}({{\tau }_{{layer}}})} \right\}}}^{2}}}}} $ при выполненной гипотезе ${{H}_{0}}$ имеет распределение Стьюдента [15], которое при большом $N$ стремится к стандартному нормальному распределению $\mathcal{N}(0,1).$ С учетом этого, а также с учетом того обстоятельства, что обычно коэффициент корреляции небольшой, т.е. $\left| {{{r}_{N}}({{\tau }_{{layer}}})} \right| \ll 1,$ получается ${{r}_{N}}({{\tau }_{{layer}}})\sqrt N \sim \mathcal{N}(0,1).$ Тогда гипотеза ${{H}_{0}}$ не отвергается на уровне значимости $\gamma ,$ если

Для оценки предельной чувствительности $\Delta T$ каждого метода в выражениях (8) и (9) вместо экспериментально измеряемых величин ${{P}_{N}}$ и ${{r}_{N}}({{\tau }_{{layer}}})$ нужно взять их оценки, полученные, соответственно, на основе (7) и (4) с учетом (6) при $T = {{T}_{{bg}}} + \Delta T,$ где $\Delta T \ll {{{\rm T}}_{{bg}}}{\text{:}}$

Тогда, в итоге, из выражений (8) и (9) получается оценка для чувствительности $\Delta {{T}_{P}}$ интенсиометрического метода и чувствительности $\Delta {{T}_{{corr}}}$ корреляционного метода:

Если слой толстый, т.е. $h \to \infty ,$ то из (10) следует: $\Delta {{T}_{P}} \to {{T}_{{bg}}}{{z}_{{1 - {{{\gamma }} \mathord{\left/ {\vphantom {{{\gamma }} 2}} \right. \kern-0em} 2}}}}2\sqrt {{2 \mathord{\left/ {\vphantom {2 N}} \right. \kern-0em} N}} $ и $\Delta {{T}_{{corr}}} \to \infty .$ Таким образом, описанная схема корреляционных измерений в этом случае не работает. В то же время интенсиометрический метод дает хорошие результаты. Например, для параметров $\Delta f = 200$ кГц, ${{T}_{0}} = 1$ с и ${{T}_{{bg}}} \approx 300\,\,{\text{K,}}$ которые соответствуют экспериментам, проведенным в настоящей работе, с учетом ${{z}_{{1 - {{{\gamma }} \mathord{\left/ {\vphantom {{{\gamma }} 2}} \right. \kern-0em} 2}}}} \approx 1.960$ при $\gamma = 0.05$ получается $\Delta {{T}_{P}} \approx 3.7\,\,{\text{K}}{\text{.}}$ Для тонкого слоя, когда $h \to 0,$ из (10) следует $\Delta {\kern 1pt} {{T}_{P}}\, \to \,{{T}_{{bg}}}{{z}_{{1 - {{{\gamma }} \mathord{\left/ {\vphantom {{{\gamma }} 2}} \right. \kern-0em} 2}}}}{{(\alpha h)}^{{ - 1}}}\sqrt {{2 \mathord{\left/ {\vphantom {2 N}} \right. \kern-0em} N}} $ и $\Delta {\kern 1pt} {{T}_{{corr}}}\, \to \,{{T}_{{bg}}}{{z}_{{1 - {{{\gamma }} \mathord{\left/ {\vphantom {{{\gamma }} 2}} \right. \kern-0em} 2}}}}{{(\alpha h)}^{{ - 1}}}$$\sqrt {{1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}} = {{\Delta {{T}_{P}}} \mathord{\left/ {\vphantom {{\Delta {{T}_{P}}} {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}.$ Это означает, что корреляционный метод в этом случае более предпочтителен. Такое преимущество корреляционного метода, возникающее при рассмотрении объектов малого размера, можно усилить применением предварительной фокусировки полей [12, 14]. В общем случае, в многоканальных корреляционных системах акустической термотомографии роль толщины $h$ играет характерный размер элемента разрешения [14]. Для слоя резины, который был использован в корреляционных экспериментах в представляемой работе (см. ниже; $\alpha = 250\,\,{{{\text{м}}}^{{ - 1}}}$ и $h = 0.45$ мм), из (10) получается $\Delta {{T}_{{corr}}} = 26\,\,{\text{K}}$ и $\Delta {{T}_{P}} = 18\,\,{\text{K,}}$ т.е. чувствительность корреляционного метода немного хуже, чем интенсиометрического.

Следует отметить, что сделанные оценки исходят из предположения отсутствия дополнительных помех, например, электрических шумов усилителей. Наличие таких шумов ухудшает чувствительность устройства.

РЕГИСТРАЦИЯ ТЕРМОАКУСТИЧЕСКОГО СИГНАЛА

Приемные гидрофоны обладали чувствительностью ${{K}_{{hyd}}},$ которая достигала максимума $ \approx {\kern 1pt} 35\,\,{\text{мкВ}} \cdot {\text{П}}{{{\text{а}}}^{{ - 1}}}$ на центральной частоте ${{f}_{0}} = 1$ МГц. Их полоса пропускания составляла $\Delta f \approx 200$ кГц. Сигналы с них усиливались и оцифровывались, после чего к каждому из них последовательно применялись прямоугольный фильтр с полосой частот 0.5–1.2 МГц и фильтр винеровского типа, способ построения частотной характеристики которого обсуждается ниже.

После применения прямоугольного фильтра сигнал включал в себя как широкополосную акустическую часть, так и широкополосную наводку. Для их разделения проводился следующий эксперимент. Два гидрофона, направленные друг на друга, находились в кювете, заполненной водой. Присутствующее в среде акустическое излучение формировало в выборочной функции взаимной когерентности выходных сигналов $W(\tau )$ максимумы при временных задержках ${{\tau }_{ \pm }} = \pm {l \mathord{\left/ {\vphantom {l {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}},$ где $l = \left| {{{l}_{1}} - {{l}_{2}}} \right|$ – расстояние между гидрофонами. Физические аспекты возникновения этих максимумов обсуждались в [16]. Максимум при времени задержки ${{\tau }_{0}} = 0$ соответствует электромагнитным помехам, которые приходят на оба гидрофона одновременно. Тогда, используя тот факт, что максимумы при временных задержках ${{\tau }_{ \pm }}$ соответствуют принятым акустическим сигналам, можно оценить их спектры мощности и построить фильтр винеровского типа для максимального подавления помех неакустической природы. С этой целью вводится оконная функция

где ${{\tau }_{{corr}}} \cong {1 \mathord{\left/ {\vphantom {1 {\Delta f}}} \right. \kern-0em} {\Delta f}}$ – ширина корреляционного пика, соответствующая максимуму $W(\tau ).$ С помощью функции $g(\tau )$ можно выделить часть выборочной функции когерентности ${{W}_{{sig}}}(\tau ) = W(\tau )g(\tau ),$ которую формируют в основном акустические сигналы, и часть ${{W}_{{interf}}}(\tau ) = W(\tau )\left[ {1 - g(\tau )} \right],$ которая соответствует помехе. Тогда, применяя преобразование Фурье к этим двум частям функции когерентности, с использованием теоремы Винера–Хинчина можно определить спектры мощности акустических сигналов ${{\tilde {W}}_{{sig}}}(\omega )$ и помехи ${{\tilde {W}}_{{interf}}}(\omega ),$ соответственно. Это позволяет построить фильтр винеровского типа с характеристикой $\Omega (\omega ) = {{{{{\tilde {W}}}_{{sig}}}(\omega )} \mathord{\left/ {\vphantom {{{{{\tilde {W}}}_{{sig}}}(\omega )} {\left[ {{{{\tilde {W}}}_{{sig}}}(\omega ) + {{{\tilde {W}}}_{{interf}}}(\omega )} \right]}}} \right. 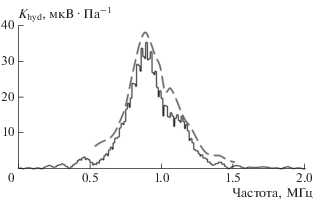\kern-0em} {\left[ {{{{\tilde {W}}}_{{sig}}}(\omega ) + {{{\tilde {W}}}_{{interf}}}(\omega )} \right]}}.$

Применение такого фильтра существенно уменьшает влияние помех. Например, в проведенных экспериментах отмечалось уменьшение амплитуды центрального корреляционного максимума $W({{\tau }_{0}})$ примерно на порядок. Следует обратить внимание на два обстоятельства. Во-первых, процедура построения описанного фильтра не требует априорной информации о системе, т.е. она универсальна. Во-вторых, так как и термоакустическое излучение в рабочей полосе частот, и помеха близки по свойствам к белому шуму, то характеристика фильтра $\Omega (\omega )$ пропорциональна АЧХ приемной системы. Однако при этом построенный фильтр $\Omega (\omega )$ не несет информации об абсолютной чувствительности приемного устройства. На рис. 1 характеристика $\Omega (\omega ),$ умноженная на максимальное значение чувствительности гидрофонов ${{K}_{{hyd}}},$ представлена вместе с данными взаимной градуировки двух гидрофонов. Видно, что кривые совпадают с большой точностью. Это дает возможность в будущем использовать термоакустическое излучение для проведения таких градуировок, если другие способы оказываются по какой-то причине сложнее.

ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ ИНТЕНСИОМЕТРИЧЕСКИМ И КОРРЕЛЯЦИОННЫМ МЕТОДАМИ

В ходе интенсиометрического эксперимента единственный приемный гидрофон располагался в кювете с водой комнатной температуры. Слой резины с большой толщиной $h = 4$ см устанавливался в акустически прозрачный стакан и размещался рядом с гидрофоном. В стакан наливался кипяток, благодаря чему мощность регистрируемого термоакустического излучения возрастала. Для независимого контроля температура воды в стакане, совпадающая с температурой поверхности слоя, измерялась термопарой.

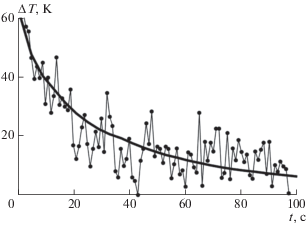
Приращение мощности сигнала, вызванное нагревом резины, достигало 2% и, в соответствии с предварительной градуировкой, пересчитывалось в температурный контраст $\Delta T = \left| {T - {{T}_{0}}} \right|.$ В течение эксперимента температура воды в стакане и, следовательно, температура резины уменьшалась, что приводило к постепенному уменьшению мощности сигнала. При этом температура воды в кювете практически не изменялась. Измерения температурного контраста $\Delta T$ интенсиометрически и с помощью термопары (рис. 2) согласуются между собой и имеют вид убывающей экспоненты, что соответствует процессу остывания. Хорошее совпадение позволяет говорить о возможности динамического измерения температуры интенсиометрическим методом. Следует отметить, что подобные эксперименты ранее проводились и другими группами исследователей [5, 6].

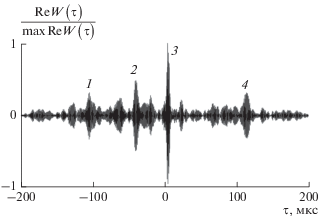
Корреляционные эксперименты проводились с участием двух гидрофонов. В первом эксперименте между гидрофонами устанавливался слой поглощающей резины толщиной $h = 0.45$ мм (что составляет около одной трети характерной длины волны), нагретый на $\Delta T = 60\,\,{\text{K}}{\text{.}}$ Рабочие поверхности гидрофонов находились в точках с координатами ${{l}_{1}} = - 10$ см и ${{l}_{2}} = 5$ см. Действительная часть выборочной функции взаимной когерентности сигналов, измеренных в этом эксперименте (общее время накопления составляло ${{T}_{{\text{0}}}} = 50$ с), приведена на рис. 3. На ней можно выделить четыре максимума, обозначенных цифрами. Максимум 2 при временной задержке ${{\tau }_{{layer}}} = {{{{({{l}_{1}} + {{l}_{2}})} \mathord{\left/ {\vphantom {{({{l}_{1}} + {{l}_{2}})} с}} \right. \kern-0em} с}}_{0}} = $ = ‒36 мкс вызван термоакустическим излучением от нагретого объекта. Максимумы 1 и 4 соответствуют суммарной временной задержке ${{\tau }_{ \pm }} = \pm {l \mathord{\left/ {\vphantom {l {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}} = \pm {{10}^{{ - 4}}}$ с [16]. Если повернуть гидрофоны на небольшой угол, т.е. сделать их не строго параллельными, величину этих максимумов удается существенно снизить. Максимум 3 при ${{\tau }_{0}} = 0$ соответствует электромагнитной наводке, приходящей на оба гидрофона синфазно.

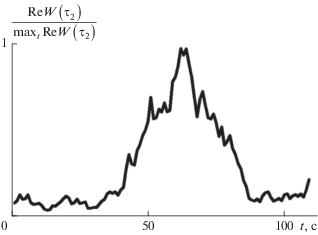
Для анализа динамики изменения температуры объекта был проведен второй эксперимент. Положение гидрофонов при этом не менялось, а слой резины, нагретый на $\Delta T = 60\,\,{\text{K,}}$ помещался между ними в момент времени ${{t}_{0}} = 50$ с после начала измерений. В отличие от предыдущего эксперимента, температура слоя не поддерживалась постоянной, и с течением времени он остывал до комнатной температуры. Общее время регистрации сигналов составило 145 с. Корреляционная обработка записанных данных велась с помощью скользящего временного окна шириной $\Delta t = 25$ с. При этом для каждого момента времени $t$ в пределах 0–120 с строились временные интервалы $[t{\text{;}}\,\,t + {{\Delta }}t],$ на которых осуществлялось вычисление и последующее усреднение выборочных функций взаимной когерентности. На графике (рис. 4) изображена зависимость амплитуды максимума 2, соответствующего временной задержке ${{\tau }_{{layer}}},$ от начала временного интервала $t,$ нормированная на свое максимальное значение. Из-за примененного скользящего окна рост этого максимума начинается не в момент $t = {{t}_{0}},$ а раньше, при $t = {{t}_{0}} - \Delta t.$ Наибольшее его значение достигается при $t = 60$ с. С течением времени величина максимума уменьшается, что соответствует охлаждению объекта. Таким образом, экспериментально показана возможность отслеживать динамику температуры модельного объекта методом корреляционной акустотермометрии.

ЗАКЛЮЧЕНИЕ

Таким образом, продемонстрирована возможность оценки температуры модельного объекта интенсиометрическим и корреляционным методами как в стационарном случае, так и в виде функции времени. Предложен способ определения относительной АЧХ системы из двух гидрофонов с помощью регистрируемого ими термоакустического излучения. Выполнены теоретические оценки предельной чувствительности по температуре каждого из методов для слоев разной толщины. Интенсиометрический метод обладает лучшей чувствительностью, если слой имеет большую толщину, в отличие от случая тонкого слоя, для которого чувствительность корреляционного метода выше. Это является следствием более высокой пространственной разрешающей способности корреляционного метода. Если использовать этот метод в сочетании с фокусировкой [13, 17], можно ожидать сохранения данного преимущества с одновременным ростом чувствительности по температуре.

Исследование выполнено при финансовой поддержке РФФИ и Правительства Москвы (проект № 21-32-70003).